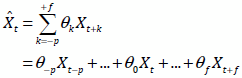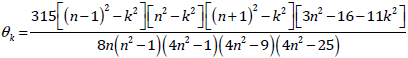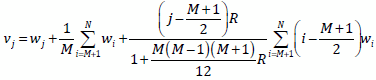Main article
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
1 Introduction
Understanding how the amount of water yield 1 has changed in Canada is an integral part of Statistics Canada's Water Accounts. The framework for these accounts, the Canadian System of Environmental and Resource Accounts (CSERA), establishes an outline for estimates of stocks and flows of water moving within and between the natural environment and society. The framework offers an integrated view of water and its use by society through the compilation of environmental data that are consistent over space and time, national in coverage and compatible with economic accounts. An important part of the water accounting program is the measurement and analysis of these stocks and flows as they change over time. This is in keeping with one of Statistics Canada's objectives: the identification, measurement and tracking of trends in order to facilitate public debate and decision-making. This paper describes the trend estimation methodology used in the 2010 issue of Human Activity and the Environment: Freshwater supply and demand in Canada (Statistics Canada, 2010).
The search for trends in hydrometeorological data has become a regular undertaking given the ever-increasing need to understand how the magnitudes of present and historical components of the hydrological cycle evolve over time. Numerous studies have been conducted which use nonparametric rank-based techniques to determine the magnitude and significance of a trend found between time and streamflow. The Mann-Kendall test (Salmi et al., 2002), one of the main methods used for trend estimation, provides a global robust estimate of the slope of the underlying trend in the series of annual water yield estimates. In this paper we present a methodology to complement this global estimate where the time series is deconstructed into several components separating the underlying trend-cycle from the irregularities in the series. To achieve this objective we first estimate a trend plus the cyclical component for the series of water yield estimates. We then describe the global trend over the span of the series by fitting a linear model to the trend-cycle estimate. To demonstrate this methodology, we used a water yield series from 1971 to 2004 for Southern Canada.
2 Data and methods
The water yield data consist of spatial estimates of average monthly unregulated flow (km3) summarized annually across Canada from 1971 to 2004. These water yield estimates were produced by means of a geostatistical approach that in short involved kriging regionalized unregulated flow per unit area (km3/km2). After interpolation the km3/km2 estimates were converted back into km3 for the desired accounting units. The unregulated flow data were obtained from the Water Survey of Canada's hydrometric database HYDAT (Environment Canada, 2007). A detailed description of the methodology used to derive the water yield estimates can be found in Bemrose et al. (2009). Given the paucity of data, especially in the North, this study evaluated the changes in water yield for the area of 2,598,632 km2 below the North-line 2 (Map 1). The series of annual estimates of water yield below the North-line can be seen in Chart 1.
A time series often consists of four components: the trend component which represents the systematic long-term movement over the span of the series; the cycle which describes the smooth movement around the trend; the seasonal component which consists of intra-year fluctuations, either monthly or quarterly; and the irregular (noise) component which is the residual not accounted for by the other components (Ladiray and Quenneville, 2001). Since the input series of water yield consisted of annual values, the seasonal component is not a component in the series. Consequently, the values were influenced only by the long-term trend, the quasi-cyclical fluctuations (the long-term trend and the quasi-cyclical fluctuations together are referred to as the signal), and the irregular component (that is, the difference or ratio between the signal and the observations).
To estimate the signal, we used a nonparametric approach, whereby the series
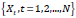 was
smoothed by a moving average of coefficients as follows:
was
smoothed by a moving average of coefficients as follows:
where
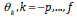 are the weights and
are the weights and
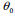 is the central weight for the moving averages
from
is the central weight for the moving averages
from
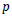 the "past" and
the "past" and
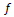 "future" observations (Dagum, 1985;
Ladiray and Quenneville, 2001). The resulting smoothed series is termed
the trend-cycle because it consists of the long-term trend and cyclical fluctuations.
The number of terms in the moving average is
"future" observations (Dagum, 1985;
Ladiray and Quenneville, 2001). The resulting smoothed series is termed
the trend-cycle because it consists of the long-term trend and cyclical fluctuations.
The number of terms in the moving average is
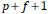 . When
. When
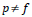 the filter is asymmetric; when
the filter is asymmetric; when
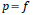 , and
, and
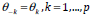 the
filter is symmetric.
the
filter is symmetric.
In this study, we used the Henderson (1916) filter to estimate the trend-cycle
wherever there were enough observations to satisfy the
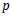 and
and
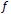 requirements. The Henderson filter reproduces
local polynomials up to order 3. With a 17-term Henderson filter
we estimated the trend-cycle locally using 8 observations in the
past and 8 observations in the future. To derive the 17 weights
for the filter using Equation (2), we substituted 8 for
requirements. The Henderson filter reproduces
local polynomials up to order 3. With a 17-term Henderson filter
we estimated the trend-cycle locally using 8 observations in the
past and 8 observations in the future. To derive the 17 weights
for the filter using Equation (2), we substituted 8 for
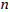 and
the values were obtained for each
and
the values were obtained for each
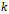 from -8 to 8 (Dagum et al., 1996;
Ladiray and Quenneville, 2001). The symmetric weights for the 17-term
Henderson filter can be seen in Figure 1.
from -8 to 8 (Dagum et al., 1996;
Ladiray and Quenneville, 2001). The symmetric weights for the 17-term
Henderson filter can be seen in Figure 1.
Given the end-point problem with the Henderson symmetric filter, we used
an asymmetric approach developed by Musgrave (1964) to determine the
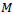 coefficients
coefficients
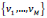 using
the symmetric
using
the symmetric
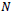 coefficients
coefficients
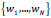 wherever
wherever
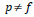 . Using the formula presented in Doherty (2001)
and Findley et al. (1998) we calculated the Musgrave weights as follows:
. Using the formula presented in Doherty (2001)
and Findley et al. (1998) we calculated the Musgrave weights as follows:
where
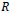 was set to 4.5 for the 17-term Henderson
filter. For a more detailed description of the Henderson filter and the associated
Musgrave filter, see Ladiray and Quenneville (2001). The surrogate asymmetric
coefficients used for the 17-term Henderson filter are presented in Figure 1. The coefficients for each
was set to 4.5 for the 17-term Henderson
filter. For a more detailed description of the Henderson filter and the associated
Musgrave filter, see Ladiray and Quenneville (2001). The surrogate asymmetric
coefficients used for the 17-term Henderson filter are presented in Figure 1. The coefficients for each
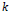 from -8 to 8 sum to 1 for
the Henderson filter when symmetric and asymmetric.
from -8 to 8 sum to 1 for
the Henderson filter when symmetric and asymmetric.
Figure 1: Coefficients for the symmetric and asymmetric 17-term Henderson filter
The 17-term filter was selected for this series and for those presented in the Statistics (2010) publication on the basis of its gain function displayed in Chart 2.
The gain function shows the frequencies eliminated or preserved by the moving average (Ladiray and Quenneville, 2001). From Chart 2, it can be seen that the filter preserves 99% of the strength of cycles that repeat once every 34 years and 89% of those that repeat twice over 34 years; this is followed by a further decrease until all cycles that repeat more than five times are eliminated. For details on how the gain function is calculated, see Dagum et al. (1996) or Ladiray and Quenneville (2001).
The Henderson filter is available in seasonal adjustment software such as the U.S. Bureau of Census X11 (Shiskin et al., 1967) and its variants including the X11-ARIMA (Dagum, 1988) and X12-ARIMA (Findley et al., 1998). We implemented the latter X12-ARIMA in this study using the trend option. The software works through an iterative process where in the first stage it evaluates the trend-cycle for the original series (Chart 3) and determines the adjustment factors for the extreme values in the irregular component (Chart 4). In the second stage of processing the original series is modified for the extreme values, and the trend-cycle is recalculated (Chart 5); again, adjustment factors are determined for the extreme values in the irregular component (Chart 6). In the final stage of the processing chain, the original series is further modified for the extreme values and the final trend-cycle is recalculated (Chart 7). An overlay of the trend-cycles estimated through each stage of processing can be seen in Chart 8.
Local estimation of the trend-cycle and local down-weighting of extreme values is illustrated in charts 6 and 7. Although the low water yield for 1978 is comparable to the levels observed in 1985, 1987, 1989, 1998, 2000, and 2001, it is considered atypical in comparison to its local neighbours. After producing the local trend-cycle for the series, we fitted a linear trend to the trend-cycle using the minimum least squares method to describe the global trend over the span of the series. 3
3 Results
Chart 9 displays the trend-cycle produced using the iterative process along with the linear fit to the trend-cycle, which describes the global trend. The intercept is estimated at 1,388 km3, and the slope is -3.52 km3/yr.
The trend-cycle locally decreased from 1971 to 1987, increased until 1995, and then decreased again until 2004. Nineteen seventy-eight was the first year identified with an atypical water yield, but similar values have been observed in years since.
4 Conclusion
Water yield for the area below the North-line has globally decreased at a rate of 3.52 km3/yr from 1971 to 2004. Given that this is an aggregation of observations over a large and varied geographic area it is important to recognize that some regions may actually have had increasing water yields over the last 34 years, while the area as a whole experienced a decrease.
It is difficult to compare these results to those of other studies, given that most other studies focus on detecting changes that occur at localized areas over differing record lengths. However, some studies have made conclusions regarding the general trend for regions on the basis of an aggregation of clustered observations over fairly similar time periods. Zhang et al. (2001) found that annual average streamflow was for the most part decreasing across southern Canada from 1967-1996. This finding is similar to that presented in Rivard et al. (2009), who evaluated trends in groundwater recharge. They found that groundwater recharge has generally decreased for all observations below 55º latitude especially for Atlantic Canada from 1970 to 1997.
- Date modified: