Méthodologie de l'indice de volume en chaîne Fisher

Consulter la version la plus récente.

Version imprimable (PDF) de cet article

Le 31 mai 2001, les comptes trimestriels des revenus et dépenses ont adopté la formule de l’indice de Fisher, enchaîné trimestriellement, comme mesure officielle du produit intérieur brut réel en termes de dépenses. Cette formule a également été adoptée pour les comptes provinciaux le 31 octobre 2002. 

Deux raisons ont motivé l’adoption de cette formule : fournir aux utilisateurs une mesure plus précise de la croissance du PIB réel entre deux périodes consécutives, et rendre comparable la mesure canadienne aux comptes des revenus et des produits des États-Unis, qui utilisent la formule de l’indice de Fisher en chaîne depuis 1996 pour mesurer le PIB réel. 

Les pages suivantes exposent la théorie ainsi que l’application de la formule aux comptes économiques canadiens.

Table des matières :

• Introduction
• Construction d'un indice et enchaînement

• Exemple 1: Une économie de vins et fromages....
• Exemple 2: La production de vins et fromages sans l'effet prix...
• Exemple 3: Une autre façon d'enlever l'effet prix

Choix de l'indice

• Dans les années 90, la haute technologie bouleverse la structure des prix...

Application aux comptes des revenus et dépenses

• Transformation des indices de volume
• Exemple 4: Dans la pratique: la méthode de déflation.

Les comptes économiques et financiers nationaux trimestriels et annuels

• Niveau de détail à l'échelle nationale

Le problème des inventaires

Les comptes provinciaux et le PIB réel

• Niveau de détail à l'échelle provinciale
• Sources de biais entre les systèmes national et provincial

Le problème de la non-additivité

• Formule de contribution au pourcentage
• La contribution d'une série à la croissance du PIB

Questions et réponses

• Lectures suggérées

Introduction

La croissance du produit intérieur brut (PIB) ou de tout autre agrégat en valeur nominale peut être décomposée en deux éléments : un « effet prix », soit la part de la croissance reliée à l’inflation, et un « effet volume », qui recoupe la variation des quantités, de la qualité et de la composition de l’agrégat. L’effet volume est présenté dans les Comptes nationaux par ce que l’on appelle les séries « réelles » (comme le PIB réel).

Dans les Comptes nationaux canadiens, l’effet volume est évalué par la méthode de déflation. Cette méthode consiste à enlever l’effet prix de chaque composante faisant partie de l’agrégat, puis à agréger les composantes ainsi déflatées pour obtenir un effet volume « total ».

Il existe plusieurs façons d’agréger les composantes d’un tout dont on veut calculer l’effet volume. La théorie des indices offre une panoplie d’outils à cet effet. L’approche privilégiée par Statistique Canada depuis le printemps 2001 est celle de l’indice en chaîne de Fisher. Cette mesure est théoriquement supérieure à l’ancienne mesure Laspeyres à base fixe, en plus de rendre les données canadiennes comparables aux mesures officielles de l’activité économique des États-Unis. De plus, elle permet d’être conforme aux recommandations du Système de comptabilité nationale 1993¹ (SCN 1993).

Les paragraphes suivants expliquent, de manière simplifiée, les méthodes dorénavant utilisées par les Comptes nationaux pour mesurer l’activité économique réelle du pays

Construction d'un indice et enchaînement

Un agrégat donné (PIB ou autre) en valeur nominale représente une sommation de quantités évaluées dans une même unité monétaire, aux prix de la période courante. Pour prendre l’exemple du PIB, cette sommation peut s’exprimer par PIB = Σpq , soit la somme de toutes les quantités de biens et services transigés dans l’économie, multipliées par leurs prix respectifs. La variation du PIB nominal, entre une période o et une période t, peut donc être exprimée, sous forme indicielle², par:

(1)
où:	ΔPIBt/o est l'indice de valeur du PIB pt est le prix au temps t po est le prix au temps o qt est la quantité au temps t qo est la quantité au temps o

Exemple 1: Une économie de vins et fromages...

La variation donnée par cette formule peut théoriquement être divisée en une variation des prix et une variation des quantités. S’il existait un « prix moyen » du PIB, on pourrait tout simplement diviser la variation du PIB (donnée par l’équation (1)) par ce prix moyen pour obtenir la variation moyenne des quantités. La plupart du temps dans les comptes nationaux, un tel prix moyen n’existe pas. La variation totale des quantités ne peut donc être calculée qu’en faisant la somme des variations de quantités dans l’économie.

Or, faire une telle somme est problématique du fait que l’on ne peut additionner des quantités dont les unités sont physiquement différentes, comme par exemple des voitures et des téléphones, voire deux différents modèles de voiture. Les quantités doivent donc être réévaluées selon une unité commune. Dans une économie monétisée, le plus simple est d’exprimer les quantités en termes monétaires : une fois évaluées, c’est-à-dire multipliées par des prix, les quantités peuvent être aisément agrégées.

Une forme intuitive de mesurer les variations de quantité à travers le temps est de prendre les prix disponibles à une période donnée et de multiplier les quantités des périodes subséquentes par ces mêmes prix. Il s’agit en fait de réévaluer les quantités courantes à des prix fixes dans le temps, ce qui a pour effet d’ « enlever » l’effet prix. En termes mathématiques, on retrouve ainsi la formule de l’indice de Laspeyres à base fixe :

(2)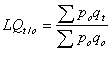
où:	LQt/o est l'indice de quantité de Laspeyres po est le prix au temps o qt est la quantité au temps t qo est la quantité au temps o

L’unique différence d’avec l’équation (1) se trouve au numérateur, où les quantités au temps t sont multipliées cette fois par les prix du temps o.

Exemple 2: La production de vins et fromages sans l'effet prix...

Il est évident qu’avec une telle formulation, les résultats dépendent fortement de la structure des prix au moment o. S’il s’avère que cette structure change avec le temps, par exemple par suite de la chute du prix d’une composante comparativement aux autres, l’indice de l’équation (2) devient éventuellement biaisé du fait qu’il dépend alors d’une structure de prix devenue désuète.

Une façon de contourner ce genre de problème est de mettre à jour périodiquement la base de pondération de manière à la rapprocher de la période courante. Cette technique a été utilisée par le passé dans le Système des comptes nationaux (SCN), alors que les séries réelles étaient rebasées à tous les cinq ou six ans afin de refléter les changements dans la structure des prix.

Il peut arriver toutefois que la structure des prix se mette à changer plus rapidement qu’à l’habitude. La base de pondération devient alors rapidement désuète, au point où il peut devenir nécessaire d’accélérer la fréquence du rebasement. Ultimement, la base de pondération peut être déplacée systématiquement de période en période, de sorte qu’elle soit définie comme étant la période précédant la période courante :

(3)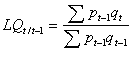

où l’on retrouve, en place du p_o de l’équation (2), p_t-1. Cet indice « à base mobile » donne, pour la période courante t, la croissance du volume pondérée selon les prix de t-1. Il intègre, en quelque sorte, la fréquence du rebasement, ce qui élimine le côté arbitraire d’un rebasement effectué seulement au besoin.

Ce genre d’indice, à l’horizon court, peut être adapté de manière à ce qu’il couvre plusieurs périodes. Les variations entre périodes successives (telles que calculées par l’équation (3)) peuvent être cumulées, c’est-à-dire multipliées entre elles à la manière d’un calcul d’intérêt composé. C’est de cette façon qu’est effectué l’enchaînement d’un indice. Dans la chaîne ainsi formée, les prix utilisés pour la pondération sont des prix très récents et ne deviennent jamais obsolètes. Selon notre exemple, un indice chaîné prendrait la forme suivante :

(4)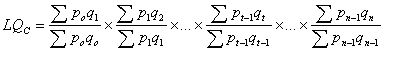
où:	n est le nombre de périodes sur lesquelles s'étend l'indice en chaîne

Exemple 3: Une autre façon d'enlever l'effet prix

Le Système de comptabilité nationale (1993) recommande l’utilisation d’indices en chaîne. Cette recommandation est suivie par Statistique Canada depuis le printemps 2001 pour les Comptes économiques et financiers nationaux trimestriels et depuis l’automne 2002 pour les Comptes économiques provinciaux ainsi que pour le PIB par industrie. L’enchaînement systématique permet un renouvellement continuel de la base de pondération, évitant ainsi le problème de désuétude qui accompagne l’utilisation d’un indice à base fixe.

Choix de l'indice

Les exemples ci-dessus réfèrent à un indice de type Laspeyres. La théorie des indices fournit toutefois de nombreux autres indices, qui diffèrent dans la façon dont sont pondérées les composantes. Par exemple, alors que les quantités de l’indice de Laspeyres sont pondérées avec les prix d’une période précédente, elles sont pondérées dans l’indice de Paasche avec les prix de la période courante :

(5)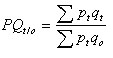
où:	PQt/o est l'indice de quantité de Paasche

Cet indice est en fait la réciproque de l’indice de Laspeyres. Utilisé dans sa forme à base fixe, il présente le même problème que celui décrit plus haut, mais à l’inverse : il ne reflète pas adéquatement les changements de structure de l’économie pour les périodes antérieures. Toutefois, l’indice de Paasche peut être enchaîné de la même manière que l’indice de Laspeyres (comme dans l’équation (4)).

Il peut être démontré qu’en général, un indice de quantité de Laspeyres fera apparaître une augmentation dans le temps plus importante qu’un indice de quantité de Paasche. Cela se produit lorsque les prix et les quantités sont négativement corrélés, c’est-à-dire lorsque des biens ou des services devenus relativement plus coûteux sont remplacés par des biens et services devenus relativement moins coûteux. Cet effet de substitution, couramment observé, fait dire à la théorie économique que les indices de Laspeyres et de Paasche fixent les limites supérieures et inférieures d’un indice théorique idéal, moins biaisé.

Cet indice théorique peut être approché par un indice de type Fisher, qui représente la moyenne géométrique d’un indice de Laspeyres et de Paasche :

(6)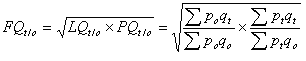
où:	FQt/o est l'indice de quantité de Fisher

En plus de sa supériorité théorique, cet indice comporte quelques propriétés souhaitables dans le cadre de la comptabilité nationale. Par exemple, il est « réversible dans le temps », c’est-à-dire que l’indice montrant la variation entre la période o et la période t est la réciproque de l’indice montrant la variation entre la période t et la période o. Une autre caractéristique intéressante est la « réversibilité des facteurs », en vertu de laquelle le produit des indices de prix et de quantité est égal à l’indice de variation des valeurs courantes :

Nous retrouvons notre indice de variation nominale de l’équation (1) et la décomposition « effet prix » et « effet quantité » évoquée au début de ce texte. Il devient dès lors aisé de trouver le prix implicite Fisher du PIB en divisant le PIB en dollars courant par le PIB réel selon la formule Fisher. Les indices de Laspeyres et de Paasche ne présentent aucune de ces deux propriétés.

Statistique Canada utilise la formule de l’indice Fisher en chaîne comme mesure du PIB réel. Une fois enchaînée à la manière de l'équation (4), l'équation (6) devient :

(7)

C’est la formule qui sert de base aux calculs du PIB réel des comptes nationaux et provinciaux.

Dans les années 90, la haute technologie bouleverse la structure des prix....

Application aux comptes des revenus et dépenses

Dans la pratique, les formules exposées ci-dessus ne peuvent être utilisées telles quelles par les Comptes des revenus et dépenses, vu l’absence de données sur les quantités et sur les niveaux de prix. Seules les séries en valeur courante (C) et des indices de prix (donc les prix relatifs) sont disponibles. Les formules doivent être transformées en utilisant le fait que le prix multiplié par la quantité (p_tq_t) équivaut à la série en dollars courants (C_t). On obtient alors des formules exprimées en termes de séries nominales (C_t) et de prix relatifs (p_t/p_t-1 ou l'inverse). De cette façon, le Laspeyres s'écrit (à partir de l'équation (3)) :

(8)

. pour le Paasche (à partir de l'équation (5)):

(9)

. et enfin, pour le Fisher (moyenne géométrique des équations (8) et (9)):

(10)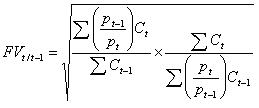

C’est cette formule, chaînée, qui est utilisée dans la pratique. Le détail des transformations peut être examiné ici.

Les séries n’étant plus exprimées ici en termes de quantités, on parlera alors d’indice de volume. La notion de volume est plus large que celle de quantité, puisqu’elle comprend les variations de qualité et, ultimement, les changements dans la composition de l’économie.

Exemple 4: Dans la pratique: la méthode de déflation

Les comptes économiques et financiers nationaux trimestriels et annuels

Les agrégats réels publiés par la Division des comptes des revenus et dépenses sont déterminés à l’aide de l’équation (10) vue ci-dessus. Pour chaque agrégat réel, un indice est calculé à partir des séries composantes, puis chaîné d’un trimestre à l’autre à la manière présentée dans les exemples 3 et 4. La série d’indices chaînés ainsi obtenue est par la suite étalonnée sur une année de référence de manière à l’exprimer en dollars. L’étalonnage consiste mettre la série d’indices chaînés à un niveau tel que, pour une année de référence donnée, elle soit égale à la série de l’agrégat correspondant en dollars courants, et ce tout en maintenant les taux de croissance intacts d’un trimestre à l’autre.

Le niveau de détail - ou le nombre de composantes qui entre dans chacun des agrégats - est déterminé par la disponibilité des données et par certains déterminants de la qualité générale (comme par exemple la stabilité de la saisonnalité). Au niveau national, 435 séries en dollars courants et le même nombre de séries de prix correspondants entrent dans le calcul du PIB réel selon l'indice en chaîne Fisher. Le tableau niveau de détail à l'échelle nationale montre comment ces séries sont réparties entre les divers agrégats présentés dans le Tableau 3 de la publication Comptes nationaux des revenus et dépenses, estimations trimestrielles (13-001).

Aucun calcul de l’indice Fisher n’est effectué sur une base annuelle. Les agrégats réels annuels sont les moyennes simples des quatre trimestres de l’année. Ce sont là les mesures officielles du PIB national réel annuel.

Le problème des inventaires

Pour la plupart des postes du Tableau 3 et des autres tableaux en termes réels de la publication Comptes nationaux des revenus et dépenses, estimations trimestrielles (13-001), le calcul du Fisher ne pose pas vraiment de problèmes techniques. Il en va autrement des séries de l’investissement en stocks, qui sont des séries de premières différences. Comme ces séries fluctuent autour de zéro, il arrive que les indices Laspeyres et Paasche prennent des signes opposés; le Fisher étant une moyenne géométrique de ces deux indices, il devient indéterminé.

Les séries réelles de l’investissement en stocks publiées par la DCRD ne sont pas le résultat de calculs directs de l’indice Fisher en chaîne tels que présentés ci-dessus, mais plutôt une approximation. L’approche utilisée par la DCRD se base sur le fait qu’un investissement en stocks représente en fait la variation d’un stock total, qui lui est toujours positif. En principe, un indice Fisher peut donc être calculé sur les séries de stocks total. Une fois cet indice étalonné sur la valeur en dollars d’une période de référence, on peut supposer que les premières différences de cette série en dollars représentent une approximation de la série réelle de l’investissement en stocks.

Si une telle méthode est aisément applicable au seul calcul des inventaires réels, elle est toutefois inutilisable comme tel dans cadre du calcul du PIB réel. En effet, le calcul du PIB réel doit se faire avec des séries d’investissement en stock, et non avec des séries de stock total. Pour contourner ce problème, la DCRD utilise deux séries de stocks total plutôt qu’une pour chaque série d’investissement en stocks : une première série, au signe positif, du stock total à la période courante, et seconde série, au signe négatif, du stock total à la période précédente. Cette dernière série est en fait une série de stock total déphasée d’une période. En tout temps t, la différence entre ces deux séries correspond à l’investissement en stock au cours de cette même période. En remplaçant dans le PIB chaque série d’investissement en stock par ces deux séries de stocks total, l’une positive et l’autre négative et déphasée, on peut alors calculer le PIB réel à l’aide de la formule de l’indice en chaîne Fisher. Les prix des séries de stocks total sont ceux de l’investissement en stocks.

Le calcul des séries réelles de l’investissement en stock fait appel aux mêmes séries de stock total. Pour chaque agrégat d’investissement en stocks, un indice en chaîne Fisher est obtenu des séries du stock total à la période courante et un autre des séries du stock total déphasé. Une fois étalonnées à la période de référence, ces séries Fisher de stock total peuvent être soustraites l’une de l’autre pour simuler une série réelle Fisher de l’investissement en stocks. C’est de cette façon que sont calculés les agrégats réels de l’investissement des entreprises en stocks publiés par la Division des comptes des revenus et dépenses.

Cette méthodologie de calcul de l’investissement en stocks explique le fait que, au niveau national, on voit 110 séries de stocks impliquées dans le calcul du Fisher, dont 76 non agricoles et 34 agricoles (alors qu’en fait, on compte 55 séries d’inventaires publiées en dollars courants, dont 38 non agricoles et 17 agricoles).

Application au niveau provincial

À l'échelle provinciale, les calculs des données réelles sont effectués de la même façon qu'au niveau national, à la différence près qu'ils sont faits sur une base annuelle. L'investissement en stocks est calculé selon la méthode décrite ci-dessus, sur une base annuelle, avec des prix moyens pour l'année.

Le niveau de détail des comptes provinciaux diffère de celui des comptes nationaux trimestriels. Pour chaque province, 502 séries entrent dans le calcul du PIB réel. Le tableau niveau de détail à l'échelle provinciale montre la répartition de ces séries à travers les postes du Tableau 3 de la publication Comptes économiques provinciaux (13-213). On notera que cette répartition diffère quelque peu de la structure nationale, en raison de la disponibilité et de la qualité différentes des données provinciales.

Sources de biais entre les systèmes national et provincial

Le problème de la non-additivité

Les séries Fisher en chaîne publiées par les Comptes des revenus et dépenses ne sont pas additives, et ce problème s'accroît à mesure que l'on s'éloigne de la période de référence. La non-additivité des séries réelles provient à la fois de l’enchaînement, qui a pour effet de détruire la cohérence additive des équations comptables, et de la formule de Fisher elle-même, qui n’est pas dotée de la propriété d’additivité contrairement à la formule de Laspeyres.

Le fait que les séries réelles des Comptes n’ont plus de cohérence additive rend leur manipulation plus complexe qu’elle ne l’était à l’époque où les calculs était basés sur un indice de Laspeyres à base fixe. Par exemple, il devient difficile de mesurer la contribution d’un agrégat ou d’un secteur à un ensemble plus vaste, sachant que la somme des agrégats n’équivaut pas au total. Aussi, il devient téméraire de recréer des agrégats à partir de d’autres agrégats.

Il existe plusieurs pistes de solution pour parer à ces problèmes. Pour certaines analyses sommaires, les données en dollars courants peuvent être suffisantes et même souhaitables car elles reflètent la structure de l'économie aux prix actuels. Cela est particulièrement vrai si les agrégats étudiés n’affichent pas de grandes variations de prix ou si ces variations sont assez uniformes.

Pour qui veut s’en tenir aux données réelles et veut recréer des agrégations, une solution se trouve dans le calcul d’indices Fisher à partir des données Fisher existantes. En 1979, Erwin Diewert a montré que l'indice de Fisher était approximativement cohérent, et qu’ainsi il était possible de calculer des indices Fisher à partir d’agrégats déjà en Fisher, ce qu'il a appelé un « Fisher de Fishers ». Cette solution donne une approximation valable en autant que les agrégats entrant dans le calcul soient relativement consistants au niveau des prix (ce calcul est à proscrire, par exemple, s’il implique des séries d’inventaires).

Une solution plus « structurelle » consiste à jouer avec la fréquence de l’étalonnage. Comme l’additivité décroît à mesure que l’on s’éloigne de l’année de référence, réétalonner les séries de manière à rapprocher la période de référence peut aider à atténuer une partie du problème, sans toutefois rendre l’ensemble strictement additif. Il faut noter que dans le cas de données réelles basées sur des calculs d’indice en chaîne de Fisher, un changement de période de référence n’affecte aucunement les taux de croissance des séries réelles.

À défaut de pouvoir rendre additifs les niveaux, Statistique Canada propose, à l’instar du Bureau of Economic Analysis des États-Unis, une décomposition strictement additive des variations des agrégats pour les tableaux publiés des données réelles. La formule utilisée vise à repondérer les contributions des séries de manière à ce qu’elles deviennent strictement additives à la variation totale de l’agrégat

(11)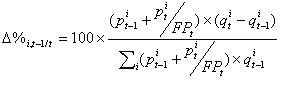

ou, dans une forme qui s'applique aux séries nominales et aux prix,

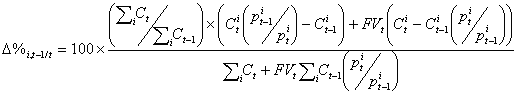
Cette formule est à l'origine des séries de contribution à la croissance en pourcentage publiées par la Division des comptes des revenus et dépenses. Une démonstration mathématique détaillée est disponible ici.

La contribution d'une série à la croissance du PIB

Questions et réponses

Quelle est la différence entre une période de référence et une période de base?

Les prix utilisés pour compiler les indices de volumes sont les prix de la période de base, tandis que la période où la valeur d’une série en dollars constants est égale à la valeur de ladite série en dollars courants constitue la période de référence. Dans l’ancienne mesure du PIB réel selon la méthode de base fixe Laspeyres, la période de référence et la période de base étaient les mêmes. Dans une mesure de volume en chaîne par contre, les deux périodes ne coïncident pas nécessairement. Par exemple, les séries du Fisher en chaîne de notre publication sont référencées en 1997 (les dollars courants égalent les dollars constants pour l'année 1997) mais la base correspond à un amalgame de la période courante et de la période qui précède immédiatement la période courante, puisqu’il s'agit d’indices en chaîne Fisher. La période de référence ne sert donc qu’à étalonner les séries et un changement de la période de référence ne modifie en aucun cas les taux de croissance des séries ou des agrégats. Le seul changement se trouve sur les niveaux, qui sont étalonnés sur une valeur différente.

Compte tenu de ce qui précède, on ne peut dire que les séries du Fisher en chaîne actuellement publiées sont « aux prix de 1997 », puisque les prix de la période de référence ne rentrent aucunement dans le calcul des trimestres précédents ou subséquents à l’année de référence. On peut cependant dire qu’il s’agit de séries exprimées en termes réels, donc soulagées des effets de prix, à un niveau tel qu’elles égalent le niveau de l’agrégat nominal pour l'année 1997. En d'autres termes, une série réelle dont l’année de référence est 1997 est l'équivalent d'une série nominale à laquelle on aurait enlevé l’effet prix depuis 1997.

Comment faire des comparaisons intertemporelles sur une longue période?

La formule de contribution à la variation en pourcentage exposée ci-dessus ne tient que pour une seule période. Pour utiliser la même formule sur une plus longue période de temps, il faut produire une valeur Fisher non chaînée, dont les bases de pondération correspondent aux périodes pour lesquelles on veut faire l'analyse. Par exemple, pour analyser la progression des biens de consommation durables entre le quatrième trimestre de 1996 et le quatrième trimestre de 2000, on peut calculer un indice Fisher dont la pondération est explicitement fonction des prix du quatrième trimestre de 1996 et du quatrième trimestre de 2000. Il s’agit, en quelque sorte, d’un indice Fisher à base fixe. Une fois cet indice calculé, la formule de contribution à la variation en pourcentage peut être directement utilisée.

De tels calculs pourront soit être effectués par les utilisateurs eux-mêmes, dans la mesure où ils auront à leur disposition toutes les séries comprises dans l’agrégat. Dans le cas contraire, ils peuvent être effectués sur demande par Statistique Canada.

Également, il est toujours possible de se servir des séries nominales. Les ratios ainsi trouvés reflètent la position d'un secteur aux prix du moment, et non aux prix d'une année de référence choisie arbitrairement.

---

Pour visualiser les documents PDF, vous devez utiliser le lecteur Adobe gratuit. Pour visualiser (ouvrir) ces documents, cliquez simplement sur le lien. Pour les télécharger (sauvegarder), mettez le curseur sur le lien et cliquez le bouton droit de votre souris. Notez que si vous employez Internet Explorer ou AOL, les documents PDF ne s'ouvrent pas toujours correctement. Veuillez consulter Dépannage pour documents PDF. Il se peut que les documents PDF ne soient pas accessibles au moyen de certains appareils. Pour de plus amples renseignements, visitez le site Adobe ou contactez-nous pour obtenir de l'aide.