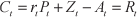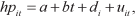Main article

View the most recent version.

1. Introduction
2. Valuing housing services
3. Estimates of housing services
4. Housing tenure and equity across age classes
5. Income and returns to equity
6. Conclusion

1   Introduction

Recently, concerns have been raised as to whether Canadians are prepared for retirement, as enrolment in pension plans has declined in the private sector and the recent financial crisis has placed greater financial strain on existing plans (Mintz, 2009). This has led to the development of a broad research agenda that is meant to expand our understanding of Canadians preparation for retirement (Mintz 2009).

Our objective is to consider not only the standard sources of income of working-age and retirement-age Canadians, such as employment and pension income, but also the more difficult to measure, implicit income derived from home equity. This is a potentially important source of income in retirement, given the substantial investment that Canadians make in their own homes. By the age of 65, nearly 8 out of 10 Canadians own their own home (Hou 2010), most without a mortgage. ¹  It is this accumulation of equity by many Canadians that helps to pay for the shelter (or housing services) consumed by homeowners. Therefore, the implicit returns from home ownership, while not a normal line-item in the family budget, pay for a necessary service that would have to be provided by other means.

This form of income generated by home equity should be distinguished from other income that might be generated by the capital built up in owner-occupied housing. In retirement, homeowners may choose to consume this capital. This paper does not address this additional potential source of income, but instead focuses on the contribution of home equity to the provision of housing services that would otherwise have to be purchased out of retirement income.

Income generated by owner-occupied housing is often ignored in the debate over the well-being of the retired, especially when the incomes of working and retired Canadians are compared. This is, in part, because it is difficult to measure the implicit returns from home ownership for individual groups of Canadians. Nevertheless, this form of income is measured at the level of the economy as a whole, where the implicit rent produced by homeowners is included in estimates of national income. This paper generates these measures for individual groups of Canadians at different stages in their life cycle.

The source of the unmeasured income derived from housing services on which this paper is focused originates from the equity that is built up in a home. Because the level of equity that is accumulated in homes may differ greatly between retirement-age and working-age Canadians, it is important to take this income into account—otherwise, the gap in the reported income across age groups that is derived using only traditionally measured sources may be overstated.

In this paper, we develop measures of both the value of housing services and the proportion of those services paid for by equity accumulated in owner-occupied housing. These measures are based on household data from the 2006 Survey of Household Spending (SHS) and the 2006 Census as well as on data from the 2005 Survey of Financial Security (SFS). These micro-data are used to construct measures of household income that, in addition to the sources considered in most studies (e.g., wages and salaries, dividends and interest, and pension payments), also include implicit income from home equity that pays for housing services. As well, because income is measured at the household level, it is possible to provide for different age profiles; this allows users to compare the incomes of working-age and retirement-age Canadians.

The remainder of the paper is organized as follows. The methods used to measure the value of housing services are outlined in the next section (Section 2). Since the estimates of housing services may be sensitive to underlying assumptions and data sources, two different methods for measuring housing services (user cost and imputed rents) and two different sources of data (the 2006 SHS and the 2006 Census) are used. Section 3, therefore, reviews the sensitivity of the estimates of housing services to different measures and sources of data. Section 4 outlines the proportion of households in rental housing and owner-occupied housing, respectively, and the average equity share for owner-occupied housing across age classes. In section 5, income and returns to equity across age classes are considered. It is in this section that the incomes of working-age and retirement-age households are compared by means of standard measures of income and measures of income supplemented by the implicit income generated by owner- occupied housing (Section 5). The paper concludes with Section 6.

2   Valuing housing services

The value of housing services provided by an owned dwelling can be estimated in two ways—by measuring either the capital service provided by the investment in a home or the implicit rent that ownership of a home generates to the homeowner. In this section, both methods of measuring housing services are discussed, as well as how they are applied to our primary sources of data, the SHS and the Census. The discussion progresses with an initial description of both methods and how they are fundamentally related; this is followed by a more detailed discussion of each method and its application to the data.

Capital services (C) and rents (R) in theory provide equivalent measures of housing services. Capital services provided by a home are equal to the value of the home multiplied by its user cost. The user cost of an asset in equilibrium can be thought of as the price that an owner of an asset would demand when renting out that asset. The user cost is used extensively in the productivity literature to value the capital services provided by assets such as machinery and equipment or buildings (Baldwin and Gu 2007). It is equal to: the opportunity costs of funds used to purchase the asset, the costs of depreciation incurred over the length of time the asset is rented, and any taxes on the asset; minus the expected appreciation of the asset. In more precise mathematical terms, the value of capital services provided by a dwelling at time t is given by

where: r is the rate of return to capital; P is the price of the dwelling; Z is depreciation, maintenance, insurance, and property taxes; and A is the expected appreciation in the value of the dwelling in year t.

User cost is therefore defined as the opportunity cost of capital (rP) and the out-of-pocket (Z) cost that the owner incurs (taxes, insurance, maintenance, and depreciation), less the expected increase in the value of the asset. The economic intuition that lies behind the user-cost formation is that economic agents, in setting the rental value of the asset, take into account both the cost of providing the asset (the opportunity cost of capital and the out-of-pocket costs such as taxes and maintenance), and set these against potential gains in the value of the asset. The higher the expected increase in the house value, the lower the rental price that must be charged in order to cover the cost of capital invested and the costs of maintaining the house for the rental market.

In equilibrium, the user cost of a dwelling will equal its rental rate, R. That is, all else being held equal, if the user cost of owning a dwelling is below the rental rate, there will be an incentive, on the margin, for economic agents to switch the asset from the rental market to the ownership market, placing upward pressure on home prices and downward pressure on rental rates. If the opposite holds, owners will have an incentive to sell and to enter the rental market. The extent to which user cost and rental measures of housing services tend to equate will depend on how active the rental and resale markets are (this, in turn, is influenced by the extent to which markets are distorted by rent control), the degree of uncertainty, and the size of transactions costs incurred in moving homes from one market to another (Gillingham 1983).

Regardless of which measure is employed, the primary technical challenge is to develop an accurate measure of housing services (Malpezzi 2002; and Garner and Verbrugge 2009). In order to estimate the value of housing services by means of user costs, an estimate of the cost of capital (r), other costs (Z), and the expected rate of asset appreciation (A) are required. While some problems need to be overcome in choosing an appropriate estimate for each of these, deriving an estimate of expected appreciation is the most challenging and the most critical since estimates of the user cost of capital are highly sensitive to its value (Garner and Verbrugge 2009).

The derivation of rents for owner-occupied dwellings also faces challenges, since rental values have to be imputed using those houses that are being rented at any time. Imputed rents are often derived from hedonic estimation techniques that relate rental prices to the characteristics of the dwelling. These estimates can be sensitive to omitted-variable bias (Malpezzi 2002). Moreover, for a significant portion of the stock of owner-occupied dwellings, the rental market is thin; the small size of this market increases the potential error in the estimation of imputed rents.

In light of the challenges associated with each of these measures of housing services, the strategy pursued here is to use both. Confidence will be raised that the estimates are near their true value if the user cost and imputed rent methods provide similar estimates of housing services. Before we address the estimates of housing services, a more detailed discussion of the methods used to estimate the user cost of capital and imputed rents is warranted, beginning with the user cost of capital.

2.1  User cost of capital

There are three essential elements in the formula that measures the user cost of capital: (a) the opportunity cost of capital; (b) depreciation, maintenance costs, insurance costs, and property taxes; and (c) the expected rate of appreciation of the asset. Each of these elements is addressed in turn below.

The first component, the opportunity cost of capital, depends on the price of the home and the rate of return on capital. In keeping with the spirit of the user-cost approach, the rate of return should be chosen as the cost of capital associated with financing the asset concerned. Assets can be financed out of both debt and equity, and different opportunity costs may be applied to each (Katz 2009). Housing debt is financed via mortgages; therefore, the mortgage rate will be used as the opportunity cost of capital for the debt portion of the financing required for housing. For the equity portion, the opportunity cost may be greater than the mortgage rate when the opportunity cost of funds is taken to be equity markets that return more than do mortgage markets, or less than the mortgage rate when the opportunity cost of funds is derived from assets such as savings accounts that yield less.

How households would optimally distribute their investments across asset classes if they sold the equity in their homes depends on their age profile and on other personal characteristics. Rather than delve into these issues, the same rate of return is applied to both the equity and debt portions. We use the 5-year fixed interest rate reported by the Bank of Canada (2010), averaged over the previous five years (2001 to 2005). ²  In 2006, this rate was 5.98% (Table 1).

The Z term in equation (1) includes other costs normally associated with the provision of housing space services in rental markets, including depreciation, insurance, repairs and maintenance, as well as property taxes. ³  Measures of depreciation, repairs, maintenance, and insurance are derived from the SHS ⁴  and applied to the Census. Both the SHS and the Census are used to measure property taxes, which are reported in both at the household level. Property taxes are included without alteration in our estimate of user costs. Together, insurance and property tax amounted to 1.04% of house value on average (Table 1).

Depreciation estimates are derived from two separate components. The first, and most important, is expenditures on improvement and alteration of the home ⁵  ; this component is reported by the SHS. Such expenditures are defined as those made with a view to increasing the value and the useful life of the property; they are therefore closely allied with the concept of depreciation. This measure includes expenditures with respect to the replacement of structural items (e.g., roofs and siding) and expenditures on what is referred to as improvements. While the term improvements suggests that this type of expenditure can take the form of new investments, rather than depreciation, it is in reality closer to the latter than to the former. The 'improvements' category includes expenditures related to required maintenance resulting from depreciation of a component of the property (i.e., replacement of aging windows or high-use areas such as flooring and kitchens). Furthermore, even when the expenditures on improvements involve a measure of 'upgrading', it can be argued that these expenditures are a component of depreciation, because structures are exposed not only to wear and tear but also to constantly changing standards of construction, fit, and finish. Without improvements being made to the condition of the dwelling and property in order to bring them into line with prevailing standards, the value of the home will fall behind that of comparable neighbouring properties as a result of obsolescence. This type of obsolescence is as much a component of the cost of capital that must be recaptured by a renter of capital as is physical depreciation.

At the household level, expenditure on improvements and alterations tends to occur unevenly over time, with large payments in some years and very little in others. ⁶  In order to provide a reasonable annualized estimate of depreciation, expenditures on improvements and alterations from the SHS are calculated as a share of the price of the home; this share is averaged across dwelling types, under the assumption that different types of dwelling depreciate at different rates. ⁷  This share is then multiplied by the value of each dwelling, according to dwelling type, in order to obtain an estimate of the annual value of depreciation. These same depreciation shares across dwelling types are applied to the Census.

The second component of depreciation accounts for long-term structural deterioration that cannot be addressed through expenditure on improvements and alterations. This additional contribution to the depreciation rate is set to 0.5% of the value of the dwelling. This depreciation rate implies the expected life of a dollar invested in a house to be 75 years, on the assumption that 75% of the value of the dwelling is attributable to its structure and a straight line depreciation rate. We assume that land does not depreciate. ⁸  Together, the estimates for improvements, alterations, and this additional component produce a measure of depreciation of 2.2% (Table 1). Alternate procedures produce very similar results. ⁹ 

The price of a dwelling is composed of the value of the structure, which depreciates over time, and the value of the land, which is usually treated as not being subject to depreciation. This implies that, in locations where land accounts for a significant portion of the value of a dwelling, the amount of depreciation could be overestimated. However, for the purposes of this study project, it is assumed that depreciation rates are constant across all locations.

In addition to depreciation, maintenance is also a cost that must be taken into account in estimating rental value. The SHS includes annual expenditures on repairs and maintenance, defined as expenditures to "…keep a property in good working order or maintain its appearance." ¹⁰  These include standard expenditures on repairs to, and maintenance of, the dwelling (e.g., repairs to roofs, plumbing, or fences). ¹¹  These expenditures, when taken as a share of price of each dwelling and then averaged across dwelling types, amount to 0.23% of the house value (Table 1). These ratios are then multiplied by the price of each dwelling in order to arrive at an estimate of annual maintenance expenditures. These same shares are also used to estimate repairs and maintenance expenditures under the Census.

The final variable in the user-cost formula is the expected rate of appreciation of the asset. In previous work done in this area, deriving measures of appreciation has offered the greatest challenge. For instance, Garner and Verbrugge (2009) use forecasted increases in house prices to measure the expected rate of asset appreciation, but find the resulting user costs to be negative for a broad range of house values as a result of the large size of the expected rate of appreciation. Similarly, Barham (2004) reports negative user costs in Ireland, as do Jorgenson and Nomura (2005) in Japan, and Jorgenson et al. (2005) in the United States [All cited in Schreyer (2009)].

Garner and Verbrugge (2009) use an alternate technique that suggests the best measure of the rate of appreciation in house values is the trend consumer price index. They derive an estimate of the expected appreciation of housing assets by equating the rental price that a homeowner would expect to obtain for his or her house (derived from a large-scale survey), along with a user-cost estimate, with standard estimates for the rate of return and the depreciation, to which an unknown expected appreciation value is applied. The solution to the expected appreciation value that equates the rental value and the user cost is taken as the measure of expected appreciation used by homeowners in assessing rental values. This value is very close to the trend consumer price index. While Garner and Verbrugge (2009) are puzzled by this result, since it implies a zero expected increase in real housing prices, Schreyer (2009) suggests a rationale for the finding, arguing that, in the long run, real changes in asset prices can be reasonably expected to equal zero. The empirical evidence tends to support this proposition. For instance, Akerlof and Shiller (2009; cited in Schreyer 2009) find that, between 1990 and 2000, the real rate of appreciation in house prices was 0.2% per year.

In order to test the sensitivity of the results to alternate values of the expected rate of appreciation, several different rates are employed. These are based on the following: the trend CPI over the 1981-to-2006 period (3.2%); the nominal average annual increase in house prices over the same period (4.7%); and the nominal increase in house prices over the 1996-to-2006 period (5.9%). The former are more relevant if expectations are based on long-run trends. The latter might be expected to be the most relevant, if Canadian homeowners in 2006, the year being used for our analysis, were making use of the actual appreciation in house prices that took place during the previous decade to form their expectations of the trend in house prices.

The 2001-to-2006 period was one of rapid appreciation in Canadian house prices. ¹²  Tsounta (2009) finds real house prices increased significantly between 2003 and 2006. The Census, using a longer period, tells a similar story (Chart 1). From 1981 to 2000, average house values in Canada ranged between $150,000 and $200,000 (in 2005 dollars). By 2006, the average house price had risen to about $260,000, well above levels reported over the previous two decades.

The rapid rise in house prices may mean that recent prices do not reflect market fundamentals. In periods when housing prices become frothy, there is greater reason to believe that user costs derived from house prices may diverge from rental markets—because adjustments between the two require a period of correction that arises from inherent frictions in housing markets. To overcome this potential criticism of the user-cost method, estimates are derived of 'fundamental' house prices—which are essentially smoothed house prices that are meant to remove what may be short-run aberrations resulting from temporary overpricing or underpricing of housing markets. ¹³ 

2.1.1  Estimation of fundamental house prices

An estimate of the long-run fundamental house price (hp), which treats prices as being determined by local circumstances, a time trend, and random fluctuations, is written as:

where a is the intercept term, t is the time trend, d_i is a dummy variable for market i, and u is an error term. Rather than mechanically predict house prices solely on the basis of time trends, we follow Gao, Lin, and Na (2009), and replace the time trend in the model with additional variables expected to determine housing prices in the long-run, namely, income levels and mortgage costs:

where inc_it is mean household incomes in market i, and m_t is the mortgage cost in terms of monthly payments for one dollar of the mortgage loan amount for a 5-year fixed interest rate in year t for a standard 25-year mortgage.

The Gao, Lin, and Na (2009) specification is augmented further in two ways. First, added to the model is a measure of the terms of trade. For a small, open economy like Canada, shifts in the terms of trade have been shown to contribute to real-income growth (Macdonald 2008) and are expected to influence the prices of non-tradable goods such as housing. That is, as the terms of trade improve, households see an increase in the real value of their income. As a result, higher household income contributes to rising housing demand and, thus, to higher housing prices. Second, the employment rate is added in order to take into account broader macro-economic conditions that might also influence house price levels. Hence, the finalized model is specified as follows:

where tot_it is the terms of trade for each market i (or each province, in this case) in year t and emp_t is the national employment rate in year t.

To estimate the model, housing prices and household incomes are taken from the 1981 to 2006 Censuses. These are estimated across geographic markets i, which are defined as metropolitan areas (census metropolitan areas (CMAs) and census agglomerations (CAs)), and the non-metropolitan portion of provinces are divided into metropolitan influenced zones. Metropolitan influenced zones are, broadly, rural areas divided into four classes on the basis of their level of commuting interaction with metropolitan areas (strong, moderate, weak, or zero commuting). All geographic units are defined according to the 2006 Census geography. The terms of trade data are obtained from the provincial economic accounts, while the employment rate, for those aged 15 years and over, is taken from the Labour Force Survey. Finally, the 5-year fixed mortgage lending rate is obtained from the Bank of Canada series of historical mortgage rates (Bank of Canada 2010).

The 5-year fixed mortgage lending rate is used to calculate the monthly mortgage cost. The monthly mortgage cost for borrowing one dollar is calculated as follows:

where rate_t is the five-year fixed mortgage lending rate. It is assumed that payments are made on a monthly basis and that the mortgage is amortized over a 25-year period.

The results are presented in Table 2, including interaction terms on income for selected metropolitan areas. As expected, mean household income, the national employment rate, and the terms of trade are positive and statistically significant, whereas the coefficient on mortgage cost is negative and significant. Rising incomes, employment, terms of trade and lower interest rates are associated with higher housing prices. A one percent increase in mean household income is associated with a 0.37 percent increase in the fundamental house price. A one percentage point increase in the employment rate is associated with a 3.3 percent increase in the fundamental house price. An increase of one index point in the terms of trade increases the fundamental house price by 1 percent. A one percent increase in the mortgage cost results in a 0.198 percent drop in the fundamental house price.

All of the listed interaction terms between household income and region, except those for Vancouver, are statistically different from those for the reference region, St. John's, Newfoundland and Labrador, at the 10 percent level of significance. In all of these regions, an increase in the region's mean household income will lead to an increase in the fundamental house price.

The actual and fundamental (predicted) house prices for selected areas for the period from 1981 to 2006 are presented in Chart 2 to 10. In most metropolitan areas, while there was a tendency for actual house prices to deviate from the fundamental house price over time, there was also a tendency for prices to return to predicted levels. In some metropolitan areas, the deviations around the long-run fundamental predicted price were quite small. This was typically true of metropolitan areas in provinces that saw large improvements in their terms of trade since 2001, Alberta and Saskatchewan. Their actual and fundamental house prices were very similar over time, and almost equal between 2001 and 2006. ¹⁴  In Halifax, the actual price is particularly close to the fundamental price over the period, except in 2006, when it is higher.

Of particular interest is the difference between actual and predicted house prices in 2006. Large differences are an indication that the 2006 prices used to derive user costs may have been out of step with economic fundamentals. In the selected metropolitan areas presented, house prices were above predicted levels, save for those in Saskatoon, Calgary, and Edmonton. In percentage terms, Vancouver has the largest deviation between actual and predicted prices, with the former being 18 percent higher than the latter. Montreal follows closely, its actual prices eclipsing fundamental prices by 17 percent. Actual prices in Halifax are about 14 percent above predicted levels, whereas this deviation was somewhat lower in Toronto, Winnipeg and Ottawa—at between 8 and 9 percent. While these deviations are similar in magnitude to deviations observed in previous years between actual and predicted house prices, they are large enough to warrant investigating whether using predicted house prices, instead of actual house prices in 2006 has a significant influence on our estimates of housing services.

2.2  Imputed rents

Imputed rents are estimated using both the SHS and the Census to test for the sensitivity of the estimates to alternate data sources. The models applied to the Census and the SHS are quite similar in functional form and the variables included in their specifications. Following the literature, a semi-log structure is used, whereby the contribution to utility of any one dwelling characteristic will depend on the value of the others. ¹⁵  Both models use two classes of variables, namely, measures of location and quality of the dwelling (e.g., the number of rooms). The models differ in terms of their sample size and the availability of some variables across the two data sets.

The hedonic rent model estimated on the basis of the SHS is specified as:

where rent is the value of monthly serviced rental payments, which includes payments (i.e., water, electricity and fuel). As noted above, the right-hand-side variables can be divided into two broad classes. The first class measures the characteristics and quality of dwellings (i.e., the number of rooms and bathrooms in a dwelling and the type of dwelling), while the second class takes into account the location of the dwelling (i.e., the size of the urban area in which the dwelling is located (u) and the province in which the dwelling is located (p)). To estimate the model, the 2005 and 2006 samples are pooled, with a binary variable for year (t) included in order to account for increases in rent over time that are not related to quality and location. The sample is restricted to the following: households that have rented and occupied their dwellings for 12 months; dwellings that are not in need of major repairs; and dwellings for which the rent has not been reduced over the previous 12 months.

The results in Table 3 conform broadly to expectations. Rents tend to be higher for dwellings with more rooms. The excluded category is six-room dwellings, hence the negative coefficients for dwellings with fewer than six rooms. The number of bathrooms is also positively associated with higher rents. Dwellings with two bathrooms rent on average for 17% more than dwellings with only one bathroom, all other characteristics held constant. The type of dwelling also influences the rent level, with most classes commanding higher rents than apartments in low-rise rental buildings, the reference category. The highest rents are charged for apartments in high-rise buildings; these rents likely reflect the more centralized locations of these structures. Rents are also higher in larger urban centres: rents in urban centres with a population greater than one-million people are 36% higher than those in rural areas, all other characteristics held constant. This result is consistent with the hypothesis that higher average incomes in larger centres are capitalized in land values. Finally, despite this fairly parsimonious specification, the model explains 43% of the variation in rental rates across a sample of 6,500 observations.

As noted above, the Census-based model is similar to the one applied to the SHS. The Census-based model takes into account the effect of the number of rooms and bedrooms, but not the effect of the number of bathrooms, on rental rates; it also takes account of the type of dwelling and the size of the urban area in which the dwelling is located. In addition, the Census-based model includes the period of construction of the dwelling (periodofcons) and takes account of whether the dwelling requires minor or major repairs (condition). ¹⁶  Because the Census has a much larger sample size, included in its specification is a much more detailed set of variables that take into account the effect of location. The model includes a series of neighbourhood ¹⁷  (neighbourhood) characteristics hypothesized to influence rental rates (e.g., the median income in the neighbourhood, the proportion of owner-occupied dwellings, and the proportion of university-educated adults). Finally, fixed effects at the census subdivision level are included in order to account for unobserved characteristics of locations (c). ¹⁸ 

The results from the Census of Population are broadly consistent with those of the SHS (Table 4). With respect to dwelling characteristics, the number of rooms and bedrooms (conditioning on their number) has a positive, but declining, marginal effect on rental rates. Rental rates are also generally higher for single detached dwellings and lower for older dwellings.

As with the SHS-based model, the Census-based model takes into account the influence of location; however, given its larger sample, it includes more detailed location-related variables. Dwellings in neighbourhoods with higher median incomes, a higher proportion of owner-occupied dwellings, a greater share of population that is university educated, and a larger proportion of apartment buildings (particularly those over five-stories in height) tend to have higher rental rates. ¹⁹  In contrast, neighbourhoods with a younger population as well as a greater proportion of lone-parent families, low-income families, and owned dwellings tend to have lower rental rates. ²⁰  Finally, unlike the SHS, the Census indicates that rental rates do not increase in proportion to the size of urban area; this result is likely attributable to the inclusion of municipality fixed effects and detailed neighbourhood characteristics. Overall, the Census-based model explains about 33% of the variation in rental rates; this rate is lower than that for the SHS, but nevertheless relatively high with respect to a cross-sectional estimation based on large micro-data sets.

Both the SHS-based and Census-based models are used to impute rents for owner-occupied housing. These imputed rents, however, include services provided by landlords that are not consistent with the user-cost-based measure of housing services. That is, the user cost of a dwelling does not include expenditures on utilities (i.e., water, fuel, and electricity) and other services provided by landlords (i.e., janitorial services, parking, and depreciation on furniture and appliances). As imputed rent is calculated gross of these services, they have to be deducted for comparability to the estimates of the user cost of housing.

To estimate imputed rent net of services provided by landlords, or space rent, information from the SHS and the National Accounts is used. The SHS serves to measure the value of utilities in imputed rent. To this end, the utility share of imputed rent for owner-occupied dwellings other than apartments is calculated. Owner-occupied apartments are treated separately. The mean of these shares is taken across provinces and multiplied by imputed rent to obtain a measure of the level of utilities for each owner-occupied dwelling. This value is then subtracted from imputed rent to obtain space rent.

Owner-occupied apartments consist mostly of condominiums, whose fees tend to include utilities. Since this may result in bias, the utility share of owner-occupied apartments that might be calculated from the SHS is not usable. Instead, the ratio of the utility share of rents for rental apartments to the utility share of utilities for other rented dwellings is taken, and this figure is multiplied by the utility share of owner-occupied dwellings (other than apartments), in order to obtain a utility share for owner-occupied apartments. This result is multiplied by imputed rent to obtain a measure of the level of utilities expenditures; this result is in turn subtracted from imputed rent.

Imputed rent for apartments is further adjusted by subtracting expenditures on janitorial services, parking, and depreciation of furniture and appliances. These adjustments are derived from the National Accounts on a national basis. For other types of dwellings (e.g., detached residences), these adjustments are not made, because imputed rents are unlikely to include these costs (e.g., janitorial services).

3   Estimates of housing services

The discussion now turns to providing estimates of housing services. To assess the sensitivity of the estimates to different methods and sources, both the user cost of housing services and imputed rent from both the SHS and the Census are presented. The estimated value of housing services from the SHS across house value quintiles is set out in Table 5.

For the user-cost estimates, the key variable influencing the value of housing services is the assumed rate of appreciation for house prices. Owing to uncertainty regarding the true value of the expected increase in house prices, we use a range of values. These are centred on an average increase of 4.7% in nominal house prices over the 1981-to-2006 period, which is rounded to 5% for our estimates. User costs are also estimated on the basis of a rate of appreciation of 4%, which is near the CPI growth of 3.2% over the same period and therefore is close to an expectation of a zero real increase in house values, particularly when transaction costs are taken into account. Finally, user costs are estimated for an expected rate of house price appreciation of 6%, which is near the average annual nominal increase in house prices of 5.9% over the 1996-to-2006 period, and presumes that the expectations of home buyers are based on more recent information.

Applying alternative rates of expected house price appreciation has a significant effect on user costs. A 4% rate resulted in an average imputed value of housing services of $15,997 per year (column 1); this is more than one-third higher than the $10,116 value estimated for the 6% rate (column 3). ²¹  The question at hand is which of these estimates is the most reasonable. Ultimately, imputed rents will be used to arbitrate amongst these alternatives. However, before doing so, the impact of alternative assumptions, in particular the implicit assumption that house prices are in equilibrium, is examined.

Nominal house prices increased at an annualized rate of 9.8% between 2001 and 2006 (2001 and 2006 Censuses of Population); this figure suggests that user-cost estimates in 2006 may be underpinned by heightened expectations of future asset appreciation. As a result, the expected appreciation in house prices based on longer-term trends in house prices (i.e., columns 1 and 2) may be too low and the resulting estimates of user costs too high.

There are two possible solutions to this problem. The first is to attempt to estimate expected house price appreciation by applying the recent nominal rate of growth in house prices between 1996 and 2006, which yields the results set out in column 3. The second solution is to follow Schreyer (2009) and assume that expected appreciation follows long-term trends. In this study, however, contrary to Schreyer, no assumption is made that house prices are in equilibrium in 2006. Rather, the long-run expected rate of appreciation is applied to the long-run fundamental value of the house. This yields a user-cost estimate associated with a longer-run equilibrium. When predicted fundamental house prices and the long-run appreciation estimate are used, the average estimated value of housing services is slightly higher ($12,166 in column 4) than the estimate based on the actual 2006 house price combined with the recent rate of house appreciation ($10,116 in column 3). In contrast, when the long-run expected appreciation is used along with 1% decline in the interest rate from discounts in the mortgage rate, the result is equivalent to the estimate in column 3 ($10,116).

The alternative to the user-cost-based measure of housing services is imputed rents. Overall, imputed rents tend to be below user costs. The average value of imputed rent was almost $8,400, well below the average user-cost estimate of $12,166, which is determined on the basis of the fundamental house price, or the average user-cost estimate of $10,116, which is determined on the basis of recent price increases and the 2006 house price.

Much of this difference is attributable to homes whose values fall into the upper two quintiles, especially into the top quintile. Homes priced in the middle quintile and in the lower two quintiles have similar values for imputed rents and for the user cost of housing services—when the 6% rate of appreciation is used. The latter tend to be below imputed rents for the lower two house-price quintiles, about equal for the middle quintile, and above for the upper two quintiles. Still, for the top quintile of homes, that is, homes valued at $400,000 or more, the user-cost estimates are about $10,000 greater than the imputed rent estimates; this raises the question of which of the two estimates for the top quintile is more reliable.

The problem with the estimates of imputed rents for homes valued in the top quintile is that these come from a section of the rental market that is very thin. In order to assess the significance of this problem, Census data are utilized to predict the value of rental dwellings according to the characteristics of homes in the owner-occupied stock. Out of the total of 747,952 (unweighted) rental dwellings in the Census sample, only 254 were estimated to have a home value in the top quintile. This is a market within which there are very few rental alternatives to owning a home of a size, quality, and location to warrant its high value.

It is also of note that the rents charged for homes that match the characteristics of owner-occupied homes valued in the top quintile are close in value to the average user cost for this group. Using a 6% appreciation rate, and user cost estimated from Census data (Table 6), estimated housing services for the top quintile of dwellings on the basis of the user-cost approach was estimated to be $20,649 and the imputed rent for the top quintile was estimated to be $10,702. Yet, the average rent for homes whose characteristics match the top quintile is $17,000, ²²  a figure which is closer to the user-cost estimate than to the imputed-rent estimate. Those rental homes that match the characteristics of homes in the top-value quintile are quite different from the average rental home, and these characteristics may not be fully captured by the hedonic rent model. This, in turn, may lead to an underestimation of the value of housing services for homes in the top quintile.

For the remainder of the analysis, a 6% expected rate of appreciation is used to derive an imputed value of housing services. This rate, which matches the 10-year nominal rate of increase in house prices between 1996 and 2006, provides an estimate of the value of housing services that is closest to imputed rent, in particular with respect to the middle three quintiles. It is also an estimate that can be derived from an assumption of a lower interest rate than the fixed five-year rate and a longer-run expected rate of housing price appreciation. While the SHS is a starting point for deriving estimates of user costs and rents, the Census provides an alternative means to estimate these values. As a result of its larger sample size, estimates from the Census afford a more detailed breakdown of incomes across a greater number of socio-demographic classes. Table 6 compares the estimates of user cost and imputed rents for the Census and the SHS, utilizing the house-price quintiles used for the SHS.

Both sources of data provide similar estimates of housing services. The user-cost estimates from the Census are marginally lower than those from the SHS for the middle quintile and the bottom two quintiles. Estimates from the two data sources tend to vary largely as a result of differences in estimates of house prices. The other components of user costs, with the exception of property taxes, are either derived from the SHS or have a common source (e.g., five-year mortgage interest rates reported by the Bank of Canada). ²³  Imputed rent estimates from the SHS and the Census are also quite similar to the Census estimates.

In summary, the SHS and the Census provide similar estimates of housing services, using both the user-cost and imputed-rent measures. While user costs and imputed rents provide relatively similar estimates of housing services for homes valued below the top quintile, this is not the case for the top quintile. For these more expensive homes, estimates of user-cost far outstrip imputed rents. However, given the thin rental market for these homes, imputed rents are likely to provide an unreliable estimate of their value. Hence, unless otherwise noted, housing services will be measured using the user-cost approach for the remainder of the study.

4   Housing tenure and equity across age classes

The income that a particular group of households derives from home ownership depends on the proportion of that group owning homes and the value of the home equity that they possess. Table 7 presents the proportion of renters and owners, the proportion of homes owned with and without a mortgage, and the average equity share, across age classes

As expected, home ownership was found to rise with the age of households. For households whose reference person is between ages 20 and 29, 70% are renters. This share falls steadily to 22% for the 50-to-59 age class and then rises again to 32% for households in the 70-plus category.

The proportion of households owning their homes that have a mortgage also declines steadily with age. Nearly 9 out of 10 homeowners between ages 20 and 29 and between ages 30 to 39 have a mortgage. For older age classes, the proportion of households with a mortgage declines steadily: for households with a reference person aged 70 or more, only about 1 in 10 has a mortgage. To estimate the equity share by age class, however, requires an estimate of the value of the mortgage held by homeowners, which is not provided by the SHS.

To estimate the equity share for dwellings with a mortgage across age classes, the 2005 SFS is used. From the SFS, the equity share of house values for households with a mortgage across age classes can be estimated. The effect of additional cross-classifications (e.g., income class and house value class) on equity shares was tested, but these proved to have only a small effect after the age of the reference person in the household was taken into account. Equity shares from the SFS were, in turn, applied to the SHS (and to the Census) by age class for owner-occupied dwellings with a mortgage. These results were combined with information on homeowners without a mortgage, whose equity share is, by definition, 100%, to obtain overall equity shares by age class.

As expected, equity shares were found to increase steadily with age, as homeowners pay down the principal on their mortgages. Equity shares rise from a low of 40% for the youngest age class to 90% or more for the two oldest age classes. The majority of homeowners in their retirement years have paid off their homes and are able to rely on returns from their home equity to implicitly pay for their housing services.

5   Income and returns to equity

The analysis now turns to measuring the income generated by home equity that pays for the consumption of housing services as well as its relative contribution, across household age classes. Gross and net incomes by age class derived from the SHS and the Census are reported in Table 8.

In this table, comparisons are made across age groups for a particular year with and without allowance for the implicit income being generated from home ownership. The income differences that are reported are due to many causes that stem from generational or age effects. Estimating the effect of home ownership as is done here does not capture the impact of home ownership on the income replacement rates of retirees. That would require a cohort to be tracked over time rather than a number of different cohorts to be compared at a given point in time. However, the comparisons do provide an indication of whether failure to consider the implicit income provided by home ownership distorts cross-sectional comparisons of well-being.

Because income derived from owner-provided housing is not taxed, comparing incomes across groups requires that calculations be made of income net of taxes. Moreover, to provide greater comparability of the income available for consumption between working-age and retirement-age households, incomes are also measured net of payments for employment insurance and life insurance as well as payments into annuities and public and private pension plans, since these are not required after retirement. There are, of course, other forms of payroll deductions (e.g., for union dues) and savings (e.g., education savings plans for children) that may differ across working-age and retirement-age classes, but these are not taken into account here.

Both the SHS and the Census provide measures of total household income and income-tax payments. As a consequence, both gross income and income net of income taxes can be reported for both (Table 8, Panels A and B, columns 1 and 2). The SHS and the Census provide broadly comparable measures of household income. Compared to the Census, gross incomes reported by the SHS tend to be higher for younger age classes and lower for older age classes. These differences are mitigated somewhat by taking taxes into account; but, in general, incomes in the retirement-age classes (60-to-69 and 70-plus) after taxes are about 17% higher for the Census than for the SHS. Since the Census is based on a much larger sample of households, more emphasis is placed here on the Census estimates.

The SHS asks respondents to itemize their payments for life insurance, annuities, employment insurance, and public and private pension plans, whereas the Census does not. To estimate net income less these payments, the ratios found in columns (3) and (2) from the SHS (Panel A) presented in Table 8 are applied to the Census (Panel B).

Using the SHS, the effect of these payments on income available for consumption varies significantly by age class. For those households in the 40-to-49 age class, average net income reported by the SHS falls from $65,800 to $60,600, whereas, on average, income declines only from $34,700 to $33,800 in the 70-plus age class. Taking these payments into account affects the relative standing of seniors.

A comparison of incomes across age classes indicates that there is a difference in incomes between working-age and retirement-age classes. Utilizing income from the Census net of income taxes and other payments (column 3), household incomes in the 40-to-49 age classes were about $62,000 per year. This compares to incomes in the 60-to-69 age class and the 70-plus age class of $50,500 and $39,400, respectively. The relative income ratio for the 70-plus age class was therefore 63% using the Census and 56% using the SHS.

Of primary interest is the extent to which the relative income of seniors changes when returns to housing equity are added to income net of taxes and other deductions. Panel A in Table 9 reports net income (as defined by column (3) in Table 8) for all households as well as for renters and homeowners across age classes from the SHS. For homeowners, returns to equity are added. These are defined as the user-cost-based value of housing services, utilizing an assumed 6% expected rate of appreciation in house prices, ²⁴  multiplied by the equity share across age classes. ²⁵ 

Returns to equity, while generally increasing with age, tend to fall back somewhat for the oldest household age class. In general, returns to equity increase with the age of households because households' equity share and house values increase as well. However, unlike equity shares, house values do not increase monotonically. They increase until the 50-to-59 age class ($315,000) and then decline for the two oldest age classes ($305,000 for the 60-to-69 age class and $252,000 for the 70-plus age class). As a result, while returns to equity generally increase with age, they fall off for the oldest age class, because of lower house prices.

Despite this decline in return to equity, the magnitude of the gain for seniors that occurs when the implicit returns to equity are recognized is large. For homeowners, implicit returns on equity increase incomes by 13% and 15% for the 60-to-69 and 70-plus age classes, respectively. This compares to 4% for the 20-to-29 and 7% for the 40-to-49 age class. As a result, the ratio of income of households classified above age 70 increases relative to those younger than 60 from about 0.55 to 0.58.

While Panel A of Table 9 provides a measure of average household income across age classes and by tenure type, it does not take into account the size of households. Typically younger households are larger, composed of couples with children, while the youngest and oldest households are more likely to be persons living alone or couples with no children. To take into account household size, we use the OECD method of dividing income levels by the square root of the size of the households. Underlying this formulation is the assumption that there are economies of scale in households—less consumption is required per person as households increase in size. Panel B presents household income levels after controlling for household size. The net result is that the relative income of senior homeowners increases even more—with rates ranging from 70% to 77% for the 70-plus age group, according to whether the 40-to-49 or the 50-to-59 age classes are used as references.

As noted above, the Census provides an alternative source of information on household income and on the value of housing services. Table 10 contains estimates of net household income, both not adjusted and adjusted for household size, for the same age and tenure classes presented in Table 9. Returns to equity increase net incomes by 10% and 12% for households in the 60-to-69 and 70-plus age classes, respectively.

While Census estimates of the proportional gains in net incomes from returns to equity tend to be lower than those derived from the SHS, the ratio of relative income of retirement-age households to relative income of working-age households tends to be higher. Relative net incomes are 62% for households in the 70-plus age class, and this rises to between 65% and 66% when the proportion of housing services implicitly paid for by returns to equity is taken into account. When household size is taken into account, the relative income rises further, to between 74% and 82% for net income and to between 78% and 87% for net income plus returns to equity.

As a final check of the sensitivity of the results to alternative methods, Table 11 presents net incomes plus return to equity based on the level of housing services estimated through imputed rents for homeowners. As noted previously, compared to user-cost estimates, housing services for more valuable homes appear to be underestimated when one uses imputed rents. However, a comparison of Tables 10 and 11 suggests that the method of measuring housing services has no substantive effect on the findings.

As a result of the positive association between household income and house values, household income and implicit income from home equity may be positively related. To test this, income and net returns to equity are presented by household income quintile and age class in Table 12, where income quintiles are defined according to gross household income. As expected, as house values increase across income quintiles, so too do returns to equity in level terms. However, as a proportion of total income, returns to equity are more important to lower-income households. A household in the lowest income quintile and in the 70-plus age class derives, on average, 17% of its income from home equity, whereas a household in the same age class but in the top income quintile derives 7% of its income from home equity. Home equity is potentially an important source of income for lower-income households and thus home ownership represents an important demarcation between lower-income and higher-income retirement-age households.

For households that fall into the lowest income quintile, home ownership is far less prevalent than higher income. In the lowest income quintile, 43% households in the 70-plus age class are renters (Text table 1, Appendix I). This compares to 14% of households in the middle income quintile and 7% of households in the top income quintile. Moreover, because retirement-age households are more prevalent in the lower-income classes, renters make up a significant share of these households—about one in five households in the 70-plus age class are in the lowest income quintile and are renters.

House values also vary significantly across provinces and metropolitan areas, leading to potentially large variation in returns to equity. Across provinces, average home values were lowest in Newfoundland and Labrador and highest in British Columbia, at $112,000 and $412,000, respectively (Table 13). As a result, for homeowners, returns to equity in British Columbia were the highest, at $7,300, boosting net income by 12%. In Newfoundland and Labrador, returns to equity were the lowest, at $2,000, increasing net incomes there by a more modest 4%. The effect of taking into account returns to home equity is to increase the incomes differences across provinces. For instance, before taking returns to equity into account, average net income for homeowners in Ontario was 46% above that for homeowners in Newfoundland and Labrador. However, after taking returns to equity into account, this difference widened to 50%. ²⁶ 

Across census metropolitan areas, average house values vary from a low of $115,000 in Saguenay to a high of $519,000 in Vancouver (Table 14). For homeowners, net incomes are highest in Calgary, at $84,800, well above those in other metropolitan areas. To this, returns to equity add $6,100, or 7%, to total net income. This compares with the figure for Saguenay, whose average homeowner household income was the lowest, at $53,600, and where returns to equity contributed only $1,900, or 4%, to total net income. Vancouver experienced the greatest increase in incomes from home equity—there, home ownership increases incomes on average by $8,900, or 13% of total net income.

6   Conclusion

This paper estimates the implicit income generated by the home equity of working-age and retirement-age households. In so doing, it expands our understanding of Canadians' preparation for retirement by taking into account the services that homeowners realize as a result of having invested in a home.

Housing services make an important contribution to household income. When estimates of the services provided by the equity invested in housing are added into traditional estimates of income, the income of retirement-age households is increased by 10% to 13% for those in the 60-to-69 age class and by 12% and 15% for those in the 70-plus age class.

This additional income reduces the difference in income between working-age and retirement-age households that own their own homes. According to the Survey of household spending, net incomes decline by about 45% between the peak household earning years and the 70-plus retirement-age class. This figure is reduced to 42% when the contribution of housing services is taken into account. The Census provides a similar picture, with the gap in incomes being 38% when net income alone is considered, and about 35% when one accounts for housing services.

Taking household size into account further reduces the difference in income between working-age and retirement-age households. According to Census data, incomes of retirement-age households are between 22% and 13% below that of working-age households when housing services are included.

It should be stressed that this estimate of the implicit income is only part of the value that home ownership provides in retirement. It is the equivalent of housing services that are provided to the retiree from the investment in a home. But this investment provides both ongoing services and an asset with a value that can be realized either to generate additional income or as a value taken in the form of a bequest.

At its root, this analysis suggests that the housing services realized by homeowners are an important source of well-being for retirement-age households.