Household Expenditures Research Paper Series
Survey of Household Spending Modelled Annual Statistics, 2010 to 2017

1. Introduction

Since 1997, the Survey of Household Spending (SHS) has collected detailed spending information and selected information on dwelling characteristics and household equipment. In 2010, the SHS underwent a major redesign. Due to the new survey design, certain statistics which were made available to users for reference years prior to 2010 are no longer published for years 2010 onward. These statistics include the annual average expenditure per reporting household and the annual proportion (or percentage) of households reporting. The number of households who incurred spending in the reference year (the number of households reporting) is not available for many categories as a result of the new survey design, which precludes the calculation of these two statistics. 

To help fill this data gap for users, a statistical model was developed in order to produce approximations of these statistics. The SHS modelled annual statistics are now available in tables A, B, and C in the appendix of this document as well as in Microsoft Excel format.

This document provides information for users of the SHS 2010-2017 modelled annual statistics. It explains the context for the modelled annual statistics, describes the tables containing these statistics, and details the methodology behind the statistical model.

2. Context

Since 2010, the SHS collects data using two methods. The first is a questionnaire administered through a personal interview using recall periods that vary by type of expenditure (last month, last 3 months, last 12 months, or amount of last payment). The second is a daily expenditure diary which is completed by a sub-sample of households during a 2-week^Note  period that starts the day after their in-person interview. The interview is used to collect larger or less frequent expenditures, as well as regular payments. The diary collects smaller or more frequent expenditures that would be difficult to recall during a retrospective interview. Data collection is carried out on a continuous basis from January to December from a sample of households that is distributed over 12 monthly collection cycles.

Prior to 2010, the SHS collected information using a personal interview that was conducted during the first quarter of the year during which the household reported expenditures for the preceding calendar year. 

The SHS is designed to produce annual estimates. With the new survey design, expenditures collected with a reference period of less than 12 months are annualized in order to produce annual estimates of total (aggregate) expenditures and average expenditures per household. For example, expenditures reported in the interview using a 3-month recall period are multiplied by 4 and expenditures reported in the 2-week diary are multiplied by 26.

Annualized values for expenditures collected using shorter reference periods are not intended to be representative of an individual household’s annual spending. The annualized values may over-estimate actual annual spending for some households and under-estimate it for others. As well, some households who actually purchased an item over the course of the year may have an annualized value of zero. This can happen if their spending fell outside the specified recall period in the interview or the two-week diary reporting period and therefore, was not reported. For this reason, the SHS does not provide the number of households reporting a category of expenditure during the reference year when the expenditure is collected with a reference period of less than 12 months.



Table 1 shows that the calculation of the average expenditure per reporting household and of the proportion of households reporting requires the number of households reporting expenditures in a given category. As described above, the number of households reporting expenses over a short reference period is generally lower than it would be with a 12-month reference period. Using this value as a denominator will result in an observed average expenditure per reporting household that is too high and an observed proportion of households reporting that is too low compared with the true annual statistics. Without using modelling methods, it is not possible to accurately estimate an annual average expenditure per reporting household or an annual proportion of households reporting an expenditure for expenditures collected with short reference periods from reference year 2010 onward. This concept and application of the modelling method are described in Section 5.

For years prior to SHS 2010, the number of households reporting expenses in the reference year is considered valid, since all expenditure categories were collected using a 12-month recall period.

The SHS online data tables for 2010 onward present average expenditures per household. The average expenditure per household is based on all households, including those who did not report a given category of spending. Annual estimates of total expenditure and of average expenditure per household are considered accurate representations of annual spending since the under-estimated and over-estimated annualized values offset each other at the aggregate level. Since the final sample consists of all responding households spread across the 12 monthly sub-samples, estimates of total expenditure and average annual expenditure per household also account for seasonal variations in spending.

3. Description of the SHS modelled annual statistics tables

The SHS modelled annual statistics refer to the modelled average annual expenditure per reporting household and the modelled annual proportion of households reporting for Canada (10 provinces only) for reference years 2010 to 2017^Note . These statistics are available for selected expenditure categories only^Note .

Three tables are included in the appendix of this document, as well as in Microsoft Excel format:

• Table A: Reference periods used to collect expenditures, 2010 to 2017
• Table B: Modelled average annual expenditure per reporting household, 2010 to 2017
• Table C: Modelled annual proportion of households reporting expenditures, 2010 to 2017

Table A shows the reference period used to collect expenditures for each reference year. The modelled average annual expenditure per reporting household and the modelled annual proportion of households reporting expenditures are presented in Table B and Table C respectively. While all estimates in tables B and C are annual, Table A indicates the length of the reference period that was used to collect each expenditure category (the recall period in the interview or the two-week reporting period of the diary). In tables B and C, the column “Estimates are modelled” indicates the expenditure categories for which the average annual expenditure per reporting household and the annual proportion of households reporting are modelled. In cases where the reference period used to collect expenditures is “12 months” or “last payment”^Note  , the model is not needed to produce the annual statistics.

All dollars values in Table B are in current dollars (not adjusted for inflation). This is also the case for official SHS estimates of average expenditure per household published online.

Some of the expenditure category definitions have been slightly adjusted so that the model could be applied (see Section 5.2.3). These adjustments are indicated in footnotes in the tables.

4. Disclaimer

The SHS modelled annual statistics are derived from a statistical model. They should be interpreted with caution and should not be considered official Statistics Canada estimates. They are based on a set of assumptions (see Section 5.1) and are not accompanied by quality indicators.

By definition, the average expenditure per household is the product of the proportion of households reporting an expenditure and the average expenditure per reporting household. However, the product of the modelled proportion of households reporting an expenditure and the modelled average expenditure per reporting household may not be equal to the official average expenditure per household published by Statistics Canada (Table 11-10-0222-01). This can occur in cases where the definition of the expenditure category is adjusted by adding or removing subcategories or the reference period of the expenditure category changed in a post-redesign cycle (see Section 5.2.3). Footnotes are included in each table to identify such adjustments. Other adjustments made to expenditures (see Section 5.2.1 and Section 5.2.2) lead to discrepancies between the product of the two modelled statistics and the official published average per household, but are not indicated in the table.

5. Methodology

5.1 Method for deriving modelled annual statistics

By definition, the overall average annual expenditure per household (hereafter also referred to as “overall average”) is equal to the annual proportion of households reporting an expenditure (hereafter referred to as “proportion of reporting households”) multiplied by the average annual expenditure per reporting household (hereafter referred to as “average per reporting household”):

$${\widehat{p}}_{annual}^{reporting households}\times {\widehat{\overline{x}}}_{annual}^{reporting household}={\widehat{\overline{x}}}_{annual}^{overall}\text{(1)}$$

This relationship shows that, for a given annual overall average, which is observed and assumed valid, there exists a set of possible solutions for the annual proportion of reporting households and the annual average per reporting household.

Using spending on Pet food as an example, Chart 1 illustrates the set of possible solutions for SHS 2009 (before the redesign) and SHS 2010 (after the redesign). The red curve represents the set of possible solutions based on the overall average expenditure per household in 2009 ($178.27), and the green dot on the red curve shows the 2009 estimates for the annual proportion of reporting households and the annual average per reporting household. The black curve represents the set of possible solutions based on the overall average expenditure per household in 2010 ($190.68). Prior to the redesign, the reference period used to collect all expenses was the calendar year. Because of the redesign, the reference period for Pet food was shortened in 2010 to the two-week diary reporting period. The blue dot on the black curve shows the 2010 estimates for the proportion of reporting households and the average per reporting household over the short reference period. The objective of the method is to find more plausible annual estimates for the proportion of reporting households and the average per reporting household, which constitutes a solution that falls on the black curve.

Data table for Chart 1



This is a line graph.

The horizontal axis is the proportion of reporting households, measured in percentage points. The vertical axis is the average expenditure per reporting household, measured in dollars.

There are two curves on the graph: one for 2009 and one for 2010. The 2009 curve (in red) shows the set of possible solutions (combinations of proportion of reporting households and average expenditure per reporting household) for the 2009 overall average expenditure per household (fixed at $178.27). The 2010 curve (in black) shows the set of possible solutions for the 2010 overall average expenditure per household (fixed at $190.68).

The two curves are convex and do not overlap. The 2009 curve is below the 2010 curve.

There is a green dot along the 2009 curve at the 48.08% and $370.78 mark. These were the values of the 2009 estimates (based on the 12-month reference period used to collect expenditures) that resulted in the $178.27 overall average expenditure per household.

There is a blue dot along the 2010 curve at the 28.96% and $658.46 mark. These were the values of the 2010 estimates (based on the 2-week reference period used to collect expenditures) that resulted in the $190.68 overall average expenditure per household.

Data table for chart 1
Table summary
This table displays the results of Data table for chart 1. The information is grouped by Proportion of reporting households (%) (appearing as row headers), Average expenditure per reporting household, 2009 and Average expenditure per reporting household, 2010, calculated using $ units of measure (appearing as column headers).

Proportion of reporting households (%)	Average expenditure per reporting household, 2009	Average expenditure per reporting household, 2010
	$
25.00	713.09	762.72
33.00	594.24	635.60
35.00	509.35	544.80
40.00	445.68	476.70
45.00	396.16	423.73
50.00	356.54	381.36
Note: Since both curves are continuous, this table includes only a sample of data points. Source: Survey of Household Spending.

To derive a more plausible solution, two additional assumptions are made:

1. The annual estimates for the proportions of reporting households are valid for 2009 and years prior.
2. Changes in the consumption behaviours of the population are minimal and gradual from one year to another. This assumption implies that, for two solutions satisfying Equation (1), the one that minimizes the difference to the previous year’s solution is more plausible.

Based on these two assumptions, the solution for 2010 will satisfy Equation (1) and have the closest distance to the 2009 estimates (green dot in Chart 1). Because the proportion of reporting households and the average per reporting household are measured in different scales (proportions and dollars), the measure of the distance is based on ratio changes for both statistics. Specifically, the minimization problem is defined as:

Minimize $\alpha {\left(\ln ({\widehat{p}}_{annual 2010}^{reporting households})-\ln ({\widehat{p}}_{annual 2009}^{reporting households})\right)}^2+$

$${\left(\ln ({\widehat{\overline{x}}}_{annual 2010}^{reporting household})-\ln ({\widehat{\overline{x}}}_{annual 2009}^{reporting household})\right)}^2\text{(2)}$$

with respect to $\left({\widehat{p}}_{annual 2010}^{reporting households},{\widehat{\overline{x}}}_{annual 2010}^{reporting household}\right)$, under the constraint that

$ln ({\widehat{p}}_{annual2010}^{reporting households})+ln ({\widehat{\overline{x}}}_{annual2010}^{reporting household})=ln ({\widehat{\overline{x}}}_{annual2010}^{overall}).$

The solution is given by

$${\widehat{p}}_{annual 2010}^{reporting households}={\widehat{p}}_{annual 2009}^{reporting households}\times {\left({\widehat{\overline{x}}}_{annual 2010}^{overall}/{\widehat{\overline{x}}}_{annual 2009}^{overall}\right)}^{1/\left(\alpha +1\right)}\text{(3)}$$

${\widehat{\overline{x}}}_{annual 2010}^{reporting household}={\widehat{\overline{x}}}_{annual 2009}^{reporting household}\times {\left({\widehat{\overline{x}}}_{annual 2010}^{overall}/{\widehat{\overline{x}}}_{annual 2009}^{overall}\right)}^{\alpha /\left(\alpha +1\right)}\text{(4)}$

The multiplying constant α in Equation (2) reflects the relative contribution of the change in the proportion of reporting households and the change in the average per reporting household to the change in the overall average. If the constant α equals 1, the distance function gives equal penalties on each dimension. If the constant α is greater than 1, the contribution of the change in the average per reporting household is relatively more important. If the constant α is smaller than 1, the contribution of the change in the proportion of reporting households is relatively more important.

The multiplying constant α in Equation (2) can be expressed as

$$\alpha =\ln \left(\frac{{\widehat{\overline{x}}}_{annual 2010}^{reporting household}}{{\widehat{\overline{x}}}_{annual 2009}^{reporting household}}\right)/\ln \left(\frac{{\widehat{p}}_{annual 2010}^{reporting households}}{{\widehat{p}}_{annual 2009}^{reporting households}}\right)\text{(5)}$$

where ${\widehat{\overline{x}}}_{annual 2010}^{reporting household}$ and ${\widehat{p}}_{annual 2010}^{reporting households}$ are not known.

The estimation of α is conducted as follows.

First, the observed proportion of reporting households and the observed average per reporting household over the reference periods are modelled using the following segmented regressions:

$$\widehat{p_t}={\alpha }_1{I}_{t\le 2009}+{\beta }_1{I}_{t\le 2009}\left(t-2010\right)+{\alpha }_2{I}_{t>2009}+{\beta }_2{I}_{t>2009}\left(t-2010\right)+{\epsilon }_t\text{(6)}$$

$$\widehat{{\overline{x}}_t}={\alpha }_1^{*}{I}_{t\le 2009}+{\beta }_1^{*}{I}_{t\le 2009}\left(t-2010\right)+{\alpha }_2^{*}{I}_{t>2009}+{\beta }_2^{*}{I}_{t>2009}\left(t-2010\right)+{\delta }_t\text{(7)}$$

The I’s in Equations (6) and (7) are indicator functions, that are split across the redesign date.

For example, when t = 2004, 2005, …, 2009, Equation (6) is

$$\widehat{p_t}={\alpha }_1+{\beta }_1\left(t-2010\right)+{\epsilon }_t\text{(6a)}$$

And when t = 2010, 2011, …, 2017, it becomes

$$\widehat{p_t}={\alpha }_2+{\beta }_2\left(t-2010\right)+{\epsilon }_t\text{(6b)}$$

Equation (7) behaves in the same manner.

Under the hypothesis that the trend observed prior to 2010 is still in effect in 2010, the respective change ratio of the two dimensions is estimated by

$${\widehat{c}}_1^{*}=\frac{{\widehat{p}}_{2010}/{\widehat{p}}_{2009}}{{\widehat{\overline{x}}}_{2010}/{\widehat{\overline{x}}}_{2009}}=\frac{\left({\widehat{\alpha }}_1\right)/\left({\widehat{\alpha }}_1-{\widehat{\beta }}_1\right)}{\left({\widehat{\alpha }}_1^{*}\right)/\left({\widehat{\alpha }}_1^{*}-{\widehat{\beta }}_1^{*}\right)}\text{(8)}$$

The following equation, derived from Equations (1), (5), and (8), allows to obtain :

$$\widehat{\alpha }=\frac{\left(\ln \left({\widehat{\overline{x}}}_{annual 2010}^{overall}/{\widehat{\overline{x}}}_{annual 2009}^{overall}\right)-\ln \left({\widehat{c}}_1^{*}\right)\right)}{\left(\ln \left({\widehat{\overline{x}}}_{annual 2010}^{overall}/{\widehat{\overline{x}}}_{annual 2009}^{overall}\right)+\ln \left({\widehat{c}}_1^{*}\right)\right)}\text{(9)}$$

Once the annual estimates for the proportions of reporting households and the averages per reporting household are obtained for 2010, a similar approach is applied to obtain the annual estimates for 2011 and following years. However, for these years, it is assumed that the respective change ratios observed over the reference periods used to collect the data are indicative of what to expect at the annual level. This assumption implies that, for 2011, the respective change ratio is estimated by

$${\widehat{c}}_1^{**}=\frac{{\widehat{p}}_{2011}/{\widehat{p}}_{2010}}{{\widehat{\overline{x}}}_{2011}/{\widehat{\overline{x}}}_{2010}}=\frac{\left({\widehat{\alpha }}_2+{\widehat{\beta }}_2\right)/{\widehat{\alpha }}_2}{\left({\widehat{\alpha }}_2^{*}+{\widehat{\beta }}_2^{*}\right)/{\widehat{\alpha }}_2^{*}}\text{(10)}$$

and the value of α is estimated by

$$\widehat{\alpha }=\frac{\left(\ln \left({\widehat{\overline{x}}}_{annual 2011}^{overall}/{\widehat{\overline{x}}}_{annual 2010}^{overall}\right)-\ln \left({\widehat{c}}_1^{**}\right)\right)}{\left(\ln \left({\widehat{\overline{x}}}_{annual 2011}^{overall}/{\widehat{\overline{x}}}_{annual 2010}^{overall}\right)+\ln \left({\widehat{c}}_1^{**}\right)\right)}\text{(11)}$$

Example

The annual estimates for the proportions of reporting households and the averages per reporting household for Pet food are obtained as follows. To obtain the annual estimates for 2010, first, the segmented regressions (Equations (6) and (7)) are applied by using the estimates for the proportions of reporting households and the average per reporting household over the respective reference periods from 2004 to 2017. The estimated segmented regression equations are shown in Figures 2a and 2b. Substituting the estimated parameters from the segmented regressions into Equation (8) yields the value of ${\widehat{c}}_1^{*}$  (0.9706), and substituting the value of ${\widehat{c}}_1^{*}$  and the values of the overall averages for 2009 and 2010 into Equation (9) gives value of $\widehat{\alpha }$  (2.598). Lastly, with the value of $\widehat{\alpha }$, applying Equations (3) and (4) yields the modelled annual estimates for the proportion of reporting households (48.99%) and the average per reporting household ($389.23). Figure 3 illustrates the modelled annual estimates resulting from the method of annualization in comparison with the estimates over the short reference period.

The annual estimates for the subsequent years are obtained by a similar approach. For example, to obtain the annual estimates for 2011, the value of ${\widehat{c}}_1^{**}$  is calculated using Equation (10) with the estimated parameters from the segmented regressions. Then, substituting ${\widehat{c}}_1^{**}$ into Equation (11) gives the value of $\widehat{\alpha }$ . With the value of $\widehat{\alpha }$ and the annual estimates obtained for 2010, applying the minimization process under the constraint that respects the overall average for 2011 yields the annual estimates for 2011. Table 2 presents the annual estimates for the proportions of reporting households and the averages per reporting household in comparison with the estimates over the short reference periods from 2010 to 2017.

Data table for Chart 2a



This is a line graph.

The horizontal axis displays the survey reference years, from 2004 to 2017. The vertical axis is the proportion of reporting households over the reference period used to collect expenditures, measured in percentage points.

There are three curves on the graph.

The first curve shows the proportion of reporting households over the reference period used to collect expenditures (in red). There are two distinct periods for this line: the period before 2010 and the one from 2010 onward. Before 2010, the proportion of reporting households is generally around 50%. From 2010 onward, the proportion of reporting households is around 25% to 30%.

The second curve shows the projected values for 2004 to 2009 (in grey). This is the regression line for the proportion of reporting households for this period, defined by the equation displayed, ${\widehat{p}}_t=0.4839-0.0016(t-2010).$

The third curve shows the projected values for 2010 to 2017 (in yellow). This is the regression line for the proportion of reporting households for this period, defined by the equation displayed, ${\widehat{p}}_t=0.2952-0.00539(t-2010).$

Data table for Chart 2a
Table summary
This table displays the results of Data table for Chart 2a. The information is grouped by Survey reference year (appearing as row headers), Proportion of reporting households over the reference period used to collect expenditures, Projected values for 2004 to 2009 and Projected values for 2010 to 2017 (appearing as column headers).

Survey reference year	Proportion of reporting households over the reference period used to collect expenditures	Projected values for 2004 to 2009	Projected values for 2010 to 2017
	%
2004	48.66	49.35	This is an empty cell
2005	49.10	49.19	This is an empty cell
2006	50.46	49.03	This is an empty cell
2007	48.59	48.87	This is an empty cell
2008	48.81	48.71	This is an empty cell
2009	48.08	48.55	This is an empty cell
2010	28.96	This is an empty cell	29.52
2011	30.13	This is an empty cell	28.98
2012	27.79	This is an empty cell	28.44
2013	28.18	This is an empty cell	27.90
2014	28.03	This is an empty cell	27.36
2015	25.27	This is an empty cell	26.82
2016	26.53	This is an empty cell	26.29
2017	26.16	This is an empty cell	25.75
Source: Survey of Household Spending.

Data table for Chart 2b



This is a line graph.

The horizontal axis displays the survey reference years, from 2004 to 2017. The vertical axis is the average annual expenditure per reporting household over reference period used to collect expenditures, measured in dollars.

There are three curves on the graph.

The first curve is the average annual expenditure per reporting household over the reference period used to collect expenditures (in red). There are two distinct periods for this line: before 2010 and after 2010. Before 2010, the average per reporting household is around $350 to $400. From 2010 onwards, the average per reporting household is around $550 to $800.

The second curve shows the projected values for 2004 to 2009 (in grey). This is the regression line for the average expenditure per reporting household for this period, defined by the equation displayed, ${\widehat{x}}_t=408.8084+10.7213(t-2010).$

The third curve shows the projected values for 2010 to 2017 (in yellow). This is the regression line for the average expenditure per reporting household for this period, defined by the equation displayed, ${\widehat{x}}_t=641.3307+16.0211(t-2010).$

Data table for Chart 2b
Table summary
This table displays the results of Data table for Chart 2b. The information is grouped by Survey reference year (appearing as row headers), Average annual expenditure per reporting household over the reference period used to collect expenditures, Projected values for 2004 to 2009 and Projected values for 2010 to 2017, calculated using $ units of measure (appearing as column headers).

Survey reference year	Average annual expenditure per reporting household over the reference period used to collect expenditures	Projected values for 2004 to 2009	Projected values for 2010 to 2017
	$
2004	336.01	344.48	This is an empty cell
2005	360.28	355.20	This is an empty cell
2006	352.94	365.92	This is an empty cell
2007	393.98	376.64	This is an empty cell
2008	413.73	387.37	This is an empty cell
2009	370.78	398.09	This is an empty cell
2010	658.46	This is an empty cell	641.33
2011	735.65	This is an empty cell	657.35
2012	554.35	This is an empty cell	673.37
2013	656.52	This is an empty cell	689.39
2014	737.30	This is an empty cell	705.42
2015	727.14	This is an empty cell	721.44
2016	767.35	This is an empty cell	737.46
2017	742.48	This is an empty cell	753.48
Source: Survey of Household Spending.

Data table for Chart 3



This is a line graph.

The horizontal axis is the proportion of reporting households, measured in percentage points. The vertical axis is the average expenditure per reporting household, measured in dollars.

There are two curves on the graph: one for 2009 and one for 2010. The 2009 curve (in red) shows the set of possible solutions (combinations of proportion of reporting households and average expenditure per reporting household) for the 2009 overall average expenditure per household (fixed at $178.27). The 2010 curve (in black) shows the set of possible solutions for the 2010 overall average expenditure per household (fixed at $190.68).

The two curves are convex and do not overlap. The 2009 curve is lower than the 2010 curve.

There is a green dot along the 2009 curve at the 48.08% and $370.78 mark. These were the values of the 2009 estimates (based on the 12-month reference period used to collect expenditures) that resulted in the $178.27 overall average expenditure per household.

There is a blue dot along the 2010 curve at the 28.96% and $658.46 mark. These were the values of the 2010 estimates (based on the 2-week reference period used to collect expenditures) that resulted in the $190.68 overall average expenditure per household.

There is also a purple dot along the 2010 curve at the 48.99% and $389.23 mark. These are the modelled values for 2010. The purple dot has similar proportion of reporting households and average per reporting household to the green dot (the 2009 estimate), but at a higher overall average. The green dot on the 2009 curve has an overall average of $178.27, while the purple dot has an overall average of $190.68 (the same as the blue dot).

Data table for chart 3
Table summary
This table displays the results of Data table for chart 3. The information is grouped by Proportion of reporting households (%) (appearing as row headers), Average expenditure per reporting household, 2009 and Average expenditure per reporting household, 2010, calculated using $ units of measure (appearing as column headers).

Proportion of reporting households (%)	Average expenditure per reporting household, 2009	Average expenditure per reporting household, 2010
	$
25	713.09	762.72
33	594.24	635.60
35	509.35	544.80
40	445.68	476.70
45	396.16	423.73
50	356.54	381.36
Note: Since both curves are continuous, this table includes only a sample of data points. Source: Survey of Household Spending.



5.2 Supplementary specifications and adjustments

Before applying the method for deriving modelled annual statistics, some supplementary specifications and adjustments are required, including specifications for mixed expenditure categories, adjustments for aggregate totals, a concordance of the definitions of expenditure variables, and adjustments for inflation.

5.2.1 Specifications for mixed expenditure categories

A mixed expenditure category consists of both a diary-collected component and an interview-collected component. For example, the Pet expenses category is a mixed category since it includes interview-collected expenditures such as Veterinarian and other services, as well as diary-collected expenditures such as Pet food and Purchase of pets and pet-related goods. Since only a proportion of the interviewed households will complete a diary, two different sets of weights are needed to produce estimates: one set for the interview (assigned to all respondents) and the other one for the diary (assigned to respondents that completed both the interview and the diary). Each set of weights independently represents the population of households.

For a given mixed expenditure category, the observed proportion of reporting households and the observed average per reporting household are determined by using the sub-sample of households that completed both the interview and the diary (with the diary weights). The overall average (used as part of the constraint) is calculated by summing up the overall average of the diary-collected component (with the diary weights) and that of the interview-collected component (with the interview weights). This way, the proposed modeled statistics are consistent with the official published average expenditures (unless additional adjustments such as those listed under Section 5.2.2 are required).

5.2.2 Adjustments for aggregate totals

The new reference periods and collection methods introduced with the 2010 redesign could result in a noticeable difference in the estimates of aggregate totals before and after the redesign. To reduce the potential impacts of the redesign on the total estimates, the aggregate totals are adjusted for some expenditure categories before they are used in deriving modelled annual statistics.

To determine if there is a noticeable difference in the level of total estimates before and after the redesign, the totals in the years 2010, 2011, and 2012 are compared to the totals in the years 2009 and 2008. In general, a total may require an adjustment if there are differences of 10% or more. However, an adjustment may not be required if the expenditure was collected using the 12-month or “last payment” reference period and exhibits an increasing or decreasing trend or if the level of expenditure was impacted by the 2008 economic recession. A graphical examination is also applied to determine whether an adjustment on the total is required or not. If an adjustment on the total is not necessary, the method for deriving modelled annual statistics can be applied. If an adjustment on the total is necessary, two cases are treated separately as follows.

a) Reference periods are stable after the redesign

In cases where the length of the reference periods remains the same during the post-redesign period, a linear regression based on the observed totals from 2004 to 2009 is first used to project a value for the 2010 total. Next, the inverse of the ratio of the projected 2010 total to the observed 2010 total is used as a constant multiplier to adjust the 2004-2009 totals. 

Example

Because of the redesign, the reference period for Games of chance switched to the two-week diary reporting period in 2010 and remained stable in following years. Chart 4 shows that the change in the reference period is associated with an important decrease in the observed totals. To adjust the pre-redesign estimates of totals, a linear regression based on the observed 2004-2009 totals is first used to project a value for the 2010 total, which allows to calculate the ratio of the projected 2010 total to the observed 2010 total (2.2329). Next, dividing the observed 2004-2009 totals by the ratio yields the adjusted 2004-2009 totals (Table 3). 

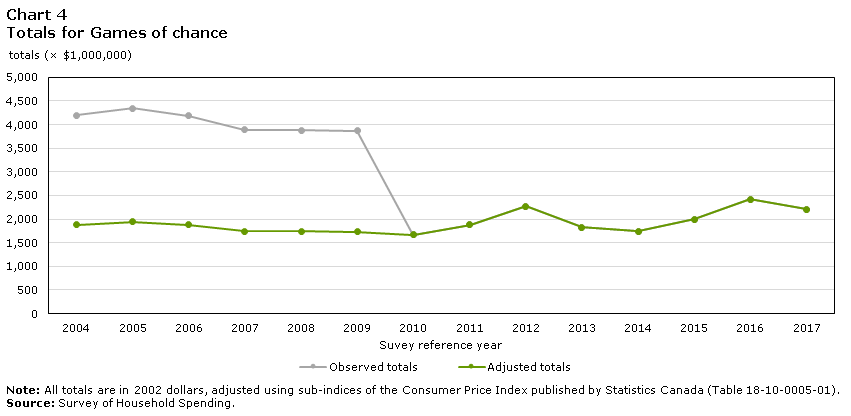
Data table for Chart 4



This is a line graph.

The horizontal axis displays the survey reference years, from 2004 to 2017. The vertical axis displays expenditure totals, measured in millions of dollars.

There are two lines on the graph.

The first line shows the observed totals (in grey). This line has two distinct sections. The first is from 2004 to 2009, when the observed totals are around $4,000 million. In 2010, the line drops to around $1,750 million and remains under $2,500 million from 2010 to 2017.

The second line shows the adjusted totals (in green). From 2004 to 2009, it follows a similar path to the observed totals, but at lower levels (under $2,000 million). From 2010 to 2017, it follows the exact same path as the observed totals.

Data table for Chart 4
Table summary
This table displays the results of Data table for Chart 4. The information is grouped by Survey reference year (appearing as row headers), Observed totals and Adjusted totals, calculated using millions of dollars units of measure (appearing as column headers).

Survey reference year	Observed totals	Adjusted totals
	millions of dollars
2004	4,193	1,878
2005	4,342	1,945
2006	4,186	1,875
2007	3,892	1,743
2008	3,880	1,738
2009	3,865	1,731
2010	1,669	1,669
2011	1,884	1,884
2012	2,268	2,268
2013	1,823	1,823
2014	1,738	1,738
2015	2,000	2,000
2016	2,414	2,414
2017	2,212	2,212
Source: Survey of Household Spending.



b) Reference periods changed in a post-redesign cycle

As the first step in cases where the reference period of the reported expenses changed in a post-redesign cycle t, a linear regression based on the observed totals from t to 2017 is used to project values for the totals from 2010 to t-1. The projected totals obtained in the first step are used as the adjusted totals for 2010 to t-1.  In a second step, a linear regression based on the observed totals from 2004 to 2009 is used to project another value for the 2010 total. Lastly, the inverse of the ratio of the projected 2010 total obtained in the second step to the projected 2010 total obtained in the first step is used as a constant multiplier to adjust the 2004-2009 totals.

Example

In 2010, the reference period for Clothing services was the two-week diary reporting period. From 2011 to 2017, Clothing services was a mixed category consisting of expenses collected through the two-week diary as well as expenses collected through the interview with a three-month recall period. Chart 5 shows that the observed total in 2010 is noticeably lower than those in the other cycles. The first step of the adjustment is to project a value for the 2010 total using a linear regression based on the observed 2011-2017 totals. The second step is to project another value for the 2010 total using a linear regression based on the observed 2004-2009 totals. The ratio of the projected 2010 total obtained in the first step to the projected 2010 total obtained in the second step is 1.0909. Dividing the observed 2004-2009 totals by the ratio yields the adjusted 2004-2009 totals, and the projected 2010 total obtained in the first step is used as the adjusted 2010 total (Table 4).

Data table for Chart 5



This is a line graph.

The horizontal axis displays the survey reference years, from 2004 to 2017. The vertical axis displays expenditure totals, measured in millions of dollars.

There are two lines on the graph.

The first line shows the observed totals (in grey). This line has two distinct sections. The first is from 2004 to 2009, when the totals are within the range of $1,450 million to $1,650 million. In 2010, the line drops down to under $600 million. In 2011, it increases to around $1,400 million. It remains between $1,000 million and $1,400 million from 2011 to 2017.

The second line shows the adjusted totals (in green). From 2004 to 2009, it follows a similar path to the observed totals, but at slightly lower levels (about $200 million lower). In 2010, it does not drop like the line for the observed totals, but instead stays steady. From 2011 to 2017, it follows the exact same path as the observed totals.

Data table for Chart 5
Table summary
This table displays the results of Data table for Chart 5. The information is grouped by Survey reference year (appearing as row headers), Observed totals and Adjusted totals, calculated using millions of dollars units of measure (appearing as column headers).

Survey reference year	Observed totals	Adjusted totals
	millions of dollars
2004	1,511	1,385
2005	1,486	1,363
2006	1,632	1,496
2007	1,527	1,400
2008	1,535	1,407
2009	1,525	1,398
2010	578	1,418
2011	1,384	1,384
2012	1,294	1,294
2013	1,151	1,151
2014	1,302	1,302
2015	1,128	1,128
2016	1,050	1,050
2017	1,024	1,024
Source: Survey of Household Spending.



5.2.3 Concordance of the definitions of expenditure variables

To ensure that the definition of each expenditure category is consistent over time, some expenditure categories are adjusted by adding or removing subcategories. For example, the spending on E-cigarettes and supplies for electronic cigarettes was removed from the spending on Tobacco products and alcoholic beverages because the former was not included in the latter before SHS 2015. Any expenditure categories that were defined differently over time and for which a concordance cannot be re-established by adding or removing subcategories are ineligible are ineligible for the application of the method for deriving modelled annual statistics.

5.2.4 Adjustments for inflation

To remove the influence of inflation on the modelled annual statistics, all expenditure amounts were converted to 2002 dollars before the application of the method using sub-indices of the Consumer Price Index published by Statistics Canada (Table 18-10-0005-01). After the application of the method, all of the modelled annual statistics are converted back to current dollars for the final estimates.

6. References

• Champagne M. 2018. Produire des statistiques annuelles à partir de données rapportées sur de courtes périodes de temps : L’expérience de l’enquête sur les dépenses des ménages. Proceedings of the Survey Methods Section, Statistical Society of Canada Annual Meeting, June 2018.
• User Guide for the Survey of Household Spending, 2017 (62F0026M, no. 1).
• Note to Users of Data from the 2010 Survey of Household Spending (62F0026M, no. 2).

7. Contact us

For questions about this product or for more information about the Survey of Household Spending and other related products and services, contact us (514-283-8300; toll-free 1-800-263-1136; STATCAN.infostats-infostats.STATCAN@canada.ca).

Appendix

Table A: Reference periods used to collect expenditures, 2010 to 2017

Table B: Modelled average annual expenditure per reporting household, 2010 to 2017

Table C: Modelled annual proportion of households reporting expenditures, 2010 to 2017

These tables are also available in Microsoft Excel format.