Economic and Social Reports
Gender differences in STEM enrolment and graduation: What are the roles of academic performance and preparation?
DOI: https://doi.org/10.25318/36280001202101100004-eng
Skip to text
Text begins
Abstract
Despite women outnumbering men in postsecondary institutions, men continue to earn more than women in the labour market. While many factors may explain the gender wage gap, the gap in educational attainment favouring women may offer the potential for future reductions in the wage gap. In this regard, field of study choice is key as earnings tend to vary substantially along this dimension. For example, graduates of science, technology, engineering and mathematics (STEM) programs typically earn more than non-STEM graduates, but women in universities and colleges are considerably less likely than their male counterparts to select STEM fields.
The goal of this study is to estimate gender differences in the probability of enrolling in and graduating from a STEM-related postsecondary program (particularly at the bachelor’s degree level). Results are generated for all high school graduates and the subsample who enrolled in a bachelor’s degree program. Results are also generated based on a traditional definition of STEM and for alternative broad and narrow definitions of STEM. The study relies on enrolment and graduation data from universities and colleges (the Postsecondary Student Information System), and academic performance and preparation data before high school graduation for British Columbia students. The results suggest that among high school graduates, women are 29.8% less likely than men to enrol in a postsecondary STEM program shortly after graduation. The gender gap in STEM enrolment falls to 19.9% when focusing only on bachelor’s degree STEM programs. However, when the subsample of high school graduates who enrolled in a bachelor’s degree program is considered, the gender gap in STEM enrolment is almost twice as large (36.4%). For both the high school graduates and bachelor’s degree student samples, the gender gap in graduation from a bachelor’s degree STEM program is about as large as the gender gap in STEM enrolment. Among bachelor’s degree students, by far the largest gap in STEM enrolment is within engineering programs, while much smaller gaps exist in other math-intensive STEM fields. Female bachelor’s degree graduates are slightly more likely than their male counterparts to enrol in other STEM fields.
Only one-third of the gender gap in STEM enrolment and graduation among bachelor’s degree students can be explained by gender differences in academic performance in STEM-related and non-STEM-related high school subjects, STEM-readiness (denoted by taking at least three Grade 12 STEM-related electives), and neighbourhood and high school characteristics. An even smaller portion of the gender gap in engineering enrolment can be explained by these factors. Gender differences in STEM role models (teachers or parents), as well as interest, confidence, and societal norms, could also play important roles in understanding the gender differences in STEM enrolment and graduation, and could potentially also explain the gender difference in STEM-readiness. Gaining further insights into the gender gap in STEM may require additional data in these areas.
Authors
Ping Ching Winnie Chan, Tomasz Handler and Marc Frenette are with the Social Analysis and Modelling Division, Analytical Studies Branch, at Statistics Canada.
Introduction
Numerous studies have shown that women earn less than men, despite having achieved higher levels of educational attainment (Pelletier, Patterson and Moyser 2019). With so many young women in universities and colleges, there is a real potential for wage parity, but program selection is key (Frenette and Handler 2020). As today’s world becomes increasingly digital, technology plays a greater role in innovation and economic development. Over time, this may result in increasing demand for science-, technology-, engineering- and mathematics- (STEM) based skills in the labour market. To date, graduates of many STEM programs have typically earned more than those of non-STEM programs.Note At the aggregate level, data from the 2016 Census of Population show that full-time, full-year average wages and salaries of STEM bachelor’s degree graduates were about $15,000 higher than those of their non-STEM counterparts ($92,800 versus $78,025) in 2015 (Statistics Canada 2016). Since fewer women than men are graduating from STEM fields (Wall 2019),Note this underrepresentation of women likely contributes to overall gender disparities in labour market outcomes such as employment, job match and earnings (Brown and Corcoran 1997; Beede et al. 2011).
Since the gateway to many STEM jobs is a STEM credential from a postsecondary institution, many studies have examined the persistent underrepresentation of women in STEM programs among postsecondary graduates, as described in the literature review in the next section. The goal of this study is to refine the Canadian evidence regarding the extent to which gender differences in STEM skills before high school graduation explain gender differences in the probability of selecting STEM fields in a bachelor’s degree program. To do so, the study uses an administrative dataset that provides detailed academic performance information on students from kindergarten to Grade 12 in Canada’s third-most populous province, British Columbia.
The study contributes to the literature on the gender gap in STEM in three ways.
First, the study distinguishes between two types of gender differences in the probability of selecting STEM-related fields in a bachelor’s degree program, those that are conditional on enrolment in a bachelor’s degree program and those that are unconditional on doing so. Previous studies focus on conditional gender differences. While such differences are important (as they may point to important gender differences in the choice of field of study once in a bachelor’s degree program), they do not take into account the fact that women are far more likely than men to enrol in a bachelor’s degree program. Thus, the unconditional gender gap in STEM selection is necessarily smaller than the conditional gap, and this provides an alternative perspective on the issue. In this study, both gaps are highlighted and examined.
Second, the study highlights not only the gender differences in STEM versus non-STEM choices, but also gender differences in specific STEM programs. Largely because of sample size limitations, this has not been done in previous Canadian studies. Yet, it is important, as different STEM fields require different sets of skills, and different labour market outcomes are associated with different STEM programs. Moreover, there are significant gender differences in participation across STEM programs, with men more likely to enrol in engineering or computer science, and women more likely to enrol in biology.
Third, the study links the British Columbia data with the Postsecondary Student Information System (PSIS), which covers virtually all transitions into Canada’s public postsecondary institutions. By doing so, the study can follow high school students over time with a great degree of precision, i.e., without suffering from the substantial sample attrition that affects longitudinal household surveys.
This study is organized as follows: Section 2 reviews the literature. The data and methods are discussed in Section 3. Section 4 presents the results. Finally, the conclusion summarizes the study and offers thoughts about future work in the area.
Literature review
A large amount of literature from economics, sociology, psychology and other disciplines has studied the persistent underrepresentation of women in STEM occupations. Focusing mostly on the context of the United States, Kahn and Ginther (2017) summarized this extensive literature on women in STEM fields from childhood, middle and high school, and then to university and additional higher education, and finally into the job market. One key finding of their work was that STEM fields differed, and women’s underrepresentation was mostly found within the mathematics-intensive science fields—geosciences, engineering, economics, math and computer science, and physical science.Note Consistent with Arcidiacono (2004) and Zafar (2013),Note Kahn and Ginther’s review pointed to preferences and psychological explanations for the underrepresentation of women in mathematics-intensive STEM fields. They concluded that most studies found that grades or test scores were correlated with subsequent choices concerning STEM course-taking and field of study selection, but the correlation explained little of the overall gender differences in these outcomes (e.g., Turner and Bowen 1999; Xie and Shauman 2003).
Delaney and Devereux (2019) used unique data on preference rankings for all secondary students who applied for university in Ireland and detailed information on school subjects and grades in the terminal high school exam (Leaving Certificate Examinations) to decompose the sources of the gender gap in STEM college programs. They also found large gender enrolment gaps in engineering and technology, but no gaps in science. The gender gap was smaller when nursing degrees were included in STEM, showing that the results and conclusions can be sensitive to the STEM definition.
More closely related to the current study, Fryer and Levitt (2010) studied a nationally representative cohort of American children who entered kindergarten in 1998 in the Early Childhood Longitudinal Study Kindergarten Cohort and found that boys and girls entered kindergarten with similar average math test scores, but by the spring of their 5th grade year, a gender gap equivalent to 0.2 standard deviations in favour of boys emerged. In addition, boys were more likely than girls to perform in both tails of the mathematics distributions (especially in the right tail), and this may have later given rise to some of the gender differences observed in STEM choice.Note
How do previous grades or test scores correlate with subsequent choices concerning STEM course-taking and postsecondary enrolment decisions? Friedman-Sokuler and Justman (2016) studied Israeli high school STEM elective course choices to examine whether previous grades or test scores correlate with subsequent choices concerning STEM course-taking and majors. They found that the 8th grade standardized test scores had a relatively small effect on the probability of choosing STEM courses. In addition, whether boys or girls were more affected by past performances depended on the subject—girls’ decisions were more sensitive to grades in biology and chemistry, while boys’ decisions were more sensitive to computer science and physics grades.
In addition to the impact of grades or scores in STEM courses, what matters may be the comparative advantage girls and boys might have at the end of secondary schooling, i.e., their STEM ability relative to other abilities. Riegle-Crumb et al. (2012) found that the comparative advantage in STEM ability compared with verbal ability explained more of the college major choice than STEM ability alone. Speer (2017) found that the comparative advantage can explain about 6 of the total 17 percentage point gender gap in the U.S. sample. However, the findings of Delaney and Devereux (2019) suggest that overall achievement and comparative advantage (as measured by the differential achievement across subjects, particularly English and mathematics) are relatively unimportant determinants of the gender gap in STEM.
Can high school mathematics-intensive STEM course-taking alone predict postsecondary STEM enrolment? Gottfried and Bozick (2016) found that students who took courses in applied STEM areas in high school (mostly boys) were more likely to choose an applied STEM major. Jacob et al. (2020) studied how country-specific curriculum requirements in secondary school may have contributed to gendered choices in higher education. They compared variation in the freedom of choice of secondary school subjects across Ireland, Scotland and Germany and found that in all three countries women were less likely to enrol in STEM fields of study, but taking more STEM subjects in high school was predictive of entering related fields within higher education (equally for women and men).
There are also a few relevant papers using Canadian data in this literature. Hango (2013) used the longitudinal data from the Youth in Transition Survey (YITS) matched to the Programme for International Student Assessment and concluded that, although mathematical ability at age 15 was positively correlated with the probability of choosing a STEM program later at university, gender differences in the mathematics performance could explain only a small portion of the gender difference in STEM program selection. Finnie and Childs (2018) used the same data to look at differences in enrolment rates across a broader range of groups (including women and many others) and also found that women were far less likely to enrol in STEM programs, even after accounting for differences in mathematics and science grades in high school. The academic measures available from the British Columbia kindergarten to Grade 12 (BC K–12) data in the current study are broader, as they include course marks in mathematics, science and English (the latter being important for measuring comparative advantage); standardized assessment results in science and English; and STEM-related course selection in Grade 12 (important for entry into STEM programs). Moreover, the current study is based on administrative data, which are less prone to attrition compared with survey data.Note Hango (2013) also profiled differences between men and women among young STEM university graduates (aged 25 to 34 with a STEM degree in 2011) using the 2011 National Household Survey. The findings indicated that men with STEM degrees, which were more concentrated in engineering, had better labour market outcomes compared with their non-STEM counterparts (i.e., lower unemployment rate, higher wages and lower rate of job mismatch). However, the labour market outcomes of women with STEM degrees, which were more concentrated in science and technology, did not clearly differ from those of women with non-STEM degrees. These results are important as they highlight differences in labour market outcomes among specific fields within the broader STEM grouping. Moreover, they underscore the importance of studying the choice of specific STEM fields along the gender dimension (which the current study will undertake).
Using the Ontario Universities’ Application Centre (OUAC) data on high school graduates who registered in an Ontario university between 2005 and 2012 and high school cohort data for Grade 9 students in 2005/2006, Card and Payne (2017) showed that there was a significant gender gap in STEM enrolment in university (30.3% of women and 42.5% of men who enrolled in university registered in a STEM program). However, this gap was not the result of differences in STEM-readiness (defined as the completion of at least three STEM-related classes in the last years of high school). In fact, among high school graduates who applied to an Ontario university through OUAC, 17.9% of girls were STEM-ready—almost as high as their male counterparts (18.8%). Instead, girls were far more likely to go to university than boys (53.5% compared with 32.2%, respectively, among the sample of Ontario university applicants). This resulted in a lower proportion of female university students who were STEM-ready (33.3%) compared with their male counterparts (47.4%). It was this factor—the lower level of STEM-readiness among women who registered in a university program—that was primarily behind the gender gap in STEM enrolment among university students. A crucial difference between the current paper and the Card and Payne (2017) is that the BC K–12 data are linked to the PSIS in the former. This linkage enables the analysis of STEM program selection as a function of high school course selection, grades and standardized assessment scores. Moreover, the data include information on non-applicants. This is an important distinction, as women are considerably more likely to enrol in postsecondary programs, and thus, they may also be more likely to apply. Examining gender differences in STEM enrolment (and graduation) among high school graduates provides a different perspective than one obtained from a sample of postsecondary enrolees.
Finally, Wall (2019) used data from the Education and Labour Market Longitudinal Platform to examine the persistence and representation of women in STEM over the course of an undergraduate degree in Canada.Note The study concluded that women’s lower representation in STEM programs was largely explained by lower enrolments in STEM programs at the start of their postsecondary education, as women’s representation in STEM remained essentially stable over the course of their undergraduate degree. More specifically, the retention of men and women in STEM programs was more or less similar; as a result, the proportion of women among STEM graduates in 2015 was similar to that among first-year STEM students in 2010. The current study also examines graduation from STEM programs, not only on a sample of postsecondary enrolees, but also on a sample of high school graduates.
While women are more likely than men to leave STEM for non-STEM programs, men are more likely to leave STEM for dropping out of their bachelor’s degree program, meaning that men do not move into non-STEM programs to the same extent as women.
The Canadian literature has generally maintained a traditional definition of STEM. The current study will also examine gender differences in the traditional STEM fields. In addition, it will explore alternative definitions of STEM, in recognition of the important gender differences in specific areas of STEM.
Data and methods
The goal of this study is to estimate gender differences in the probability of enrolling in and graduating from a STEM-related postsecondary program (and particularly at the bachelor’s degree level). Results will be generated for all high school graduates and the subsample who enrolled in a bachelor’s degree program. Results will also be generated based on a traditional definition of STEM, and for alternative broad and narrow definitions of STEM.
The results of this study were derived from two data sources that are linked at the individual level, the British Columbia Ministry of Education dataset (BC K–12) and the Postsecondary Student Information System (PSIS).
The BC K–12 dataset provides student-level information for individuals attending British Columbia’s public and independent schools. The data include information about student characteristics (gender, age, geographic location, etc.) and progress through the education system (Foundation Skills Assessment results, provincial exam scores in high school, subject course grades, graduation, etc.). Data are available from 1991 to the present.
The PSIS contains detailed information on all individuals enrolled in all Canadian provincially funded postsecondary institutions, such as enrolment year, registration status in the fall semester (full-time or part-time), program type (level and credential), field of study (2011 Classification of Instructional Programs) and graduation date. Comprehensive enrolment data are available from 2009 onwards, while comprehensive graduation data are available from 2010 onwards.
Through collaborative work with the British Columbia Ministry of Education, Statistics Canada has linked individuals between the BC K–12 and PSIS datasets. This linkage enables the use of longitudinal data to examine the choice of the field of study in a bachelor’s degree program with regard to earlier academic performance measures. In this study, three cohorts of high school graduates in British Columbia are followed: those who were 18 and 19 years old at the time of graduation in 2009, 2010 or 2011.Note These criteria yielded a sample of 56,685 male and 56,411 female high school graduates.
To be included in the bachelor’s degree enrolment sample, the student had to enrol in a bachelor’s degree program in a postsecondary institution (university or college) before the end of the year after their high school graduation. For example, for the 2011 high school graduation cohort, the bachelor’s degree student sample only includes students who were enrolled in a bachelor’s degree program in 2011 or 2012.Note These criteria yielded a sample of 17,851 male and 22,365 female bachelor’s degree students.
The outcomes examined in this study include enrolment in a traditional STEM postsecondary program (certificate, diploma, associate degree or bachelor’s degree), enrolment in a STEM bachelor’s degree program and graduation from a STEM bachelor’s degree program. For the enrolment outcomes, one broad and two narrow definitions of STEM were also included. Broad STEM includes traditional STEM fields and health care fields. The traditional definition of STEM was also disaggregated into two mutually exclusive and exhaustive narrow definitions of STEM. The first is based on math-intensive fields, including computer science, engineering, mathematics, physics, chemistry and other math-intensive fields (e.g., combining any of the above). The second includes STEM fields that are less math-intensive, such as biological sciences and general and integrated sciences. For comparison, results are also shown for non-STEM enrolment, which is split into health care, business and related fields, and other. As noted above, enrolment by the end of the year after high school graduation is examined. A final outcome is graduation from a bachelor’s degree STEM program within six years of high school graduation. Note that enrolment and graduation data from the full PSIS are included in this study (including from institutions outside British Columbia).
These outcomes will be shown separately for men and women. Importantly, the gender differences in the outcomes will also be shown after accounting for gender differences in important determinants of STEM enrolment and graduation in a series of linear probability models.Note These include various measures of academic performance in Grade 10 (quintile indicators of the science provincial exam and course mark, the mathematics course mark, and the English provincial exam and course mark);Note a measure of STEM-readiness (an indicator of having taken at least three of the four Grade 12 STEM-related electives—mathematics, physics, chemistry and biology); neighbourhood characteristics (percentage with at least a bachelor’s degree and average income within the student’s postal code); and fixed effects for the high school, the high school graduation cohort and age at graduation.
Results
The percentage of people who enrolled in or graduated from a traditional STEM program is shown in Chart 1. Beginning with the broadest sample (high school graduates) and all postsecondary STEM programs as the outcome, 12.9% of women enrolled in a STEM program by the end of the year subsequent to high school graduation. In comparison, 18.3% of their male counterparts followed the same path. This difference of 5.5 percentage points corresponds to a 29.8% lower probability of women enrolling in STEM.
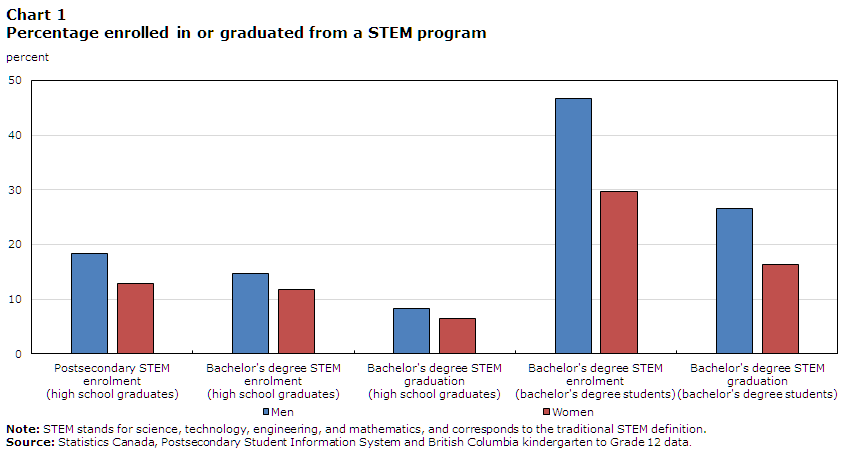
Data table for Chart 1
| Postsecondary STEM enrolment (high school graduates) | Bachelor's degree STEM enrolment (high school graduates) | Bachelor's degree STEM graduation (high school graduates) | Bachelor's degree STEM enrolment (bachelor's degree students) | Bachelor's degree STEM graduation (bachelor's degree students) | |
|---|---|---|---|---|---|
| percent | |||||
| Men | 18.34 | 14.73 | 8.34 | 46.78 | 26.50 |
| Women | 12.87 | 11.80 | 6.49 | 29.76 | 16.38 |
|
Note: STEM stands for science, technology, engineering, and mathematics, and corresponds to the traditional STEM definition. Source: Statistics Canada, Postsecondary Student Information System and British Columbia kindergarten to Grade 12 data. |
|||||
When only bachelor’s degree STEM programs are considered, the gender gap in enrolment narrows, in both absolute and relative terms. Specifically, 14.7% of male high school graduates enrolled in a bachelor’s degree STEM program, compared with 11.8% of female high school graduates (a difference of 2.9 percentage points, or 19.9%).
Of course, the ultimate academic goal of enrolling in a STEM program is to graduate from the program. Chart 1 also shows the percentage of male and female high school graduates who graduated from a bachelor’s degree STEM program within six years of graduating from high school. In this case, the gender gap is even smaller when compared with the gender gap in STEM enrolment. Specifically, 8.3% of male high school graduates completed a bachelor’s degree STEM program, compared with 6.5% of their female counterparts. This gender gap of 1.9 percentage points represents a difference of 22.2%.
The gender gap in STEM enrolment and graduation is substantially smaller among high school graduates than among the narrower sample of bachelor’s degree students. The reason is that female high school graduates are more likely (39.6%) than their male counterparts (31.5%) to enrol in a bachelor’s degree program. This results in increased enrolment (among female high school graduates) in all fields, including those related to STEM.Note
How much of a difference arises by focusing on bachelor’s degree students? The results in Chart 1 suggest that it makes a considerable difference. For example, 46.8% of male bachelor’s degree students enrolled in STEM programs, compared with 29.8% of their female counterparts. This corresponds to a gender gap of 17.0 percentage points, or 36.4% (compared with 19.9% among high school graduates). Similar gender gaps are registered with regard to graduation from a bachelor’s degree STEM program (38.2% among bachelor’s degree students, compared with 22.2% among high school graduates).
The fact that the gender gap in STEM enrolment and graduation is considerably smaller among all high school graduates is noteworthy, as most studies focus on the gender gap among bachelor’s degree students. The decision to focus on the gender gap in STEM among high school graduates or among bachelor’s degree students is important, as the underlying sources of the differences may be very different.
The results in Chart 1 also suggest that gender differences in the field of study chosen by the students who enrolled in a bachelor’s degree program account for roughly twice the overall gender gap in STEM among high school graduates.Note For policy purposes, understanding what is behind those different choices may be of paramount importance given the size of this gap. Thus, the remainder of this study will focus on bachelor’s degree students. A first step towards this goal is to consider alternative definitions of STEM. For example, the broad definition of STEM proposed in this study includes health care fields, since these generally incorporate several science courses as part of their program requirements. Moreover, women are more likely to enrol in these fields than men. Through this broader lens, the gender gap in STEM enrolment is reduced somewhat in comparison with the traditional definition of STEM (Chart 2). When health care fields are added, the percentage of female bachelor’s degree students who enrolled in STEM increases from 29.8% to 35.6%. The same is true for their male counterparts, but to a lesser extent (from 46.8% to 48.8%). This results in a reduction in the gender gap in STEM enrolment from 36.4% (traditional STEM) to 27.0% (traditional STEM plus health care).
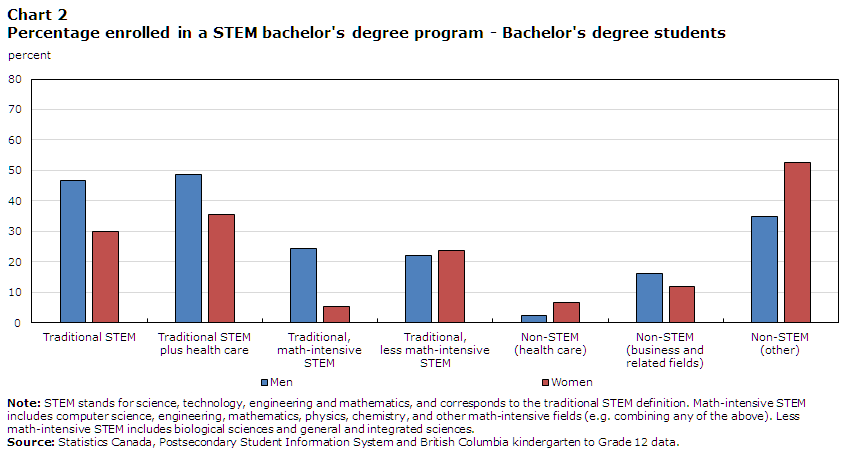
Data table for Chart 2
| Traditional STEM | Traditional STEM plus health care | Traditional, math-intensive STEM | Traditional, less math-intensive STEM | Non-STEM (health care) | Non-STEM (business and related fields) | Non-STEM (other) | |
|---|---|---|---|---|---|---|---|
| percent | |||||||
| Men | 46.78 | 48.78 | 24.19 | 22.16 | 2.43 | 16.28 | 34.94 |
| Women | 29.76 | 35.61 | 5.41 | 23.53 | 6.67 | 11.71 | 52.68 |
|
Note: STEM stands for science, technology, engineering and mathematics, and corresponds to the traditional STEM definition. Math-intensive STEM includes computer science, engineering, mathematics, physics, chemistry, and other math-intensive fields (e.g. combining any of the above). Less math-intensive STEM includes biological sciences and general and integrated sciences. Source: Statistics Canada, Postsecondary Student Information System and British Columbia kindergarten to Grade 12 data. |
|||||||
Traditional STEM enrolment is then disaggregated into two mutually exclusive and exhaustive narrow definitions of STEM: math-intensive fields and less math-intensive fields. For comparison, results are also shown for non-STEM enrolment, which is split into health care, business and related fields (which are associated with relatively high pay; see Frenette and Handler [2020]), and other.
The results indicate that the largest gender gap in STEM enrolment lies within traditional math-intensive fields. Specifically, 24.2% of male bachelor’s degree students enrolled in math-intensive STEM programs, compared with 5.4% of their female counterparts. In contrast, female bachelor’s degree students were slightly more likely than their male counterparts to enrol in less math-intensive STEM programs (23.5% compared with 22.2%), and almost three times more likely than their male counterparts to enrol in health care fields (6.7% compared with 2.4%). Thus, the gender gap in STEM enrolment, whether based on a traditional or broad definition, is entirely explained by the gender gap in enrolment in math-intensive fields. Among non-STEM programs other than health care, female bachelor’s degree students were less likely than their male counterparts to enrol in business and related fields (11.7% compared with 16.3%), but more likely to enrol in other non-STEM programs (52.7% compared with 34.9%).
The main purpose of this paper is to cast light on the role of academic performance and preparation in high school in explaining gender differences in STEM enrolment and graduation among bachelor’s degree students. The BC K–12 data contain course marks and provincial exam results for several mandatory grade subjects. However, entry into a STEM program also requires a certain number of completed STEM-related classes in Grade 12. The BC K–12 data also contain information on these subjects so that the number of completed STEM-related Grade 12 classes can be computed. Chart 3 shows these results for male and female bachelor’s degree students by the various field-of-study groupings. For both genders, at least 80% of STEM enrolees completed three or more STEM-related classes in Grade 12, according to all definitions of STEM. For health care, the percentages are close to 80% (75.3% of men and 67.7% of women completed at least three STEM-related classes in Grade 12). In contrast, about one-third of male and female enrollees in business and related fields completed at least three STEM-related classes in Grade 12, and roughly one-quarter of their counterparts enrolled in other non-STEM programs did the same. These results support the approach taken by Card and Payne (2017), who worked with Ontario data. Thus, the STEM-readiness measure used in the current study will be based on students completing at least three STEM-related classes in Grade 12.Note
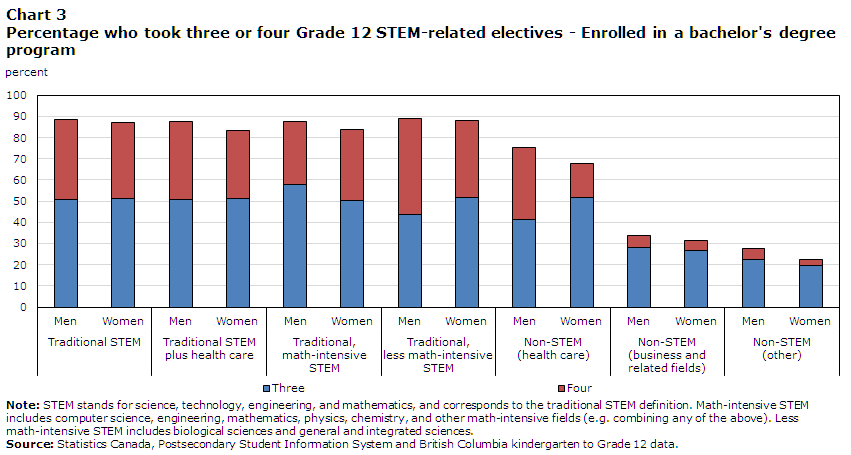
Data table for Chart 3
| Three | Four | |
|---|---|---|
| percent | ||
| Traditional STEM | ||
| Men | 50.96 | 37.37 |
| Women | 51.25 | 35.72 |
| Traditional STEM plus health care | ||
| Men | 50.63 | 37.09 |
| Women | 51.48 | 32.04 |
| Traditional, math-intensive STEM | ||
| Men | 57.76 | 30.01 |
| Women | 50.12 | 33.94 |
| Traditional, less math-intensive STEM | ||
| Men | 43.88 | 45.15 |
| Women | 51.73 | 36.16 |
| Non-STEM (health care) | ||
| Men | 41.24 | 34.10 |
| Women | 51.71 | 15.96 |
| Non-STEM (business and related fields) | ||
| Men | 27.98 | 5.71 |
| Women | 26.76 | 4.77 |
| Non-STEM (other) | ||
| Men | 22.56 | 5.11 |
| Women | 19.77 | 2.84 |
|
Note: STEM stands for science, technology, engineering, and mathematics, and corresponds to the traditional STEM definition. Math-intensive STEM includes computer science, engineering, mathematics, physics, chemistry, and other math-intensive fields. (e.g. combining any of the above). Less math-intensive STEM includes biological sciences and general and integrated sciences. Source: Statistics Canada, Postsecondary Student Information System and British Columbia kindergarten to Grade 12 data. |
||
Descriptive statistics on the main explanatory variables used in this study are shown in Table 1 for male and female bachelor’s degree students. For the most part, men and women performed equally well in Grade 10 STEM-related subjects. For example, 36.6% of men performed in the top quintile (20%) of the Grade 10 science course distribution (which was calculated from the sample of male and female high school graduates), compared with 36.8% of women. Similarly, 33.2% of men landed in the fourth quintile, compared with 33.0% of women. Virtually identical results were achieved by both genders across the Grade 10 mathematics course quintiles. However, men did outperform women in the Grade 10 science provincial exam: 44.7% of men performed in the top quintile compared with 36.9% of women.
Despite the relative gender parity in Grade 10 success in STEM-related subjects (with the exception of the science provincial exam), men were more STEM-ready than women after high school graduation (57.9% and 45.3%, respectively).
By comparison, women outperformed men in the Grade 10 English provincial exam and course by substantial margins. For example, 37.5% of women were in the top quintile of the English provincial exam distribution, compared with 28.1% of men. Similarly, 45.3% of women performed in the top quintile of the English course, compared with 27.3% of men.
The finding that women generally outperformed men in Grade 10 English may be one reason why women were less likely to be STEM-ready based on Grade 12 course completion than men, despite the relative gender parity in the distribution of Grade 10 STEM-related performance. It is possible that women pursued non-STEM-related career paths based in part on their comparative advantage in English, which is a foundational course for many social science, education, arts and humanities programs.
| Men | Women | |
|---|---|---|
| percent | ||
| Science provincial exam quintile | ||
| Bottom | 4.1 | 5.9 |
| Second | 9.1 | 12.0 |
| Third | 15.1 | 17.6 |
| Fourth | 27.0 | 27.6 |
| Top | 44.7 | 36.9 |
| Science course quintile | ||
| Bottom | 3.7 | 3.6 |
| Second | 10.0 | 10.1 |
| Third | 16.4 | 16.6 |
| Fourth | 33.2 | 33.0 |
| Top | 36.6 | 36.8 |
| Mathematics course quintile | ||
| Bottom | 5.9 | 6.0 |
| Second | 10.3 | 10.5 |
| Third | 19.0 | 18.6 |
| Fourth | 25.1 | 24.7 |
| Top | 39.7 | 40.1 |
| English provincial exam quintile | ||
| Bottom | 9.6 | 6.3 |
| Second | 16.1 | 12.6 |
| Third | 18.9 | 15.7 |
| Fourth | 27.3 | 27.8 |
| Top | 28.1 | 37.5 |
| English course quintile | ||
| Bottom | 6.1 | 2.4 |
| Second | 15.7 | 8.3 |
| Third | 20.8 | 15.1 |
| Fourth | 30.1 | 28.8 |
| STEM-ready | 57.9 | 45.3 |
|
Notes: STEM stands for science, technology, engineering, and mathematics, and corresponds to the traditional STEM definition. The quintile distributions are based on the high school graduates sample. Source: Statistics Canada, Postsecondary Student Information System and British Columbia kindergarten to Grade 12 data. |
||
Table 2 displays the percentage of male and female STEM-ready bachelor’s degree students who enrolled in or graduated from a STEM or non-STEM program by different level of academic performance in Grade 10. The results suggest that substantial gender differences in STEM enrolment and graduation remain, even after accounting for gender differences in STEM academic performance and preparation. For example, rates of traditional STEM enrolment, broad STEM enrolment (traditional plus health care) and traditional STEM graduation are still somewhat higher among STEM-ready male bachelor’s degree students in the top of the academic performance distribution in STEM-related subjects compared with their female counterparts. However, the differences are particularly large when the focus shifts to math-intensive STEM enrolment. For example, 24.0% of STEM-ready male bachelor’s degree students in the top quintile of the science provincial exam assessments enrolled in a math-intensive bachelor’s degree STEM program, compared with 6.8% of their female counterparts. Similar findings are evident for students in the top quintile of the science and mathematics course performance distribution. In contrast, female STEM-ready bachelor’s degree students at the top of the distribution in Grade 10 STEM performance were more likely than their male counterparts to enrol in less math-intensive STEM or health care programs.
| Enrolment | Graduation | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditional STEM | Traditional STEM plus health care | Traditional, math-intensive STEM | Traditional, less math-intensive STEM | Non-STEM (health care) | Non-STEM (business and related fields) | Non-STEM (other) | Traditional STEM | |||||||||
| Men | Women | Men | Women | Men | Women | Men | Women | Men | Women | Men | Women | Men | Women | Men | Women | |
| percent | ||||||||||||||||
| Science provincial exam quintile | ||||||||||||||||
| Bottom | 0.6 | 0.7 | 0.6 | 0.9 | 0.3 | 0.1 | 0.3 | 0.6 | 0.0 | 0.2 | 0.2 | 0.1 | 0.5 | 0.6 | 0.1 | 0.1 |
| Second | 2.5 | 2.1 | 2.7 | 2.8 | 1.2 | 0.3 | 1.3 | 1.7 | 0.2 | 0.8 | 0.6 | 0.5 | 1.0 | 1.7 | 0.7 | 0.6 |
| Third | 6.2 | 5.6 | 6.5 | 7.0 | 2.7 | 0.7 | 3.4 | 4.6 | 0.5 | 1.6 | 1.1 | 1.0 | 2.5 | 4.2 | 2.4 | 2.1 |
| Fourth | 17.6 | 14.4 | 18.2 | 17.2 | 8.5 | 2.2 | 8.9 | 11.9 | 0.8 | 3.1 | 2.7 | 2.0 | 5.6 | 8.8 | 8.9 | 7.2 |
| Top | 44.5 | 34.3 | 45.7 | 37.7 | 24.0 | 6.8 | 20.1 | 26.8 | 1.6 | 4.2 | 4.9 | 4.4 | 6.9 | 11.0 | 28.9 | 21.9 |
| Science course quintile | ||||||||||||||||
| Bottom | 0.4 | 0.2 | 0.4 | 0.2 | 0.2 | 0.0 | 0.2 | 0.1 | 0.0 | 0.1 | 0.1 | 0.1 | 0.3 | 0.2 | 0.1 | 0.0 |
| Second | 2.4 | 1.1 | 2.5 | 1.5 | 1.2 | 0.2 | 1.2 | 0.9 | 0.1 | 0.4 | 0.6 | 0.3 | 1.4 | 1.3 | 0.7 | 0.3 |
| Third | 6.4 | 3.8 | 6.8 | 4.9 | 3.1 | 0.5 | 3.2 | 3.3 | 0.4 | 1.2 | 1.3 | 0.8 | 3.1 | 3.7 | 2.5 | 1.3 |
| Fourth | 23.1 | 16.2 | 24.0 | 19.5 | 11.8 | 2.5 | 11.1 | 13.3 | 1.1 | 3.7 | 3.4 | 2.5 | 6.5 | 10.3 | 11.9 | 7.7 |
| Top | 39.0 | 35.7 | 40.1 | 39.4 | 20.3 | 6.9 | 18.3 | 28.0 | 1.5 | 4.5 | 4.1 | 4.3 | 5.4 | 10.8 | 25.9 | 22.5 |
| Mathematics course quintile | ||||||||||||||||
| Bottom | 0.6 | 0.3 | 0.6 | 0.4 | 0.2 | 0.0 | 0.4 | 0.3 | 0.0 | 0.1 | 0.2 | 0.0 | 0.4 | 0.4 | 0.2 | 0.0 |
| Second | 2.5 | 1.4 | 2.7 | 1.9 | 0.9 | 0.1 | 1.6 | 1.3 | 0.2 | 0.5 | 0.5 | 0.3 | 1.4 | 1.5 | 0.8 | 0.4 |
| Third | 8.7 | 4.8 | 9.1 | 6.2 | 3.7 | 0.5 | 5.0 | 4.2 | 0.5 | 1.5 | 1.4 | 0.9 | 3.5 | 4.4 | 3.4 | 1.9 |
| Fourth | 17.8 | 12.9 | 18.6 | 15.7 | 8.4 | 1.5 | 9.3 | 11.0 | 0.9 | 3.1 | 2.5 | 1.6 | 5.4 | 7.7 | 9.2 | 6.0 |
| Top | 41.7 | 37.6 | 42.9 | 41.5 | 23.6 | 7.9 | 17.8 | 28.8 | 1.5 | 4.8 | 4.9 | 5.3 | 6.0 | 12.3 | 27.4 | 23.5 |
| English provincial exam quintile | ||||||||||||||||
| Bottom | 5.5 | 2.3 | 5.7 | 2.8 | 3.4 | 0.7 | 2.0 | 1.6 | 0.2 | 0.5 | 1.0 | 0.6 | 1.9 | 1.8 | 2.6 | 1.1 |
| Second | 10.2 | 5.7 | 10.6 | 6.7 | 5.3 | 1.2 | 4.7 | 4.3 | 0.6 | 1.2 | 1.5 | 1.1 | 2.7 | 3.3 | 4.9 | 2.9 |
| Third | 13.0 | 7.6 | 13.6 | 9.1 | 6.8 | 1.3 | 6.1 | 6.2 | 0.7 | 1.6 | 1.7 | 1.4 | 3.1 | 4.0 | 7.2 | 3.8 |
| Fourth | 20.5 | 16.2 | 21.1 | 18.7 | 10.1 | 2.6 | 10.2 | 13.1 | 0.8 | 2.9 | 2.7 | 2.4 | 4.4 | 7.1 | 12.0 | 9.2 |
| Top | 22.2 | 25.2 | 22.9 | 28.3 | 10.9 | 4.2 | 11.0 | 20.3 | 0.9 | 3.8 | 2.6 | 2.7 | 4.5 | 10.0 | 14.3 | 14.9 |
| English course quintile | ||||||||||||||||
| Bottom | 2.6 | 0.4 | 2.7 | 0.6 | 1.5 | 0.2 | 1.1 | 0.3 | 0.1 | 0.1 | 0.4 | 0.1 | 1.1 | 0.5 | 1.0 | 0.1 |
| Second | 7.9 | 2.2 | 8.2 | 2.6 | 4.6 | 0.6 | 3.3 | 1.6 | 0.4 | 0.5 | 1.4 | 0.5 | 2.7 | 1.9 | 3.4 | 0.9 |
| Third | 13.4 | 5.5 | 13.9 | 6.7 | 7.1 | 1.2 | 6.2 | 4.3 | 0.6 | 1.2 | 2.1 | 1.3 | 3.7 | 3.9 | 6.7 | 2.9 |
| Fourth | 23.2 | 15.2 | 24.0 | 17.8 | 11.8 | 2.6 | 11.2 | 12.3 | 1.1 | 2.9 | 3.1 | 2.5 | 5.0 | 7.7 | 13.9 | 8.4 |
| Top | 24.2 | 33.7 | 25.0 | 37.9 | 11.7 | 5.5 | 12.2 | 27.2 | 1.0 | 5.2 | 2.6 | 3.7 | 4.2 | 12.1 | 16.1 | 19.6 |
|
Notes: STEM stands for science, technology, engineering, and mathematics, and corresponds to the traditional STEM definition. Math-intensive STEM includes computer science, engineering, mathematics, physics, chemistry, and other math-intensive fields (e.g., combining any of the above). Less math-intensive STEM includes biological sciences and general and integrated sciences. The quintile distributions are based on the high school graduates sample. Source: Statistics Canada, Postsecondary Student Information System and British Columbia kindergarten to Grade 12 data. |
||||||||||||||||
As mentioned above, the comparative advantage held by women in English could be partially responsible for the remaining gender differences in STEM enrolment and graduation. For this reason, it is important to account for gender differences in as many determinants of STEM enrolment and graduation as possible. To this end, results from multivariate models are shown in Table 3. In each case, a binary variable indicating enrolment in or graduation from a specific field-of-study grouping is regressed on a female binary variable, along with the following covariates: various measures of academic performance in Grade 10 (quintile indicators of the science provincial exam and course mark, the mathematics course mark, and the English provincial exam and course mark); a measure of STEM-readiness (an indicator of having taken at least three of the four Grade 12 STEM-related electives—mathematics, physics, chemistry and biology); neighbourhood characteristics (percentage with at least a bachelor’s degree and average income within the student’s postal code); and fixed effects for the high school, the high school graduation cohort and age at graduation.
| Enrolment | Graduation | |||||||
|---|---|---|---|---|---|---|---|---|
| Model 1: No covariates | Model 2: Covariates added | Model 1: No covariates | Model 2: Covariates added | |||||
| coefficient | standard error | coefficient | standard error | coefficient | standard error | coefficient | standard error | |
| STEM | ||||||||
| Traditional | -0.170Note *** | 0.005 | -0.104Note *** | 0.004 | -0.101Note *** | 0.004 | -0.071Note *** | 0.004 |
| Traditional plus health care | -0.132Note *** | 0.005 | -0.062Note *** | 0.004 | -0.046Note *** | 0.004 | -0.011Note ** | 0.004 |
| Traditional, math-intensive | -0.188Note *** | 0.003 | -0.160Note *** | 0.003 | -0.120Note *** | 0.003 | -0.105Note *** | 0.003 |
| Computer science | -0.032Note *** | 0.002 | -0.028Note *** | 0.002 | -0.019Note *** | 0.001 | -0.016Note *** | 0.001 |
| Engineering | -0.115Note *** | 0.002 | -0.100Note *** | 0.003 | -0.085Note *** | 0.002 | -0.077Note *** | 0.002 |
| Mathematics | -0.007Note *** | 0.001 | -0.004Note *** | 0.001 | -0.006Note *** | 0.001 | -0.004Note *** | 0.001 |
| Physics | -0.007Note *** | 0.001 | -0.006Note *** | 0.001 | -0.004Note *** | 0.001 | -0.004Note *** | 0.001 |
| Chemistry | -0.006Note *** | 0.001 | -0.003Note ** | 0.001 | -0.003Note ** | 0.001 | -0.002Table 3 Note † | 0.001 |
| Other | -0.022Note *** | 0.001 | -0.018Note *** | 0.001 | -0.003Note *** | 0.001 | -0.003Note *** | 0.001 |
| Traditional, less math-intensive | 0.014Note ** | 0.004 | 0.052Note *** | 0.004 | 0.018Note *** | 0.003 | 0.034Note *** | 0.003 |
| Non-STEM | ||||||||
| Health care | 0.042Note *** | 0.002 | 0.047Note *** | 0.002 | 0.056Note *** | 0.002 | 0.060Note *** | 0.002 |
| Business and related fields | -0.046Note *** | 0.003 | -0.054Note *** | 0.004 | -0.019Note *** | 0.003 | -0.028Note *** | 0.003 |
| Other | 0.177Note *** | 0.005 | 0.116Note *** | 0.005 | 0.160Note *** | 0.004 | 0.116Note *** | 0.005 |
Source: Statistics Canada, Postsecondary Student Information System and British Columbia kindergarten to Grade 12 data. |
||||||||
The results suggest that statistically and empirically significant gender differences in STEM enrolment and graduation remain after accounting for the full set of relevant variables available in the data. For example, the unadjusted gender gap in traditional STEM enrolment is 17.0 percentage points (Model 1). After the covariates are included in the model, the gender gap falls to 10.4 percentage points. Thus, only about one-third of the gender gap in STEM enrolment can be explained by gender differences in academic performance and preparation, neighbourhood and high school characteristics, and cohort and age at graduation. Of all these factors, academic preparation (STEM-readiness) varies the most by gender.Note Based on the broad STEM definition (traditional STEM plus health care), the explanatory power of the model is somewhat larger. Specifically, slightly more than half of the unadjusted gender gap in broad STEM enrolment can be explained by gender differences in the covariates. Interestingly, very little of the large gender gap in math-intensive enrolment (18.8 percentage points) can be explained by the covariates in the model, as the gap falls only to 16.0 percentage points after their inclusion. In other words, about 85% of the gender gap in math-intensive STEM enrolment among bachelor’s degree students cannot be explained by factors captured in the available data. In contrast, the small gender gaps in less math-intensive STEM fields and health care, both in favour of women, widen moderately after accounting for differences in academic performance, STEM-readiness and other factors.
The largely unexplained gender gap in math-intensive STEM programs warrants further investigation. In Table 3, this category is also broken down into its constituent parts. By far the largest gender gap in enrolment rates, with or without covariates, is observed in engineering. The gap is 11.5 percentage points before accounting for differences in the available covariates, and 11.0 percentage points after accounting for those differences. The next largest gap is in computer science (about 3 percentage points, with or without covariate adjustments). The gender gaps in mathematics, physics and chemistry enrolment are much smaller (below 1 percentage point in each case).
Generally, the gender gap in STEM graduation is somewhat smaller than the gender gap in STEM enrolment. It is also the case that the graduation gap in STEM remains largely unexplained after including covariates in the model. Moreover, the largest gender gap in STEM graduation is in math-intensive programs (particularly engineering).
Thus, large portions of the gender gaps in STEM enrolment and graduation remain unexplained, despite the richness of the BC K–12 data. This is also the case in engineering, where the largest gaps exist. This points to the possibility of other factors playing important roles. While it is not known what these factors are, there are several potential candidates. For example, role models may matter both at home and in school. The occupation of the mother may play an important role, as it could potentially provide daughters with the information, interest and confidence required to pursue a specific career (e.g., in STEM). The same argument can be made for teachers—being introduced to STEM-related subjects in high school by a female teacher may motivate girls to pursue studies in STEM.Note Such hypotheses could be tested with indicators of the occupation of the mother and the father and the gender of the teachers in specific high school classes. Currently, such information is not available.Note Note For engineering more specifically, one possibility might also be a lack of interest among women to work where engineers are employed—specifically in construction or mining, two industries that are very male-dominated in general (not just among engineers).
Conclusion
The gender gap in STEM fields is important given the opportunities for career advancement associated with STEM. The goal of this study was to better understand gender differences in STEM enrolment based on newly available data from British Columbia high schools and from Canadian postsecondary institutions.
The results suggest that among high school graduates, women are 29.8% less likely than men to enrol in a postsecondary STEM program shortly after graduation. The gender gap in STEM enrolment falls to 19.9% when focusing only on bachelor’s degree STEM programs. However, when the subsample of high school graduates who enrolled in a bachelor’s degree program is considered, the gender gap in STEM enrolment is almost twice as large (36.4%). For both the high school graduates and bachelor’s degree student samples, the gender gap in graduation from a bachelor’s degree STEM program is about as large as the gender gap in STEM enrolment. Among bachelor’s degree students, by far the largest gap in STEM enrolment is within engineering programs, while much smaller gaps exist in other math-intensive STEM fields. Female bachelor’s degree graduates are slightly more likely to enrol in other STEM fields than their male counterparts.
Only one-third of the gender gap in STEM enrolment and graduation among bachelor’s degree students can be explained by gender differences in academic performance in STEM-related and non-STEM-related high school subjects, STEM-readiness (denoted by taking at least three Grade 12 STEM-related electives), and neighbourhood and high school characteristics. An even smaller portion of the gender gap in engineering enrolment can be explained by these factors. Gender differences in STEM role models (teachers or parents), as well as interest, confidence and societal norms, could also play important roles in understanding the gender differences in STEM enrolment and graduation, and could potentially also explain the gender difference in STEM-readiness. Gaining further insights into the gender gap in STEM may require more data in these areas.
References
Akerlof, G.A., and R.E. Kranton. 2000. “Economics and identity.” Quarterly Journal of Economics 115 (3): 715–753.
Arcidiacono, P. 2004. “Ability sorting and the returns to college major.” Journal of Econometrics 121 (1–2): 343–375.
Beede, D.N., T.A. Julian, D. Langdon, G. McKittrick, B. Khan, and M.E. Doms. 2011. Women in STEM: A Gender Gap to Innovation. Economics and Statistics Administrative Issue Brief no. 04-11. Available at: SSRN: https://ssrn.com/abstract=1964782.
Bertrand, M. 2011. “New perspectives on gender.” In Handbook of Labor Economics Volume 4B, ed. O. Ashenfelter and D. Card, chapter 17, p. 1543–1590. Amsterdam: Elsevier.
Brown, C., and M. Corcoran. 1997. “Sex-based differences in school content and the male-female wage gap.” Journal of Labor Economics 15 (3): 431–465.
Card, D., and A.A. Payne. 2017. High School Choice and the Gender Gap in STEM. NBER Working Paper Series, no. 23769. Cambridge, Massachusetts: National Bureau of Economic Research.
Ceci, S.J., D.K. Ginther, S. Kahn, and W.M. Williams. 2014. “Women in academic science: A changing landscape.” Psychological Science in the Public Interest 15 (3): 75–141.
Delaney, J.M., and P.J. Devereux. 2019. It’s Not Just for Boys! Understanding Gender Differences in STEM. IZA Discussion Paper no. 12176.
Finnie, R., and S. Childs. 2018. “Who goes into STEM disciplines? Evidence from the Youth in Transition Survey.” Canadian Public Policy 44 (S1): S43–S55.
Fortin, N. 2005. “Gender role attitudes and the labour-market outcomes of women across OECD countries.” Oxford Review of Economic Policy 21 (3): 416–438.
Frenette, M., and T. Handler. 2020. Which Bachelor’s Degree Programs Were Associated with the Highest Pay Prior to the COVID-19 Pandemic? A Focus on Very Detailed Fields of Study. Economic Insights, no. 120. Statistics Canada Catalogue no. 11-626-X. Ottawa: Statistics Canada.
Friedman-Sokuler, N., and M. Justman. 2016. “Gender streaming and prior achievement in high school science and mathematics.” Economics of Education Review 53: 230–253.
Fryer, R.G., Jr., and S.D. Levitt. 2010. “An empirical analysis of the gender gap in mathematics.” American Economic Journal: Applied Economics 2 (2): 210–240.
Gottfried, M.A., and R. Bozick. 2016. “Supporting the STEM pipeline: Linking applied STEM course-taking in high school to declaring a STEM major in college.” Education Finance and Policy 11 (2): 177–202.
Hango, D. 2013. Gender Differences in Science, Technology, Engineering, Mathematics and Computer Science (STEM) Programs at University. Insights on Canadian Society. Statistics Canada Catalogue no. 75-006-X. Ottawa: Statistics Canada.
Hoffman, F., and P. Oreopoulos. 2009. “A professor like me: The influence of instructor gender on college achievement.” The Journal of Human Resources 44 (2): 479–494.
Jacob, M., C. Iannelli, A. Duta, and E. Smyth. 2020. “Secondary school subjects and gendered STEM enrollment in higher education in Germany, Ireland and Scotland.” International Journal of Comparative Sociology. Available at: https://doi.org/10.1177/0020715220913043.
Kahn, S., and D.K. Ginther. 2017. “Women and STEM.” In The Oxford Handbook on the Economics of Women, ed. S.L. Averett, L.M. Argys, and S.D. Hoffman. New York: Oxford University Press.
O’Grady, K., M.-A. Deussing, T. Scerbina, V. Tao, K. Fung, V. Elez, and J. Monk. 2019. Measuring Up: Canadian Results of the OECD PISA 2018 Study. Toronto: The Council of Ministers of Education of Canada.
Pelletier, R., M. Patterson, and M. Moyser. 2019. The Gender Wage Gap in Canada: 1998 to 2018. Labour Statistics: Research Papers. Statistics Canada Catalogue no. 75-004-M. Ottawa: Statistics Canada.
Riegle-Crumb, C., B. King, E. Grodsky, and C. Muller. 2012. “The more things change, the more they stay the same? Prior achievement fails to explain gender inequality in entry into STEM college majors over time.” American Educational Research Journal 49 (6): 1048–1073.
Speer, J.D. 2017. “The gender gap in college major: Revisiting the role of pre-college factors.” Labour Economics 44: 69–88.
Statistics Canada. 2016. 2016 Census of Population. Statistics Canada Catalogue no. 98-400-X. Ottawa: Statistics Canada
Turner, S.E., and W.G. Bowen. 1999. “Choice of major: The changing (unchanging) gender gap.” Industrial and Labor Relations Review 52 (2): 289–313.
Wall, K. 2019. Persistence and Representation of Women in STEM Programs. Insights on Canadian Society. Statistics Canada Catalogue no. 75-006-X. Ottawa: Statistics Canada.
Xie, Y., and K.A. Shauman. 2003. Women in Science: Career Processes and Outcomes. Cambridge, Massachusetts: Harvard University Press.
Zafar, B. 2013. “College major choice and the gender gap.” Journal of Human Resources 48 (3): 545–595.
- Date modified: