Main article
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
- Introduction
- Literature review
- Data
- Earnings differences across the urban–rural spectrum
- Multivariate analysis
- Conclusion
- References
1 Introduction
Traditionally, analyses of regional earnings differences in Canada have focused on the variability in the earnings of employed workers across provinces. Although the gap in earnings across provinces can be quite large, it is often smaller than the gap across urban–rural areas, with urbanized areas having generally higher earnings than rural areas and larger urban areas having generally higher earnings than smaller urban areas (Beckstead and Brown 2005). 1 Indeed, the variation in earnings across urban–rural areas account for a large part of the variation in provincial earnings. In general, provinces whose populations are concentrated in smaller urban and rural areas have much lower earnings.
Urban–rural earnings differences are not limited to Canada. Evidence from the United States and France suggests a strong positive association between the size of a geographical unit—as measured by population or employment—and earnings. Glaeser and Maré (2001) find workers in large metropolitan areas in the United States earn 33% more than their non-urban counterparts. Yankow(2006) finds a 21% wage premium for workers in cities with a population greater than 250,000 compared with workers found in smaller cities and rural areas. Utilizing data from France, Combes, Duranton and Gobillon (2008) find a positive association between the size of local labour market areas and earnings. Doubling the level of employment in an area increases earnings by about 5%.
Given the magnitude of urban–rural earnings differences in Canada and elsewhere, the objective of this paper is to develop a better understanding of the factors that underlie these differences. In the broadest terms, earnings are likely to increase with the size of metropolitan area because firms in larger urban areas are more productive, allowing them to pay higher wages, and/or the average skill level of workers—their human capital—is higher.
It has long been argued that larger cities provide firms with a productive advantage that is not available to the same extent in smaller cities and rural areas. These agglomeration economies stem from numerous sources, including the better matching of worker skills with firms' needs, access to shared infrastructure (e.g., airports) and knowledge that percolates more effectively among firms in close proximity to each other.
In contrast to agglomeration economies, relatively little attention has been paid to the role of human capital as a driver of urban–rural earnings differences (see Combes, Duranton and Gobillon 2008 and Yankow 2006). Yet, one of the distinguishing characteristics of larger cities is their highly educated populations. For instance, in metropolitan areas with a population greater that 500,000, about one quarter, or 25%, of employed workers have a university degree, while in rural areas this proportion falls to one tenth (2001 Census of Population).
The overarching purpose of this paper is to begin to disentangle the effects of agglomeration economies and skill composition on urban–rural earnings differences. If agglomeration economies are the primary force underlying earnings differences, then these differences are associated with the productive advantages that firms derive from the geographic concentration of economic activity. It is the very nature of urban economies themselves—the dense intertwining of firms and workers—that leads to their advantage. But, if it is the skill composition of cities that matters, then the advantage of cities turns on their capacity to educate, as well as attract and retain, highly skilled workers.
The remainder of the paper is organized as follows. Section 2 provides a brief review of the current literature. Section 3 describes the data used and the classification of urban–rural areas. Section 4 develops a descriptive analysis that anticipates some of the findings that follow from the multivariate analysis presented in Section 5. Section 6 concludes the paper.
2 Literature review
As has been already noted, average earnings tend to differ across urban and rural areas, either because the skill composition of the workforce also differs and/or the average level of productivity of firms varies systematically with location. To understand more fully why human capital composition and productivity vary with location we have to draw on two strands of the literature.
The first strand focuses on why firm-level productivity might vary with location in general and city size in particular. As noted by Combes, Duranton and Gobillon (2008), there are two standard explanations for why productivity varies across geographic units. The first posits that variation in earnings may be related to differences in local 'non-human' endowments that provide firms with a productive advantage. These endowments can include natural features, such as climate or access to natural resources, and/or long-lived investments in infrastructure, public and private institutions and technology.
The second explanation is based on the premise that higher earnings may result from productivity gains tied to the localized interactions of workers and firms. These agglomeration economies may result from either the geographic concentration of activity in general—urbanization economies—or concentration at the industry level—localization economies. Urbanization economies may result from the transfer of knowledge across industries, facilitated by geographic proximity (Jacobs 1969) or efficiency gains associated with the sharing of public goods—e.g., public infrastructure. In this sense, the size of the geographic area may also be capturing endowment effects.
Localization economies, as identified by Marshall (1890), result from the better matching between workers skills and firm needs, a matching that takes place more effectively in larger labour markets (Helsley and Strange 1990; Andersson, Burgess and Lane 2007). The concentration of an industry in a local area may also stimulate the development of input suppliers, resulting in better access to intermediate inputs tailored to the needs of local firms. Finally, non-market interactions facilitated by the concentration of workers in the same industry, such as technological spillovers, may lead to productivity advances and higher earnings. There is growing evidence, based on micro-level plant data, that suggests these localization economies are present (Henderson 2003; Baldwin et al. 2007; Baldwin, Brown and Rigby 2008). 2
In addition to the effects of endowments and agglomeration economies, the composition of firms may also influence workers' wages. In particular, firm size 3 is associated with productivity and wage levels (Idson and Oi 1999). 4 If the size of firms varies systematically with city size, then part of the variation we observe in earnings across cities may be due to the composition of firms rather than agglomeration economies in general, and localization economies in particular.
There is also a growing body of evidence that points to positive relationships between establishment size and the size of an industry in a city, or the size of a city itself. Holmes and Stevens (2002) and Wheeler (2006) find a positive association between the concentration or size of an industry in a geographic area—city, county or region—and the size of its establishments. Holmes and Stevens (2002) also find a positive association between plant size and city size across a broad spectrum of industries. The major exception to this relationship is manufacturing, which follows the opposite pattern.
The obvious implication of this empirical work is that higher earnings associated with the concentration of economic activity in cities may be, in part, due to the industrial organization of production. Wheeler (2006) decomposes the effects of localization economies and industrial organization. He finds that the earnings premium associated with local industry employment levels is more strongly associated with plant size—industrial organization—than the total number of plants—localization economies. As a result, he argues localization economies may be more strongly related to industrial organization than external economies that raise productivity via the usual Marshallian mechanisms.
The second strand of the literature emphasises human capital as a key driver of earnings differences. Both Combes, Duranton and Gobillon (2008) and Yankow (2006) illustrate that observed and unobserved worker skills underlie the variation in earnings across geographic units. For France, Combes, Duranton and Gobillon (2008) find that between 40% and 50% of wage differences across geographic units can be accounted for by differences in the skill composition of their employed workforces. Yankow finds upward of two-thirds of the wage premium enjoyed by larger urban centres—metropolitan areas with a population greater than 1 million—is due to skill and ability composition.
Why workers with favourable workforce characteristics concentrate in larger urban centres is an open question. On the labour-supply side, the most likely explanation draws on the premise that larger labour markets are more effective at matching the skills of workers with the skill requirements of firms, resulting in higher returns to investments in human capital. These higher returns can act both as an incentive for workers with higher skill levels to migrate to larger urban centres—a sorting effect—and, for workers who spent their formative years in larger cities, to invest in human capital—an in situ effect. The increasing numbers of couples where both partners have a profession further exacerbate the matching problem, reinforcing the incentive to locate in large cities (Costa and Khan 2000). On the demand side, Combes, Duranton and Gobillon (2008) argue that workers with higher skills may be attracted to particular locations because of differences in industrial structure, with some locations being favoured by industries that demand higher skills.
There are also other explanations. More highly skilled workers may also be attracted to locations with better amenities, again leading to the concentration of workers with higher skills in particular locations (Florida 2003, 2002; Adamson, Clark and Partridge 2004; Beckstead, Brown and Gellatly 2008).
In summary, there are reasons to believe earnings differences are due to both the uneven distribution of worker skills and abilities across space, and a systematic variation in the productivity of firms that may be related to endowments, agglomeration economies and/or industrial organization.
3 Data
The data for this analysis are derived primarily from the 2001 Census of Population, which provides extensive information on the levels and sources of earnings for Canadians. From the perspective of this study, using the census has both advantages and disadvantages. The advantage of using the census is that it provides detailed information on those characteristics of individuals that are thought to influence earnings levels, such as education, job experience and immigration status. This allows us to link location and personal characteristics with earnings. Our analysis is hampered by the fact that the census is not a longitudinal panel and therefore we are unable to control for unobserved characteristics of individuals that influence earnings levels.
The 2001 detailed (2B) census file is based on a one-in-five sample of the Canadian population and it has approximately 6.08 million observations. For the purposes of this paper, only persons who were employed during the census reference week in 2001 and also employed in 2000 were selected. The sample was restricted in this way to identify the annual number of weeks worked, which is necessary to calculate weekly earnings, and the industry and occupation of each person. The number of weeks worked are based on the 2000 calendar year, while the industry and occupation of respondents are based on the census reference week in May 2001.
Throughout the analysis, earnings is defined as annual employment earnings divided by the number of paid work weeks in the reference year. 5 Employment earnings include self-employment income, farm income and wages (labour market earnings). The sample was restricted further to those individuals with earnings greater than zero.
To accurately measure incomes earned in 2000, it was necessary to limit the sample further to persons who were in Canada in 2000 and had stayed in the same metropolitan area or rural classification within the same province. Otherwise, incomes earned during 2000 could have been attributed to the wrong geographic location.
To accurately measure earnings earned in 2000, it was necessary to limit the sample further to persons who were in Canada in 2000 and had stayed in the same metropolitan area or rural classification within the same province. Otherwise, incomes earned during 2000 could have been attributed to the wrong geographic location.
The subset of the population that satisfied the above conditions is 2,549,700 observations (unweighted) or about 42% of the detailed census file. Most of the descriptive analysis provided throughout this paper is based on this subset.
For much of the analysis, we make a broad distinction between urban and rural parts of Canada. In turn, these are further divided into sub-classes, providing us with a means to define an urban–rural spectrum. Urban areas are defined broadly as census metropolitan areas (CMAs) and census agglomerations (CAs) and, as such, encompass metropolitan areas that range in population from 10,000 to over 4 million. Recognizing this large population range, urban areas are subdivided into three size classes (see the classification of urban and rural areas below). Large Urban are CMAs with a population of 500,000 or more. Included in this category are Canada's largest metropolitan areas—Toronto, Montréal and Vancouver—but also somewhat smaller urban centres like Ottawa, Winnipeg and Québec. The Medium Urban class includes metropolitan areas that have a population from 100,000 to 499,999—e.g., Sherbrooke or Halifax. Finally, Small Urban areas have a population from 10,000 to 99,999—e.g., Moose Jaw or Stratford.
Classification of urban and rural areas
Urban areas
Large Urban: Census metropolitan areas (CMAs) with population above 500,000
Medium Urban: CMAs and census agglomerations (CAs) with a population from 100,000 to 499,999
Small Urban: CAs with population from 10,000 to 99,999
Rural areas associated with metropolitan influenced zones (MIZ)
Strong MIZ: 30% or more of the census subdivision's (CSD) labour force commutes to a CMA/CA
Moderate MIZ: 5% to 29% of the labour force commutes to a CMA/CA
Weak MIZ: Less than 5% of the CSD's labour force commutes to a CMA/CA
No MIZ: No commuting flows to a CMA or CA
Rural areas associated with urban areas: urban size class
Large Urban: Plurality of commuting flows is with a large urban area
Medium Urban: Plurality of commuting flows is with a medium urban area
Small Urban: Plurality of commuting flows is with a small urban area
Rural areas not associated with urban areas
Remote Rural: No commuting flows to a CMA or CA, or nearest CMA/CA is more than 200 kilometres away.
In the interest of creating a simplified urban–rural classification, most studies treat rural areas as a homogeneous group. In the Canadian context, however, this may be problematic; for example, rural parts of Newfoundland and Labrador are pooled with rural areas that fill the gaps between the cities of southern Ontario. In rural Newfoundland and Labrador, there is little opportunity for workers to commute to urban labour markets, while the opposite is true of rural southern Ontario. Proximity to urban labour markets provides rural workers with the option of obtaining higher paying urban-based jobs. This will tend to push up average earnings, either because these workers take urban-based jobs or because rural employers in these areas are in more competition for the local labour supply.
To provide a more nuanced view, rural areas are classified across two dimensions: their degree of labour-market integration via commuting flows with metropolitan areas and the size of the metropolitan area to which a plurality of their commuting flows go. Given this additional classification, it is expected that earnings will be higher in rural areas with stronger commuting flows to urban labour markets. Since earnings levels tend to increase (monotonically) with city size (Beckstead and Brown 2005), it is reasonable to expect rural areas with stronger links to larger urban labour markets to have higher earnings.
With respect to the first dimension, each rural area—census subdivision (CSD)—is assigned to a metropolitan influenced zone (MIZ) based on the strength of its commuting relationship with metropolitan labour markets. There are three MIZ classes: Strong MIZ includes rural areas where more than 30% of their employed population commute to a CMA/CA; Moderate MIZ includes CSDs whose commuter flows account for between 5% and 30% of their employed population and Weak MIZ includes CSDs for which less than 5%, but more than 0%, of their employed workforce commutes to urban labour markets. Rural CSDs with no commuter links to metropolitan areas are classified as 'No MIZ.'
The second dimension of the classification involves assigning each rural CSD to a metropolitan area that accounts for the plurality of the CSDs outbound commuting flows. This allows the classification of each rural CSD based on the size class of its assigned metropolitan area: Large, Medium or Small. CSDs classified as 'No MIZ' are not allocated to a metropolitan area. Neither are rural CSDs that are more than 200 kilometres away from the nearest metropolitan region. 6 We combine these CSDs with the No MIZ classified CSDs to create a class of CSDs termed 'Remote Rural'.
Classifying rural areas across two dimensions—the size of urban centre with which they are associated and the strength of links to urban labour markets—allows us to create a total of 10 classes of rural areas (see Table 1). This might be an unwieldy number except that we can view these categories as a gradient, with those rural areas with strong links to Large Urban areas (Large-Strong) expected to be the most advantaged and those rural areas with only weak commuting links to Small Urban areas (Small-Weak) to be the least advantaged, with the exception of Remote Rural areas.
In addition to the characteristics of individuals across geographic units that can be drawn from the 2001 Census, we are also interested in the characteristics of firms that are found within geographic units. Although workers and firms cannot be directly linked using census data, it is possible to characterise the industries in which workers are employed. As noted above, productivity and earnings are expected to be higher in industry-geographies that are populated by larger plants. We utilize Statistics Canada's Business Register to calculate the share of employment in large plants—establishment employment greater that 200—for each industry-geography, where the geographic units are CMAs and CAs for urban areas and census divisions for rural areas. 7 The Business Register is also used to measure the share of employment in foreign-controlled firms in each industry-geography, which allows us to control for their potential effect on earnings.
4 Earnings differences across the urban–rural spectrum
As a prelude to the presentation of the multivariate statistical analysis, we first develop a simple descriptive analysis of the association between earnings levels and a set of potential explanatory variables. The discussion proceeds in two parts. In the first part, we establish the degree and nature of the variation in earnings levels across the urban–rural spectrum as defined above. The second part attempts to identify a set of variables that might explain urban–rural earnings differences. These are variables that may influence earnings and may also vary systematically across the urban–rural spectrum.
4.1 Earnings levels across the urban–rural spectrum
As noted above, earnings are expected to be highest in large metropolitan areas and lowest in rural areas. Within rural areas, those that have strong labour market links to urban areas, and especially large urban areas, are expected to display higher earnings levels than those rural areas with weak labour market linkages.
These expectations generally hold true for urban and rural areas. The average worker in Canada have average weekly earnings of $836 (Table 2). Workers in Large Urban areas earn just over $900 per week. Workers in Medium and Small Urban areas earn $805 and $766, respectively. This difference in earnings is even more pronounced as we proceed to the rural areas. Across rural areas average weekly earnings ranged from $680 to $760 and were generally below the earnings levels of Small Urban areas.
Within rural areas, earnings patterns are far more complicated. Chart 1 shows the percentage deviation in mean weekly earnings for all urban and rural classes relative to the Canadian level. Rural areas with a strong commuting relationship with urban areas—Strong metropolitan influenced zone (MIZ)—tend to be the least disadvantaged, with those linked to Large and Medium Urban areas having the smallest negative deviations. Interestingly, those rural areas that fall into the Moderate MIZ category are the most disadvantaged, regardless of their associated urban size class. In the extreme, average earnings in Medium-Moderate rural areas are 19% below the Canadian average and 27% below that of Large Urban areas. On the other hand, rural areas that are weakly associated with urban areas through commuting flows, or fall into the Remote Rural category, perform relatively well compared with other rural areas. This may be due to differences in industrial structure, since these regions may be host to resource-based industries—e.g., pulp and paper, oil and gas—that pay particularly high wages (Baldwin and Brown 2001). These are also places where employers may have to pay a wage premium to retain workers because of their relative remoteness—isolation pay. Finally, many of the jobs available in these areas involve considerable risk of personal injury, and so employers may have to pay extra—danger pay—to compensate.
The picture of the urban–rural earnings gap that emerges is one of relatively large urban–rural earnings differences, with earnings increasing with the size of urban area, and between rural and urban areas. The earnings gap is qualitatively similar to those experienced in the United States (Glaeser and Maré 2001, Yankow 2006). The strength of ties to urban labour markets affects rural earnings levels, but the influence of these ties is spatially circumscribed. Only those rural areas that are tightly linked to Large and Medium Urban labour markets appear to benefit from these links. In other rural areas, the strength of commuting links to urban areas or the size of urban area appears to have little positive influence on earnings levels. We now turn to the question of what might underlie these earnings differences.
4.2 Correlates of income differences
The identification of correlates of earnings differences rests on measuring those characteristics of individuals that influence their ability to obtain a higher earnings. In the standard Mincer (1974) formulation, earnings depend on the accumulation of human capital, which is positively related to years of schooling and years of work experience. We begin with a brief overview of the relationship between years of schooling and experience, and of earnings levels. Afterwards, we examine several other variables whose influence on earnings may vary from place to place—e.g., immigrant status.
As one would expect, earnings generally increase with years of schooling (Chart 2). There are two distinctive points, however, where the gradient of the line increases: at 12 years of schooling; and, to a lesser extent, at 15 years of schooling. The mean weekly earnings for workers with 1 to 12 years of education is a fairly flat line. Across this range of years, for every year of education, weekly earnings increases by $5. From 12 to 15 years, weekly earnings rises by an average of $43 per year of schooling, while from 16 to 19 years of schooling weekly earnings rises by $73 per year. Workers with more than 19 years of schooling enjoy mean weekly earnings that are double that of workers with less than 12 years of education. We will return to the significance of this changing gradient for the econometric estimation of urban–rural earnings differences.
As with years of schooling, more years of experience are generally associated with increased weekly earnings (Chart 3). 8 Across age cohorts, earnings increase rapidly with years of experience until about 10 years. After that point, years of experience has a declining influence on earnings levels. Beyond 34 years of experience there is an apparent negative relationship between weekly earnings and experience. This is not necessarily an indication of the true relationship, however. It is important to keep in mind that this is merely a cross-section of individuals. Different cohorts may vary in ways other than experience (see Luong and Hébert 2009). For instance, years of education may be lower for workers with more than 34 years of experience.
Given the wealth of empirical evidence of the positive association between earnings levels and both schooling and experience, the fact that we find the same relationships in the census data is not particularly surprising. As the objective of this paper is to understand what underlies the urban–rural earnings gradient, how average levels of education and experience vary across the urban–rural spectrum is of more immediate interest.
Chart 4 plots the average number of years of schooling and experience for workers located in each of the urban–rural classifications. They follow a countervailing pattern: average number of years of schooling increases with position along the urban–rural spectrum, while average number of years of experience falls. At least in part, this pattern is mechanical. Workers in urban areas spend more of their potential earning years in classrooms and enter the job market at a later age, relative to rural workers. For instance, Large Urban workers average 14 years in school and 20 years of job experience, while workers in Remote Rural areas average 12 years of school and 23 years of job experience. The effect of this countervailing pattern is to at least dampen the effect of years of schooling on urban earnings relative to rural earnings.
An additional characteristic of Chart 4 is the relatively small variation in the number of years of schooling across the urban–rural spectrum. The difference between the urban–rural class with the highest average years of schooling (Large Urban) and the lowest (Remote Rural) is just 1.85 years. This might imply that variation in years of schooling is not a significant contributor to urban–rural earnings differences. However, it is important to keep in mind that the relationship between years of schooling and earnings is non-linear, with earnings accelerating with 12 or more years of education (Chart 2).
The impact of additional years of schooling can be seen most clearly if we plot the incidence of degree holders across the urban–rural spectrum (Chart 5). In contrast to average years of schooling, the extent of variation in degree-holder incidence is large—the incidence in Large Urban areas is roughly twice that of the rural classes. These two additional years of schooling in Large Urban areas translated into a significant difference in the share of degree holders. As degree holders, on average, earn 40% more than non-degree holders (2001 Census of Population) their presence may have a significant impact on average earnings levels. The lesson to be drawn here is that fairly small differences in average years of schooling across urban and rural classes may translate into significant earnings differences. Any econometric model that seeks to account for urban–rural earnings variation will have to be sensitive to the non-linear relationship between earnings and education; otherwise, the estimated impact of education on earnings levels may be underestimated.
There are numerous other individual characteristics that likely affect earnings levels. Table 3 presents the means (and standard deviations) for these variables. The table begins with gender and full/part-time status. Women tend to earn less than men; and part-time workers less than full-time wokers, which may be due to fewer hours worked per week and/or lower earnings per hour. The effect of gender and full/part-time status on urban–rural earnings differences is likely to be weak because we expect there to be relatively little variation in their composition across urban and rural areas.
In contrast to gender and full-time/part-time status, Aboriginal/visible-minority status and immigrant status may vary significantly across urban and rural areas. We expect Aboriginal people to make up a relatively large portion of the population of more remote rural regions, while non-Aboriginal visible minorities and immigrants are likely to be much more prevalent in larger urban centres. Both visible minorities and Aboriginal people earn less than the non-Aboriginal/visible-minority part of the Canadian population. Contrary to commonly held perceptions, immigrants earn about the same level of earnings as Canadian-born workers (Table 3). However, if we classify immigrants based on the number of years since immigration, a different picture emerges. Mean weekly earnings for new immigrants are significantly lower than those of the Canadian-born population.
However, this effect changes as the immigrant cohort that has been living in Canada for more than 15 years earns as much as, if not more than, Canadian-born workers. 9 To the extent that visible minorities and new immigrants are concentrated in Canada's largest cities, they may pull down average earnings there, while Aboriginal people will tend to dampen earnings in more remote rural areas.
Finally, the source of earnings of individuals may also influence earnings levels. The 2001 Census identifies three sources of earnings: wages, self-employed income (non-farm) and farm self-employed income. As is evident in Table 3, self-employed farmers earn significantly less than wage earners and other self-employed individuals, whose earnings are roughly equal. Since workers who earn their income from farming are naturally more prevalent in rural areas, they may draw rural earnings levels down.
5 Multivariate analysis
Drawing on theory and empirical evidence, we have posited that human capital composition and agglomeration economies underlie urban–rural earnings gaps. The goal of this section is to establish the relative contribution of these effects.
There are two approaches to establish the effect of agglomeration economies on earnings levels. The first approach is to treat the position of a city or rural area along the urban–rural spectrum as an indirect measure of agglomeration economies. By melding a set of binary variables that capture the urban–rural spectrum with measures of human capital, the impact of the latter on urban–rural earnings differences can be assessed. This approach has the benefit of allowing us to directly address the question of how human capital composition influences the urban–rural earnings differences that were so evident in Chart 1. This approach is hampered by the cumbersome set of binary variables required to fully take into account the urban–rural spectrum.
The second approach is to measure agglomeration economies directly. This can be accomplished by associating with each individual worker the level of his or her industry's employment and total employment within their geographic unit. The former is a proxy for localization economies, while the latter is a proxy for urbanization economies. This provides the benefit of testing for the effect of agglomeration economies within a fairly simple and, consequently, more easily interpretable framework. Since both approaches have merit, we apply both to the multivariate analysis, beginning with the second.
5.1 Earnings model
We estimate a simple econometric model that in its most generalized form
is specified as follows:

where i indexes employed persons, j locations (census metropolitan
areas, census agglomerations, or rural census divisions) and k industries.
Weekly earnings are represented by wi. The vectors A and H are measures of agglomeration economies and human capital,
respectively. The vector I encompasses a broad set of personal characteristics
that might also influence earnings levels outlined in Table 3—e.g., immigrant status. Also included in the fully specified
model is a set of provincial (pi) and industry–occupation
(ioi) fixed effects. Provincial fixed effects are
included to account for the effects of provincial policy on earnings levels
and variation in non-human capital endowments that might be captured by provincial
boundaries—e.g., Alberta's oil reserves. The industry–occupation
fixed effects are included to capture the effects of a person's industry
and occupation on earnings levels that might not be captured by measures of
education and experience. Persons are classified by industry and occupation
to capture their joint effect: for instance, a lawyer who works in the financial
sector likely earns a higher wage than a lawyer who works in the public sector.
Finally, the model includes a set of controls for industrial organization;
that is, the share of employment in industry k in location j in
large plants 10 (sijk) and foreign-controlled
plants (fijk).
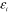 is a standard stochastic error term.
is a standard stochastic error term.
To estimate the effects of human capital on earnings levels we incorporate,
at least initially, the standard Mincer equation, represented here by the
vector H:
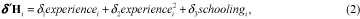
where experience and schooling are defined
as above.
5.2 Econometric issues
The primary econometric issue associated with estimating Equation (1) is the correlation of the error term with employment levels. This correlation may stem from unobserved abilities and skills, and/or the endogeneity of earnings and employment levels. We address these problems using several strategies.
Omitted variable bias may stem from the sorting of persons with unobserved skills and abilities into larger cities, biasing upward the estimated effect of city size on earnings levels. This potential source of bias is addressed in two ways. The first is to add a large number of controls—e.g., for industry and occupation—to the model, which is the standard solution when working with cross-sectional data. While not without merit, this solution is ultimately unsatisfactory because unmeasured skills and abilities may remain, even after adding extensive controls. 11
The second approach is to use an estimator that is less sensitive to this particular form of omitted variable bias. Here we rely on the nature of the problem to develop a potential solution. The problem is that workers with better skills and abilities may sort into larger urban areas because returns to these—observed or unobserved—attributes may increase with city size. However, workers are more likely to migrate when the net present value of the stream of expected gains in earnings from migration exceeds its monetary and social costs. Given that the costs of migration are largely invariant across earnings levels, 12 the incentives to migrate (sort) will be stronger for individuals who expect to earn relatively high earnings, particularly for those workers whose unobserved abilities might translate into significant earnings gains (the 'stars').
If the incentive to migrate into larger centres is stronger for workers with higher potential earnings, then it becomes important to minimize the effect of these higher earning migrants on our estimates. We do so by re-estimating our models using a quantile estimator that allows the conditional response of earnings to employment levels to vary across various points in the earnings distribution. 13 Our expectation is that the effect of city size will be stronger for the higher quantiles of the earnings distribution in response to these unobserved characteristics of workers. This approach serves to reduce the effect of unobserved skills and abilities on our estimates, but some effect may still remain if better skills and abilities are associated generally with the decision to migrate.
The second econometric issue is the endogeneity of earnings and city size. As noted by Combes et al. (2007), a local shock or characteristics of a location that are unaccounted for may be driving both population size and earnings levels. The general response to this problem is to find an instrument that is correlated with city size, but not with earnings. The most commonly used instrument is city size lagged many decades into the past. This 'deep' lagging serves to break the contemporaneous correlation of the error term with city size that might stem from local shocks. However, the lag of city size may still be invalid if some past characteristic drives both previous population levels and current earnings levels. If true, the lag of city size would still be correlated with the error term. For instance, lagging Calgary's population only 30 years would be insufficient because the oil industry was an important driver of Calgary's population at that time and for earnings levels today. Hence, the use of lagged population levels also relies on the argument that the sources of productivity have sufficiently changed over the lagged period such that previous sources of comparative advantage are no longer relevant. This argument also underpins the less common use of geological characteristics as instruments: such characteristics as soil quality might have been important drivers of population in the past but are now far less important to modern production (Combes et al. 2007).
Combes et al. (2007) use both types of instruments and obtain qualitatively similar results for both. Moreover, they find that, after instrumenting, there is little change in the estimated effects of agglomeration economies on earnings levels, regardless of the type of instrument used—i.e., the lag of population density or geological characteristics. Although it would appear that the biasing effect of endogeneity is quite small, we nevertheless develop an instrument for the level of employment in each geographic unit.
Ideally, it would be best to use the long lag of city populations as an instrument. However, it is difficult to develop consistent estimates of the populations of contemporary cities and rural areas in Canada using historical data. As an alternative, we take advantage of the fact that cities rarely experience significant shifts in their ranks over time. Hence, it is possible to use the 'coarse' employment rank of cities and rural areas as an instrument. To develop this ranking, the employed workforces of all 399 geographic units were ranked and then divided into 10 groups, of about 40 units each, that are in turn, ranked from 1 to 10. It is unlikely such a ranking will be susceptible to contemporaneous shocks. Moreover, each city's coarse ranking is likely to be highly correlated with its position decades into the past. For instance, in 1941 Calgary had a population of 87,267 (1941 Dominion Census). This is greater than Kamloops in 2001, the smallest urban area in the top-ranked group. 14 Calgary would have remained in the top group even if it had not added population over the period. We are less sanguine about smaller cities and rural areas because the employment ranges within each group are smaller and therefore it is more likely that cities ranked more highly today were not so in previous decades.
As a final econometric note, we are regressing aggregate variables on micro-variables, which, as Moulton (1990) has illustrated, can result in significant underestimation of the standard errors of regression coefficients. We adjust all standard errors for this effect, as well as for heteroskedasticity.
Before reporting the regression results, we note that for the regression models presented we use a one-in-five sample of the main dataset, unless indicated otherwise. We used this approach to reduce computational burden. Tests run on the simpler (less burdensome) models with the full dataset demonstrated that moving to a smaller sample had no qualitative impact on the estimates.
5.3 Econometric results
We begin the analysis by estimating a set of models that only include variables designed to account for agglomeration economies (Table 4). The first model includes employment in locationj alone. As expected, there is a positive and significant association between employment levels and earnings, with an elasticity of 0.05, which implies a doubling of employment would result in about a 5% increase in earnings. Regressing average earnings on employment levels across geographic units in France, Combes, Duranton and Gobillon (2008) obtain a similar elasticity of about 0.05. Model 2 incorporates the employment level of the industry in which person i works. Its coefficient is only weakly significant, while the coefficient on employment levels is reduced, but remains significant. Models 3 and 4 substitute employment density for employment levels. They provide qualitatively similar results to the corresponding models using employment levels. Throughout the analysis we will utilize employment levels at the region and industry levels as a means to estimate the effect of agglomeration economies, since they most closely match our size-based characterization of the urban–rural spectrum.
Table 5 presents parameter estimates of model Equation (1), beginning with only the agglomeration and human capital vectors and then adding sets of controls until the fully specified model is estimated. Model 1 includes only the agglomeration and human capital variables. Consistent with other estimates of the Mincer equation, experience and years of schooling have a positive effect on earnings levels, with the effect of each additional year of experience declining as the level of experience increases. While the effect of experience on earnings declines with the level of experience, the estimated coefficients imply it never reaches the point during a working lifetime when its influence becomes negative. The effect of accounting for human capital is to reduce the coefficient on employment from 0.035 (Model 2, Table 4) to 0.023, or by about one third. The coefficient on industry employment is qualitatively the same.
In the descriptive analysis we noted that there is a non-linear relationship between years of schooling and average earnings. If this is not properly accounted for in the econometric specification, the effect of agglomeration economies may be overestimated if individuals with above average years of schooling are concentrated in larger urban areas. To account for this possibility, we re-estimate Model 1 using a spline, with knots at 12 and 16 years of schooling, corresponding to the changes in the slope of the schooling-earnings curve presented in Chart 3. This allows for separate coefficients on years of schooling for less than 12 years, 12 to 16 years and greater than 16 years. Model 2 replicated Model 1, while allowing different coefficients on years of schooling to vary by the three schooling ranges.
The effect of years of schooling varies considerably, depending on the range of years. For less than 12 years of schooling, each additional year of schooling increases earnings by about 3%. This contrasts with 11% and 7% for 12 to 16 years and greater than 16 years, respectively. The most powerful impact of schooling on earnings derives from those years of schooling from 12 years and above.
The use of the spline also affects the coefficient of employment. The coefficient on employment falls from 0.023 to 0.020. Hence, by taking into account standard measures of human capital with a specification that is sensitive to the varying effects of years of education on earnings levels, the effect of employment size on earnings levels is substantially reduced—from 0.035 to 0.020.
There are, of course, other characteristics of individuals that influence earnings levels that may not be randomly distributed across urban and rural areas. Immigrants and visible minorities tend to be concentrated in larger cities. To the extent that members of these groups are paid less than average, not accounting for them may result in the underestimation of the effect of employment size on earnings levels. Similarly, the concentration of Aboriginal populations and persons who derive their earnings from farming in rural areas may result in the overestimation of the effect of employment size on earnings. Model 3 takes these factors into account, while also including controls for the effects of gender, full- and part-time job status, industry–occupation and province of residence.
The effect of the inclusion of these controls on the agglomeration variables is modest. The coefficient on employment falls, as does the coefficient on industry employment. The most noteworthy change is that the coefficient on industry employment is now statistically significant, suggesting localization economies may positively influence earnings levels.
While the coefficients on the agglomeration variables are only slightly perturbed by the inclusion of these controls, this is not the case for the human capital variables. The coefficients on experience and years of schooling are reduced substantially. This stems largely from the inclusion of industry–occupation fixed effects. Older workers who, by definition, have more experience may be concentrated in higher paying industries or have been promoted into higher paying occupations (e.g., managers). Similarly, workers with more years of education are likely to be working in occupations (e.g., medical doctors) and industries (e.g., finance), which pay more.
Turning briefly to the added controls, gender and full-time status have a positive influence on earnings. All else being held equal, men earn about 18% more than women and full-time workers earn about 54% more than part-time workers. The difference between full- and part-time worker earnings likely derives from fewer hours worked per week by part-time workers. One concern is that the lower number of hours worked per week by part-time workers may weaken the link between earnings and actual levels of productivity. To address this problem, we re-estimated the models with part-time workers excluded and obtained qualitatively similar results (Appendix Table 1).
Self-reporting Aboriginal people and visible minorities earn about 10% less than those who do not fall into these groups. On balance, immigrants tend to earn less than the Canadian born, but the earnings differences between these two groups decrease as the number of years since immigrating to Canada increases. Persons who obtain their income through wages earned about 23% more per week than those who earned their income through farming, and about 30% more than the self-employed.
The last model addresses the effect of industrial organization on earnings differences by adding measures of the size of establishments and foreign control. As expected, both variables have a positive and significant effect on earnings levels. Doubling the share of employment, in either larger establishments or foreign-owned establishments, increased earnings by about 5%. With the inclusion of these controls, the coefficient on employment size increased only marginally. However, the coefficient on industry employment, while remaining significant, was reduced by about 40%. Wheeler (2006) obtains a similar result. Hence, there appears to be an industrial organization effect, but its interpretation is open to question. While this result suggests a lesser role for localization economies, it might also be that these economies underlie the larger size of establishments found in employment clusters.
While the models presented in Table 5 provide an extensive set of controls, they are by no means comprehensive. For instance, our measures of agglomeration economies are limited as we are not including market potential, a broader measure of market size. The models also do not include controls for local amenities. This may be important, because workers may accept lower earnings to live in locations with better amenities. Finally, as noted above, employment may be endogenous, which implies we need to instrument for employment.
Table 6 presents models that test for the robustness of our results by controlling for these various effects. For ease of comparison, Model 1 is the same as Model 2 presented in Table 5, with the coefficient estimates for the human capital variables left unreported. We prefer this model because it is the most parsimonious. Models 2 and 3 merely add additional variables to this model, while Model 4 presents the instrumental variable estimates.
Model 2 includes a control for market potential as specified
originally by Harris (1954). Market potential is measured using the sum of
the populations of Canadian census metropolitan areas and rural census divisions
and U.S. counties weighted (negatively) by distance.More formally, market
potential (MP) is given by
 , where j and l index geographic
units (census metropolitan areas, census agglomerations, census divisions
and, in the U.S., counties), P is the population of each unit and D is the great circle distance between j and l. 15 U.S. counties are included because of the particularly strong effect
of the U.S. market on parts of Canada, particularly southern Ontario and Quebec. 16 As expected, there is a positive association between market
potential and earnings, but the coefficient is insignificant. 17 Market
access beyond that of the local urban or rural area has no significant effect
on earnings.
, where j and l index geographic
units (census metropolitan areas, census agglomerations, census divisions
and, in the U.S., counties), P is the population of each unit and D is the great circle distance between j and l. 15 U.S. counties are included because of the particularly strong effect
of the U.S. market on parts of Canada, particularly southern Ontario and Quebec. 16 As expected, there is a positive association between market
potential and earnings, but the coefficient is insignificant. 17 Market
access beyond that of the local urban or rural area has no significant effect
on earnings.
The subsequent model (Model 3) attempts to control for amenities. The share of employment in culture occupations 18 in each geographic unit is used as a proxy for amenities. As noted by Glaeser and Gottlieb (2006, pp. 1276–1277), "…migration across cities ensures that cities that are more attractive along one dimension (such as having higher wages), are less attractive along some other dimension (such as having worse weather)". 19 Hence, earnings are expected to be negatively associated with culture employment (a positive amenity). Since culture employment generally increases with city size in Canada (Schimpf and Sereda 2007), the coefficient on city size is expected to increase with the inclusion of culture share of employment in the model. Both expectations are borne out in the estimates. The coefficient on the culture share of employment is negative and significant at the 10% level, while the elasticity on city size increases from 0.018 (Model 1) to 0.026.
The last model in Table 6 seeks to control for the potential endogeneity of earnings and employment size by instrumenting for employment using the rank of employment. As this instrument is fairly strong, with a partial R-squared equalling 0.35, we used two-stage least squares (2SLS) to estimate the model. The 2SLS estimate of the coefficient for employment is similar to that of the base model and remained significant. This is not entirely unexpected, as Combes et al. (2007) find the effect of the endogeneity of employment density—which is closely associated with our measure of agglomeration economies—and earnings, to be small.
Finally, we turn to the issue of omitted variable bias. As noted above, our estimate of the effect of agglomeration economies on earnings that stems from the level of employment in region j may be biased upward due to omitted variables. That is, we are concerned with the possibility that individuals with unobserved characteristics that are positively associated with earnings will be concentrated in larger urban areas. To address this problem, we estimate a set of quantile regressions using the specification that matches that of Model 2 in Table 5. The quantile point estimates and 95% confidence intervals (Q lower and Q upper bound) for employment inj are presented in Chart 6. For ease of reference, the ordinary least squares (OLS) point estimate is also presented.
For much of the earnings distribution, the quantile point estimate for employment in j is below the OLS estimate, with the average estimate between the 10th and 90th percentiles of 0.016. It is only at the 95th percentile that the quantile estimate exceeds the OLS estimate (coefficient=0.024). This suggests that the right tail of the earnings distribution draws the OLS point estimate for employment in j upwards. The right tail of the earnings distribution also likely includes individuals whose unobserved characteristics lead to higher earnings. Hence, we place more emphasis on the 0.016 point estimate; although we note that this point estimate is not so different from the OLS estimate of 0.020.
As a final note, the 5th percentile point estimate is about half that of the other quantile estimates. This might be interpreted as an indication that agglomeration economies are less important for very low-earnings workers. But it is important to keep in mind the precision of this estimate is quite low. The upper bound of its 95% confidence interval roughly matches that of the other quantiles, with the exception of the 95th percentile.
We conclude the analysis by returning to the original problem of developing an understanding of the urban–rural earnings gap. The multivariate analysis suggests earnings differences across the urban–rural spectrum are associated with both agglomeration economies related to city size and differences in the human capital composition of geographic units. The question at hand is how much of the variation in earnings across the urban–rural spectrum is accounted for by differences in the skill composition of their workforces. To address this question, we estimated two models. The first includes only binary variables for each of the urban–rural classes, with Large Urban excluded. The second model corresponds to Model 2 in Table 4, with the agglomeration variables excluded. We are interested in the reduction in the values of the coefficients of the urban–rural binary variables with inclusion of measures of human capital. It is evident from Chart 7 that for Medium and Small Urban areas, about 40% of their earnings gap with Large Urban areas is accounted for by differences in the human capital composition of their employed workforces. For rural areas, between one-third and one-half of their gap is accounted for by the level of human capital obtained by their workers. These estimates are remarkably close to those of Combes, Duranton and Gobillon (2008), who find from 40% to 50% of the variation in earnings across labour market areas in France are accounted for by observed and unobserved differences in skills and abilities. Particularly instructive is that their estimate is based on a methodology that explicitly takes into account unobserved characteristics. We obtain a similar result by utilizing a specification that is sensitive to the effects of higher education on earnings levels. It is education that is one of the key underlying correlates of the variation in urban–rural earnings in Canada. The remainder is likely due to agglomeration economies that are proxied by our definition of urban and rural areas. However, because of the sensitively of the OLS estimator to unobserved characteristics of individuals, we also have to acknowledge that these may also account for a portion of these differences, in addition to other idiosyncratic factors.
6 Conclusion
Employment earnings vary considerably across Canadian cities and rural areas. The earnings of persons in large metropolitan areas are about 25% higher than their rural counterparts. A natural question is what underlies this gap. In this paper, we asked whether such differences are due to agglomeration economies, which are arguably stronger in larger urban areas, or because workers with higher levels of human capital tend to concentrate in cities.
The analysis demonstrates that both agglomeration economies captured by city size and skill composition are associated with earnings differences between cities and rural areas. Skill differences are clearly associated with earnings levels: the number of years of schooling appears to account for a large part of the gap in urban–rural earnings. The advantage of cities appears to lie as much in their capacity to educate, attract and retain highly skilled workers, as in their innate ability to facilitate the interaction of workers and firms.
Two questions follow from this analysis. The first is what underlies agglomeration economies? (See Beckstead et al. 2007 and Baldwin, Brown and Rigby 2008.) The second is why are more highly skilled workers concentrating in larger cities? More to the point, is the supply of worker skills and the demand for these same skills endogenous to cities? Are industries and firms that require workers with specialized skills more likely to develop in areas where there is a larger pool of specialized labour (Kim 1989), creating a demand for specialized skills? Similarly, do workers invest in more years of schooling in places where the returns to that investment are the highest and the most evident; or do skilled workers emerge everywhere at the same rate, and then migrate to where the returns to their education are highest?
7 References
Aydemir, Abdurrahman, and Mikal Skuterud. 2004. Explaining the deteriorating entry earnings ofCanada's immigrant cohorts: 1966–2000. Analytical Studies Branch Research Paper Series. Catalogue no. 11F0019MIE2004225. Ottawa: Statistics Canada.
Adamson, Dwight W., David E. Clark and Mark D. Partridge. 2004. "Do urban agglomeration effects and household amenities have a skill bias?"Journal of Regional Science. 44, 2: 201–223.
Andersson, Fredrik, Simon Burgess and Julia I. Lane. 2007. "Cities, matching and the productivity gains of agglomeration." Journal of Urban Economics. 61, 1: 112–128.
Baldwin, John R, Desmond Beckstead, W. Mark Brown and David L. Rigby. 2007. "Agglomeration and the geography of localization economies in Canada." Regional Studies. 42, 1: 117–132.
Baldwin, John R., W. Mark Brown and Tara Vinodrai. 2001. Dynamics of the Canadian Manufacturing Sector in Metropolitan and Rural Regions. Analytical Studies Branch Research Paper Series. Catalogue no. 11F0019MIE2001169. Ottawa: Statistics Canada.
Baldwin, John R., W. Mark Brown and David L. Rigby. 2008. Agglomeration Economies: Microdata Panel Estimates from Canadian Manufacturing. Economic Analysis (EA) Research Paper Series. Catalogue no. 11F0027MIE2008049. Ottawa: Statistics Canada.
Beckstead, Desmond, and W. Mark Brown. 2005. Provincial Income Disparities Through an Urban-rural Lens: Evidence from the 2001 Census. Insights on the Canadian Economy Research Paper Series. Catalogue no. 11-624-MIE2005012. Ottawa: Statistics Canada.
Beckstead, Desmond, W. Mark Brown and Guy Gellatly. 2008. Citiesand Growth: The Left Brain of North American Cities: Scientists and Engineers and Urban Growth. The Canadian Economy in Transition Series. Catalogue no. 11-622-MIE2008017. Ottawa: Statistics Canada.
Combes, Pierre-Philippe, Gilles Duranton and Laurent Gobillon. 2008. "Spatial wage disparities: Sorting matters!"Journal of Urban Economics. 63, 2: 723–742.
Combes, Pierre-Philippe, Gilles Duranton, Laurent Gobillon and Sébastien Roux. 2007. Estimating agglomeration effects: Does playing with different instruments give a consistent tune? Draft working paper.
Costa, Dora L., and Matthew E. Khan. 2000. "Power couples: Changes in the locational choice of the college educated, 1940–1990."The Quarterly Journal of Economics. 115, 4: 1287–1315.
Davies, Stephen W., and Bruce R. Lyons. 1991. "Characterising relative performance: the productivity advantage of foreign owned firms in the UK." OxfordEconomic Papers. 43, 4: 584–595.
Florida, Richard. 2003. The Rise of the Creative Class: And How It's Transforming Work, Leisure, Community and Everyday Life. New York: Basic Books.
Florida, Richard, 2002. "The economic geography of talent." Annals of the Association of American Geographers. 92, 4: 743–755.
Fu, Shihe, and Stephen L. Ross. 2007. "Wage premia in employment clusters: Agglomeration economies or worker heterogeneity?" University of Connecticut Department of Economics Working Paper Series. Working Papers 2007-26. Storrs, CT: University of Connecticut.
Glaeser, Edward L., and Joshua D. Gottlieb. 2006. "Urban resurgence and the consumer city." Urban Studies. 43, 8: 1275–1299.
Glaeser, Edward L., and David C. Maré. 2001. "Cities and skills." Journal of Labor Economics. 19, 2: 316–342
Harris, Chauncy D. 1954. "The market as a factor in the localization of industry in the United States." Annals of the Association of American Geographers. 44, 4: 315–348.
Helsley, Robert W., and William C. Strange. 1990. "Matching and agglomeration economies in a system of cities." Regional Science and Urban Economics. 20, 2: 189–212.
Henderson, J. Vernon. 2003. "Marshall's scale economies." Journal of Urban Economics. 53, 1: 1–28.
Holmes, Thomas J., and John J. Stevens. 2002. "Geographic concentration and establishment scale." Review of Economics & Statistics. 84, 4: 682–690.
Idson, Todd L., and Walter Y. Oi. 1999. "Workers are more productive in large firms." The American Economic Review. 89, 2: 104–108.
Jacobs, Jane. 1969. The Economy of Cities. New York: Random House.
Kim, Sunwoong. 1989. "Labor specialization and the extent of the market." Journal of Political Economy. 97, 3: 692–705.
Luong, May, and Benoit-Paul Hébert. 2009. "Age and Earnings." Perspectives on Labour and Income 10, 1: 5–11. Catalogue no. 75-001-XPE. Ottawa: Statistics Canada.
Marshall, Alfred. 1890. Principals of Economics. London: Macmillan and Company.
Mincer, Jacob. 1974. Schooling, Experience and Earnings. New York: Columbia University Press.
Moulton, Brent R. 1990. "An illustration of a pitfall in estimating the effects of aggregate variables on micro units." Review of Economics & Statistics. 72, 2: 334–338.
Rauch, James E. 1993. "Productivity gains from geographic concentration of human capital: Evidence from the cities." Journal of Urban Economics. 34, 3: 380–400.
Rosenthal, Stuart S., and William C. Strange. 2008. "The attenuation of human capital spillovers." Journal of Urban Economics. 64, 2: 373–389.
Schimpf, Michael, and Paul Sereda. 2007. Towards a Geography of Culture: Culture Occupations Across the Canadian Urban-Rural Divide. Culture, Tourism and the Centre for Education Statistics Research Papers. Catalogue no. 81-595-MIE2007053. Ottawa: Statistics Canada.
Wheeler, Christopher H. 2006. "Productivity and the geographic concentration of industry: The role of plant scale." Regional Science and Urban Economics. 36, 3: 313–330.
Yankow, Jeffrey J. 2006. "Why do cities pay more? An empirical examination of some competing theories of the urban wage premium." Journal of Urban Economics. 60, 2: 139–161.
- Date modified:
