Map projection
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
Detailed definition
A map projection is the process of transforming and representing positions from the earth's three-dimensional curved surface to a two-dimensional (flat) surface. The process is accomplished by a direct geometric projection or by a mathematically derived transformation.
The Lambert conformal conic map projection is widely used for general maps of Canada at small scales and is the most common map projection used at Statistics Canada.

Censuses
2011, 2006, 2001, 1996, 1991, 1986, 1981, 1976 (Lambert conformal conic)
1996, 1991, 1986, 1981, 1976, 1971 (Transverse Mercator)
Remarks
The Earth's surface cannot be flattened without distorting geometrical properties, such as area, shape, distance and direction. These spatial properties can be preserved individually (at least locally) and in certain combinations on map projections. However, the four basic properties of area, shape, distance and direction cannot all be held true simultaneously. Therefore, it is important to select a projection having the properties that are suited to the mapping situation. For example, a projection that accurately represents the shapes of the continents will distort their relative sizes.
The Lambert conformal conic projection (Figure 14) provides good directional and shape relationships for mid-latitude regions having a mainly east-to-west extent. Standard parallels at 49° N and 77° N are most commonly used. The scale is correct along the standard parallels only; areal deformation decreases between and increases away from the standard parallels. The central meridian, normally at 91° 52' W, is a straight line about which the projection is symmetrical. False eastings and northings are given to ensure positive coordinate values in linear units of measure (metres).
Figure 14
Example of a map projection and unprojected coordinates
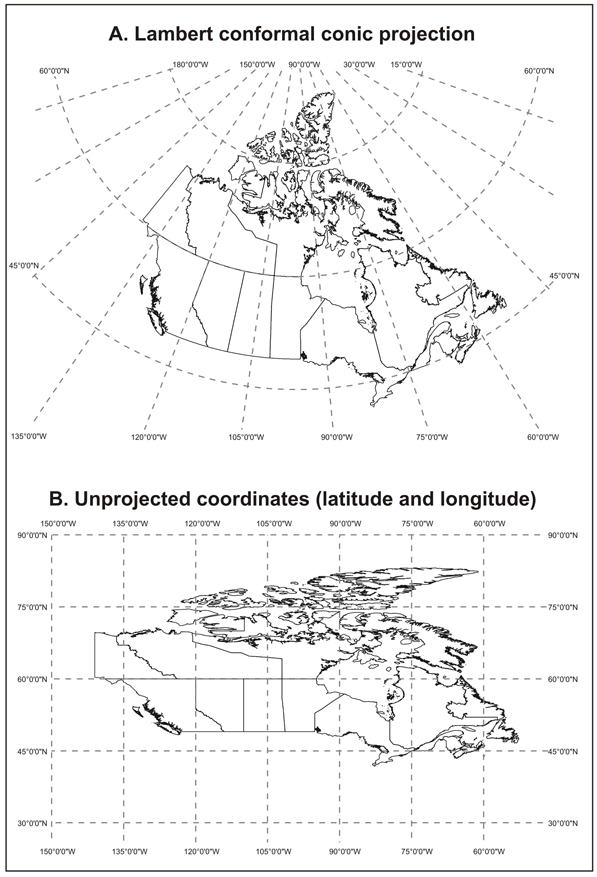
Source: Statistics Canada, 2011 Census of Population.
Latitude and longitude is not a map projection, as the coordinates are spherical (angular units of measure such as degrees, minutes and seconds) therefore unprojected. It is recommended that maps not be generated using these spherical coordinates because they result in maps that are distorted (Figure 14).
The Lambert conformal conic map projection is the working projection for cartographic boundary files, digital boundary files, road network files and the Spatial Data Infrastructure, and for generating representative points.
Refer to related definitions of cartographic boundary files (CBFs); coordinate system; datum; digital boundary files (DBFs); representative point; road network file (RNF) and Spatial Data Infrastructure (SDI).
Changes prior to the current census
Prior to 2001, street network files were based on the Transverse Mercator map projection/Universal Transverse Mercator (UTM) coordinate system.
- Date modified:
