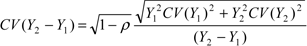Section 7: Data quality
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
Non-sampling errors
Errors, which are not related to sampling, may occur at almost every phase of a survey operation. Interviewers may misunderstand instructions, respondents may make errors in answering questions, the answers may be incorrectly entered and errors may be introduced in the processing and tabulation of the data. These are all examples of non-sampling errors.
Over a large number of observations, randomly occurring errors will have little effect on estimates derived from the survey. However, errors occurring systematically will contribute to biases in the survey estimates. Quality assurance measures are implemented at each step of the data collection and processing cycle to monitor the quality of the data. These measures include the use of highly skilled interviewers, extensive training of interviewers with respect to the survey procedures and questionnaire, observation of interviewers to detect problems of questionnaire design or misunderstanding of instructions, edits to ensure that data entry errors are minimized and coding and edit quality checks to verify the processing logic.
Sampling errors
The Labour Force Survey collects information from a sample of households. Somewhat different figures might have been obtained if a complete census had been taken using the same questionnaires, interviewers, supervisors, processing methods, etc. as those actually used in the Labour Force Survey. The difference between the estimates obtained from the sample and those that would give a complete count taken under similar conditions is called the sampling error of the estimate, or sampling variability. Approximate measures of sampling error accompany Labour Force Survey products and users are urged to make use of them while analysing the data.
Three interpretation methods can be used to evaluate the precision of the estimates: the standard error, and two other methods also based on standard error: confidence intervals and coefficients of variation.
Interpretation using standard error
The sampling error, or standard error, is a measure that quantifies how different the sample estimate might be from the census value. It is based on the idea of selecting several samples, although in a survey only one sample is drawn and information is collected on units in that sample. Using the same sampling plan, if a large number of samples were to be drawn from the same population, then about 68% of the samples would produce a sample estimate that is within one standard error of the census value and in about 95% of the samples it will be within two standard errors of the census value.
When looking at changes, for example month to month changes, two thirds of the time (68%) a change greater than the sampling error indicates a real change. The larger the change compared to the standard error, the better the chance that we are observing a real change, as opposed to a change due to sampling variability. At the 95% confidence level, the change in the estimate must be greater than twice the sampling error in order to ensure that change is real.
Movements in estimates that are smaller than the sampling error are less likely to reflect a real change and more likely to be due to sampling variability. While the above is true for monthly movements, one can have more confidence in a series of consecutive movements in the same direction, even though some of the monthly movements may be smaller than the sampling error.
To illustrate, let us say that between two months the published estimate for total employment increases by 40,000, and that the associated standard error for the movement estimate is 27,200. Since the increase is larger than the standard error, the probability is at least two out of three (68%) that the increase of 40,000 in employment is a real change. To reach a 95% confidence level, the standard error has to be doubled. Because the increase of 40,000 in employment is smaller than twice the standard error (54,400), it is impossible to state with a 95% confidence level that there was an increase in employment.
Interpretation using confidence intervals
Confidence intervals provide another way of looking at the variability inherent in estimates of sample surveys. To illustrate how to calculate the confidence interval, let us say that one month the published estimate for total employment rose by 16,000 to reach 16,500,000. The associated standard error for the movement estimate is 27,200. Using the standard error to build the confidence intervals, we can say that:
- There are approximately two chances in three (68%) that the real value of the movement between the two months falls within the range -11,200 to +43,200 (16,000 + or – one standard error).
- There are approximately nine chances in ten (90%) that the real value of the movement between the two months falls within the range -27,520 to +59,520 (16,000 + or – 1.6 times the standard error).
- There are approximately nineteen chances in twenty (95%) that the real value of the movement between the two months falls within the range -38,400 to +70,400 (16,000 + or – two standard errors).
Interpretation using coefficient of variation
Sampling variability can also be expressed relative to the estimate itself. The standard error as a percentage of the estimate is called the coefficient of variation (CV) or the relative standard error. The CV is used to give an indication of the uncertainty associated with the estimates. For example, if the CV is 7%, then in 68% of the samples the census value will lie within plus or minus 7% or one CV and in 95% of the samples the census value will lay within plus or minus 14% or two times the CV of the estimate.
Small CV's are desirable because they indicate that the sampling variability is small relative to the estimate. The CV depends on the size of the estimates, the sample size the estimate is based on, the distribution of the sample, and the use of auxiliary information in the estimation procedure. The size of the estimates is important because the CV is the sampling error expressed as a percentage of the estimate. The smaller the estimate the larger the CV (all other things being equal). For example, when the unemployment rate is high the CV may be small. If the unemployment rate falls due to improved economic conditions then the corresponding CV will become larger. Typically, of similar estimates, the one with largest sample size will yield the smaller CV. This is because the sampling error is smaller.
Also, estimates referring to characteristics that are more clustered will have a higher CV. For example, persons employed in forestry, fishing, mining, oil and gas in Canada are more clustered geographically than employed women aged 55 to 64 years in Ontario. The latter will have a smaller sampling variability although the estimates are of approximately the same size.
Finally estimates referring to age and sex are usually more reliable than other similar estimates because the LFS sample is calibrated to post-censal population projections of various age and sex groupings. Continuing the previous example, persons employed part-time in Alberta will have a larger sampling variability than employed men aged 35 to 44 years in British Columbia although the estimates are of similar size.
Variability of monthly estimates
To look up an approximate measure of the CV of an estimate of a monthly total, please consult table 7.1, which gives the size of the estimate as a function of the geography and the CV. The rows give the geographic area of the estimate while the columns indicate the resulting level of accuracy in terms of the CV, given the size of the estimate. To determine the CV for an estimate of size X in an area A, look across the row for area A, find the first estimate that is less than or equal to X. Then the title of the column will give the approximate CV. For example, to determine the sampling error for an estimate of 35.4 thousand unemployed in Newfoundland and Labrador in August 2011, we find the closest but smaller estimate of 25.2 thousand giving a CV of 5%. Therefore, the estimate of 35,400 unemployed in Newfoundland and Labrador has a CV of roughly 5%.
Table 7.1 is supplied as a rough guide to the sampling variability. The sampling variability is modeled so that, given an estimate, approximately 75% of the actual CVs will be less than or equal to the CVs derived from the table. There will, however, be 25% of the actual CVs that will be somewhat higher than the ones given by the table.
Table 7.1 can also be used with either seasonally adjusted estimates, or with estimates that have not been seasonally adjusted. Studies have shown that LFS standard errors for seasonally adjusted data are close to those for unadjusted data.
The CV values given in table 7.1 are derived from models based on LFS sample data for the 47-month period from January 2008 through November 2011 inclusive. It is important to bear in mind that these values are approximations.
Variability of annual estimates
To look up an approximate measure of the CV of an estimate of an annual average, please consult table 7.2, which gives the size of the estimate as a function of the geography and the CV. The rows give the geographic level of the estimate while the columns indicate the resulting level of accuracy in terms of the CV, given the size of the estimate. To determine the CV for an estimate of size X in an area A, look across the row for area A, find the first estimate that is less than or equal to X. Then the title of the column will give the approximate CV. For example, to determine the sampling error for an annual average estimate of 32.7 thousand unemployed in Newfoundland and Labrador in 2011, we find the closest but smaller estimate of 16.9 thousand giving a CV of 2.5%. Therefore, the estimate of 32,700 unemployed in Newfoundland and Labrador has a CV of roughly 2.5%.
Table 7.2 is supplied as a rough guide to the sampling variability. The sampling variability is modeled so that, given an estimate, approximately 75% of the actual CVs will be less than or equal to the CVs derived from the table. There will, however, be 25% of the actual CVs that will be somewhat higher than the ones given by the table.
The CV values given in table 7.2 are derived from a model based on LFS sample data for the 5-year period from 2007 to 2011. It is important to bear in mind that these values are approximations.
Sampling variability tables for the territories
The CV values given in table 7.3 for the Yukon and Northwest Territories are derived from models based on LFS sample data for the 48-month period from December 2006 through November 2010 inclusive. For Nunavut, they are based on LFS sample data for the 48-month period from January 2008 through November 2011 inclusive.
For more accurate measures of variability, please contact Statistics Canada's National Contact Centre (toll-free 1-800-263-1136; 613-951-8116; infostats@statcan.gc.ca), Communications Division.
Variability of rates
Estimates that are rates and percentages are subject to sampling variability that is related to the variability of the numerator and the denominator of the ratio. The various rates given are treated differently because some of the denominators are calibrated figures that have no sampling variability associated with them.
Unemployment rate
The unemployment rate is the ratio of X, the total number of unemployed in a group, to Y, which is the total number of participants in the labour force in the same group. Here the group may be a province or CMA and/or it may be an age-sex group. For example, in September 2010, there were approximately 34,800 unemployed persons in Newfoundland and Labrador and 259,500 participants in the labour force, giving an unemployment rate of 13.4%.
The CV for the unemployment rate can be estimated with the following formula:
[CV(X/Y)]2 = [CV(X)]2 + [CV(Y)]2– 2p[CV(X)] [CV(Y)]
where CV(X) would be the CV for the total number of unemployed in a specific geographic or demographic subgroup and CV(Y) would be the CV for the total number of participants in the labour force in the same subgroup. The correlation coefficient, denoted p, mesures the amount of linear association between X and Y (respectively, the number of unemployed and the number of participants in the labour force in the same subgroup). The value of p ranges between -1 and 1. For example, a strong positive linear association would indicate that unemployment counts generally increases as the total number of participants in the labour force increases. Note that we can expect a larger CV for the unemployment rate when p is negative since in this case, the third term on the right side of the equation above becomes positive.
When p is not available, the most conservative approach is to take p = -1, which leads to the simplified formula:
CV(X/Y) = CV(X) + CV(Y)
Note that this will likely lead to an overestimation of the CV(X/Y).
In the previous example, the CVs of the monthly estimates for the unemployment count and the total number of participants in the labour force in Newfoundland and Labrador are respectively 5% and 1.0% from Table 7.1. An approximation of the CV for the unemployment rate of 13.4% using the above formula would be:
5.0% + 1.0% = 6.0%
Participation rate and employment rate
The participation rate represents the number of persons in the labour force expressed as a percentage of the total population size. The employment rate is the total number of employed divided by the total population size. For both the above rates, the numerator and the denominator represent the same geographic and demographic group.
For Canada, the provinces, CMAs and some age-sex groups the LFS population estimates are not subject to sampling variability because they are calibrated to independent sources. Therefore, in the case of the participation rate and the employment rate of these geographic and demographic groups, the CV is equal to that of the contributing numerator.
Subgroups of Canada, the provinces and age-sex groups are called domains; for example, persons employed in agriculture in Manitoba are a domain. To determine the CV of rates in the case of domains, the variability of both the numerator and the denominator have to be taken into account because the denominator is no longer a controlled total and is subject to sampling variability. Therefore, for participation rates and employment rates of domains, the CV can be determined similar to the unemployment rate. The totals in the numerator and denominator for the relevant rate should reflect the same domain or subgroup.
Variability of estimate of change
The difference of estimates from two time periods gives an estimate of change that is also subject to sampling variability. An estimate of year-to-year or month-to-month change is based on two samples which may have some households in common. Hence, the CV of change depends on the CV of the estimates for both periods and the sample overlap, p, between the periods. The following formula can be used to approximate the estimate of change:
where Y1 and Y2 are the estimates for the two periods. The value of p is the correlation coefficient between Y1 and Y2. The value of p ranges between -1 and 1, with 1 being the perfect positive linear association. One can generally use the sample overlap to approximate the correlation coefficient as follows:
- For the provinces: use p = 5/6 for month-to-month changes, and p = 0 for year-to-year changes.
Empirical studies at Statistics Canada have shown that for the provinces, a p value equal to 5/6 is a good approximation for estimates of employment, but for estimates of unemployment, a p value of 0.45 would yield a better approximation for month-to-month changes.
When comparing the annual averages of two years, the CV of the annual estimates (table 7.2) should be used. For month-to-month change, seasonally adjusted estimates should be used in conjunction with the CVs of the monthly estimates from table 7.1. Note that the above formula gives approximate estimates of the sampling variability associated to an estimate of change.
Guidelines on data reliability
Household surveys within Statistics Canada generally use the following guidelines and reliability categories in interpreting CV values for data accuracy and in the dissemination of statistical information.
Category 1 - If the CV is ≤ 16.5% - no release restrictions: data are of sufficient accuracy that no special warnings to users or other restrictions are required.
Category 2 - If the CV is > 16.5% and ≤ 33.3% - release with caveats: data are potentially useful for some purposes but should be accompanied by a warning to users regarding their accuracy.
Category 3 - If the CV > 33.3% - not recommended for release: data contain a level of error that makes them so potentially misleading that they should not be released in most circumstances. If users insist on inclusion of Category 3 data in a non-standard product, even after being advised of their accuracy, the data should be accompanied by a disclaimer. The user should acknowledge the warnings given and undertake not to disseminate, present or report the data, directly or indirectly, without this disclaimer.
Release criteria
Statistics Canada is prohibited by law from releasing any data which would divulge information obtained under the Statistics Act that relates to any identifiable person, business or organization without the prior knowledge or the consent in writing of that person, business or organization. Various confidentiality rules are applied to all data that are released or published to prevent the publication or disclosure of any information deemed confidential. If necessary, data are suppressed to prevent direct or residual disclosure of identifiable data.
The LFS produces a wide range of outputs that contain estimates for various labour force characteristics. Most of these outputs are estimates in the form of tabular cross-classifications. Estimates are rounded to the nearest hundred and a series of suppression rules are used so that any estimate below a minimum level is not released.
The LFS suppresses estimates below the levels presented in the table 7.4.
- Date modified: