Reports on Special Business Projects
Measuring remoteness and accessibility: A set of indices for Canadian communities
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
by Alessandro Alasia, Frédéric Bédard, Julie Bélanger, Eric Guimond and Christopher Penney
User Information
Acknowledgments
The authors would like to acknowledge the insights and feedback provided by many people over the course of this project. Pierre Gauvin, Eric McGregor (Aboriginal Affairs and Northern Development Canada - AANDC), Michael Savage and Rene Dion (Health Canada) were instrumental in launching this project and moving it through completion. Peter Murphy and Rob Cunningham (Statistics Canada) provided valuable comments to earlier drafts of this report. Valuable feedback and suggestions were gathered at various meetings and conference calls with Health Canada and AANDC staff in Ottawa and the regional offices.
Summary
Proximity to centres of economic activity and population agglomerations is an important determinant of regional socioeconomic outcomes and, consequently, a relevant factor in the analysis and delivery of policies and programs. For this reason, measures of remoteness and accessibility have been used by various departments for years. Some of the existing indices were developed in the 1980s and have been used since with only minor revisions.
This study was undertaken in response to the need to update and upgrade the current measures of remoteness. The objective was to conceptualize and implement a method that takes into account the most recent literature on the subject, as well as taking advantage of new computational opportunities provided by the integration of official statistics with data from non-official statistical sources.
The focus of the analysis was on the concept of “remoteness” and, consequently, on the creation of an index of remoteness for Canadian communities. However, through the process of developing the index and testing for alternative specifications it was felt that a set of accessibility measures to selected services computed with a similar methodology could provide further information for specific research and policy purposes. Furthermore, it was found that the comparison of accessibility measures with the remoteness index implemented in this analysis provided support to the view that the latter could serve as a good proxy for service accessibility.
As a result, this report outlines the methodology for an index of remoteness and a set of accessibility measures to selected services. For both concepts, the underlying approach is based on the principle of a gravity model, in which both the proximity to and the size of the population (or service) agglomerations are accounted for. The computational model accounts for the community’s proximity to multiple points of service provision within a given radius that allows for daily interaction. The indices are computed for all communities (census subdivisions) which reported some population in 2011 (or were connected to the main road network); they are presented in a continuous form, with values ranging from 0 to 1, which can be converted into any categorical grouping.
For the index of remoteness, the population size of the population centresNote 1 is used as a proxy of agglomerationNote 2 and general measure of service availability. The methodology and results presented in this report highlight one of the main challenges for the computation of a continuous index, which is the identification of a common measure of “distance” for communities with substantially different transportation infrastructures. Network distance and travel time do not provide an adequate measure of proximity when comparing communities having no or limited access to the road network, with those connected to the main road network. The only meaningful measure of proximity to generate a continuous index for all communities is travel cost. For communities connected to a population centre through the road network, the travel time was generated using the Google Maps Application Programming Interface (API) and converted to travel cost using coefficients of conversion. For communities that were not connected to the main road network, travel cost was generated from an ad hoc database of least expensive travel options, for individuals, to the most accessible population centre.
The set of accessibility measures is presented in this report mainly for illustrative purposes, as their analysis show that they are generally highly correlated with each other and with the remoteness index. This supports the expectation that population size can be used as a proxy for the availability of services. The method used to compute these measures is based on the same gravity model principles that were used for the remoteness index, with two differences: (1) travel time is computed from census subdivision (CSD) to CSD, instead of CSD to population centre; and (2) total revenue by CSD for selected business types accounts for the availability and size of services, instead of population size. Total revenue data are taken from the 2012 Business Register. These measures, or similar variations of these measures, could be used to fine-tune the remoteness index or to discriminate between degrees of remoteness in extremely remote locations.
Introduction
Proximity and agglomeration have been long recognized as important factors in shaping the socioeconomic opportunities of regions. Even in a globalized world, in which transportation and communication technologies have altered the meaning and perception of distance in many ways, geographic proximity remains a well established determinant of socioeconomic outcomes at the local level.
For this reason, various operational measures of proximity have found widespread use in applied research and policy analysis. Among the most prominent examples are measures of remoteness from economic activities or, conversely, the accessibility of economic activities. In broad terms, these measures are intended to represent the potential disadvantages which may be associated with distance from the points of service provision and/or the lack of agglomeration. These types of measures have been used in policy analysis and program delivery to assess, and possibly compensate for, the conditions associated with a specific geographic location.
Although various measures have been developed at the local or regional level, in the Canadian context no methodology and measure exist that are applicable to all communities across the country. This research is intended to fill this gap. This paper presents the computational methodology and the results of an index of remoteness created for all Canadian communities (census subdivisions) reporting some population in the Census year 2011 or connected to the main road network.
In conjunction with this index, we also present the methods and results for a set of measures of accessibility to selected services. Although the main focus of this research project was on an index of remoteness, the conceptual and methodological development of such an index for the Canadian context led to the specification of a set of ancillary measures of accessibility to selected services.
The methodology proposed in this paper addresses the computational challenges of implementing a general model for the computation of the indices, which hinges on the principle of a gravity model and uses measures of distance and agglomeration as key inputs. In spite of the relative complexity of the computations the model relies on a transparent and intuitive approach, which can be easily communicated to users and updated over time. It also makes a parsimonious use of input data, organized in a matrix of proximity measures and a vector of population (for remoteness) or business (for accessibility) agglomeration measures. The results show the high correlation between the two sets of measures (remoteness and accessibility), lending support to the general perception that population counts represent a reasonable approximation for accessibility to basic services across Canada.
The methods adopted in this analysis demonstrate the potential of combining data from official statistical sources with data from non-official statistical sources, for statistical and analytical purposes. Specifically, the framework uses census data and microdata from the Business Register in combination with travel time matrices generated from the Google Maps API. Although distance matrices could be generated using official statistical sources, for this specific application the use of non-official statistics proved to be a more suitable and flexible approach.
The paper is organized as follows. After this introduction, the second section summarizes the literature on the subject, with a focus on applied indices used in various research domains. The third section presents the concepts, the methods, and the data sources used in the analysis. The fourth section presents the results of the index of remoteness and a set of accessibility measures to selected services. Finally, the last section concludes with considerations about the potential development of the current model and applications to other domains.
Review of the literature and existing applications
The concepts of remoteness and accessibility have been used in various research domains, resulting in a diversity of conceptual and methodological approaches and no single and predominantly accepted definition in the literature. As a result, it is particularly challenging to assess the alternative methodological options that could be applied to the Canadian context.
The disciplinary domains in which the remoteness and accessibility literature can be found include geography, economics, health studies, transportation studies and, more broadly, social studies on population disadvantage and deprivation. There are, however, three considerations that helped in navigating through this literature.
First, the concepts of remoteness and accessibility have been used in close relationship, in some cases being treated as synonymous and in other cases being viewed as two faces of the same coin. However, if a distinction can be made between the two concepts, it appears fair to say that “remoteness” has been used in broader and more general terms to identify isolation in physical terms, while the concept of “accessibility” has been used predominantly in social research to assess availability of services and the barriers to access services, often at the individual level. The concept of accessibility is always qualified as access to something; thus, the concept of accessibility is used to capture the possibility of access as determined by geographic proximity.
Second, there appears to be a continuum of methodologies for the measurement of both remoteness and accessibility, ranging from relatively simple measures to more complex methods that apply multivariate analysis or a mix of qualitative and quantitative methods.
Third, although there is no perfect overlap between disciplinary domain and methodological approach, there appears to be prominent methodologies which recur within each disciplinary domain.
Therefore, at the risk of oversimplification, in this concise review we present the predominant methodological approaches within each disciplinary domain and some of the main characteristics of these methodologies.
Although spatial analysis is the underlying theme of virtually all research on remoteness and accessibility, geography is unquestionably the disciplinary domain which is at the core of most of this literature. The geographic emphasis has been on remoteness as physical isolation and distance from agglomerations.
The geographical approach has generally defined remoteness in terms of environmental parameters that influence access, such as physical remoteness from population centres or geographic parameters that influence access to services (Dunne et al. 1999). In this literature, remoteness is defined in terms of geographic distance separating a spatial unit (community, census tract, etc.) from nodes of activity. The major focus is on how distance restricts opportunities for interaction. Hence, the concept of “remoteness” is generally associated with the physical isolation of a community or region.
The most prominent examples of this type of research at the national level are the Australian indices of remoteness and accessibility. Currently, there are three variations of remoteness measures that are applied at the national level in Australia: the Rural Remote and Metropolitan Areas classification (RRMA), the Accessibility/Remoteness Index of Australia (ARIA), and the Australian Standard Geographical Classification (ASGC) (AIHW, 2004). The underlying assumption of these classifications is that remoteness can be interpreted in a geographical manner as access to a range of “services”.Note 3
The RRMA classification is the oldest of the three, developed in 1994, and is still used for research, policy and funding purposes (DHA 2005 and 2009). This classification uses population size and calculated direct distance from the nearest service centre to determine seven discrete categories. The definition of service centre is based on population size parameters, with the lowest threshold value for a service centre being set at 5,000 people.
The ARIA (Accessibility/Remoteness Index of Australia) is a slightly more recent development, released in 1997. It created a classification of localities based on a continuous measure of remoteness (index score) and used a finer geographic resolution compared to that of the RRMA. The index score was computed on the basis of minimum road distance from any inhabited point to the nearest service centre, which was defined as an urban area with a population of 5,000 or more. To assess service delivery, the service centres were grouped into four population classes; the population size of the service centre is used as proxy for the availability of services. The index scores were grouped into 5 categories, defined as highly accessible, accessible, moderately accessible, remote and very remote.
The ASGC (Australian Standard Geographical Classification) Remoteness classification was released in 2001 based on an enhanced version of the ARIA index, named ARIA+ (AIHW, 2004). A number of technical improvements were introduced, although the main conceptual apparatus on the measure, based on minimum road distance to a service center, remained similar.
The economic literature that relates to the analysis of remoteness highlights the difference between that concept and the mere concept of distance. In economic analysis the emphasis is on a measure of distance from multiple centres of economic activity (consumer markets and suppliers), with most of this literature being found in the field of international trade (Battersby and Robert 2005). The literature on international trade has incorporated remoteness into modeling to assess its impact on trade flows and trade barriers. In this type of economic modeling literature, the concept of remoteness has been used as a generalization of the concept of distance (Battersby and Robert 2005; Duran Fernandez 2008). As a result, the measure of remoteness is not a measure of distance for a country pair, but rather a multilateral analogue that measures the overall distance of one country from its potential trading partners (Duran Fernandez 2008).
In practice, the indices developed in this literature are defined as being an average of the distance from each country to all other countries, weighted by the reciprocal of GDP, so that the measure of remoteness captures the potential strength of a country’s economic ties with the rest of the world (Frankel and Romer 1999; Battersby and Robert 2005). For instance, Borgatti (2008) uses remoteness in the context of bilateral trade research. Remoteness is defined as the average weighted distance between any two countries with weights reflecting the absorptive capacity of the partner country.
The technical specifications used in this literature vary to some extent. Girma and Yu (2002) use a remoteness index (R) that, for country i, is defined as the ratio between a distance between country i and country j and the GDP of country j (for all j not equal to i). By contrast, Evans and Hughes (2003) use a similar specification in which the remoteness index (R) is defined as being the summation of the ratios of GDP to distance (for all j not equal to i), plus the ratio of GDP of country i divided by a measure of internal distance.
In economic literature, the concept of remoteness has also been applied in micro-economic analysis of households’ economic disadvantage. In this literature, remoteness is used as a potential determinant of socio-economic outcomes and is conceptualized primarily as distance and isolation, which manifests itself in the form of high transaction costs, such as the cost of transporting a product to major market centres, and with an implicit recognition that the degree of isolation can be ameliorated through public interventions such as infrastructure development and/or the provision of public goods (Wu and Gopinath 2008).
As an example, Stifel et al. (2003) examine the relationship between remoteness (isolation) and economic disadvantage in Madagascar, using household and community level data. These authors noted that distance to urban centres or markets is generally the measure of choice for isolation; in their analysis they expand this measure with a remoteness index created from a factor analysis of various isolation measures collected by a census: distances to health facilities, banks, post offices, schools, taxis, courts, input markets, agricultural extension services, veterinarians, access to national or provincial roads, public services, media, various markets, and various measures of access to transportation.
Another major stream of relevant literature is found in health studies; here, the emphasis is on the concept of accessibility and specifically on accessibility to health services for communities and/or individuals. Wakerman and Humphreys (2008) review several definitions related to remote (and/or rural) health practices, generally defined as practices in communities beyond a certain distance (or specific travel time) from specific services. Various indices of accessibility have been proposed in the literature; one of the common feature of these indices is that each measures access to a specific type of service (e.g. access to hospitals, medical doctors, etc), which leaves largely unanswered the question of combining the accessibility of qualitatively different services into a single measure. One early example is the work of Simon et al. (1979), who developed an index to measure accessibility to health services provided on an outpatient basis at a specific health centre (the Kaiser Community Health Foundation, Cleveland, Ohio).
Luo and Wang (2003) also developed a method to assess accessibility to health services that became a point of reference in this literature. This method, named the two-step floating catchment area (2SFCA), was developed in a GIS environment and measured spatial accessibility as a ratio of primary-care physicians to population. The method computed the ratio of suppliers to residents within a service area centred at a supplier's location and summed up the ratios for residents living in areas where different providers' services overlap. This method inspired further work, with other authors either extending the method into an enhanced version of the two-step floating catchment area (Luo and Qi 2009) or creating variations of it (McGrail and Humphreys 2009). More recently, the OECD (2012) reviewed a number of possible measures of access to hospitals, which rely on a measure of density of the service in a given region or driving time to the closest (single point of provision) hospital facility.
Similarly to health studies, transportation studies is another disciplinary domain in which literature on measures of accessibility to transportation facilities can be found; in this case, the focus on the accessibility measure is for a specific type of service, namely transportation services (Bhat et al. 2002; Pooler 1995). The focus of this analysis is often on people’s opportunities (i.e. accessibility) to reach commonly used services, motivated by the consideration that greater accessibility of public transport systems could contribute to a more sustainable transport system.
At a broader level, a review of some of the concepts and possible indicators of accessibility for a broad range of services was conducted by the OECD (2014). Also in this case, the report points to a variety of different measures at the local level, all of which could provide information on a specific dimension of accessibility but none of which would provide a general measure of remoteness or accessibility to services.
Concepts, methods, and data sources for the Canadian context
This section presents the methodology established to compute a Canadian index of remoteness and an ancillary set of accessibility measures to selected services. One of the main challenges in the development of these indices was to strike the right balance between the needs of a potentially broad group of users, on the one hand, and the technical constraints dictated by computational complexity and data limitations, on the other hand. For this reason a set of guiding principles for the index developed were articulated and made explicit; these guiding principles are summarized below.
It should be emphasized once again that the focus of this research was on the concept and measurement of remoteness. The concept and measurement of accessibility to services took shape over the course of the study as an inherently intertwined but nonetheless separate conceptual dimension, which deserved a separate set of measures. For this reason, most of the concepts and methods described in this report are focused on the index of remoteness.
Over the course of the analysis several alternative specifications of each index and measures were tested, using several threshold values for the key parameters.Note 4 The goal was to gain a better understanding of the sensitivity of the results to alternative specifications and threshold values.
Guiding criteria for the design of the indices
Using the insights generated from the literature review and discussions with potential users, a set of desirable features and specification criteria were identified in order to select the most suitable methodological approach.
Three features were set as requirements for an index of remoteness:
- First, the index was expected to ensure coverage of all Canada at a detailed geographic scale;
- Second, the index was envisioned as a continuous measure, as opposed to categorical measures;
- Third, the focus on the “remoteness and accessibility” concepts used for the index was limited to that of physical proximity, as opposed to other dimensions that are intended to capture economic, social and cultural barriers or distances.
With regard to the conceptual strength of the indices, it was felt that methods that accounted for proximity to multiple points of service provision (or agglomeration), as well as the different population sizes of these multiple points, presented a conceptual advantage and were more suitable to the Canadian geography than methods that accounted for proximity to a single point of service provision (or agglomeration). As a result, methods based on a gravity model approach were preferred.
At the same time, the transparency of computational methods was regarded throughout the project development as a positive attribute. For this reason, approaches that required combining qualitatively different measures (e.g. different types of services) into a single indicator by using expert judgment, weighting schemes, or more complex statistical methods such as data reduction techniques or multivariate analysis, were avoided. The rationale behind this decision was the recognition that overly complex computations might have implications for the computation itself, for the ease of maintenance of the index, and - most importantly - for the potential interpretability of the index values by users.
A parsimonious use of input data was also considered to be a desirable attribute for the index, in view of the potential for future updates and possible adaptations of the index. Therefore, specifications that make use of a relatively contained set of variables were favoured, over more complex specifications resulting from multivariate analysis.
Finally, consideration was given to the ease and cost of maintenance of the index in the future. The desired result was to generate an output whose update would require a relatively simple process of updating key datasets and re-running program codes, based on input data updated at regular intervals and easily accessible at relatively low costs, as well as fully documented program codes.
Geographic definitions
Given the data requirements and the intent to develop a measure that would cover the entire country at a small geographic scale, the most suitable geographic unit was the census subdivision (CSD). The CSD is an administrative geography that is a municipality or an area that is deemed to be equivalent to a municipality for statistical reporting purposes (e.g., an Indian reserve or an unorganized territory).Note 5 Because of this correspondence with an administrative entity (the municipality), CSDs are the most commonly used territorial units for indicators that are intended to be used in policy analysis or program delivery at the local level.
The boundary file of CSDs is updated for each census cycle, occurring once every five years. This analysis is based on the most updated version, that is, the 2011 census boundary file which divides the entire land area of the country into 5,253 CSDs. The index and measures presented in this report are implemented for all CSDs of Canada reporting some resident population in 2011 or connected to the main road network. This resulted in an index value for 5,211 CSDs.
Given the emphasis on the concept of service centre found in the literature and existing applications, a second geographic concept was used in the computations of the index of remoteness; this is the concept of the population centre (PopCtr). A population centre is defined as an area with a population of at least 1,000 and a density of 400 or more people per square kilometre.Note 6 Hence, the computation of the index of remoteness entails the combination of the CSD geographic layer with the population centers geographic layer. For practical purposes, the accessibility measures were computed using only the CSD geographic layer, as discussed in more detail below. It should be emphasized that all the results are tabulated at the CSD level, while PopCtr level data and geographic layer are used only for computational purposes.
For the purpose of this analysis, CSDs can be distinguished as being one of two types: units connected to a population centre through the national road and ferry network, and units that are not connected to a population centre through the national road and ferry network. This distinction has major methodological implications for the way in which proximity between units can be measured, as will be discussed in the following section.
Map 1 highlights the geographic locations of CSDs with different types of transportation infrastructures, specifically those that are connected and those that are not connected to the main road network (grouped into three broad categories). There are 149 CSDs that had population reported in 2011 and were not connected to a population centre through the main road or ferry network.Note 7 Some of these geographic units can only be reached by air transportation, while others can be reached by a combination of transportation means, including regular flights, charter flights, railway, regular ferry or charter boats. For the purpose of this analysis, any CSD which did not have full year-round access to a population centre through the main road network was flagged as community not connected to the main road network.
Map 1 Communities and type of transportation infrastructure (connected versus not connected to the main road network), Canada

Description for Map 1
Proximity: representative points and unit of measure
At the core of this analysis are the methods that were used to define and measure “proximity”. Even though the focus of this analysis is restricted to the concept of spatial proximity, there are multiple units of measures that could be used (including network distance, travel time and travel cost). In addition, various options could be used in order to identify the representative points from which distance can be calculated. The methods used in the present analysis are detailed below.
Representative point for a CSD
Measuring geographic proximity requires turning a continuous and two-dimensional geographic surface into a set of discrete points from which distance can be measured. This was done by establishing representative points for each geographic unit used in the analysis; that is, for each population centre and CSD.
The most straightforward method through which to define a representative point in a given geographic area is to generate geographic centroids, located at the geographic centre of a polygon representing the area. This method was used for the identification of the representative points of population centres, which are by definition areas with a relatively high population density and relatively small land area.
However, for larger administrative units and especially for large CSDs, a geographic centroid can potentially be located far away from where most of the population resides and likewise distant from transportation infrastructure, which in turn might lead to substantial misrepresentation of a distance measure. For this reason, as a general rule the representative point for each CSD has been located in the most populated area of the CSD, always near a major road, while for CSDs not connected to a population centre through the road network the location of railway stations, sea ports, or airports was considered in a similar fashion.
More specifically, the methodology for the calculation of the representative point can be presented by the following three typical cases.
The first case is comprised of CSDs with one or more population centres, or areas with a large density of population and dwellings (> 400 people/km2) and above a minimum size (population of at least 1,000). For this type of CSD, the representative point is placed in the centre of the largest population centre of the CSD. This point is located no more than 100 metres from a major road or highway. An example of this case is shown in Map 2, representing the city of Gatineau, Québec.
Map 2 Example of representative point: CSD type 1
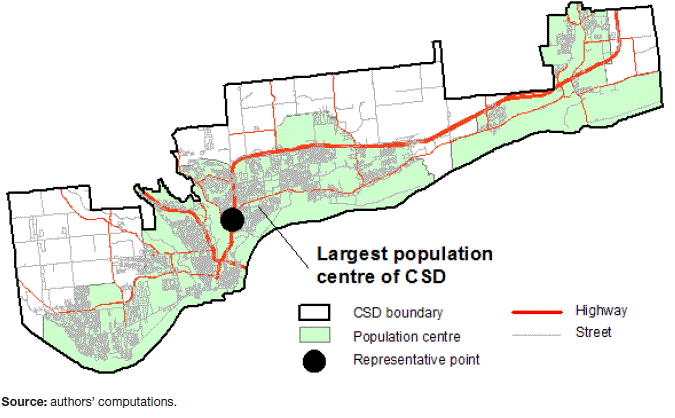
Description for Map 2
The second case consists of CSDs with one or many small dwelling clusters (between 100 and 400 people/km2), none of which reach the thresholds of a population centre.Note 8 For this type of CSD, the representative point is placed in the centre of the largest cluster of population, no more than 100 metres from a major road or highway. An example, shown on Map 3, is provided for the CSD of South Glengarry, Ontario (with a total population of 13,162 in 2011 and an average population density of 22 people/km2).
Map 3 Example of representative point: CSD type 2

Description for Map 3
The third case consists of CSDs that do not have any population clusters. In very remote areas, some CSDs have no permanent population, or are composed of populations that are sparsely distributed with a population density of less than 100 people/km2. For this type of CSD, the representative point is placed at the geographic centre of the polygon, no more than 100 metres from a major road or highway. If there are no roads in the CSD, the point is placed near an airport, railway station or sea port.Note 9 Map 4 illustrates the example of the CSD of Squamish-Lillooet A, British Columbia (with a total population of 224 in 2011, and an average population density of 0.1 people/km2).
Map 4 Example of representative point: CSD type 3
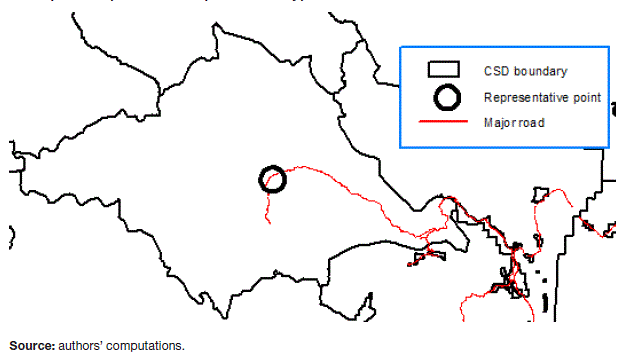
Description for Map 4
Unit of measure of distance
Proximity is measured between the representative points of each territorial unit. Three units of measures were considered: network distance, travel time, and travel cost. In order to generate a continuous index of remoteness for all CSDs, travel cost was used as a common metric of proximity. The rationale behind this choice and the methods used for the computation are presented in this section.
If all communities had the same type and quality of transportation infrastructure (typically, road accessibility), the unit of measure would be virtually irrelevant for the purpose of this analysis. Distance could be expressed in any unit of measure and a conversion to other units of measure would be, to a large extent, a matter of functional transformation using representative coefficients of conversion.
In reality, the type and quality of transportation infrastructure vary substantially across CSDs. The main divide is between communities that are connected to a population centre through the road network (or regular ferry) and communities that are not connected through the road network (typically fly-in communities).
For communities that have similar transportation infrastructures and are connected to a road network, both network distance and travel time provide an acceptable approximation of proximity. However, testing suggested that travel time provides a more accurate representation of proximity, particularly when the shortest (or unique) route encompasses the use of ferries or different qualities of roads.
For example, if the proximity between representative points of Ottawa and Montréal is measured by network distance on the road network (using Google Maps API) the result is 195 km; the corresponding travel time is 2 hours and 12 min (average speed of 88.6 km/h). In the case of Vancouver to Victoria, the network distance is 106 km, while the travel time is 2h 54min (average speed of 36.6 km/h, which takes into account the ferry section). Thus, travel time provides a more accurate representation of the actual “distance” between communities for the purpose of the present analysis.
Travel time, however, does not represent a viable option to compare communities that have major differences in transportation infrastructure; specifically, road connected versus non-connected communities. In these cases, travel time might provide misleading results. A fly-in community may be less than two hours from a major population centre; however, the cost of reaching that community is not comparable with the cost of reaching a similar community at a two hour drive distance from the same population centre. Means of transportation makes a major difference in terms of opportunities and potential socioeconomic outcomes.
Since the index of remoteness was intended to reflect the socioeconomic conditions of a community, travel cost was used as a common metric of proximity for all CSDs in Canada. The calculations of travel costs used in this analysis are based on the cost for one individual traveling between two locations using the most accessible and less expensive travel option. All travel time values were converted to a cost for communities connected to a population centre through the road network, and individual travel costs for communities not connected to a population centre through the road network were retrieved from various sources.Note 10
For CSDs that have one or many population centres accessible by road or regular ferry, the travel duration is converted to cost using the average cost of driving a vehicle in Canada (Canadian Automobile Association, 2012)Note 11. The value of $0.17 per km is based on the average annual operating costs (including fuel) of an average-sized car traveling 18,000 km per year. Using travel time results from the Google Maps API, at an average travel speed of 80 km/h this corresponds to $13.60 per travel hour. A 200 km or 2.5 hour threshold was set as limit for accessing services on a daily basis, which converted in cost for traveling by road, corresponds to $34.00 ($13.60/hour * 2.5 hours).
For CSDs not connected to a population centre through the road network or regular ferry services, alternative travel options were sought. As a first step, each of these CSD was categorized based on available travel options. Along with each travel option, the closest and/or most accessible population centre was also selected. The cost for one individual traveling one-way, including taxes, was extracted for options commercially available. For segments that had more than one option available (e.g. by train or by air, or by air by two or more different companies), the option with the lowest cost was selected.
Some CSDs with small populations do not have any regular service (air or boat). For these cases, air or boat services have to be chartered. Instead of obtaining all charter cost options by air, information that is generally not available online, a straightforward linear model was used to convert linear distances into costs. The model was computed using the cost/km incurred by a set (n=184) of not connected CSDs that had regular air service to a population centre (costs obtained as of January 2013). For example, the cost between CSD x and POPCTR y, that are 300 km apart (linear distance), was estimated at $273 using the linear equation: cost = 0.7684 * km + 42.178. These costing computations might be further refined in specific applications or for specific cases, as more detailed information is reported or as transportation conditions changes on the ground.Note 12
Input data: official statistical sources
Two main sources of official statistics are used in this analysis. Population counts from the census are used to generate the index of remoteness; and business microdata from the Business Register are used to compute the accessibility measures.
The total population size of population centres in 2011, published by the Census of Population 2011, is one of the key input data in the computation of the remoteness index.Note 13 However, it should be mentioned that supplementary population information was used for thirty-one (31) CSDs which were incompletely enumerated in the 2011 Census of Population. Alternative sources of information for population counts were used, including the Registered Population counts as published in the First Nation Profiles of the AANDC website, 2006 Census of Population counts, Affaires Municipales, Régions et Occupation du Territoire, Québec, communities’ websites and published studies from diabetes prevention program or environmental assessment projects.Note 14
For the computation of the accessibility measures, the presence of services is measured with data from the Business Register (BR).Note 15 The BR serves as a central data source for a consistent and well maintained inventory of businesses with national coverage. Establishments in the Business Register are coded based on the concept of major business activity using the North American Industry Classification System (NAICS).
For the purpose of this analysis, the 2012 version of the Canadian NAICS was used. Selected NAICS codes were used to identify the services of interest in the analysis. The spatial coding of the establishments is based on the standard geographical classification maintained by Statistics Canada. The link between a specific establishment and its location is made using an address, a postal code and/or the Census subdivision identifier
In addition to these two data sources, the Road Network file (created as of census year 2011) was used in the determination of the representative points for census subdivisions, as illustrated in the previous section. These files are digital representations of Canada's national road network and are available free of charge on the web page of Statistics Canada.Note 16
Input data: non-official statistical sources
The travel distance and the travel time were calculated by the Google Maps Distance Matrix API; Google Maps maintains a road network for Canada and the rest of the world that forms the basis for network distance and travel time calculations between an origin and a destination. The road network is also classified based on road type, speed limit and type of surface. The network includes ferries with regular service to connect communities on islands with the main network.
For the purpose of this analysis, the use of the Google Maps Distance Matrix API proved to be a more effective source of information than the Road Network file maintained by Statistics Canada. Submission to the API of batches of geographic coordinates for pairs of representative points was done through Python coding.Note 17 The API returned travel time and travel distance for each pair of coordinates. As discussed in the previous section, the travel time proved to give a more accurate measure of proximity because it accounted for differences in the quality of the road network and the possible presence of parts of the itinerary in which ferries must be used, thus, where the average speed is much lower than on roads.
The set of CSD to PopCtr pairs within the 200 km threshold required the calculation of approximately 250,000 travel durations and distances, with the complete distance matrix for all pairs consisting of approximately 5 million data points. The set of CSD to CSD travel durations and distances within the 300 km threshold required the calculation of approximately 2.4 million data points, with the complete CSD-to-CSD distance matrix consisting of approximately 14 million data points.
The travel time obtained from Google Maps Distance Matrix API represents a key input parameter for the computation of the proximity measure. In addition, other non-official statistical sources were also used. The data on transportation infrastructure were compiled from the Canada Flight Supplement, NAVCanada, November 2010 version. Data on transportation cost for communities not connected to the main road network were collected from various internet websites providing flight costs or cost of regular ferries.Note 18
Computational model
The computational model began with the specification of a general model, which builds on the principle of a gravity model and accounts for the possibility of multiple points of connectivity and service provisions.
The general measure of remoteness/accessibility (RA) for the reference point i can be expressed as the summation of an agglomeration size at the point of provision (Ak) divided by a distance measure (D) between the reference point i and the point of provision k; for all D less than or equal to a given threshold value (x); and an assumed minimum distance value (z), in cases where the representative point and point of provision are the same. In mathematical terms:
(1)with the following conditions:
The computational model was implemented in SAS and documented program files are available from the authors upon request. Following the approach of this general specification, the following specifications and threshold values were used to compute the index of remoteness and the accessibility measures.
Index of remotenes
The remoteness index of a CSD is determined by two key parameters: (1) the proximity to all population centres (PopCtr) within a given radius that permits daily accessibility; and (2) the population size of each population centre, used as a proxy of service availability.
The computational model accounts for all population centres in proximity to the CSD of reference (as opposed to the closest centre of any given population size), because each population centre could be a potential location for services (point of service supply) that could potentially be used by the residents of neighbouring communities.
Following the idea of a gravity model, the remoteness index of community i can be described as the summation of the sizes of the population centres (Pop) that can be reached by community i, divided by a measure of the proximity (travel cost C) of each population centre to community i; for all population centres within a set travel time (T) of 150 minutes, or 2.5 hours, from the community. In formal terms, the following computation model (and associated conditions) is applied:
(2)with the following conditions:
- , for all > 150 minutes; and
- ; if there is no PopCtr with < 150 minutes and i is connected to the main road network;
- = $3if i = k or if < 3.75 minutes.
Condition (a) limits the range of interaction to what is generally the range outside of which the count of daily commuters approaches the zero value. Condition (b) ensures that each of the 255 CSDs that are connected to a population centre through the main road network but which are located more than 150 minutes away from the closest centre would still have one point of connection (that is, the closest population centre). Condition (c) ensures that for each CSD the size of its own population centre is included in the calculation when locations of the two representative points overlap or are very close; the $3 value is assumed to be the minimum representative cost for the purpose of this analysis.
The input data and computations are compiled in a matrix format. Two input matrices are used: (1) Matrix CSD-PopCtr (5,253x942), which contains the travel cost between the representative points of CSDs and population centres; and (2) Vector PopCtr (942), which contains the total population counts of the population centres.
Accessibility measures
The concept of accessibility to services is captured through a set of accessibility measures for selected services and facilities. For these measures, the methodology is similar to that of the remoteness index presented in the previous section, with some notable differences.
Unlike the remoteness index, for which the distance to a population centre is calculated, for the accessibility measure the distance CSD-to-CSD was used. This choice was justified by the fact that the use of PopCtr as a level of geography might have resulted in the exclusion of some businesses located outside the boundaries of population centres, which could have underestimated the supply of services to the neighboring communities. It was generally felt that the geographic accuracy of microdata from the Business register (BR) was more robust at the CSD level than at the level of population centre; hence, the BR data were mapped at the CSD level.
Related to this, and given the specific nature of the measure (access to a specific service), communities that were not connected to the road network, and which did not report any presence of the selected service in their own CSD, were flagged as communities with “no direct access” to the service.
The implication of this specification choice is that, for this specification of accessibility measures, there was no need to estimate travel costs for non-connected communities; thus travel cost would be a plain linear transformation of travel time generated with the Google Maps Distance Matrix API.
The accessibility measures use total gross revenue (TotRev) at the CSD level for specific businesses grouped based on their NAICS code; hence, total revenue is used to measure the presence and size of service provision.Note 19 This measure of agglomeration is divided by the travel time between CSDs (given the specification described above, travel cost would generate the same results), for all CSDs which can be reached within 150 minutes of travel time. In formal terms, using the same notation described for the previous equation, the following computation model (and associated conditions) is applied:
(3)with the following conditions:
- = 0, for all > 150 minutes; and
- ; if there is no PopCtr with < 150 minutes and i is connected to the main road network
- = $3 if i = k or if < 3.75 minutes (or approximately 5 km).
As was done for the index of remoteness, these conditions are set to ensure that: (a) interaction is considered only for plausible daily commuting distances, defined as less than 150 minutes of travel time; (b) if no service is found within 150 minutes travel time, but the CSD is connected to the main road network, the closest CSD that reports revenues for the selected NAICS group is used for the purpose of the computation; and (3) the presence of businesses within the community itself are accounted for in the index, using an imputed proximity value.
This specification of the accessibility measure focuses on the supply side and implicitly recognizes that there might be economies of scale in service provision; looking at medical services, for example, a larger hospital is expected to have more specialized services, equipments, and professionals than a smaller hospital. Likewise, particularly for access to services which are provided by the private sector (e.g. retail), if several options are accessible and there is a critical mass of services in close proximity then the quality of these services is likely to be better than in a situation where only one such service is available.
The input data and computations are carried out within a matrix format. Two input matrices are used: (1) Matrix CSD-CSD (5,253 x 5,253), which includes the travel time between representative points of the CSDs; and (2) Vectors of TotRev (5,253), which include the total gross revenue for specific NAICS groupings at the CSD level.
Rescaling of the value of the indices
The original values of the remoteness index and accessibility measures are rescaled to the range 0 to 1. This is done by normalizing the original values as follows:
(4)It should be noted that for the index of remoteness the zero value corresponds to the minimum value of remoteness and the value of one corresponds to the maximum value of remoteness. For the accessibility measures, conversely, the rescaling results in a value of 0 for the CSD with the lowest value of accessibility and a value of 1 for the CSD with the highest condition of accessibility to a given service.
In order to facilitate the interpretation of the results, when remoteness and accessibility measure are plotted on the same chart, the complement to one of the original accessibility measure value is used (that is, 1 – original value). In this way, the accessibility measure can be reframed to represent lack of access with a value of 0 indicating the CSD with the best conditions of access to the service and a value of 1 indicating the CSD with the most lacking access to the selected service.
Results
Index values were computed for all CSDs of Canada reporting some population in 2011 (or CSD with no population but connected to the main road network), resulting in a database with index values for 5,211 CSDs out of the 5,253 CSD existing in Canada in 2011. This database is available from the authors upon request. The index of accessibility was computed for selected services and illustrative examples of the results that are generated using this methodology are presented below. The same model could be applied to a multitude of service types, as defined by customized grouping of NAICS codes.
The following section presents the statistical and spatial distribution of the index values. In this section, the relationship between the index of remoteness and accessibility measures is also highlighted, as well as the relationship between remoteness index values and some of the standard geographic classifications used in Canada.
Index of remoteness
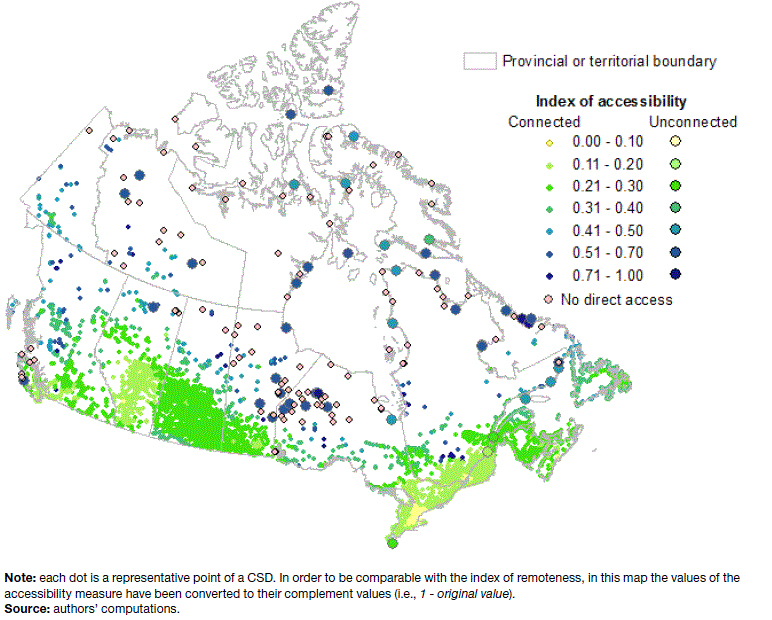
Figure 1 and Figure 2 present the frequency and ranked distribution of the index values for all CSDs for which the index is computed, while Map 5 shows the spatial distribution of the same index values. Each dot on the map represents the representative point for one CSD. In Figure 2, likewise, each point represents one CSD value. In the map, the larger circles indicate communities that are not connected to a population centre through the road network.
It is evident from the map that the spatial pattern quite closely reflects the pattern of metropolitan agglomerations across Canada. The value of the index of remoteness increases when moving from light colour shades to darker colours. Hence, as would be expected, the value of the index tends to increase as one moves away from major urbanized areas.
The lowest values of the index are recorded for the most urbanized regions of southern Ontario and southern Quebec. This reflects the fact that communities in these regions are in proximity to some of the largest metropolitan agglomerations of Canada, as well as a high concentration of medium and small size towns, which can facilitate access to a broad range of services, for social and economic development.
When looking at the frequency distribution pattern seen in Figure 1 and the inflection points of the distribution curve seen in Figure 2, some relevant insights can be made. First, there are no major break points in the distribution of the index values; that is, the curve is relatively smooth. Nevertheless, inflection points of the curve provide some insights on possible critical values of the index, which might be considered for use in the later transformation of the continuous index into representative categorical values.
The distribution curve increases in a concave manner downward until approximately an index value of 0.15 and shows a local plateau around that value (i.e. a concentration of CSDs around that value). Between a remoteness index value of 0 and that of 0.15 (inclusive) there are 773 CSDs, which correspond to 15% of CSDs for which the index is computed. The vast majority of them are located in southern Ontario and southern Quebec and southern British Colombia, within or in proximity to the major metropolitan areas of Canada.Note 20
Beyond the index value of 0.15, the curve presents a minor step with another portion increasing in a concave manner downward until an index value of approximately 0.40. There are 2,665 CSDs with remoteness index values between 0.16 and 0.40 (inclusive); that is, 51% of the CSDs fall into this value range. Beyond the index value of 0.40, the distribution curve presents an inflexion point and grows in a convex fashion until it reaches the upper bond of the index value at a value of 1.00. There are 1,772 CSDs with a remoteness index value between 0.41 and 1.00 (inclusive), which represents 34% of the CSDs for which a remoteness index value was computed.

Description for Figure 1
| Index value (range) | Number of CSDs |
|---|---|
| 0 to 0.05 | 15 |
| 0.05 to 0.1 | 171 |
| 0.1 to 0.15 | 559 |
| 0.15 -0.2 | 270 |
| 0.2 to 0.25 | 381 |
| 0.25 to 0.3 | 542 |
| 0.3 to 0.35 | 686 |
| 0.35 to 0.4 | 753 |
| 0.4 to 0.45 | 562 |
| 0.45 to 0.5 | 353 |
| 0.5 to 0.55 | 264 |
| 0.55 to 0.6 | 170 |
| 0.6 to 0.65 | 135 |
| 0.65 to 0.7 | 113 |
| 0.7 to 0.75 | 108 |
| 0.75 to 0.8 | 48 |
| 0.8 to 0.85 | 45 |
| 0.85 to 0.9 | 21 |
| 0.9 to 0.95 | 9 |
| 0.95 to 1 | 5 |
|
Source: Authors’ computations. |
|
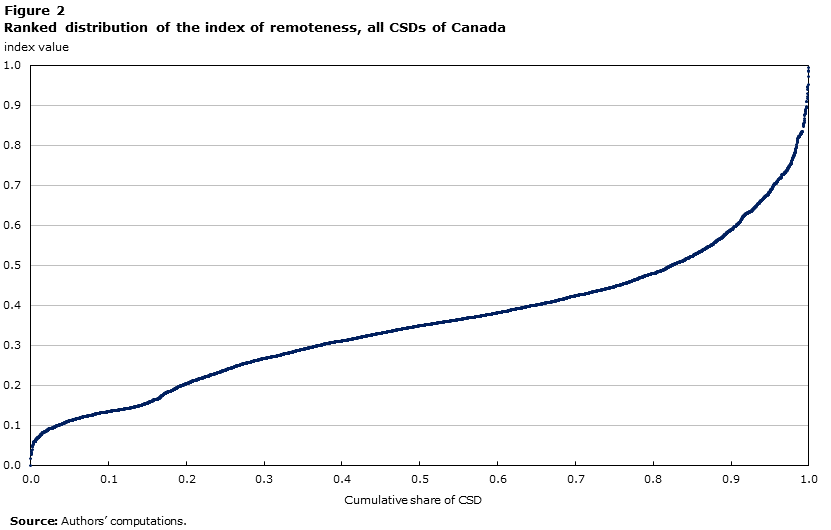
Description for Figure 2
Map 5 Spatial distribution of the index of remoteness, all CSDs of Canada

Description for Map 5
One of the most relevant questions for this index refers to its interpretability in relation to other prevailing standard geographic concepts. Addressing this question can also provide further insights into meaningful breakpoints of the continuous measure.
A cross tabulation of remoteness index statistics by Standard Area Classification (2011 census geography) is presented in Table 1. The Statistical Area Classification (SAC) groups census subdivisions into 8 classes, according to whether they are a component of a census metropolitan area, a census agglomeration or a census metropolitan influenced zone (MIZ).Note 21 This classification applies to all CSDs of Canada.
This table provides two relevant insights. The first is that, when looking at the average value of index by SAC class, there is a rather smooth upward progression of average values as one moves from CSDs which are within CMAs toward CSDs within the territories and which are outside of CAs. The only exception is the average for CSDs within CAs having no census tracts (0.32) which is higher (or more remote on average) than the average value for CSDs having strong metropolitan influence (0.24) and CSDs having moderate metropolitan influence (0.31). The second is that variability around these averages increases with a similar progression when moving from CSDs within CMAs to CSDs within the territories; the main exception, once again, is the values for CSDs within CAs having no census tracts.
| Type | Description | Mean | Standard deviation |
Min | Max | Range |
|---|---|---|---|---|---|---|
| 1 | Census subdivision within census metropolitan area | 0.17 | 0.08 | 0.00 | 0.35 | 0.35 |
| 2 | Census subdivision within census agglomeration with at least one census tract | 0.24 | 0.08 | 0.11 | 0.40 | 0.29 |
| 3 | Census subdivision within census agglomeration having no census tracts | 0.32 | 0.12 | 0.09 | 0.80 | 0.71 |
| 4 | Census subdivision outside of census metropolitan area or census agglomeration area having strong metropolitan influence | 0.24 | 0.11 | 0.08 | 0.57 | 0.49 |
| 5 | Census subdivision outside of census metropolitan area or census agglomeration area having moderate metropolitan influence | 0.31 | 0.13 | 0.08 | 0.83 | 0.75 |
| 6 | Census subdivision outside of census metropolitan area or census agglomeration area having weak metropolitan influence | 0.43 | 0.14 | 0.13 | 0.95 | 0.82 |
| 7 | Census subdivision outside of census metropolitan area or census agglomeration area having no metropolitan influence | 0.48 | 0.16 | 0.09 | 1.00 | 0.91 |
| 8 | Census subdivision within the territories, outside of census agglomeration | 0.71 | 0.14 | 0.47 | 0.99 | 0.52 |
| All Census subdivision | 0.36 | 0.17 | 0.00 | 1.00 | 1.00 | |
| Source: authors’ computation. | ||||||
The relationship between remoteness index values and SAC types is further evidenced by the scatter plots of Figure 3 and Figure 4. Each panel of these figures shows the distribution of the index values for each of the eight SAC classes. All CSDs that belong to a CMA have an index value equal to or lower than 0.35. In addition, all of the CAs that contain census tractsNote 22 have an index value equal to or less than 0.4. Hence, this boundary value of the index (0.4) would capture all of the CSDs within the boundary of CMAs or CAs with a core population of 50,000 or more.
CSDs within smaller CAs (which have not been divided into census tracts due to having a core population of less than 50,000) present much more diverse conditions in terms of remoteness.Note 23 Within this group there are communities with index values ranging from 0.1 to 0.8, that is, from the lowest to the highest level of remoteness. Some of these small-size agglomerations are regional service centres in relatively remote and isolated areas, which tend to report relatively high remoteness index values (above 0.4). Examples are CSDs found within the CA of Prince Rupert, BC (CSD index value of 0.42 and 0.44), the CA of Corner Brook, Newfoundland and Labrador (CSD index values ranging from 0.38 to 0.46), and the CA of Thompson, Manitoba (index value of 0.43 for both CSDs belonging to this CA).
Other CAs falling within this category (i.e. having no census tracts) are small-size agglomerations in densely populated regions or located in relative proximity to other major agglomerations and therefore have lower values on the index of remoteness. Examples are Woodstock, Ontario (index value of 0.09), Camrose, Alberta (index value of 0.21), and New Glasgow, Nova Scotia (index values ranging from 0.29 to 0.31).
Finally, there are CAs that show substantial diversity among their component CSDs. For instance, the CA of Quesnel, British Columbia, reports index values for its CSDs which range from 0.38 to 0.80; CSDs within the CA of Wood Buffalo, Alberta, report index values ranging from 0.32 to 0.74. These are examples of CAs composed of communities with remarkably different remoteness values.
The Metropolitan Influenced Zone (MIZ) types (strong, moderate, weak and no influence) also demonstrate substantial variation amongst index values. This result is particularly revealing and sheds further light on the different dimensions captured by the SAC typology and the remoteness index. This diversity of conditions is particularly marked for CSDs which belong to the moderate to no-influence types; there are 2,004 CSDs classified as moderate, weak or no-influence that report a value of the index which is comparable to CSDs within the boundary of a CMA or CA (that is, less than or equal to 0.4).
More interestingly, there are 779 CSDs belonging to a MIZ type (strong, moderate, weak or no-influence) that have remoteness values comparable to those typical of the CSDs in the territories (outside of CAs). In fact, with the exception of 3 CSDs, all CSDs in the territories (outside of CAs) report a value of the remoteness index greater than 0.5.
Two main points emerge from these results. The first is related to the dimension which is captured by the index of remoteness; the second is related to possible critical values that could be considered in the categorization of CSD into categorical classes of remoteness.
The index of remoteness captures a unique and distinct geographic dimension of the CSD, which, as one would expect, has a degree of overlap with the SAC, but at the same time puts the emphasis on the geographic location as opposed to observed socio-economic ties measured by commuting flows. The SAC typology captures the presence or absence of commuting linkages; conversely, the remoteness index captures the proximity dimension, regardless of actual commuting flows between communities. Moreover, the MIZ classification captures only the influence of major metropolitan areas, that is, for the MIZ classification the commuting flows are measured only with respect to CMAs and CAs. By contrast, the value of the index of remoteness is also affected by smaller population centres ( outside CMAs or CAs), which might play a significant role as regional service centres in less populated regions.
With respect to possible critical values, it appears that the values of approximately 0.2, 0.4, and 0.6 would capture meaningful turning points along the 0 to 1 range. Most CSDs in proximity to major agglomerations are found below or in the vicinity of the 0.15 value (Figure 1), hence a cut-off value of 0.2 would include this group. The highest frequency of values are in the range 0.2 to 0.4, which would include all the CSDs belonging to a CAs with over 50,000 inhabitants (having at least one census tract); this range appears to provide a representation of CSDs with a certain degree of proximity to medium size agglomeration. Beyond this point there is a group of CSDs with some moderate degree of remoteness; finally, CSDs with index values greater than 0.6 have a condition of relative geographic isolation that is typical of the territories, indeed this range includes all CSDs within the territories, plus 431 CSDs located in other provinces that experience a comparable degree of physical isolation from population centres.

Description for Figure 3a
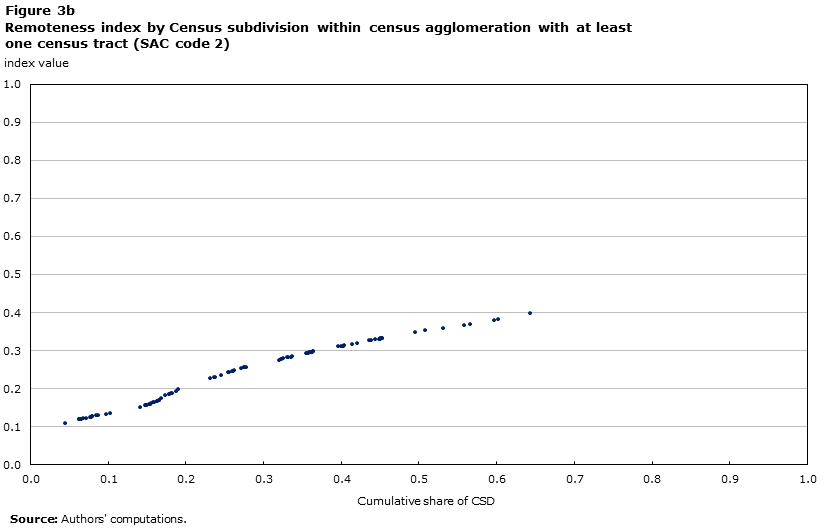
Description for Figure 3b
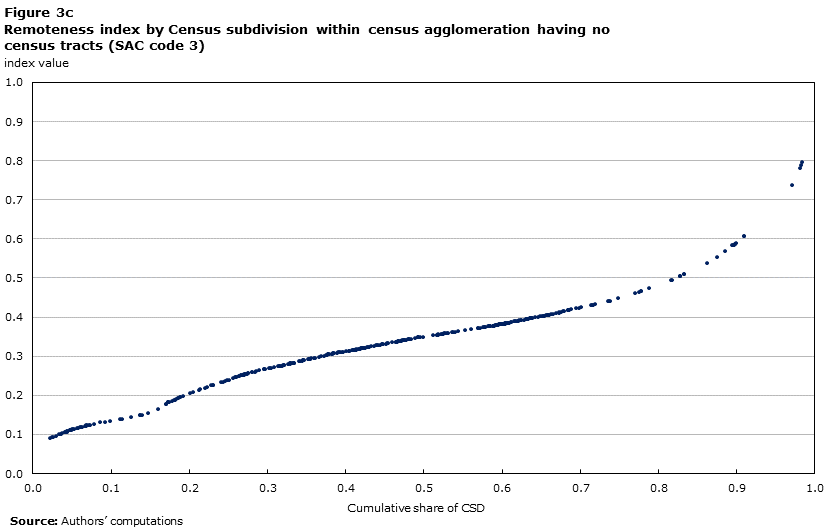
Description for Figure 3c
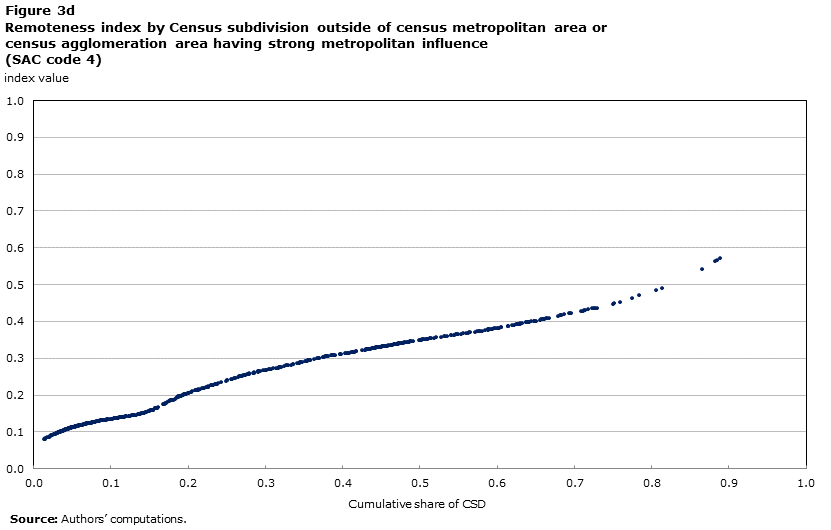
Description for Figure 3d

Description for Figure 4a

Description for Figure 4b
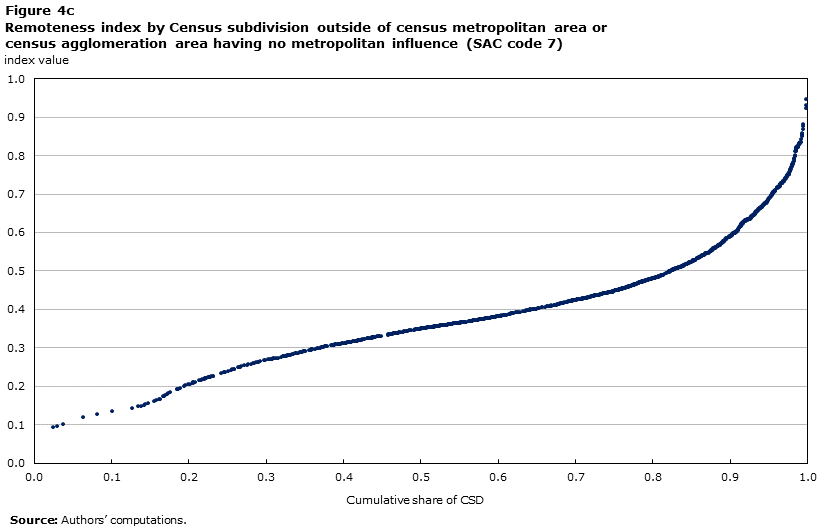
Description for Figure 4c
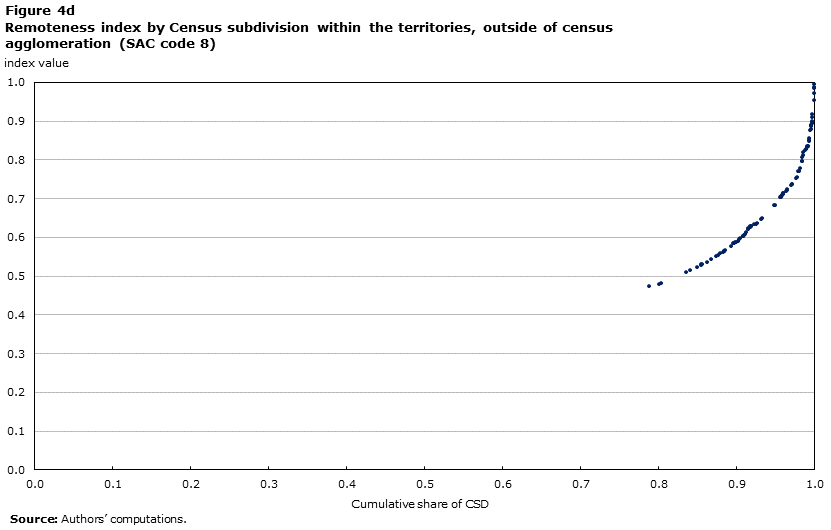
Description for Figure 4d
Accessibility measures
Accessibility measures for selected services were generated as a by-product of the primary analysis of the remoteness index. A set of these measures are presented here to illustrate the potential of the methodological approach. Several refinements and variations of these measures could be computed with a focus on selected services or selected units of measures of accessibility. In the examples that are outlined here, the existence of service providers was identified by geocoding information, extracted from the Business Register for selected NAICS codes.
Since the computations presented here are done using the value of the service available in the CSD, most CSDs, including both those connected to a population centre through the road network and those not so connected, yield an accessibility measure. This is especially true for services that are commonly available such as retail services. However, for the few CSDs which were not connected to a population centre through the road network and without the given service available locally, the accessibility measures were not computed. These communities are flagged as communities in which the service is not directly accessible (labelled as “no direct access”).
Overall, the most striking result is the relationship between accessibility measures and the index of remoteness. Generally, the index of remoteness is highly correlated with the accessibility measures, which provides support to the hypothesis that population size can be used as a reliable proxy for provision of services. Thus, an index of remoteness could also be used to provide a relatively good approximation of the availability of services to the community. These results are in line with the available literature, which suggests that the population size of an agglomeration is the best proxy for the availability and variety of general services (business, health, education, etc).
The correlations between the index of remoteness and each the accessibility measures are presented in Table 2. In general, the correlation between the remoteness index and the accessibility measure is high (between 0.74 and 0.93, in absolute value terms); therefore, the remoteness index provides a reasonable approximation for the measurement of accessibility to each selected service. In addition, the measures of accessibility generally present an even higher correlation among themselves (in all cases, the correlation is higher than 0.76).
| Remoteness | All health services (62) | Ambulatory Health Care Services (621) | Hospitals (622) | Nursing and Residential Care (623) | Social Assistance (624) | Credit intermediation (522) | Legal services (5411) | Selected retail services | |
|---|---|---|---|---|---|---|---|---|---|
| Correlation coefficient in absolute value terms | |||||||||
| Remoteness | 1.00 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| All health services (62) | 0.93 | 1.00 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Ambulatory Health Care Services (621) | 0.85 | 0.88 | 1.00 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Hospitals (622) | 0.74 | 0.76 | 0.77 | 1.00 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Nursing and Residential Care (623) | 0.84 | 0.87 | 0.92 | 0.82 | 1.00 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Social Assistance (624) | 0.84 | 0.88 | 0.93 | 0.78 | 0.90 | 1.00 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Credit intermediation (522) | 0.85 | 0.86 | 0.94 | 0.78 | 0.90 | 0.91 | 1.00 | Note ...: not applicable | Note ...: not applicable |
| Legal services (5411) | 0.83 | 0.85 | 0.93 | 0.73 | 0.91 | 0.91 | 0.91 | 1.00 | Note ...: not applicable |
| Selected retail services | 0.87 | 0.86 | 0.94 | 0.77 | 0.91 | 0.90 | 0.91 | 0.91 | 1.00 |
|
... not applicable Note: Numbers in brackets in column and row headings are corresponding NAICS codes. Retail service is a selection of NAICS 44 and 45 codes. All coefficient values are in absolute value terms. CSD with “no direct access” to the service are not included in the computation of the correlation coefficients. Source: authors’ computations. |
|||||||||
This overall pattern does not preclude the accessibility measures from providing valuable information, in addition to that provided by the remoteness index. On the contrary, accessibility conditions to selected services, particularly in the most remote areas, would still provide valuable information for specific operational purposes. Also, separate accessibility measures may still be used to enrich a remoteness index purely based on proximity and population size. Nevertheless, for broader purposes, Table 2 supports the view that the method outlined here to measure remoteness provides a relatively transparent and straightforward approach to represent the condition of a community in terms of its accessibility to various types of services.
The following sections present in greater detail the accessibility measures for health services, selected retail services, banking and legal services. A database with community values generated at the CSD level is available from the authors upon request. It should be noted that, in order to align the values of the remoteness index and accessibility measures, the complement to 1 of the accessibility measure is presented. Thus, a low value of the accessibility measure indicates a high availability of services, just as a low value of the remoteness index indicates a low remoteness.
Health services
For the purpose of this analysis, health services in a CSD are identified by businesses associated with the NAICS code 62. This includes all the three digit codes associated with the Health Care and Social Assistance sector: Ambulatory Health Care Services (621), Hospitals (622), Nursing and Residential Care Facilities (623), and Social Assistance (624). To provide a better understanding of the potential and limitations of accessibility measures for selected services, the results of the accessibility measures are plotted for health services as a whole (NAICS 62), and then for the four subgroups (three digit NAICS).
Figure 5 shows the value of the accessibility measure to health services (NAICS 62) plotted against the ranked distribution of the remoteness index. Once again, a remoteness index of 0 indicates low remoteness, while a low value of the accessibility measure means high accessibility of health services. The most striking feature of this figure is the concentration of communities within a narrow range of this accessibility measure, representing relatively high access to this type of services. Of the 5,062 CSDs for which the measure is calculated, 4,243 have accessibility measures within the range of 0.1 to 0.3; that is, the large majority of CSDs across Canada enjoy a similarly high level of physical accessibility to health services. However, 490 communities fall into an area of relatively lower level of accessibility, with values higher than 0.3 in Figure 5. In addition, 109 CSDs have no value for this accessibility measure (i.e., no direct access to this service); of these 37 contain no population.
Figure 6 shows the distribution of the accessibility measure for the four types of health services (three digit NAICS classification), compared to the ranked distribution of the index of remoteness. Hospital services (622) have the lowest correlation coefficient with the remoteness index (0.74, in absolute value terms) (Table 2).Note 24 The very large majority of CSDs have access to hospitals, with very few CSDs having low or no access to hospitals. One hundred and forty-four CSDs have no value, of these 44 contain no population and the remaining ones both are not connected to a population centre through the road network and also have no businesses within the CSD for which revenues are reported in the Business Register under NAICS code 622.Note 25

Description for Figure 5
The accessibility measure to health services is mapped in Map 6. The pink circles indicate non-connected CSDs in which no health services are reported in the BR. In general, remote communities with health services available locally have a low value of accessibility because the revenues reported are low.
Map 6 Geographic distribution of the accessibility measure to health services (NAICS code 62)

Description for Map 6
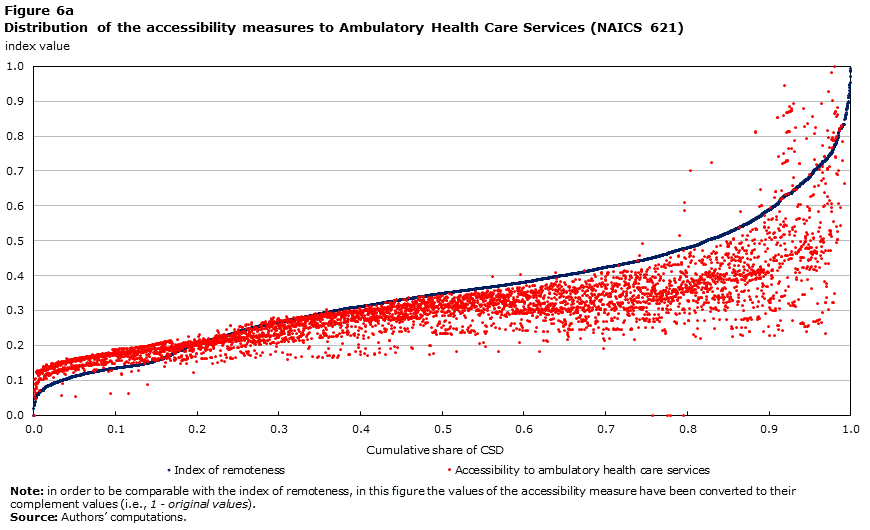
Description for Figure 6a
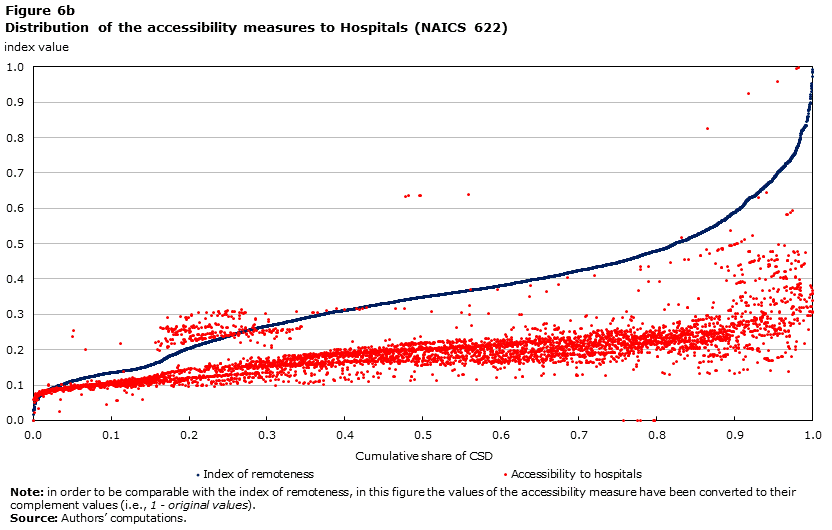
Description for Figure 6b
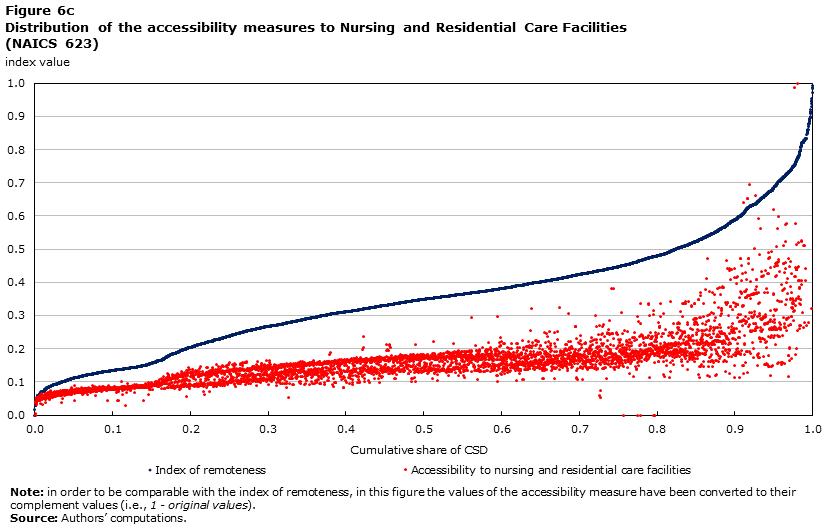
Description for Figure 6c

Description for Figure 6d
Selected retail services
The focus of the analysis is on retail activities that are more directly related to production activities, supporting business activities, or retail stores that may be particularly relevant within the economic and retail context of small communities (such as general merchandise stores). Hence, only 5 of the 12 four digit NAICS codes classified as retail are included in this aggregate; these are: Motor vehicle and parts dealers (441); Electronics and appliance stores (443); Building material and garden equipment and supplies dealers (444); Gasoline stations (447); and General merchandise stores (452).Note 26 Figure 7 shows the distribution of the accessibility measure for retail services. Retail services have the highest correlation coefficient with the remoteness index (0.87, in absolute value terms) (Table 2).
The value of the accessibility measure for the selected group of retail services are plotted against the ranked distribution of the remoteness index in Figure 7. This figure further illustrates the high correlation between the two measures, suggesting that some accessibility to this basic service is generally available across communities and, as one would expect, is proportional to measures of population size and access to agglomeration. Of the 134 communities that do not have a value for this measure, 38 have no population and all remaining CSDs are not connected to a population centre through the road network.

Description for Figure 7
Map 7 shows the spatial distribution of the accessibility measure to the selected group of retail services. As with earlier findings, the map points to the fact that community with lower level of access (dark shades) or no direct access are generally located in the most peripheral areas of the county.
Map 7 Geographic distribution of the accessibility measure to selected retail services (NAICS 441, 443, 444, 447, and 452)
Description for Map 7
Financial and legal services
For the purpose of this analysis, financial services are identified by the NAICS code 522 - Credit intermediation and related activities. As described by the NAICS definition, “this subsector [NAICS 522] comprises establishments primarily engaged in lending funds raised from depositors or by issuing debt securities and establishments that facilitate the lending of funds or issuance of credit by engaging in such activities as mortgage and loan brokerage, clearinghouse and reserve services, and cheque-cashing services.” Note 27 Legal services are identified in the NAICS by the code 5411 - Legal services. This industry group comprises establishments primarily engaged in providing legal and paralegal services; establishments in this industry group are offices of lawyers (NAICS 54111), offices of notaries (54112) and Other legal services (NAICS 54119), such as offices of paralegals.
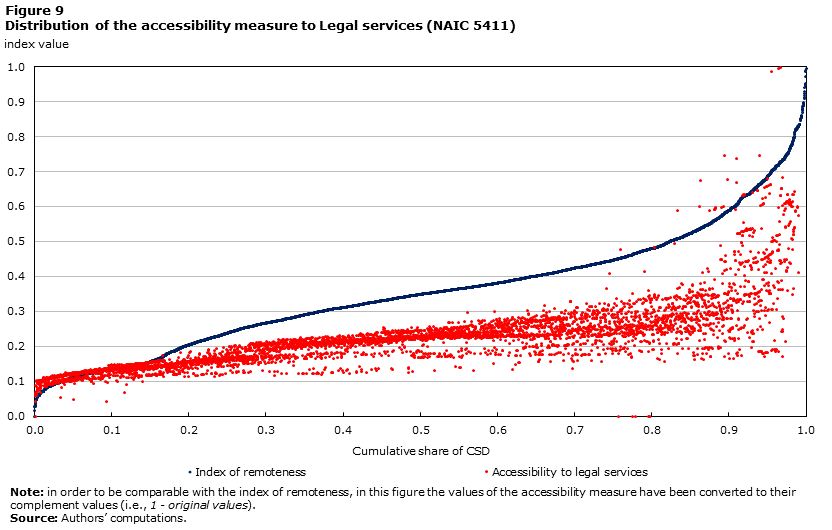
The value of accessibility measures for financial and legal services are plotted against the ranked distribution of the remoteness index in Figure 8 and Figure 9, respectively. Once again, the values used for these figures are the complement to one of the original values, thus a value of 0 indicates the most access and a value of 1 indicates the least access to these services.
Two points are worth emphasizing; the first is that CSDs with no direct access to these services start to appear when the index of remoteness reaches the range of 0.4 to 0.5, suggesting once again that this is a critical value of transition in terms of proximity to centres capable of supporting a variety of services. The second is that for each range of the remoteness index the dispersion of accessibility measures appears generally greater for banking services than for legal services. This might reflect different distribution patterns for point of services provision as well as different or emerging opportunities for the delivery of some of these services (such as online banking).

Description for Figure 8
Description for Figure 9
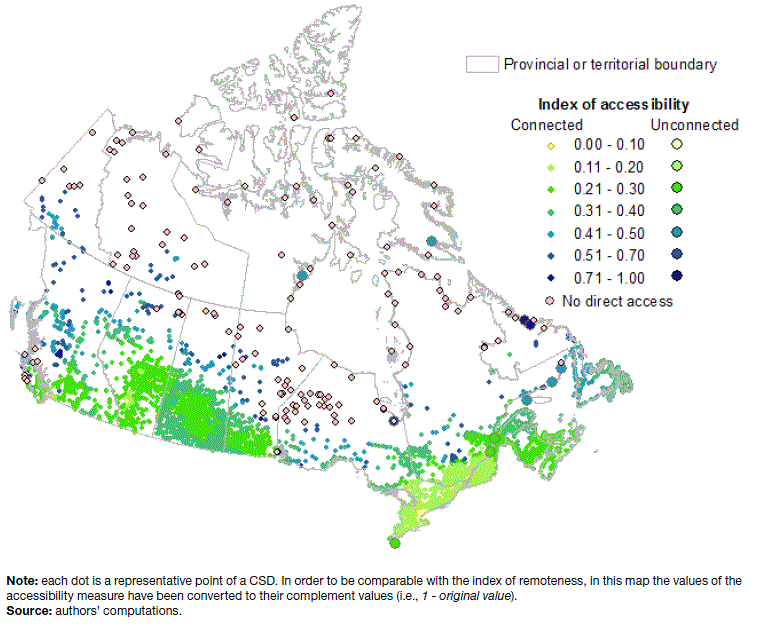
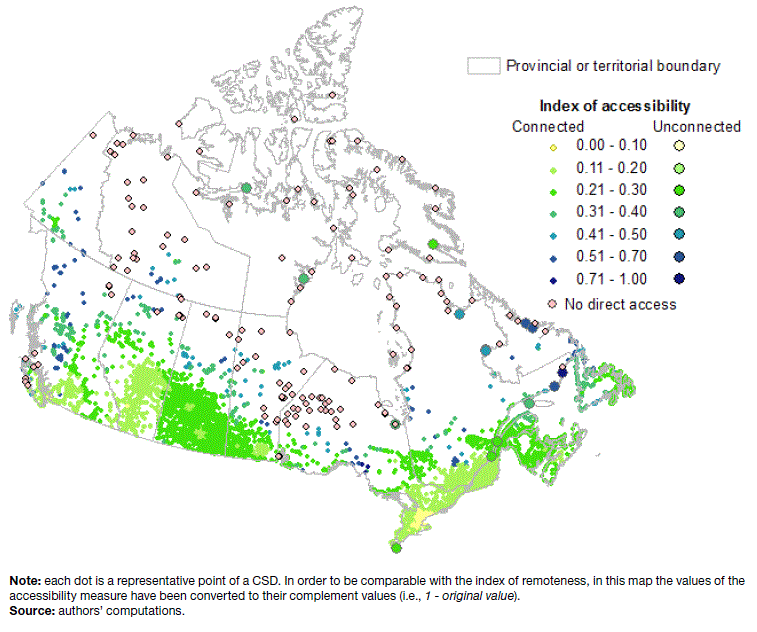
The following two maps show the spatial distribution of the accessibility measure to credit intermediation and related activities (Map 8) and to legal services (Map 9). The maps point to the fact that communities with lower level of access (dark shades) or no direct access are generally located in the most peripheral areas of the country.
Map 8 Geographic distribution of the accessibility measure to Credit intermediation and related activities (NAIC 522)
Description for Map 8
Map 9 Geographic distribution of the accessibility measure to Legal services (NAIC 5411)
Description for Map 9
Conclusions and potential developments
This paper presented a methodology and results for an index of remoteness, complemented by a set of accessibility measures to selected services. The index was computed for all CSDs of Canada that recorded some population in 2011 or that were connected to the road network. The database with the index and accessibility measures is released as an experimental database for testing and analysis and is available from the authors upon request.
The methods that were used in this analysis build on the insights generated through a review of the applied literature on the subject of remoteness and accessibility, as well as on discussions with and insights from potential users of the indices, and extensive empirical testing of alternative specification methods. This background work helped establish the guiding principles and required characteristics of the index, which included relative simplicity, parsimonious use of input data, and ease of future maintenance.
The index of remoteness generated in this analysis is a continuous measure, which can be converted into any categorical classification of remoteness. The approach that was used addresses some specific challenges, like the need to account for multiple point of access to services; it also establishes a continuum between communities with different transportation infrastructures and connectivity while at the same time retaining the information on the community transportation infrastructures in the database.
Some relevant findings and broad considerations should be emphasized. First, the results show that an index of remoteness based on distance to multiple population centres provides a reasonable approximation of overall physical accessibility to services, shown by the fact that the remoteness index and accessibility measures are, in general, highly correlated. The general model could be further refined to derive more specific indicators of accessibility to services for research and policy analysis applications. Nevertheless, the information generated by specific accessibility measures, particularly for the most remote areas, would still provide valuable information for particular operational purposes and may result in separate accessibility measures that could be used to enrich a remoteness index based on proximity and population size alone.
Second, the analysis shows that the index of remoteness captures a unique geographic dimension, distinct from what is captured by other predominant geographic classifications such as the Standard Area Classification (SAC). The information provided by the index relates to the potential interactions due to proximity, as opposed to observed linkages such as commuting.
Third, in spite of some computational challenges due to the relatively large size of the datasets, the methods used to create the index are conceptually straightforward and transparent, and the computation also makes parsimonious use of input data. More importantly, the input data are maintained in a manageable number of input databases and can be easily updated if specific circumstances change for a community; for instance, due to local changes to the transportation infrastructures, on in population counts.
This type of analysis, which involves detailed geocoding, also has potential applications for use in quality control of official statistical products. For instance, by comparing the index of remoteness, which is population based, with the accessibility measures generated from the Business Register data, it is possible to highlight spatial patterns of the index values that warrant further investigation. This analysis might help with identifying areas of possible improvement for the official statistical sources, or provide insights for the interpretation of aggregate trends for specific indicators.
More broadly, this analysis illustrates the potential benefits of combining data from official statistical sources (in this case, Census and Business Register microdata) with data that are generated from non-official statistical sources (in this case, mainly distance measures generated from the Google Maps API). The databases used as input data in the computation could be further refined and updated as non-official statistics are further explored and integrated into statistical programs ; for instance, expanding the use of transportation costs collected online through web-scraping in order to refine some of the transport cost parameters between specific representative points.
Finally, it should be emphasized that the methods and results of this analysis can be further developed in several directions. This is particularly true for the set of accessibility measures, which at this stage have been developed as a by-product of the main index of remoteness. Although the methodology outlined here is complete and fully specified, it is offered only as a proposed option which can be further refined and developed. As such, the results presented in this paper can constitute the foundation for further dialogue with a broad set of stakeholders within various departments and agencies that are currently making use of remoteness and accessibility measures for policy development and program delivery.
References
Australian Institute of Health and Welfare - AIHW (2004). Rural, regional and remote health: A guide to remoteness classifications. Rural Health Series No. 4. AIHW Catalogue Number PHE 53. Canberra.
Battersby, Bryn, and Robert Ewing (2005). "International Trade Performance: The Gravity of Australia's Remoteness." Treasury Working Paper No. 2005-03. Australian Treasury, Canberra.
Bhat, Chandra, Susan Handy, Kara Kockelman, Hani Mahmassani, Lisa Weston, Anand Gopal, and Issam Srour (2002). Development of an Urban Accessibility Index. Project 0-4938: Project Summary Report 4938–S. Center for transportation research. The University of Texas at Austin.
Department of Health and Ageing - DHA (2009). Bonded Medical Places Scheme: Information booklet for 2009. Australian Government. Online Page last modified: December, 2009.
Department of Health and Ageing - DHA (2005). Review of the Rural, Remote, and Metropolitan Areas (RRMA) Classification. Discussion Paper (Without Prejudice). Australian Government, DoHA. Canberra.
Duran Fernandez, Roberto (2008). Gravity, Distance, and Traffic Flows in Mexico. Transport Studies Unit. Working paper N° 1030. Oxford University Centre for the Environment.
Evans, Lewis, and Patrick Hughes (2003). Competition Policy in Small Distant Open Economies: Some Lessons from the Economics Literature. Working Paper 03/31, New Zealand Treasury.
Frankel, Jeffrey A., and David Romer (1999). "Does Trade Cause Growth?" The American Economic Review. 89 (3):379-399.
Girma, Sourafel, and Zhihao Yu (2002). The Link between Immigration and Trade: Evidence From the U. K. Review of World Economics, 138 (1):115-130.
Luo, W., and, F. Wang (2003). Measures of spatial accessibility to health care in a GIS environment: synthesis and a case study in the Chicago region. Environment and Planning B: Planning and Design 30, 865–884.
Luo, Wei and, Yi Qi (2009). An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health and Place (December 2009), 15 (4):1100-1107.
McGrail, Matthew R., and John S. Humphreys (2009). Measuring spatial accessibility to primary care in rural areas: Improving the effectiveness of the two-step floating catchment area method. Applied Geography (December 2009), 29 (4):533-541.
OECD (2012). Measuring the access to public services: the case of public hospitals. Paper presented at the OECD Working Party on Territorial Indicators, Paris 3 December 2012.
OECD (2014). Accessibility to services and regional well-being: a framework to build indicators. Paper presented at the OECD Working Party on Territorial Indicators, Paris 9-10 April 2014.
Pooler, James A. (1995). The use of spatial separation in the measurement of transportation accessibility. Transportation Research Part A: Policy and Practice. 29 (6):421-427.
Simon, Howard, Arnold Reisman, Shahriar Javad, and Diane Sachs (1979). An Index of Accessibility for Ambulatory Health Services. Medical Care, Vol. 17 (9):894-901.
Stifel, David, Bart Minten, and Paul Dorosh (2003). Transactions costs and agricultural productivity: implications of isolation for rural poverty in Madagascar. MSSD Discussion Paper No. 56. International Food Policy Research Institute.
Wakerman, John, and John Humphreys (2008). Rural and remote health — definitions, policy and priorities. In Siaw-Teng Liaw and Sue Kilpatrick, Editors), A Textbook of Australian Rural Health. Australian Rural Health Education Network. Canberra, ACT.
Wu, JunJie, and Munisamy Gopinath (2008). What causes spatial variations in economic development in the United States? American Journal of Agricultural Economics, 90 (2):392-408.
- Date modified:

