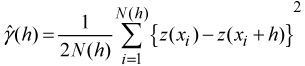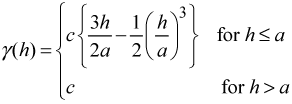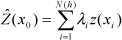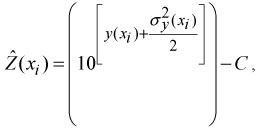Main article
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
1 Introduction
This study describes the methodology developed to calculate the water yield for Canada. The purpose of developing this methodology is to fill a data gap in Statistics Canada's Water Accounts, namely the freshwater asset account (Soulard, 2003). This gap stems from the fact that estimates of freshwater flow for Canada have not been calculated regularly and have been produced using methods that do not generate comparable results (Sanderson and Phillips, 1967; Laycock, 1985; Pearse et al., 1985). This represents an analytical barrier since the proper study of water availability, especially from a supply and demand perspective, requires spatial and temporal comparability of data. The methodology developed here results in a thirty-year (1971 to 2000) annual average of water yield for Canada that is coherent through space and time, and that will allow us to study the availability and renewal of water resources on a more disaggregated basis.
Specifically, the objectives of the study were to:
- create surfaces of annual runoff through spatial interpolation; and
- quantify spatial estimates of annual water yield for Canada using the runoff surfaces.
This paper will discuss in detail the methodology (Section 2) and the results (Section 3).
1.1 The water yield
The water yield is defined in this paper as the amount of freshwater derived from unregulated flow (m3 s-1) measurements for a given geographic area over a defined period of time. The freshwater flow is generated from a combination of baseflow, interflow and overland flow originating from groundwater, precipitation and/or snowpack. The flow rate encompasses the hydrologic processes (for example, interception, infiltration and evapotranspiration), the state of water storage (for example, lakes, aquifers, snowpack and soil moisture) within a drainage basin (Mosley and McKerchar, 1993) and is influenced by climatic (for example, temperature) and physiographic (for example, topography) variables. The water yield is based on unregulated flow in that only measurements exhibiting natural flow (that is, not dammed or diverted) are used in its computation. Flow is exclusively used to estimate water yield because it can be measured with a known level of accuracy (Dingman, 1994) compared to other parts of the water cycle such as precipitation and evapotranspiration, which can contain higher levels of uncertainty.
1.2 The water accounts
The water yield methodology was developed to provide estimates of stocks of water assets for the Water Accounts component of Statistics Canada's environmental accounting framework, the Canadian System of Environmental and Resource Accounts (CSERA). 1 The Water Accounts offer an integrated view of water and its use by society; this integrated view is based on a compilation of environmental data that is consistent over space and time, national in coverage and compatible with economic accounts supporting our ability to understand and address water issues in Canada. The system was created to respond to the need for better monitoring of the relationships between human activity and the environment.
2 Data and methods
To produce a thirty-year estimate of annual average water yield for Canada there were four main processing steps. The first step involves the development of a data framework for Canada that can be used for estimating annual water yield. The second step consists of the calculation of the runoff per unit surface area using the data framework. The third step uses the runoff values to generate a spatial distribution of monthly runoff over the extent of Canada for each of the thirty years. Finally, in the fourth step, the monthly runoff surfaces are scaled to produce water yield estimates that are, in this study, averaged to generate a thirty-year national estimate. The subsequent sections provide a detailed explanation of each of these processing steps.
2.1 Building the data framework
Different datasets and processing efforts were required to develop a national data framework for Canada from 1971 to 2000. The following sections provide a description of the datasets along with the processing steps used in building the framework. In brief the main steps to build the framework are:
- assembly of streamflow gauging stations across Canada that exhibit natural flow;
- compilation of contributing basin areas for each station; and
- relocation of stations to the centroid of their contributing areas.
2.1.1 Streamflow
The first step in building the data framework involves assembling the hydrometric data. The monthly streamflow (m3 s-1) data used were from the HYDAT (HYDEX) 2005 database (Environment Canada, 2007). 2 This 2005 database contains streamflow data for over 2100 active stations and close to 4200 discontinued stations across Canada. Each station in the database is accompanied by fields containing their unique identifier, latitude/longitude, drainage area (km2), period of operation, regulation flag, and remarks containing such information as data quality and type of regulation.
The HYDAT database was filtered to include only stations with natural flow using the HYDEX field indicating regulation. Subsequent to all filtering, the remarks fields for each station were evaluated: if the remarks indicated there were regulating characteristics within a basin, the station was removed from the database. However, regulated stations were retained when the remark indicated the regulation had an insignificant impact on the streamflow. In addition, exceptions were made to stations in the Arctic where remarks contained cautionary details because there were only a few stations available. There were a number of stations where recordings ceased during the winter months. These stations were assigned a value of zero for the non-reporting months if the last day of the month preceding and the first day following the break in recording contained zero values. Chart 1 displays the average, minimum and maximum number of stations included each year after filtering the HYDAT database for the duration of the study period.
2.1.2 Contributing basins
The second step in building the data framework entailed the identification of the drainage area for each station. These drainage areas, or contributing basins, were compiled from three main sources:
- the Prairie Farm Rehabilitation Administration (PFRA) drainage basins (PFRA, 2004);
- the National Scale Drainage Framework (NSDF) ver.5 (Natural Resources, 2003); and
- the HYDEX database (Environment Canada, 2003).
All spatial data were projected to an Albers Equal Area Conic projection. 3 The HYDEX areas were compared to the PFRA and NSDF; when problems or significant discrepancies were noted, a visual assessment was conducted of the spatial coverage.
The PFRA database covers all of Alberta, Saskatchewan and Manitoba, and portions of adjacent jurisdictions into which Prairie watersheds extend (PFRA, 2004). For the area of the country that falls under the mandate of the PFRA, the contributing basin data produced and maintained by the PFRA were used. This dataset provides the effective and gross contributing basin areas. The effective drainage is defined as the portion of a drainage basin which is expected to contribute runoff to the main stream during a flood with a return period of two years. The gross drainage is described as the plane area enclosed by its watershed, which might be expected to contribute runoff to that specified location under extremely wet conditions (Godwin and Martin, 1975). The effective drainage areas were considered to be most suitable for this study. Incorporating this dataset into the framework necessitated considerable processing, primarily to remove non-HYDAT stations and to either remove or merge their contributing areas. There were also multiple locations in the PFRA database for some stations that were moved over time, therefore only the most recent locations were retained.
The NSDF includes polygons defining the contributing basins for all HYDAT stations draining an area greater than 200 km2. For all areas of Canada falling outside of the PFRA, the NSDF was used. An initial comparison of the areas of the contributing basins as reported in the NSDF with the areas published in HYDEX showed that many of the basins generated for the NSDF were not well defined. A visual assessment of the NSDF polygons revealed that there were many basins that either had "holes" in their coverage or appeared to be defined larger than they should be because of the scale of the stream network used to define them. When comparing the NSDF to HYDEX basin areas, it was found that when the NSDF areas were smaller than the HYDEX areas it was frequently a result of the "holes" found in the coverage. These "holes" may have resulted from lakes that were not connected to the stream network and as a result were not considered in the technique used to delineate the basin areas. When the NSDF basin areas were larger it was likely because the generalized stream network used to generate the contributing basin boundaries was not detailed enough to constrain the boundaries to their proper location. As a result the contributing basin areas published in HYDEX were used instead of the NSDF for calculating the runoff per unit surface area values in Section 2.2.
A detailed description of how the PFRA, NSDF and HYDEX basins were generated is beyond the scope of this paper, a complete description of the methodology can be found in PFRA, (2004), Brooks et al, (2002), and Environment Canada, (2007), respectively.
2.1.3 Centroid positioning
The third step in building the data framework consists of finding the location to which to assign the unit runoff value. Each HYDAT station was relocated to the centroid of each of their corresponding contributing areas. This was done because runoff values positioned at the centroid of their contributing basins are more representative of the basin than the gauge location when estimating runoff per unit surface area (Krug et al., 1990). The contributing area was considered to be any area upstream from the station even if it overlapped other upstream stations.
The NSDF basins were used for centroid positioning in areas where PFRA coverage was not available. While not used as the source of the area values used to derive runoff, in a majority of cases the general shape and alignment of the NSDF drainage area polygons were deemed appropriate for the task of locating the centroid. Since the NSDF dataset did not contain basins smaller than 200 km2 and there were many HYDAT stations that fit this criterion, they were inserted into the dataset without being repositioned to the centroid of their contributing areas. This is considered to have no impact on the final estimate since the shift in position would be minimal. The final data framework of monthly streamflow centroids, by data source is presented in Map 1.
2.2 Runoff per unit surface area
Once the data framework was built, the next step of the model involved
the calculation of a runoff per unit surface area (mm) (that is, runoff depth).
This was completed by dividing the monthly streamflow values by their contributing
area and attributing the results to the centroids. This was only done for
basins with areas smaller than 5000 km2. This condition
assumes that the hydrological response is more likely to be related to the
streamflow measured at a station for basins with areas
 5000 km2. The existing
literature provides sufficient evidence that this is an acceptable criterion,
despite its potential limitations.
5000 km2. The existing
literature provides sufficient evidence that this is an acceptable criterion,
despite its potential limitations.
The
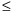 5000 km2 threshold is based on the
Annual Unit Runoff of the Canadian Prairies study conducted by Bell, (1994)
which assumed that larger contributing basins would contain a more diverse
mixture of hydrologic conditions. Although this condition was established
for basins found in the Prairies, and in all likelihood basin size may not
indicate more complexity for other regions of the country, it is considered
to be a reasonable assumption to limit the size of area for determining the
unit runoff. Krug et al, (1990) uses a similar condition for mapping
mean annual runoff in selected areas of the United States. As a result, contributing
basin areas in this study range from 0.16 km2 to 4950 km2 with a median size of 278 km2 (Chart 2).
5000 km2 threshold is based on the
Annual Unit Runoff of the Canadian Prairies study conducted by Bell, (1994)
which assumed that larger contributing basins would contain a more diverse
mixture of hydrologic conditions. Although this condition was established
for basins found in the Prairies, and in all likelihood basin size may not
indicate more complexity for other regions of the country, it is considered
to be a reasonable assumption to limit the size of area for determining the
unit runoff. Krug et al, (1990) uses a similar condition for mapping
mean annual runoff in selected areas of the United States. As a result, contributing
basin areas in this study range from 0.16 km2 to 4950 km2 with a median size of 278 km2 (Chart 2).
2.3 Runoff interpolation
Numerous studies have been conducted to compare the performance of interpolation techniques for producing spatial estimates. The studies that were reviewed for this paper (Tabios and Salas, 1985; Abtew et al., 1993; Borga and Vizzaccaro, 1997; and Syed et al., 2003) focus on the interpolation of precipitation from rainfall gauges, but the methodology is considered to be similar to what would be used for the interpolation of runoff. The general consensus of these studies is that kriging provides the optimum surface prediction. To ensure kriging was suitable for the data used in this study, a comparative analysis was conducted between kriging and radial basis function interpolators (for example, multi-quadric, thin-plate spline and spline with tension). Kriging produced the best results in areas where values over short distances were highly variable and where the density of points either decreased or were not present near the border of the study area. Kriging also provided a smoother surface that captured the local variation without including "bull's-eye" 4 effects, which were produced when using the radial basis function interpolators. In addition, it was advantageous to use kriging over other interpolators because it was possible to produce a standard error of the prediction, which defined uncertainly levels of the interpolated surface. Eaton et al., (2002) as well as Krakauer and Fung, (2008) are examples of studies that have used kriging for the interpolation of runoff at the regional and national level.
As with other interpolation methods, kriging uses the values of nearby observations to estimate the values at unmeasured locations. The kriging estimator is a weighted average of the neighbouring data samples. There are several variants of kriging that are used for surface fitting (for example, simple kriging, indicator kriging, etc.). Simple, ordinary and universal kriging (kriging with a trend) are the three types of kriging that could have been used in this study. Ordinary kriging is the most commonly used method and was considered to be best suited for this study based on the findings from a comparison between the three: Ordinary kriging was found to perform better than simple and universal kriging in areas where the data was sparse.
Before ordinary kriging could be performed the semivariance in the dataset needed to be computed to determine the weights used in the interpolation. The semivariance measures the spatial dependency between observations over specified distances (lags). The semivariance is defined as:
where
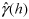 is the estimated semi-variance at a lag
is the estimated semi-variance at a lag
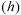 ,
,
 and
and
 are
the observed values at
are
the observed values at
 and
and
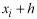 separated
by
separated
by
 , of which there are
, of which there are
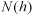 pairs (Borga and Vizzaccaro, 1997).
The
pairs (Borga and Vizzaccaro, 1997).
The
 for a given
for a given
 are graphed to produce what
is referred to as the empirical semivariogram where a continuous function
is fitted to the values to allow the prediction. The most commonly used function
is a spherical model defined as:
are graphed to produce what
is referred to as the empirical semivariogram where a continuous function
is fitted to the values to allow the prediction. The most commonly used function
is a spherical model defined as:
where
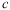 and
and
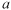 are the sill and range, respectively (Webster
and Oliver, 2000). The range characterizes the limit of
spatial dependence (spatial autocorrelation) between runoff values and is
defined by the sill, which indicates the level of maximum heterogeneity. The
range defined by the spherical model also determines the neighbourhood search
radius size used in kriging for locating neighbouring observations. Ordinary
kriging estimates the value of
are the sill and range, respectively (Webster
and Oliver, 2000). The range characterizes the limit of
spatial dependence (spatial autocorrelation) between runoff values and is
defined by the sill, which indicates the level of maximum heterogeneity. The
range defined by the spherical model also determines the neighbourhood search
radius size used in kriging for locating neighbouring observations. Ordinary
kriging estimates the value of
 at
at
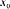 by
by
 using
a weighted average of surrounding values of the variable
using
a weighted average of surrounding values of the variable
 at
at
 as
follows:
as
follows:
where
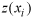 are the measured values at the ith
locations,
are the measured values at the ith
locations,
 is the prediction location,
is the prediction location,
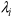 are the weights of the estimator that minimize the variance (that is,
are the weights of the estimator that minimize the variance (that is,
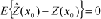 , where
, where
 is
the runoff expectation) and
is
the runoff expectation) and
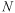 is the number of measured
values (Borga and Vizzaccaro, 1997; Webster and Oliver, 2000). The
spatial structure of the semivariogram is used to produce a kriging system
of linear equations combining neighbouring information as follows:
is the number of measured
values (Borga and Vizzaccaro, 1997; Webster and Oliver, 2000). The
spatial structure of the semivariogram is used to produce a kriging system
of linear equations combining neighbouring information as follows:
under the constraints of:
where
 is the Lagrange multiplier for the constraint
on the weights linked to the unbiased condition (St-Hilaire et al., 2003),
is the Lagrange multiplier for the constraint
on the weights linked to the unbiased condition (St-Hilaire et al., 2003),
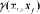 is
the semivariogram of
is
the semivariogram of
 between the data points
between the data points
 and
and
 ,
and
,
and
 is the semivariogram between
the ith observation and the estimates location
is the semivariogram between
the ith observation and the estimates location
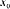 (Webster and Oliver, 2000). The weights
in ordinary kriging are forced
to sum to 1, so that the predictor, equation (3) is unbiased for
(Webster and Oliver, 2000). The weights
in ordinary kriging are forced
to sum to 1, so that the predictor, equation (3) is unbiased for
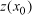 (Isaaks and Srivastava, 1989). 5
(Isaaks and Srivastava, 1989). 5
Prior to the construction of semivariograms the histograms of the monthly
runoff data were evaluated for normality. Ordinary kriging is known to be
optimal when the data follows a normal distribution (Armstrong and Boufassa, 1987)
because the underlying assumption of semivariogram analysis is that the distribution
of values approximates a normal distribution (Houlding, 2000). The runoff
data were found to be highly positively skewed with several values of zero
for runoff observations in the Prairies and the Arctic. To transform the data
to follow a normal distribution,
 was
applied with a constant value of 1 added to remove zero values.
Constant values of 1 or less are recommended because
high values can eliminate the advantage of the logarithmic transformation
(Yamamoto, 2007). Studies conducted by Wu et al, (2006) as well
as Kravchenko and Bullock, (1999) found that transforming highly skewed data
improved the results obtained from ordinary kriging.
was
applied with a constant value of 1 added to remove zero values.
Constant values of 1 or less are recommended because
high values can eliminate the advantage of the logarithmic transformation
(Yamamoto, 2007). Studies conducted by Wu et al, (2006) as well
as Kravchenko and Bullock, (1999) found that transforming highly skewed data
improved the results obtained from ordinary kriging.
The spatial arrangement of the monthly runoff data was also evaluated to determine how the observations were distributed over the extent of the study area because the interpolated surface varies according to the arrangement of the input data (Map 2).
The spatial structure of the data displayed a fairly dense network in the South with defined areas of clustering while the North exhibited a sparsely populated network. Since semivariogram models are characterized by the distance and degree of variability between observations, models developed to fit the whole dataset were not appropriate. It was also found that the runoff observations had some form of directionality that could be seen where the variability between runoff observations was more pronounced in a certain direction within specific clusters. These findings indicated that semivariogram models for individual regions would be more suitable. Through an evaluation of the physiographic characteristics where the points were clustered along with an overall assessment of the spatial arrangement, four zones were identified (Map 3).
Given that the dataset was divided into zones it was important to ensure the interpolation did not collapse at the zone divide, since kriging performs optimally when the area being predicted falls within a convex hull defined by the observations (Olea, 1999). To make certain this did not happen, points falling within a 300 km buffer around each zone were included to produce a smoother transition between zones and maintain the global trends. The distance of 300 km was found to be the most suitable distance because the data included in this buffer area was enough to ensure the interpolation performed properly at the zone divide. 6
After the data were assigned to each zone, the distribution of each dataset was checked for normality to ensure the division of the dataset did not create skewed datasets. Semivariograms were built for each zone of every month of the thirty years (1440 models) since the runoff observations can vary for each time period. The lag size for each semivariogram was set to the minimum average Euclidean distance between all points in the zone. 7 The approximate number of lags was determined based on how many lags multiplied by the lag size would equal approximately half the maximum Euclidean distance between observations since distances (lags) larger than the extent would not have any pairs. Spherical models were then fit to the semivariance clouds to determine the observations' range of influence by indicating the position at which samples became independent of each other (Chart 3).
As noted previously directionality was observed when splitting the dataset
into zones; therefore anisotropic semivariograms were calculated for zones 1, 2,
and 3. Anisotropy indicates that not all spatial directions are equivalent in their characteristics and the dependence between
 and
and
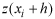 is
a function of both the magnitude
and direction of
is
a function of both the magnitude
and direction of
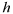 (Cressie, 1993) (that is, it is possible to fit different
semivariograms for different directions). For example in zone 1 the
runoff varies similarly over large distances in the South East – North
West direction corresponding to the runoff found in the Rocky Mountains. This
results in a larger range in the semivariogram fit in this direction (Figure 1). The anisotropy identified by the pattern of spatial
continuity also defined the search neighbourhood that limits the area to look
for nearby points. Typically the search neighbourhood is a circle (isotropic)
centred on the location being estimated, but when the variation is anisotropic
it is better to use an ellipse with the major axis oriented along the direction
of maximum continuity (Goovaerts, 1997). Zone 4 was treated
differently because of the sparse network of data. The direction exhibiting
the largest range in the semivariogram was used for the major and minor axis,
defining an isotropic search ellipse.
(Cressie, 1993) (that is, it is possible to fit different
semivariograms for different directions). For example in zone 1 the
runoff varies similarly over large distances in the South East – North
West direction corresponding to the runoff found in the Rocky Mountains. This
results in a larger range in the semivariogram fit in this direction (Figure 1). The anisotropy identified by the pattern of spatial
continuity also defined the search neighbourhood that limits the area to look
for nearby points. Typically the search neighbourhood is a circle (isotropic)
centred on the location being estimated, but when the variation is anisotropic
it is better to use an ellipse with the major axis oriented along the direction
of maximum continuity (Goovaerts, 1997). Zone 4 was treated
differently because of the sparse network of data. The direction exhibiting
the largest range in the semivariogram was used for the major and minor axis,
defining an isotropic search ellipse.
Ordinary kriging was then performed for each zone using the parameters
established from the semivariogram models. For each kriging prediction, a
corresponding standard error was calculated. The standard error provides a
measure of uncertainty that is dependent on the observations' spatial
arrangement and the semivariogram model (Houlding, 2000). The prediction
and standard error surfaces were output with a 10 km resolution.
Since the kriging procedure was performed in log-space, the predictions were
back-transformed to the original scale of the
data. The transformation is not a simple antilogarithm
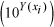 of the kriged prediction because this method
tends to inflate any errors
associated with the interpolation of the surface (Simard et al., 1992).
The back-transformation for the kriging estimate
of the kriged prediction because this method
tends to inflate any errors
associated with the interpolation of the surface (Simard et al., 1992).
The back-transformation for the kriging estimate
 is defined as:
is defined as:
where
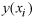 is the lognormal kriging prediction,
is the lognormal kriging prediction,
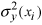 is
the corresponding lognormal variance,
is
the corresponding lognormal variance,
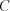 is the value of the constant added to the original data before transformation
and
is the value of the constant added to the original data before transformation
and
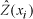 is the back-transformed data in the original scale of runoff (mm) (Gilbert, 1987; Deutsch
and Journel, 1998).
is the back-transformed data in the original scale of runoff (mm) (Gilbert, 1987; Deutsch
and Journel, 1998).
 is used because the (nonlinear) back-transformation of an unbiased estimate is not unbiased
itself, and in this case the introduction of
is used because the (nonlinear) back-transformation of an unbiased estimate is not unbiased
itself, and in this case the introduction of
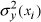 is
known to reduce the bias. Even though this back-transformation method can
produce a slight bias, it was considered to be practical for this study given
that there were 1440 prediction surfaces to back-transform. There
are more rigorous methods available that assert an unbiased back-transformation;
an example can be found in Yamamoto, (2007).
is
known to reduce the bias. Even though this back-transformation method can
produce a slight bias, it was considered to be practical for this study given
that there were 1440 prediction surfaces to back-transform. There
are more rigorous methods available that assert an unbiased back-transformation;
an example can be found in Yamamoto, (2007).
There was no straightforward approach for transforming the standard error to the scale of the original runoff data; as a result, the standard error is presented in logarithm space, providing a relative, not absolute comparison to the original runoff units.
2.4 Estimating the water yield
The monthly zones of interpolated runoff were merged and then summed to produce yearly surfaces. These yearly runoff surfaces were then averaged to produce the thirty-year surface and scaled back to a volume based on the resolution (100 km2) of the surfaces, producing the water yield estimate.
Knowing that the density of observations used to produce the kriging estimate is highly variable and sparse in certain areas, an assessment was made to determine if some time periods did not contain enough observations to be included in the thirty-year estimate. Evaluations of the standard error surfaces indicated areas where the kriging predictions are highly uncertain. For example the standard error map for January 1971 for zone 1 and 4 can be seen in Map 4 and 5, respectively.
It is clear from Map 4 and 5 that the standard error steadily increases from the observation locations. However the standard error and distance relationship found in zone 4 (Map 4) is very different from that found in zone 1 (Map 5). Clearly the fitted semivariogram strongly influences the level of standard error. The semivariogram model presented in Chart 3 indicates that observations in zone 1 are highly variable over short distances compared to zone 4, where the observations are similar over large distances. The corresponding kriged predictions for zone 1 and 4 were evaluated and it was concluded that the high standard error in zone 4 was related to data paucity and a good indication that artefacts 8 were being introduced in the predicted surface (Map 6), compared to zone 1 where the interpolation does not breakdown and the standard error indicates areas of uncertainty in the predicted surface (Map 7). The standard error and predicted surfaces for zones 2 and 3 were also assessed, but there were no artefacts in the predicted surfaces similar to those found in zone 4 and no localized spots of high uncertainty in the standard error surface comparable to zone 1.
To gain a further understanding with regards to how the density of points changes through the years, the average observation density per 10,000 km2 for each year was calculated for each zone by dividing the number of observations by the area of each zone (Chart 4). This provides a rough estimate of the density, but it does not consider the spatial arrangement (clustering) of observations in each zone. Chart 4 shows how zone 4 has a very low density compared to the other zones. It also indicates that density varies through time.
Both the standard error and data density findings indicated that it would be best to exclude certain areas where the data density was low or the standard error was high. However, it was not possible to define a standard error uncertainty cut-off for each predicted surface because the kriging standard error is semivariogram-dependent; therefore the standard error surfaces are not directly comparable. Although there were known levels of uncertainty in each predicted surface, the biggest concern was to remove the artefacts in the interpolation that were found in zone 4. The artefacts diminish from 1971 to 1976 when the data density increases (Chart 4). The artefacts almost become nonexistent from 1977 on, for the area below the Arctic Archipelago (Map 8).
From 1993 to 1996 the data density is reduced again, but the spatial arrangement is well distributed over the zone and there are no glaring artefacts. From 1997 to 2001 the observation density diminishes further and the favourably distributed arrangement is lost. For that reason, the thirty-year annual average for zone 4 only includes data from 1974 to 1997. To further improve zone 4, and given that the Arctic Archipelago is never free from artefacts, the research conducted by Spence and Burke, (2008) was input as a fixed value through the time series. This value (211 mm or 189 km3) is an annual average for twenty-three years from 1972 to 1994 and covers approximately 70 percent of the Arctic Archipelago (895,000 km2). This estimate is based on observations recorded between May and October because the data were too sparse during the winter months.
2.5 Validation of water yield estimates
The water yield methodology and final estimates were validated using two techniques. The first was an assessment of the stability of the water yield estimates, which was conducted by repetitively removing input data and observing how the interpolation performed. The second utilized measures of difference to quantify the amount of disagreement between the observed (HYDAT values divided by corresponding HYDEX or PFRA contributing areas) and predicted values of the runoff surfaces using a dataset withheld from the input data. The Arctic Archipelago was excluded from the validation process since the results from Spence and Burke, (2008) were used for this area.
2.5.1 Stability analysis
The stability of the water yield estimates was evaluated using a "bootstrapping" technique where the interpolation was run 100 times with a randomly selected 10 percent of the observations removed from each zone. This was performed in order to understand how the water yield estimates computed from the interpolated surfaces change with a reduced input dataset. This analysis was completed for every zone of each month for 1990, given that February 1990 contained the median number of observations in the database, which should give a good indication of the behaviour of the model in other years.
2.5.2 Measures of differences
The interpolated surfaces (runoff depths) were further assessed by calculating the mean error (ME), and root mean square error (RMSE) as follows:
where
 is the observed (known) value, and
is the observed (known) value, and
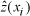 is
the predicted value. The ME should equal zero if the interpolation method is unbiased. The RMSE provides a measure
of the accuracy where again the ideal value would be zero. These difference
measures were calculated using data that met all the criteria to be entered
into the database (as presented in Section 2.1.1) except that the corresponding
contributing area of these observations is greater than 5000 km2. The validation dataset contained 89 gauging stations with
basin sizes ranging from 5020 km2 to 9890 km2. Map 9 displays
the location of these validation observations. A scatter plot was also produced
of
is
the predicted value. The ME should equal zero if the interpolation method is unbiased. The RMSE provides a measure
of the accuracy where again the ideal value would be zero. These difference
measures were calculated using data that met all the criteria to be entered
into the database (as presented in Section 2.1.1) except that the corresponding
contributing area of these observations is greater than 5000 km2. The validation dataset contained 89 gauging stations with
basin sizes ranging from 5020 km2 to 9890 km2. Map 9 displays
the location of these validation observations. A scatter plot was also produced
of
 versus
versus
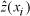 for
every data point used in the validation for every time period (n=19583). The
difference measures assume the observed values are not in error.
for
every data point used in the validation for every time period (n=19583). The
difference measures assume the observed values are not in error.
3 Results
3.1 Water yield estimates
A thirty-year annual water yield estimate of 3435 km3/yr was calculated for Canada. The thirty-year annual average runoff depth surfaces that were used to produce the water yield estimate can be seen in Maps 10, 11, 12 and 13.
3.2 Validation
3.2.1 Stability analysis
The stability analysis indicated that the water yield estimate had a maximum range of 96 km3 for the annual average water yield for 1990 (excluding the Arctic Archipelago) with 10 percent of the observations randomly removed from each zone, for all months (Chart 5). The average water yield predicted was 3265 km3 (Chart 6), the actual estimate was 3273 km3. The maximum range of 96 km3 corresponds to 2.9 % of the 3273 km3 estimate.
Chart 7 demonstrates that May, June and July are the largest contributors to the instability in the yearly yield estimates in 1990. This is explained by the fact that, nationally, this period represents the highest yields and therefore, the highest potential for variation.
Chart 8 indicates that the highest variability in the yield estimate for June occurred in zone 4 (range = 126.5 km3) followed by zone 1 (range = 10 km3). Zone 4 is highly variable because the data is very sparse throughout the zone with the majority of the observations clustered along the southern border. The range found in Zone 1 is related to the high variability between runoff observations. Some observations are very high or low in relation to the neighbouring observations. When these extreme values are included or excluded the estimate will vary. The estimates for zone 2 and zone 3 remained fairly constant with a range of 1.2 km3 and 5.7 km3, respectively.
3.2.2 Measures of difference
The results for the ME and RMSE can be seen in Charts 9 and 10 and Charts 11 and 12, respectively. The charts reveal
that the runoff predicted values are on average higher than the observed values
(negative ME), especially for May, June, and July throughout the thirty-years.
The differences are thought to be caused by the greater variability in runoff
during these months, since there is likely localized changes that are not
included in the surrounding runoff observations that determine the predicted
value. Overall the measures of difference indicated that the predicted surfaces
are within a reasonable range of the validation values with the main differences
occurring during months when the runoff is known to be highly variable. The
scatter plot produced had a strong correlation (r = 0.78, p 0.001) between all the observed and predicted values (n=19583)
used in the validation dataset over the whole thirty-years of data (Figure 2).
0.001) between all the observed and predicted values (n=19583)
used in the validation dataset over the whole thirty-years of data (Figure 2).
Figure 2: Predicted versus observed runoff depth at validation stations, 1971 to 2000
4 Conclusion and future direction
This paper presented a detailed description of the Statistics Canada methodology to produce a thirty-year annual estimate of water yield for Canada. The results from this study found that the average annual thirty-year water yield for Canada from 1971 to 2000 was 3435 km3. This is the first comprehensive estimate of freshwater flow at the national level using a systematic semi-automated methodology consistently applied across the country.
The final estimate was validated using two approaches. The first tested the stability of the water yield model when 10 percent of the data was repetitively removed from the model. The stability analysis indicated that the interpolation of the runoff surfaces was generally stable with the highest instability occurring in May, June and July. The paucity of observations in zone 4 was the main reason for the variability in the yield estimates especially for months exhibiting high flow.
The second approach showed how the observed and predicted runoff values differ over the extent of the study area, using a set of validation sites and providing an approximation of the error in the interpolation. It also indicated that the main differences between the observed and predicted runoff took place during May, June and July. It was found during this validation that some basins had predictions higher than the observed runoff, especially in zone 1 where flow can be "flashy". In these few instances, runoff values used in the interpolation from neighbouring basins did not always completely reflect the flow regimes within the predicted basin.
The water yield estimate produced by this methodology is considered to provide a reasonable estimate at the national scale, suitable for filling a significant gap in the freshwater asset accounts. However, given the challenges of estimating from a sparse network of hydrometric observations (especially in the North), there are several areas for future research. For example, additional research in identifying a statistically representative national gauging network is warranted in order to further improve the current estimate. This will also minimize the potential bias that can be associated with the use of certain gauged basins since they belong to gauging programs that have particular objectives that may not consider capturing the main flow regime for a given region.
Further research will also be required to determine how the water yield predictions can be utilized for regional assessments or trend analysis given there are several locations containing high levels of uncertainty, especially in zone 4 and some areas of zone 1. More research is necessary to determine if the standard error (variance) of the prediction can be back-transformed to the original scale of the data, which would allow direct comparison of the error to the kriging predictions. The standard error could then be used to construct confidence intervals of the prediction and used to determine significant differences between time periods in a time series analysis. Research should also be carried out to determine if the standard error could establish a cut-off at which the prediction is too uncertain to provide an estimate of water yield at a regional level.
Notwithstanding these concerns, an index of variability was calculated for zones 1, 2, and 3 to provide some insight into where the highest relative variability in runoff was occurring through the thirty-year time series, compared to the thirty-year average (Map 14). The index for each grid cell was calculated for the thirty-years covering the study period, by dividing the standard deviation by the mean. The index indicates regions where there is a high variability, directing us in future research to determine if the variability is a result of year to year fluctuations in runoff or a tendency towards an increase or decrease over time.
In addition, preliminary steps have been taken to evaluate the volumes predicted and observed at a basin scale through hydrograph comparisons. The results from this analysis will be released when an assessment of the yields at a regional scale is completed. The main focus of this paper was to present the methodology used to produce the thirty-year annual average water yield estimate. Additional work will be necessary if the water yield is to be explained on a regional basis.
- Date modified: