Latest Developments in the Canadian Economic Accounts
Seasonal adjustment of stocks and flows in the Financial and Wealth Accounts: towards an integrated approach
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
Skip to text
Text begins
Correction notice
The appendix has been updated to include a correction to the formula for the calculation of seasonally adjusted OCA.
Introduction
The Financial and Wealth Accounts (FWA) contain a comprehensive accounting of Canada’s financial and non-financial wealth. The FWA is composed of the National Balance Sheet Account (NBSA), which measures the stock of financial assets and liabilities, the Financial Flow Account (FFA), which measures the net transactions in these same instruments, and the Other Changes in Assets Account (OCAA), which measures the revaluation of existing stocks due to price changes as well as other volume changes. In other words, these accounts generate a breakdown of the financial flows that increase and decrease an institutional sector’s wealth, that is, the market value of assets and liabilities at a point in time. These accounts are produced on a quarterly basis.
In the FWA there is a direct relationship between the previous and current period’s closing stocks with the accumulation of financial flows, (i.e., net financial transactions, revaluations due to price effects, and other volume changes) accounting for the difference (see Box 1). Additionally, this stock-flow identity must be maintained throughout the time series and ensures that all three accounts are consistent and coherent. For further information on the FWA please see the User Guide to the Canadian System of National Accounts, Chapter 7.
Start of text boxwhere,
= stock position of instrument at time t, found in the NBSA;
= stock position of instrument at time t-1, found in the NBSA;
= net transaction flow of instrument at time t, found in the FFA;
= other change in asset of instrument at time t, found in the OCAA.
The principal motivation in producing estimates of seasonally adjusted household sector borrowing arose as a result of the observed seasonality present in the unadjusted credit market debt estimates. For example, Canadians tend to borrow more in the form of consumer credit in the fourth quarter, with the arrival of significant retail activity tied to the holidays, and then subsequently cut back in the first quarter. Moreover, mortgage borrowing has a tendency to slow down in the first quarter, but then pick up in the second and third quarters with an increase in resale activity as winter recedes in many areas of Canada and families look to secure housing before the start of the upcoming school year. This phenomena of sub-annual cyclical patterns is not constrained to the household sector and can be seen in other areas such as government borrowing. Consequently, seasonal adjustment in this context enhances the interpretability of estimates that possess a strong cyclical component, eliminating the variation due to predictable and recurrent patterns. This provides data users, policy makers, and researchers with more accurate quarter-to-quarter movements that reveal the underlying trends in the data. While only household borrowing is the current area of interest, seasonal adjustment will eventually be expanded to encompass other selected sectors in the FWA. However, the intention is not to seasonally adjust all instruments and sectors.
The seasonally adjusted estimates of borrowing that are currently available in the FWA focus on the financial transactions of households. As such, the seasonality that is also present in the stock of household debt is not accounted for, given that this stock accumulates unadjusted financial transactions. In order to ensure a coherent framework in the FWA it is desirable to have an integrated approach to seasonally adjusting both stocks and flows. This is because the stock-flow identify must hold whether the data is seasonally adjusted or not and a unified framework for the former helps facilitate this outcome.
One consequence of the lack of seasonally adjusted stocks involves the ratio of household credit market debt to disposable income, which contains seasonality as a by-product of its unadjusted components (see Chart 1). Given this result, it is common for users to misinterpret certain quarters as record highs in the ratio even though this is simply due to a predictable cyclical trend. Users closely monitor this ratio, among others, as an indicator of vulnerability in the household sector. This underscores the importance of accurately assessing the quarterly trends in household indebtedness.

Data table for Chart 1
| Ratio of published unadjusted ratio of credit market debt to disposable income | |
|---|---|
| percent | |
| 2010 | |
| First quarter | 155.2 |
| Second quarter | 156.9 |
| Third quarter | 158.0 |
| Fourth quarter | 158.3 |
| 2011 | |
| First quarter | 157.2 |
| Second quarter | 158.4 |
| Third quarter | 159.1 |
| Fourth quarter | 159.5 |
| 2012 | |
| First quarter | 158.5 |
| Second quarter | 159.8 |
| Third quarter | 160.4 |
| Fourth quarter | 160.2 |
| 2013 | |
| First quarter | 159.7 |
| Second quarter | 160.5 |
| Third quarter | 161.1 |
| Fourth quarter | 160.7 |
| 2014 | |
| First quarter | 160.2 |
| Second quarter | 161.2 |
| Third quarter | 162.4 |
| Fourth quarter | 162.4 |
| 2015 | |
| First quarter | 161.5 |
| Second quarter | 162.9 |
| Third quarter | 164.1 |
| Fourth quarter | 164.8 |
| 2016 | |
| First quarter | 166.5 |
| Second quarter | 170.1 |
| Third quarter | 172.2 |
| Fourth quarter | 173.3 |
| 2017 | |
| First quarter | 172.7 |
| Second quarter | 174.1 |
| Third quarter | 174.3 |
| Fourth quarter | 173.8 |
| 2018 | |
| First quarter | 172.3 |
| Second quarter | 173.2 |
| Third quarter | 173.8 |
|
Source: Statistics Canada, "Seasonal adjustment of stocks and flows in the Financial and Wealth Accounts: towards an integrated approach", Latest Developments in the Canadian Economic Accounts (13-605-X), 2018. |
|
Seasonal adjustment is a technique that aims to identify, estimate and remove seasonal variations in a time series. These variations result from the effects of institutional and climatic factors and are expected to reoccur at the same time of the year with similar intensities. Seasonally adjusted time series contains the trend cycle and irregular components. This provides an approximate idea of the underlying changes in trends and facilitates the analysis of short-term dynamics.
For more information on seasonal adjustment: Seasonally adjusted data – Frequently asked questions
For these reasons, Statistics Canada initiated a project to explore various methods to produce an integrated set of seasonally adjusted financial flows, stocks, and other changes in assets that could be utilized in the FWA in general, and more specifically, to produce a coherent set of estimates for household credit market debt that could be leveraged to derive useful financial indicators.
Approach to the seasonal adjustment of stocks and flows
Generally, time series can be categorized into two different types: stock and flow. A stock series is a measure of the magnitude of attributes at a specific point in time, while a flow series refers to the accumulated value over a period of time. In the FWA, the NBSA records the stock or value of assets and liabilities at the end of the quarter while the FFA and the OCAA record flows over the quarter.
After experimenting with various models and assumptions and through consultations with experts and users, it was determined that the most practical approach involved: 1) directly seasonally adjusting a stock version of the unadjusted OCAA, 2) directly seasonally adjusting the unadjusted NBSA stocks after removing the unadjusted OCAA, and 3) indirectly deriving the seasonally adjusted FFA flows from the NBSA stocks. These specific steps are detailed in the appendix.
This approach was adopted for each component of household credit market debt including mortgage loans, non-mortgage loans, and consumer credit. The resulting seasonally adjusted series were then aggregated to produce an estimate of total credit market debt.
Results
Selected results from the integrated FWA approach to seasonal adjustment are presented below. These data are available in table 38-10-0238.
Seasonally adjusted household borrowing, credit market debt flows
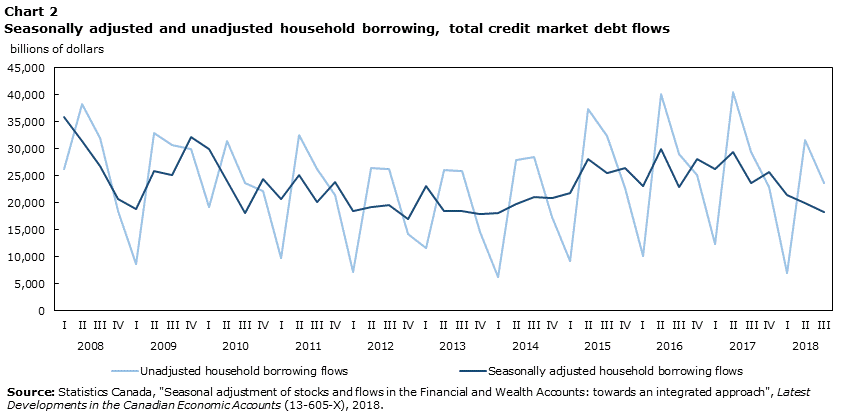
Chart 2 shows that the seasonally adjusted financial flows for total credit market debt cut through the unadjusted estimates, preserving the average level of the unadjusted estimates over time. The unadjusted series show large declines in the first quarter of each year with a subsequent spike in the second and third quarters. By comparison, in the first quarter of 2018, the seasonally adjusted flows decreased by $4.2 billion while the unadjusted estimates declined $15.9 billion.
Data table for Chart 2
| Unadjusted household borrowing flows | Seasonally adjusted household borrowing flows | |
|---|---|---|
| billions of dollars | ||
| 2008 | ||
| First quarter | 26,247 | 35,967 |
| Second quarter | 38,218 | 31,448 |
| Third quarter | 32,067 | 26,844 |
| Fourth quarter | 18,491 | 20,684 |
| 2009 | ||
| First quarter | 8,746 | 18,887 |
| Second quarter | 32,886 | 25,814 |
| Third quarter | 30,715 | 25,212 |
| Fourth quarter | 29,898 | 32,158 |
| 2010 | ||
| First quarter | 19,182 | 29,905 |
| Second quarter | 31,505 | 24,008 |
| Third quarter | 23,688 | 18,079 |
| Fourth quarter | 22,167 | 24,430 |
| 2011 | ||
| First quarter | 9,771 | 20,697 |
| Second quarter | 32,541 | 25,233 |
| Third quarter | 26,351 | 20,173 |
| Fourth quarter | 21,442 | 23,898 |
| 2012 | ||
| First quarter | 7,298 | 18,498 |
| Second quarter | 26,468 | 19,189 |
| Third quarter | 26,291 | 19,529 |
| Fourth quarter | 14,277 | 17,075 |
| 2013 | ||
| First quarter | 11,577 | 23,206 |
| Second quarter | 26,166 | 18,582 |
| Third quarter | 25,930 | 18,568 |
| Fourth quarter | 14,545 | 17,984 |
| 2014 | ||
| First quarter | 6,245 | 18,209 |
| Second quarter | 28,020 | 19,720 |
| Third quarter | 28,435 | 21,137 |
| Fourth quarter | 17,346 | 20,929 |
| 2015 | ||
| First quarter | 9,217 | 21,774 |
| Second quarter | 37,351 | 28,110 |
| Third quarter | 32,343 | 25,446 |
| Fourth quarter | 22,830 | 26,376 |
| 2016 | ||
| First quarter | 10,236 | 23,202 |
| Second quarter | 40,118 | 30,025 |
| Third quarter | 29,114 | 22,948 |
| Fourth quarter | 25,217 | 28,215 |
| 2017 | ||
| First quarter | 12,376 | 26,187 |
| Second quarter | 40,443 | 29,409 |
| Third quarter | 29,384 | 23,690 |
| Fourth quarter | 22,988 | 25,718 |
| 2018 | ||
| First quarter | 7,115 | 21,489 |
| Second quarter | 31,684 | 20,014 |
| Third quarter | 23,668 | 18,272 |
| Source: Statistics Canada, "Seasonal adjustment of stocks and flows in the Financial and Wealth Accounts: towards an integrated approach", Latest Developments in the Canadian Economic Accounts (13-605-X), 2018. | ||
Seasonally adjusted household borrowing, total credit market debt levels
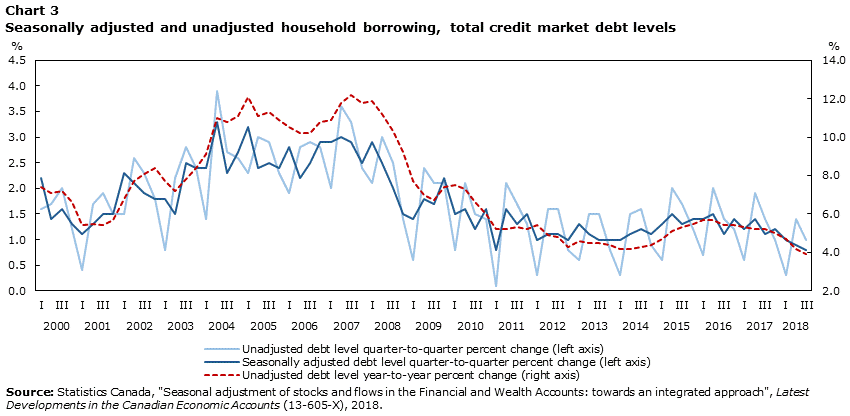
As with the financial flows, the growth rate of the unadjusted stock of household debt shows a similar seasonal pattern with the growth rate of the seasonally adjusted series again cutting through the former. By comparison, the year-over-year growth rate displays long-term trends similar to the seasonally adjusted growth, but does not provide as reliable an indication of current period trends.
Data table for Chart 3
| Unadjusted debt level quarter-to-quarter percent change (left axis) | Seasonally adjusted debt level quarter-to-quarter percent change (left axis) | Unadjusted debt level year-to-year percent change (right axis) | |
|---|---|---|---|
| percent | |||
| 2000 | |||
| First quarter | 1.6 | 2.2 | 7.4 |
| Second quarter | 1.7 | 1.4 | 7.1 |
| Third quarter | 2.0 | 1.6 | 7.2 |
| Fourth quarter | 1.2 | 1.3 | 6.6 |
| 2001 | |||
| First quarter | 0.4 | 1.1 | 5.4 |
| Second quarter | 1.7 | 1.3 | 5.5 |
| Third quarter | 1.9 | 1.5 | 5.4 |
| Fourth quarter | 1.5 | 1.5 | 5.7 |
| 2002 | |||
| First quarter | 1.5 | 2.3 | 6.8 |
| Second quarter | 2.6 | 2.1 | 7.7 |
| Third quarter | 2.3 | 1.9 | 8.1 |
| Fourth quarter | 1.8 | 1.8 | 8.4 |
| 2003 | |||
| First quarter | 0.8 | 1.8 | 7.7 |
| Second quarter | 2.2 | 1.5 | 7.2 |
| Third quarter | 2.8 | 2.5 | 7.8 |
| Fourth quarter | 2.4 | 2.4 | 8.4 |
| 2004 | |||
| First quarter | 1.4 | 2.4 | 9.1 |
| Second quarter | 3.9 | 3.3 | 11.0 |
| Third quarter | 2.7 | 2.3 | 10.8 |
| Fourth quarter | 2.6 | 2.7 | 11.1 |
| 2005 | |||
| First quarter | 2.3 | 3.2 | 12.1 |
| Second quarter | 3.0 | 2.4 | 11.1 |
| Third quarter | 2.9 | 2.5 | 11.3 |
| Fourth quarter | 2.3 | 2.4 | 10.9 |
| 2006 | |||
| First quarter | 1.9 | 2.8 | 10.5 |
| Second quarter | 2.8 | 2.2 | 10.2 |
| Third quarter | 2.9 | 2.5 | 10.2 |
| Fourth quarter | 2.8 | 2.9 | 10.8 |
| 2007 | |||
| First quarter | 2.0 | 2.9 | 10.9 |
| Second quarter | 3.6 | 3.0 | 11.8 |
| Third quarter | 3.3 | 2.9 | 12.2 |
| Fourth quarter | 2.4 | 2.5 | 11.8 |
| 2008 | |||
| First quarter | 2.1 | 2.9 | 11.9 |
| Second quarter | 3.0 | 2.5 | 11.2 |
| Third quarter | 2.5 | 2.0 | 10.3 |
| Fourth quarter | 1.4 | 1.5 | 9.2 |
| 2009 | |||
| First quarter | 0.6 | 1.4 | 7.7 |
| Second quarter | 2.4 | 1.8 | 7.0 |
| Third quarter | 2.1 | 1.7 | 6.7 |
| Fourth quarter | 2.1 | 2.2 | 7.4 |
| 2010 | |||
| First quarter | 0.8 | 1.5 | 7.5 |
| Second quarter | 2.1 | 1.6 | 7.3 |
| Third quarter | 1.5 | 1.2 | 6.6 |
| Fourth quarter | 1.4 | 1.6 | 6.0 |
| 2011 | |||
| First quarter | 0.1 | 0.8 | 5.2 |
| Second quarter | 2.1 | 1.6 | 5.2 |
| Third quarter | 1.7 | 1.3 | 5.3 |
| Fourth quarter | 1.3 | 1.5 | 5.2 |
| 2012 | |||
| First quarter | 0.3 | 1.0 | 5.4 |
| Second quarter | 1.6 | 1.1 | 4.9 |
| Third quarter | 1.6 | 1.1 | 4.8 |
| Fourth quarter | 0.8 | 1.0 | 4.3 |
| 2013 | |||
| First quarter | 0.6 | 1.3 | 4.6 |
| Second quarter | 1.5 | 1.1 | 4.5 |
| Third quarter | 1.5 | 1.0 | 4.5 |
| Fourth quarter | 0.8 | 1.0 | 4.4 |
| 2014 | |||
| First quarter | 0.3 | 1.0 | 4.2 |
| Second quarter | 1.5 | 1.1 | 4.2 |
| Third quarter | 1.6 | 1.2 | 4.3 |
| Fourth quarter | 0.9 | 1.1 | 4.4 |
| 2015 | |||
| First quarter | 0.6 | 1.3 | 4.7 |
| Second quarter | 2.0 | 1.5 | 5.1 |
| Third quarter | 1.7 | 1.3 | 5.3 |
| Fourth quarter | 1.2 | 1.4 | 5.5 |
| 2016 | |||
| First quarter | 0.7 | 1.4 | 5.7 |
| Second quarter | 2.0 | 1.5 | 5.7 |
| Third quarter | 1.4 | 1.1 | 5.4 |
| Fourth quarter | 1.2 | 1.4 | 5.4 |
| 2017 | |||
| First quarter | 0.6 | 1.2 | 5.3 |
| Second quarter | 1.9 | 1.4 | 5.2 |
| Third quarter | 1.4 | 1.1 | 5.2 |
| Fourth quarter | 1.0 | 1.2 | 5.0 |
| 2018 | |||
| First quarter | 0.3 | 1.0 | 4.7 |
| Second quarter | 1.4 | 0.9 | 4.2 |
| Third quarter | 1.0 | 0.8 | 3.9 |
| Source: Statistics Canada, "Seasonal adjustment of stocks and flows in the Financial and Wealth Accounts: towards an integrated approach", Latest Developments in the Canadian Economic Accounts (13-605-X), 2018. | |||
Seasonally adjusted credit market debt as a proportion of disposable income
Until now, the Canadian measure of credit market debt as a proportion of disposable income was calculated as total household credit market debt divided by a four quarter moving sum of household disposable income (HDI). This approach was used to help reduce the seasonality present in the unadjusted HDI and to put the income on the same base as the debt (i.e., an annual estimate of income equivalent to the end-of-year stock).
Start of text boxIn Canada, total credit market debt for the household sector is defined by the sum of consumer credit, mortgage debt and non-mortgage loan liabilities. A useful indicator of households’ financial strength is the ratio of this debt burden relative to annual disposable income.
Chart 4 shows the seasonally adjusted ratio of credit market debt-to-disposable income. This ratio incorporates two principal changes: 1) it is now using the seasonally adjusted debt level as the numerator, and, 2) it is using the seasonally adjusted household disposable income at annual rates (SAAR HDI).

Data table for Chart 4
| Seasonally adjusted ratio of credit market debt to disposable income (left axis) | Published unadjusted ratio of credit market debt to disposable income (left axis) | Revisions (right axis) | |
|---|---|---|---|
| percent | |||
| 2000 | |||
| First quarter | 105.6 | 110.4 | 4.7 |
| Second quarter | 105.7 | 110.1 | 4.3 |
| Third quarter | 106.0 | 109.4 | 3.4 |
| Fourth quarter | 105.3 | 109.0 | 3.6 |
| 2001 | |||
| First quarter | 104.0 | 106.8 | 2.8 |
| Second quarter | 104.9 | 110.4 | 5.5 |
| Third quarter | 105.8 | 109.1 | 3.3 |
| Fourth quarter | 106.6 | 109.8 | 3.2 |
| 2002 | |||
| First quarter | 107.4 | 110.6 | 3.2 |
| Second quarter | 108.8 | 112.6 | 3.8 |
| Third quarter | 110.1 | 112.8 | 2.7 |
| Fourth quarter | 110.9 | 113.8 | 2.9 |
| 2003 | |||
| First quarter | 111.0 | 114.1 | 3.1 |
| Second quarter | 112.0 | 116.5 | 4.5 |
| Third quarter | 114.2 | 119.0 | 4.7 |
| Fourth quarter | 116.2 | 120.4 | 4.3 |
| 2004 | |||
| First quarter | 116.9 | 121.7 | 4.8 |
| Second quarter | 120.1 | 122.7 | 2.6 |
| Third quarter | 121.6 | 124.1 | 2.6 |
| Fourth quarter | 122.9 | 126.8 | 3.9 |
| 2005 | |||
| First quarter | 124.5 | 131.4 | 6.9 |
| Second quarter | 127.0 | 131.5 | 4.5 |
| Third quarter | 129.2 | 133.9 | 4.7 |
| Fourth quarter | 130.5 | 134.7 | 4.2 |
| 2006 | |||
| First quarter | 130.4 | 134.3 | 4.0 |
| Second quarter | 132.2 | 137.1 | 4.9 |
| Third quarter | 134.0 | 136.8 | 2.8 |
| Fourth quarter | 135.4 | 138.2 | 2.8 |
| 2007 | |||
| First quarter | 136.6 | 139.2 | 2.6 |
| Second quarter | 139.6 | 143.8 | 4.2 |
| Third quarter | 142.0 | 147.2 | 5.2 |
| Fourth quarter | 143.2 | 148.4 | 5.2 |
| 2008 | |||
| First quarter | 145.0 | 149.9 | 4.9 |
| Second quarter | 147.2 | 151.0 | 3.8 |
| Third quarter | 147.9 | 151.1 | 3.2 |
| Fourth quarter | 148.1 | 153.7 | 5.6 |
| 2009 | |||
| First quarter | 148.4 | 156.5 | 8.0 |
| Second quarter | 151.4 | 158.5 | 7.1 |
| Third quarter | 154.3 | 158.2 | 3.9 |
| Fourth quarter | 156.5 | 159.4 | 3.0 |
| 2010 | |||
| First quarter | 155.2 | 158.1 | 2.9 |
| Second quarter | 156.9 | 162.6 | 5.8 |
| Third quarter | 158.0 | 162.0 | 4.0 |
| Fourth quarter | 158.3 | 161.6 | 3.2 |
| 2011 | |||
| First quarter | 157.2 | 162.0 | 4.8 |
| Second quarter | 158.4 | 164.0 | 5.6 |
| Third quarter | 159.1 | 164.5 | 5.3 |
| Fourth quarter | 159.5 | 163.7 | 4.2 |
| 2012 | |||
| First quarter | 158.5 | 164.0 | 5.5 |
| Second quarter | 159.8 | 165.1 | 5.4 |
| Third quarter | 160.4 | 164.9 | 4.5 |
| Fourth quarter | 160.2 | 165.3 | 5.1 |
| 2013 | |||
| First quarter | 159.7 | 163.9 | 4.2 |
| Second quarter | 160.5 | 164.7 | 4.2 |
| Third quarter | 161.1 | 165.4 | 4.4 |
| Fourth quarter | 160.7 | 165.2 | 4.5 |
| 2014 | |||
| First quarter | 160.2 | 165.7 | 5.5 |
| Second quarter | 161.2 | 166.6 | 5.4 |
| Third quarter | 162.4 | 165.8 | 3.4 |
| Fourth quarter | 162.4 | 167.1 | 4.7 |
| 2015 | |||
| First quarter | 161.5 | 164.8 | 3.4 |
| Second quarter | 162.9 | 166.4 | 3.5 |
| Third quarter | 164.1 | 167.8 | 3.7 |
| Fourth quarter | 164.8 | 170.5 | 5.7 |
| 2016 | |||
| First quarter | 166.5 | 175.6 | 9.0 |
| Second quarter | 170.1 | 176.4 | 6.3 |
| Third quarter | 172.2 | 176.1 | 3.9 |
| Fourth quarter | 173.3 | 176.7 | 3.4 |
| 2017 | |||
| First quarter | 172.7 | 178.2 | 5.5 |
| Second quarter | 174.1 | 177.8 | 3.7 |
| Third quarter | 174.3 | 176.5 | 2.1 |
| Fourth quarter | 173.8 | 176.3 | 2.5 |
| 2018 | |||
| First quarter | 172.3 | 177.8 | 5.5 |
| Second quarter | 173.2 | 177.4 | 4.3 |
| Third quarter | 173.8 | 177.5 | 3.7 |
| Source: Statistics Canada, "Seasonal adjustment of stocks and flows in the Financial and Wealth Accounts: towards an integrated approach", Latest Developments in the Canadian Economic Accounts (13-605-X), 2018. | |||
Using the seasonally adjusted estimate of household disposable income at annual rates (SAAR HDI) is reasonable for a number of reasons. Firstly, it is already a key estimate published as part of the Income and Expenditure Accounts in which seasonally adjusted series are used to analyze quarterly movements, especially when gauging the evolving financial vulnerability of households. Moreover, it also provides for a more consistent calculation of financial ratios with the incorporation of a standardized income denominator.
An obvious caveat of using SAAR HDI is that more volatility is present in the ratio compared with simply using a moving sum. However, the SAAR HDI may more accurately reflect the quarter-to-quarter trends in HDI and represents the full weight of HDI in the ratio for a given quarter rather than averaging several quarters together.
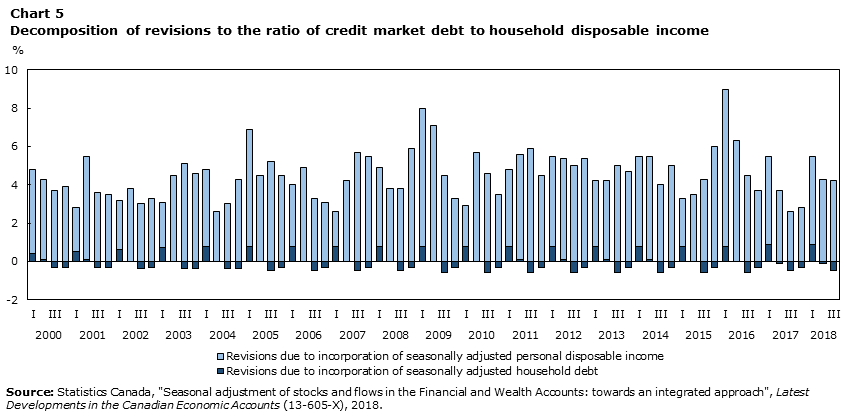
If we decompose the revisions to the ratio due to the introduction of seasonally adjusted household debt versus the incorporation of a new HDI denominator (see Chart 5) then two results are evident. Firstly, the revisions arising from using seasonally adjusted debt reflect the seasonality being removed from the ratio and their variability is quite minimal. Secondly, with the introduction of the SAAR HDI it is clear that the revisions are relatively more significant and variable. An important conclusion is that even though the ratio is seasonally adjusted it is still subject to large swings and volatility that is not attributable to seasonal factors, but rather movements in the level of seasonally adjusted income.
Data table for Chart 5
| Revisions due to incorporation of seasonally adjusted houdehold debt | Revisions due to incorporation of seasonally adjusted personal disposable income | |
|---|---|---|
| percent | ||
| 2000 | ||
| First quarter | 0.4 | 4.4 |
| Second quarter | 0.1 | 4.2 |
| Third quarter | -0.3 | 3.7 |
| Fourth quarter | -0.3 | 3.9 |
| 2001 | ||
| First quarter | 0.5 | 2.3 |
| Second quarter | 0.1 | 5.4 |
| Third quarter | -0.3 | 3.6 |
| Fourth quarter | -0.3 | 3.5 |
| 2002 | ||
| First quarter | 0.6 | 2.6 |
| Second quarter | 0.0 | 3.8 |
| Third quarter | -0.4 | 3.0 |
| Fourth quarter | -0.3 | 3.3 |
| 2003 | ||
| First quarter | 0.7 | 2.4 |
| Second quarter | 0.0 | 4.5 |
| Third quarter | -0.4 | 5.1 |
| Fourth quarter | -0.4 | 4.6 |
| 2004 | ||
| First quarter | 0.8 | 4.0 |
| Second quarter | 0.0 | 2.6 |
| Third quarter | -0.4 | 3.0 |
| Fourth quarter | -0.4 | 4.3 |
| 2005 | ||
| First quarter | 0.8 | 6.1 |
| Second quarter | 0.0 | 4.5 |
| Third quarter | -0.5 | 5.2 |
| Fourth quarter | -0.3 | 4.5 |
| 2006 | ||
| First quarter | 0.8 | 3.2 |
| Second quarter | 0.0 | 4.9 |
| Third quarter | -0.5 | 3.3 |
| Fourth quarter | -0.3 | 3.1 |
| 2007 | ||
| First quarter | 0.8 | 1.8 |
| Second quarter | 0.0 | 4.2 |
| Third quarter | -0.5 | 5.7 |
| Fourth quarter | -0.3 | 5.5 |
| 2008 | ||
| First quarter | 0.8 | 4.1 |
| Second quarter | 0.0 | 3.8 |
| Third quarter | -0.5 | 3.8 |
| Fourth quarter | -0.3 | 5.9 |
| 2009 | ||
| First quarter | 0.8 | 7.2 |
| Second quarter | 0.0 | 7.1 |
| Third quarter | -0.6 | 4.5 |
| Fourth quarter | -0.3 | 3.3 |
| 2010 | ||
| First quarter | 0.8 | 2.1 |
| Second quarter | 0.0 | 5.7 |
| Third quarter | -0.6 | 4.6 |
| Fourth quarter | -0.3 | 3.5 |
| 2011 | ||
| First quarter | 0.8 | 4.0 |
| Second quarter | 0.1 | 5.5 |
| Third quarter | -0.6 | 5.9 |
| Fourth quarter | -0.3 | 4.5 |
| 2012 | ||
| First quarter | 0.8 | 4.7 |
| Second quarter | 0.1 | 5.3 |
| Third quarter | -0.6 | 5.0 |
| Fourth quarter | -0.3 | 5.4 |
| 2013 | ||
| First quarter | 0.8 | 3.4 |
| Second quarter | 0.1 | 4.1 |
| Third quarter | -0.6 | 5.0 |
| Fourth quarter | -0.3 | 4.7 |
| 2014 | ||
| First quarter | 0.8 | 4.7 |
| Second quarter | 0.1 | 5.4 |
| Third quarter | -0.6 | 4.0 |
| Fourth quarter | -0.3 | 5.0 |
| 2015 | ||
| First quarter | 0.8 | 2.5 |
| Second quarter | 0.0 | 3.5 |
| Third quarter | -0.6 | 4.3 |
| Fourth quarter | -0.3 | 6.0 |
| 2016 | ||
| First quarter | 0.8 | 8.2 |
| Second quarter | 0.0 | 6.3 |
| Third quarter | -0.6 | 4.5 |
| Fourth quarter | -0.3 | 3.7 |
| 2017 | ||
| First quarter | 0.9 | 4.6 |
| Second quarter | -0.1 | 3.7 |
| Third quarter | -0.5 | 2.6 |
| Fourth quarter | -0.3 | 2.8 |
| 2018 | ||
| First quarter | 0.9 | 4.6 |
| Second quarter | -0.1 | 4.3 |
| Third quarter | -0.5 | 4.2 |
|
Source: Statistics Canada, "Seasonal adjustment of stocks and flows in the Financial and Wealth Accounts: towards an integrated approach", Latest Developments in the Canadian Economic Accounts (13-605-X), 2018. |
||
Conclusion
The objective of this paper was to document the consideration given in identifying a suitable method for the integrated seasonal adjustment of stocks and flows in the FWA as well as present an overview of the results of this method. This approach is intended to be generalized within the FWA so that selected series containing seasonality can be presented on a more interpretable and useful basis.
Appendix: Additional information on the approach to the seasonal adjustment of stocks and flows
Statistics Canada uses the X-12 ARIMA methodology to produce seasonally adjusted data. Time series are analyzed each year and the optimal specifications are selected. In some cases, a time series displays no evidence of seasonality and thus the seasonally adjusted and unadjusted series are one in the same. The FWA seasonal adjustment is done concurrently in that the seasonal adjustment incorporates the latest information for the time period in question in contrast with the use of fixed seasonal factors that are only periodically updated.
In cases where detailed series roll up into aggregates, such as more granular types of borrowing summing to total borrowing, two main approaches exist. One method is to seasonally adjust the details and roll them up into aggregates, which are checked for residual seasonality. Another approach is to seasonally adjust both the details and aggregates and use a raking procedure to ensure additivity is respected. For the sake of simplicity and clarity for users, the former method is employed and all resulting estimates are regularly verified to be free of residual seasonality.
Another optional constraint for X-12 ARIMA involves forcing annual totals of the flow variables to be equal for both the unadjusted and seasonally adjusted series. This ensures that the accumulation of flows over a calendar year will be identical and is useful in cases where annual benchmarks exist for certain flow series such as gross domestic product. A similar requirement can be imposed on stock estimates in that the unadjusted and seasonally adjusted levels at a given point in time (i.e., December 31) must be identical. For the FWA approach, forcing the annual totals is not strictly enforced to give priority to other constraints (see Table 1 which summarizes common characteristics of seasonally adjusted data in the context of the FWA approach).
| Characteristics | Current approach |
|---|---|
| Seasonality removed | Yes, no residual seasonality present in NBSA stocks or FFA and OCAA flows. |
| Annual total preserved | Non seasonal OCAA or FFA flows only; for seasonal OCAA or FFA flows, the unadjusted and seasonally adjusted total flows for the year do not exactly equal, but are not materially different. This was a necessary compromise to respect other constraints. |
| Seasonally adjusted series cuts through unadjusted series | Yes, in all cases |
| The flow-stock identify is respected for adjusted data (i.e., Lt = Lt-1 + Ft + OCAt) | Yes |
| Approach supports future expansion for other FWA series | Yes |
| Source: Statistics Canada, "Seasonal adjustment of stocks and flows in the Financial and Wealth Accounts: towards an integrated approach", Latest Developments in the Canadian Economic Accounts (13-605-X), 2018. | |
Finally, using year-over-year comparisons are frequently insufficient as the previous year’s quarter may contain seasonal bias compared with the current quarter. For example, moving holiday components (e.g., Easter) can have a significant effect on the level of each quarter. Year-over-year comparisons also tend to lack timeliness for the identification of turning points (recession or recovery) compared with quarter-to-quarter analysis of seasonally adjusted data.
The following sequence highlights each step of the current integrated FWA approach to seasonally adjusted stocks and flows.
Derivation of seasonally adjusted stocks, flows, and other changes in assets
Step 1. Seasonally adjust a stock version of the OCAA representing the cumulated flows
where,
and
Note: OCAA data are rarely seasonal, usually resulting in .
Step 2. Seasonally adjust the NBSA stock modified to exclude the OCAA stock
Note: the modified NBSA stock corresponds to a stock version of the FFA (cumulated FFA flows) with the same starting level as the (unmodified) NBSA stock.
Step 3. Derive the seasonally adjusted NBSA stock as the summation of the seasonally adjusted modified NBSA stock and the seasonally adjusted OCAA stock
Step 4. Derive the seasonally adjusted FFA and OCAA flows from their respective seasonally adjusted stock as the difference between the current and previous periods
where,
denotes series that are seasonally adjusted;
denotes series that are unadjusted for seasonality; and
denotes the seasonal adjustment process.
- Date modified:
