Testing for Provincial Industrial Structural Change through the 2000s

View the most recent version.

Archived Content

Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.

Archived

This page has been archived on the Web.

by W. Mark Brown

Skip to text

• Abstract
• Executive Summary
• 1 Introduction
• 2 Data and concepts
• 3 Changes in industrial structure, 2000 to 2010
• 4 Sensitivity analysis
• 5 Conclusion
• 6 Appendix

Text begins

Abstract

Using data from the provincial KLEMS database, this paper asks whether provincial economies have undergone structural change in their business sectors since 2000. It does so by applying a measure of industrial change (the dissimilarity index) using measures of output (real gross domestic product) and hours worked. The paper also develops a statistical methodology to test whether the shifts in the industrial composition of output and hours worked over the period are due to random year-over-year changes in industrial structure or long-term systematic change in the structure of provincial economies. The paper is designed to inform discussion and analysis of recent changes in industrial composition at the national level, notably, the decline in manufacturing output and the concomitant rise of resource industries, and the implications of this change for provincial economies.

Keywords: industrial restructuring; gross domestic product; hours worked; provincial economies.

Executive summary

After the early 2000s, the Canadian economy underwent considerable structural change, shifting away from manufacturing and toward resource-based industries and other sectors in reaction to rising commodity prices. This has created a demand for new data to assess these recent changes in provincial economies. This paper evaluates the size and nature of the changing industrial structure of provincial economies in the post-2000 period.
Using a new Statistics Canada database (Provincial KLEMS^Note1), this paper examines changes in industrial output (based on real gross domestic product [GDP]) and labour inputs (based on hours worked). Real GDP captures the extent of change in the provincial output of goods and services, excluding the effect of output prices. Hours worked measures the changing relative demand for labour across industries. Output and hours worked may not move in the same direction, as relative changes in industry productivity may decouple the two measures.

The provincial KLEMS data can be used to analyze the extent of change in Canadian provinces’ industrial composition since 2000. Across provinces, 6% to 12% of output and hours worked would have to be shifted across industries for the economy’s 2010 industry composition to match that of 2000. In other words, every year between 0.6% and 1.2%, on average, of output or hours worked was shifted across industries.

An assessment of whether these changes are structural, or the product of random, year-to-year movements requires statistical testing. The results in this paper show that the change in the industrial structure in most provinces was statistically significant, suggesting that provincial economies have been undergoing long-term structural changes. The specific industrial source of that restructuring depends on the province, although commonalities were apparent across provinces.

The most broad-based output gains were in retail trade: 9 out of 10 provinces had significant gains in the output share of this sector. Five provinces also had significant gains in construction and in administration and support services. For hours worked, there were consistent gains in administrative and support services, and losses in manufacturing and agriculture, forestry, fishing and hunting.

The share of output and hours worked in manufacturing fell more sharply in Ontario and Quebec than elsewhere, confirming the widely held view that manufacturing in these two provinces underwent substantial restructuring. Manufacturing output and hours worked declined in the other provinces, too, but the degree and statistical significance of the declines were less evident. Losses in manufacturing output in Ontario and Quebec were offset by significant gains in finance, construction, wholesale trade and retail trade.

Patterns of industrial restructuring in the remaining provinces were more idiosyncratic. Large output gains occurred in mining and oil and gas in Newfoundland and Labrador. Alberta experienced large output gains in finance and professional services. Both Saskatchewan and Alberta saw large gains in hours worked in construction, compared with other provinces.

1 Introduction

After the early 2000s, the Canadian economy underwent considerable structural change, shifting away from the manufacturing sector and toward resource-based industries partly reflecting rising commodity prices. This has created a demand for new data to assess these recent changes in provincial economies. The present analysis evaluates the size and nature of the changing industrial structure of provincial economies in the post-2000 period.

Using a new Statistics Canada database (provincial KLEMS^Note2), this paper examines changes in the industrial structure of provincial economies based on output (real gross domestic product [GDP]), and labour inputs (hours worked). Real GDP captures the extent of change in the provincial output of goods and services, exclusive of the effect of output prices. Hours worked measures changes in the relative demand for labour services across industries. Output and hours worked may not move in the same direction, as changes in industry productivity may decouple the two measures.

The statistical significance of these structural shifts is also tested. That is, the analysis examines statistically whether the changes observed in industrial structure can be attributed to persistent, long-term trends or to transitory, random shocks. This provides a firmer foundation to judge the evolution of provincial economies.

The organization of the paper is as follows. Section 2 describes the data sources and statistical techniques used in the assessment of structural change. Estimates of the intensity of structural change across provinces are reported and evaluated in Section 3. Section 4 tests the sensitivity of the statistical tests to differing assumptions. Section 5 concludes.

2 Data and concepts

2.1 Data source

The analysis is based on new public data, the provincial KLEMS database, published by the Canadian System of National Accounts. Released for the first time in January 2012, the provincial KLEMS data contain estimates of labour and capital inputs, gross output and value added, along with a range of productivity measures, available by province at the 2-digit level of the North American Industry Classification System (NAICS). These provincial data were developed to complement the national KLEMS database.

2.2 Measuring structural change

The analysis of structural change presented here focuses first on observed changes in the industrial distribution of real output, based on the contribution that individual sectors made to volume-based GDP in 2000 and in 2010. A measure of real GDP was selected because the objective is to evaluate actual changes in the volume of production, rather than changes in the relative value of that production, which depend on both the volume of outputs and the prices paid for those outputs (Baldwin and Macdonald 2009).

Level estimates of volume-based GDP that would readily allow for the estimation of industry shares are not available from the provincial KLEMS database. Estimates of these levels are derived by setting real GDP equivalent to nominal GDP in the base year (2002), and then using the indexed cumulative growth rates of real GDP, which are available from the database, to estimate the level of volume-based GDP before and after the base year (back from 2002 to 2000 and forward from 2003 to 2010). These volume-based industry-level estimates are converted into industry shares to facilitate the analysis.^Note3

There are, of course, conceptual and methodological challenges associated with the analysis of volume-based GDP in level terms. Not least of these is that GDP levels will depend on the base year selected. To assess the sensitivity of the results to the base year chosen, volume-based GDP shares were also evaluated using 2010 as the base year. This had no qualitative effect on the conclusions (Section 4).

The metric used to evaluate structural change is a standard dissimilarity index (D-index):

$$D=100\times {\displaystyle \sum _i\left|s_{it}-s_{it-\tau }\right|}/2,(1)$$

where $s_{it}$ is the industry share $i$ of volume-based GDP or hours worked in year $t$ (2010), and $s_{it-\tau }$ is the industry share in year $t-\tau$ (2000).^Note4 The D-index yields a scalar estimate of the degree of structural change that has occurred over this 10-year period, by indicating the percentage of provincial output that would have to be reallocated across industries in 2010 to return to the original distribution of output in 2000.

2.3 Structural change versus random changes

The focus of the paper is changes in industry structure that result from long-term shifts in demand and supply conditions. These changes need to be distinguished from shifts in industrial structure resulting from transitory, random shocks. For instance, on the supply side, temporary year-over-year changes in growing conditions can create large swings in agricultural output. When added across industries, these random shocks can result in an overall change in industry structure that is reflected in the D-index. Viewed in this way, the D-index could be interpreted as a measure of industry-level volatility, as opposed to one that quantifies the magnitude of structural change. It is important, therefore, to develop a methodology by which observed changes in industrial structure due to random shocks in industry output can be reasonably ruled out.^Note5 The remainder of this subsection constructs a statistical test to asses these changes at the provincial level.

At the industry level, the distinction between random shocks and long-term structural change can be placed within a standard hypothesis-testing framework:

• H0: The change in industry share over the period is due to the effect of random shocks.

• H1: The change in industry share is due to persistent processes.

The objective is to generate a set of random changes in industry shares against which observed changes can be compared.^Note6 This is analogous to the process of testing whether dice are loaded. In that exercise, a set of outcomes for the loaded dice are compared with the set of outcomes for unloaded dice. The primary problem in the present analysis is ‘unloading the dice’—developing a set of province-industry random shocks against which actual outcomes can be compared.

The random component for a given province-industry can be identified in the following manner. Recall that the D-index is given by:

$$D=100\times {\displaystyle \sum _i\left|s_{it}-s_{it-\tau }\right|}/2,(2)$$

where $s$ is the share of some measure of economic activity. For industry $i$, the change in share over the period is given by:

$$s_{it}-s_{it-\tau }={\displaystyle \sum _t{s}_{it}-s_{it-1}={\displaystyle \sum _t\Delta s_{it}}.} (3)$$

That is, the difference between end-points is simply the sum of the year-over-year differences in shares. This sum of differences can be divided conceptually into unknown systematic (structural) and random components:

$${\displaystyle \sum _t\Delta s_{it}}={\displaystyle \sum _t\left(\Delta {\phi }_i+\Delta {\epsilon }_{it}\right)}, (4)$$

where $\phi$ and $\epsilon$ are the systematic and random components, respectively, of the year-over-year change in share. Note that (4) is essentially a random walk time series model with a trend. Estimating the random component of (4) requires an estimate of the structural component (trend), which can bse accomplished via stochastic and deterministic means.

Using the stochastic approach, the structural component can be estimated via the mean difference of the share changes:

$$\Delta {\widehat{\phi }}_i=\frac{1}{\tau }\left({\displaystyle \sum _t\Delta s_{it}}\right), (5)$$

where it can be shown that $\widehat{\phi }$ is an unbiased estimator of $\phi$. The estimated random component is the observed year-over-year difference less the systematic component:

$$\begin{array}{l}\Delta {\widehat{\epsilon }}_{it}=\Delta s_{it}-\frac{1}{\tau }{\displaystyle \sum _t\Delta s_{it}},\text{ or}\text{(6)}\\ \Delta {\widehat{\epsilon }}_{it}=\Delta s_{it}-\overline{\Delta }{s}_i,\end{array}$$

where $\Delta {\widehat{\epsilon }}_{it}$ is an estimate of $\Delta {\epsilon }_{it}$. The random component is simply the demeaned difference, and has the same variance as the initial series of differences represented by (4). Hence,

$${\displaystyle \sum _t\Delta s_{it}}=\tau \overline{\Delta }{s}_i+{\displaystyle \sum _t\Delta {\widehat{\epsilon }}_{it}}, (7)$$

where ${\displaystyle \sum _t\Delta {\widehat{\epsilon }}_{it}}$ is zero.

Alternatively, the components of (4) can be estimated deterministically by regressing the share of industry $i$ in year $t$ on a linear trend:

$$s_{it}=\alpha +\widehat{\beta }trend+{\widehat{\widehat{\epsilon }}}_{it}.(8)$$

Therefore,

$$\Delta {\widehat{\widehat{\epsilon }}}_{it}=\widehat{\beta }-\Delta s_{it},(9)$$

where $\Delta {\widehat{\widehat{\epsilon }}}_{it}$ is an estimate of $\Delta {\epsilon }_{it}$ and $\widehat{\beta }$ is an estimate of $\Delta {\phi }_{it}$. Hence, equation (4) can be alternatively estimated by:

$${\displaystyle \sum _t\Delta s_{it}}=\tau \widehat{\beta }+{\displaystyle \sum _t\Delta {\widehat{\widehat{\epsilon }}}_{it}}. (10)$$

With the estimates of the random components in hand, the Monte Carlo simulation can be implemented at the province-industry level, and then, for the D-index itself.

At the province-industry level, a distribution of end-point industry shares is generated, where a set of 10 yearly changes in industry shares between $t-\tau$ and $t$ is randomly drawn (with replacement) from the 10-year, random industry level time series produced by equation (6) or equation (9). The set of random draws is then replicated 1,000 times. Each set of draws is added to produce a randomly generated share change for each industry for the 10-year period. The actual change in share is compared to this distribution in the form of a two-tailed test.

The intuition behind this test is simple. If an industry share has increased steadily year-over-year—an indication of a long-term shift in relative demand and/or supply conditions—the random component would be small relative to the systematic component. The cumulated growth of the 10 draws from the random set would be unlikely to match the actual change in industry shares over the period. On the other hand, if year-over-year changes in shares were large relative to expected year-over-year growth, it is likely that the actual change in share would not fall into the extreme tails of the random distribution; the null hypothesis could not be rejected.

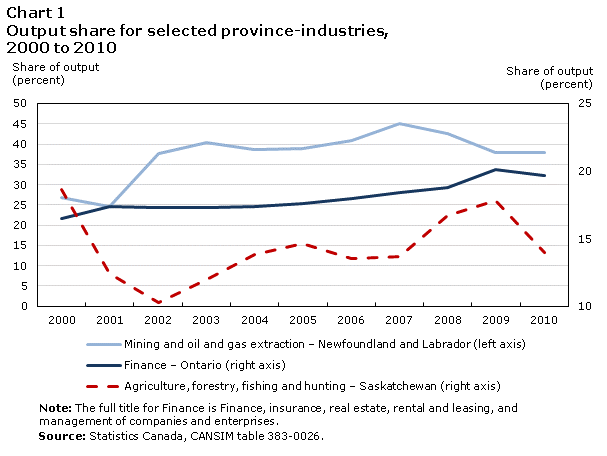
To illustrate the test, Chart 1 presents trends in industry output shares for selected province-industries: finance for Ontario; mining and oil and gas extraction for Newfoundland and Labrador; and agriculture, forestry, fishing and hunting for Saskatchewan.

For Ontario, the share of output attributable to finance^Note7 increased 3 percentage points, rising almost steadily through the period. For this series, the null hypothesis can be rejected at a 5% critical value.

By contrast, while the share of agriculture, forestry, fishing and hunting in Saskatchewan fell by 4.5 percentage points, the change was not statistically significant, reflecting considerable year-over-year variability in this series.

Finally, mining and oil and gas extraction in Newfoundland and Labrador increased its share of output by 11.1 percentage points, but the change in industry shares from 2000 was not statistically significant. Most of the gain occurred between 2001 and 2002. This break increased the overall variance of the series, which reduced the power of the test to identify a structural change.^Note8 However, it is difficult to argue that this was not a structural shift, as the increase in output share persisted after 2002. In this instance, it would be reasonable to conclude that the null hypothesis has not been rejected when it should have been (a Type 2 error). While this does not invalidate the statistical test, it suggests that the test cannot be applied mechanically without careful analysis of the underlying distributions generated by these data.

Description for Chart 1

For the D-index, the 1,000 randomly generated 10-year changes in industry share are used to calculate 1,000 D-indices for each province. Their distribution is used to determine whether the null hypothesis (the index is generated through a transitory, random process) can be rejected for a given critical value using a one-tailed test. A one-tailed test is used because the expected value of the index under the null hypothesis is zero or greater, because the expectation is taken on the absolute value of the random component:

$$H0:E\left(D\right)=\frac{1}{2}E\left({\displaystyle \sum _i\left|{\displaystyle \sum _t\Delta {\epsilon }_{it}}\right|}\right)\ge 0.(11)$$

In related work, Cortese, Falk and Cohen (1976) developed a theoretical distribution for the D-index under the assumption of randomness for instances when the D-index is measured in cross-section (for example, measuring residential segregation across visible minority groups). Leckie et al. (2012) also developed a test for the D-index based on a binomial sampling distribution and extended it within a multi-level modelling framework.

The present analysis takes advantage of the time-series nature of the data to develop a set of Monte Carlo simulations that are simple to calculate and do not require distributional assumptions per se. This is appropriate for these data, because it is unclear what underlying random process is driving shifts in industry structure through time.

The following discussion focuses on Monte Carlo simulation results based on the stochastic random component estimates. To test the sensitively of the results to the estimator chosen, reference will also be made to results derived from the deterministic random component.

3 Changes in industrial structure, 2000 to 2010

3.1 Share of gross domestic product

The D-index ranged from 5.9 in New Brunswick to 12.2 in Newfoundland and Labrador. That is, between 5.9% and 12.2% of GDP would have to be reallocated across industries for the 2010 provincial industrial structure to match that of 2000 (Table 1). Thus, for any given province, between 0.6% and 1.2% of GDP per annum is being reallocated across industries.

At issue is whether these changes are statistically significant. For New Brunswick, Newfoundland and Labrador, Prince Edward Island, and Saskatchewan, the null hypothesis that these shifts in industrial structure were random could not be rejected. Newfoundland and Labrador, however, is a special case and will be discussed in more detail below. For the remaining six provinces, there is statistical support of a structural shift in their economies (Table 1).

Across the provinces, the most consistent and statistically significant gains by industry were in retail; only Newfoundland and Labrador did not experience a significant gain here. Gains in output share were also widespread in construction, finance, and administrative and support services.^Note9

The most consistent and statistically significant losses were in manufacturing. These losses were concentrated in Ontario and Quebec, where the share of output accounted for by manufacturing dropped by 9.5 and 8.3 percentage points, respectively. No sector in any other province experienced such large losses.

Other notable shifts in industrial structure were apparent. As mentioned above, in Newfoundland and Labrador, mining and oil and gas extraction increased its share of GDP from 26.9% to 38.0% (11.1 percentage points), as additional offshore oil and gas production came online. Much of the overall change in industrial structure measured by the D-index is driven by this sector. Neither the change in the D-index nor the change in this industry’s share of output is statistically significant, because of the large jump in output between 2001 and 2002 (Chart 1). Nevertheless, this is a persistent, meaningful change in the structure of the Newfoundland and Labrador economy.

Nova Scotia experienced extensive change in industrial structure. Retail trade, professional and scientific services, and administrative and support industries experienced significant gains (Table 1). Prince Edward Island and New Brunswick did not see any broad-based shifts in their industrial structures.

As noted above, in Quebec and Ontario, the manufacturing share of output declined: from 30.3% to 22.0% in Quebec, and from 29.8% to 20.3% in Ontario. Both provinces saw significant gains in construction, retail trade, and finance. In Ontario, the finance sector experienced the largest increase in output share of all the provinces, rising by 3.2 percentage points from 16.5% to 19.7%. In 2000, output in finance was just over half that of manufacturing, but by 2010, they were about equal.

Both Manitoba and Saskatchewan saw significant output gains in construction and retail trade. Outside of these sectors, no statistically significant shifts in industrial structure occurred in either province.

Broad-based shifts occurred in Alberta’s industrial structure. The largest loss in output share was in mining and oil and gas extraction, which fell 5.8 percentage points from 29.4% to 23.6%. This did not result from a decline in the volume of output, which, in fact, increased. Rather, relatively large output gains in other industries reduced this sector’s share. Six sectors saw significant gains, including finance, retail trade, and professional, scientific and technical services. This reflects the lag between investment—which helps to drive growth elsewhere in the Alberta economy—and the production of unconventional oil.

British Columbia experienced a significant decline in the output share of manufacturing. It was also the only province with a significant fall in the share of output in the agriculture, forestry, fishing and hunting sector. The most significant gains were in construction and retail trade, with smaller gains in professional, scientific and technical services and administration and support. It is notable that, in 2010, finance had eclipsed manufacturing as the most important sector (Appendix, Table 5).

3.2 Share of hours worked

Shifts in the composition of provincial output may influence demand for labour, measured here by hours worked. However, the demand for labour will not necessarily mirror changes in output. For instance, industries gaining output share may not see similar gains in hours worked if the output gains coincide with rising labour productivity. Similarly, industries with little or no loss of share in output may experience significant relative declines in hours worked if they are substituting capital for labour.

This dynamic is apparent in agriculture, forestry, fishing and hunting. In most provinces, output in this sector was in relative decline, but only in British Columbia was this change statistically significant (Table 1). However, in most provinces, the share of hours worked in agriculture, forestry, fishing and hunting fell significantly, and in all instances, more than did output (Table 2). For instance, the share of hours worked in this sector fell by 8.9 percentage points (from 21.5% to 12.6%) in Saskatchewan while its output share fell by 4.6 percentage points (from 18.6% to 14.0%). Underlying this difference is the high rate of labour productivity growth in agriculture, forestry, fishing and hunting in Saskatchewan—an increase of 49% between 2000 and 2010.

Differences between trends in output and hours worked can be seen elsewhere. The share of hours worked in retail trade did not rise significantly in any province, whereas the retail trade share of output rose significantly in all provinces except Newfoundland and Labrador.^Note10 The same was true of finance; only in Nova Scotia and Quebec did the share of hours worked in finance increase significantly.^Note11 By contrast, the share of hours worked in construction rose more than did construction’s share of output. This was most evident in Alberta where the share of output in construction increased by an insignificant 0.2 percentage points, while the share of hours worked rose by 4.4 percentage points from 12.7% to 17.1%, reflecting a 21% decline in relative labour productivity over the period.

After agriculture, forestry, fishing and hunting, it is in manufacturing where the share of hours worked fell the most. While the majority of provinces experienced significant declines, the decreases were most pronounced in Quebec and Ontario. In Quebec, the share of hours worked in manufacturing dropped by 7.0 percentage points from 23.4% to 16.3%, and in Ontario, by 6.2 percentage points from 20.9% to 14.7%.

Across the provinces, the magnitude of the overall change in industrial structure measured by hours worked is similar to changes measured by output, although differences emerge on a province-by-province basis. When hours worked is used as a metric, more structural change is apparent in some provinces, and less structural change is apparent in others. Nonetheless, most saw a statistically significant change. The exceptions are Newfoundland and Labrador, Prince Edward Island and Manitoba. In fact, when both metrics of structural change are considered, it is only Prince Edward Island for which the null hypothesis of no change cannot be rejected without question.

4 Sensitivity analysis

The results to this point may be sensitive to assumptions chosen. These include the estimator used (stochastic versus deterministic), the presence of extreme observations, and in the case of volume-based GDP, the base year chosen. It is, therefore, important to assess the robustness of the statistical tests to these potential problems.

Table 3 presents D-index significance tests calculated using several methods for provincial volume-based GDP.^Note12 The first set of sensitivity tests is based on random error terms derived from the stochastic methods. For convenience, the first column presents the significance levels for the D-index in Table 1. As noted above, the outcome of the statistical test may be influenced by large breaks in the time series. To address this issue, the random components derived from extreme year-over-year changes were excluded from the Monte Carlo estimation.^Note13 This had little effect on the level of significance, except for Manitoba whose D-index became significant at the 10% level. Changing the base-year from 2002 to 2010 has little influence on the results.

In almost all instances, the deterministic tests yield the same significance levels as the stochastic-based tests, so there is really little to choose between them.

For hours worked, the significance tests on the D-index also proved not to be sensitive to differing methods (Table 4). Excluding extreme observations from the Monte Carlo simulation had no effect on the results. Furthermore, across the stochastic and deterministic tests, there was no qualitative change in the results, and no indication that one test was more efficient than the other.

The deterministic and stochastic tests were also compared at the industry level (Appendix Tables 7 and 8). These tests will differ systematically if one estimator is more efficient than the other. However, despite variability across province-industries in terms of statistical significance, no systematic difference between the tests emerged.

5 Conclusions

The provincial KLEMS data can be used to demonstrate the extent to which Canadian provinces have experienced statistically significant changes in their industrial composition in the post-2000 period. Across provinces, 6% to 12% of output and hours worked would have to be shifted across industries for their 2010 industrial composition to match that of 2000. In other words, every year between 0.6% and 1.2% on average of output or hours worked was shifted across industries. An assessment of whether these changes are structural, and not temporary, requires statistical testing. The analysis shows that, for most provinces, the change in industrial structure was statistically significant. The evidence indicates that provincial economies have been undergoing long-term structural change. The specific industrial source of that restructuring depends on the province, but commonalities were apparent across provinces.

The most broad-based output gains were in retail trade—9 out of 10 provinces saw significant structural gains in the output share of this sector. Five provinces also saw significant structural gains in construction and administration and support services. For hours worked, there were gains in administrative and support services, and losses in manufacturing and agriculture, forestry, fishing and hunting.

In Ontario and Quebec, the share of output and hours worked in manufacturing fell more than elsewhere, thereby confirming the widely held view that manufacturing in these provinces underwent substantial restructuring since 2000. The shares of output and hours worked attributable to manufacturing declined in the other provinces as well, but the degree and statistical significance of these declines were less evident. Losses in manufacturing output in Ontario and Quebec were offset by significant structural gains in finance, construction, wholesale trade and retail trade.

Patterns of industrial restructuring in the remaining provinces were more idiosyncratic. Large structural output gains in mining and oil and gas occurred in Newfoundland and Labrador. Alberta experienced large output gains in finance and professional services. Both Saskatchewan and Alberta saw large gains in hours worked in construction.

6 Appendix

6.1 Data description

6.2    Sensitivity of results to estimation method

 

---

Notes

1. KLEMS refers to Capital, Labour, Energy, Materials and Services.
2. KLEMS refers to Capital, Labour, Energy, Materials and Services. For background on national KLEMS data, see Baldwin, Gu and Yan (2007).
3. Industry shares are derived from provincial totals that are the sum of province-industries. Due to the non-additivity of Fisher-based industry volume estimates, this summation may differ from Fisher-based volume estimates that start from province-level GDP.
4. See Duncan and Duncan (1955) for an early discussion of the D-index as a measure of segregation.
5. This is a widely recognized problem in the segregation literature (Leckie et al., 2012).
6. Cortese, Falk and Cohen (1976) develop a theoretical distribution for the D-index under the assumption of randomness for the case when the D-index is measured in cross-section (for example, when measuring residential segregation across visible minority groups).
7. The full title of the sector is: Finance, insurance, real estate, rental and leasing and management of companies and enterprises.
8. If the share change between 2001 and 2002 is substituted with a randomly drawn share change from other years in the Monte Carlo simulation, the change in share for mining and oil and gas extraction in Newfoundland and Labrador is statistically significant.
9. The full title of the sector is Administrative and support, waste management and remediation services.
10. See Baldwin and Lafrance (2013) for a more in-depth analysis of output and productivity in the retail sector.
11. This was consistent with reports of a growing financial sector in Nova Scotia (Greater Halifax Partnership 2007).
12. Across the methods employed, the Monte Carlo simulations are based on the same set of randomly generated numbers, so variation in the results cannot be attributed to different draws of a randomly generated set.
13. Industries with potentially large year-over-year changes in share were defined as those where the share change between 2000 and 2010 was greater than 10% in absolute terms, and the skewness (3rd moment) of the distribution of yearly share changes was greater than 1.5. If this holds for an industry, the estimated random component associated with the yearly change in share with the largest absolute value is replaced with a random draw from the remaining nine random components.