Acknowledgements
The authors thank Robby Bemrose for his assistance in building the firm networks database and Steven Brakman for comments on an earlier version of this paper. The authors also acknowledge the financial support of Innovation, Science and Economic Development Canada, which supported both the development of the estimates of inter-regional trade and the estimation of the effects of firm networks on trade.
Abstract
While the presence of provincial border effects—the relative weakness of inter-provincial trade compared to intra-provincial trade—is well established, it remains unclear what underlies them. Parsing out the sources of the border effect is important, because it provides policy makers with much more information on where to direct their efforts. This paper takes a step in this direction by asking whether part of the border effect can be attributed to how multi-unit firms organize their production within and across provincial borders. Networks of operating units controlled by the same enterprise lower the cost of trade by shipping goods between units as value is added through the production chain or via the use of common upstream and downstream supply chains. Higher costs of operating these networks in multiple provinces may act as a barrier to firm networks. By combining measures of regional trade and firm networks over a nine-year period (2004 to 2012), the study tests these propositions. It finds that, while many firms operate networks across multiple provinces, firm networks dissipate with provincial borders, and that this has important implications for trade. Using a gravity model, the study finds that provincial border effects fall by about half after accounting for firm networks. This results both from provincial borders acting as a barrier to firm networks and from networks that cross provincial borders acting less as a complement to, than a substitute for, trade.
Executive summary
While the presence of provincial border effects—the relative weakness of inter-provincial trade compared to intra-provincial trade—is well established, it remains unclear what underlies them. Parsing out the sources of the border effect is important, because it provides policy makers with much more information on where to direct their efforts. This paper takes a step in this direction by asking whether part of the border effect can be attributed to how multi-unit firms organize their production within and across provincial borders. Networks of operating units controlled by the same enterprise lower the cost of trade by shipping goods between units as value is added through the production chain or via the use of common upstream and downstream supply chains. Higher costs of operating these networks in multiple provinces may act as a barrier to firm networks that facilitate trade. This may transform the complementary effect of firm networks on trade into a trade substitution effect. In combination—a weaker presence across provincial borders and border-cost-induced trade substitution effects—may help to explain the strength of provincial border effects.
This paper investigates the effect of firm networks on border effects by combining measures of regional trade and firm networks over a nine-year period (2004 to 2012). In particular, it asks the following questions:
- Are distance and provincial borders associated with the extension of firm networks of operating units across regions?
Firm network ties decline with distance. This is consistent with firms incurring costs of organizing their production across longer distances. Firm network ties also fall across provincial borders. After taking distance into account, the study finds that firm network ties are about 19% weaker across provincial borders than within them.
- Do firm networks act as a complement or substitute for trade across regions?
With rising distance and the presence of provincial borders, the complementary effect of firm networks on trade falls. As well, at sufficiently long distances and when crossing borders, networks switch from being a complement to being a substitute for trade. That is, when trade occurs over 1,200 km and crosses a provincial border, the effect of firm networks on trade turns from that of a complement to that of a substitute. For many important provincial trading relationships (e.g., Alberta–Ontario), the effect of firm network on trade is negative.
- To what extent do firm networks account for provincial border effects?
All else being held equal, trade across provincial borders is about 60% of intra-provincial trade. However, when the strength of firm network ties is taken into account, this proportion rises to 80%.
1 Introduction
Trade costs have proven to have a significant effect on the degree of economic integration between regions and countries (Anderson and van Wincoop 2004; Chaney 2008; Behrens and Brown 2018). Although the magnitude of these costs can be estimated relatively easily, their sources are much more difficult to discern. Furthermore, while in Canada transport costs make a significant contribution to overall trade costs (Behrens and Brown 2018),Note 1 the strong presence of provincial border effects suggests that other factors that have yet to be taken into account are at play (Bemrose, Brown, and Tweedle 2017). Unlike in the United States, where refined data and methods have reduced estimates of state-level border effects to zero (Hillberry and Hummels 2008), in Canada there is still evidence that provincial borders matter (Agnosteva, Anderson, and Yotov 2014; Albrecht and Tombe 2016), measuring approximately 6.9% in tariff equivalent terms (Bemrose, Brown, and Tweedle 2017). The obvious next question is: “What trade costs lie behind these border effects?” or, perhaps more accurately in this instance, “Do borders and the costs to firms that they entail intervene to reduce the ability of firms to mitigate trade costs?”
Among the more important trade costs are those that firms incur when engaging in market transactions (Williamson 1979) that, in turn, influence the patterns of trade (Rauch 1999). In order to minimize these costs, it is sometimes advantageous for the boundaries of the firm to extend across borders. As firms expand into new areas, trade may be induced as they engage in lower-cost, intra-firm trade and/or extend their existing supply chain. Regarding the former, it bears noting that about one-third of world trade occurs within firms (Antràs 2003; Antràs and Helpman 2004). Regarding the latter, there is evidence that firms that are taken over subsequently adjust their production technologies, including downstream shipment destinations and likely their upstream supply chains, to more closely match those of the acquiring firm (Atalay, Hortaçsu, and Syverson 2014).
While the role of intra-firm trade on the international stage is well known, relatively little is known of the role of intra-firm trade at the subnational level (Anderson 2011; Atalay, Hortaçsu, and Syverson 2014), or, more broadly, the effect of firm networks on trade. In particular, one factor that underlies the integration of provincial economies through goods trade may be important: intra-firm linkages that extend across provincial borders, or a lack thereof (Helliwell 1998). Hence, this paper investigates the nature of firm networks in Canada, their relationship with regional goods trade, and how much they account for the effect of provincial borders on trade flows. In particular, the analysis addresses the following questions:
- To what extent is a provincial economy knit together by multi-location firms (firm networks)?
- How easily do these firm networks spill across provincial borders? That is, as with trade, firm networks (i.e., operating locations controlled by the same firm) may be more prevalent within provincial borders as firms may incur extra costs when entering new provincial markets (e.g., adapting to a new set of regulations). Alternatively, they may be more prevalent when market access (e.g., eligibility to bid on government contracts) depends on demonstrating a physical presence in the province (Chaundy 2016).
- How much do these firm networks influence provincial integration through goods trade? Specifically, how much do firm networks account for provincial border effects? Do firm networks enhance trade by reducing transaction costs, or do they reduce trade by allowing firms to save on trade costs by producing goods in local markets?
To address these questions, the study looks at information on both goods trade and firm networks across regions. Trade is measured using Statistics Canada’s newly created Surface Transportation File (STF), which builds up from a set of geo-coded, transaction-level records to form a coherent set of estimates of the value of trade across regions. Firm networks are measured using the Business Register (BR), which contains information on both the structure of firms (i.e., firms and the operating units they control [i.e., manufacturing plants]) and the location of operating units. Using a common geography, these two data sets can be combined to provide a measure of both trading links between regions and firm-based links. Furthermore, both files cover a 9-year period (2004 to 2012), providing measures of firm networks and trade through time using a geographically consistent panel of regions. While the study period ends in 2012, the value of the analysis rests on revealing the underlying relationship between firm networks, trade and provincial border effects that are unlikely to shift through time.
This work contributes to two broad areas of research: borders and barriers to trade; and firm networks.
1.1 Borders and barriers to trade
Accounting for firm networks may help to parse the provincial border effect. Generic barriers to trade have been explored in several studies, and can be substantial (for an overview, see Anderson and van Wincoop 2004). Quite naturally, firms seek to minimize these costs. Multinationals, for example, may use affiliate ownership to reduce trade costs associated with contract enforcement problems (Yeaple 2013). In this view, firms with vertically integrated supply chains expand and engage in intra-firm trade to minimize such costs; this leads to the complementarity of investment and trade. However, recent research has shown that this intra-firm trade is not always part of a supply chain, even when the affiliate is in an industry that is upstream of the domestic firm (Ramondo, Rappoport, and Ruhl 2016), a result that seems to also apply to domestic vertically integrated firms (Atalay, Hortaçsu, and Syverson 2014). The implication of this stream of literature is that the impact of firm networks on trade may be less than originally thought.
Still, the relationship between firm networks and trade may go beyond this more limited view. Information asymmetries, for example, in the form of firm contacts in different trading destinations, have been used to explain the pattern of international trade (Chaney 2014). Firm ownership is a way in which a firm can increase local knowledge of destinations, reducing these informational asymmetries, thereby inducing trade between regions. Furthermore, if firms maintain their network of upstream suppliers—i.e., their supply chain—as they extend their network of operating locations outwards, trade may be induced. Hence, whether through mitigating the costs of intra-firm transactions, reducing informational asymmetries, or extending supply chains, the expansion of firm networks may be complementary to trade.
On the other hand, firms may also use their local affiliates to circumvent trade barriers. They may do so to overcome transport costs, to tailor their products and services to local needs (e.g., to account for regulatory differences), and/or to meet local content requirements for some government contracts (Chaundy 2016). From this perspective, trade and investment may be substitutes. If the primary influence of firm networks on trade is complementary, these networks may help to account for provincial border effects in cases where firms are less likely to extend their operations across provincial borders. The opposite holds true, of course, if they are substitutes.
This paper contributes to the study of trade barriers by investigating the association of firm networks with barriers to provincial trade in Canada. It is closely related to the literature that relates business and social networks of immigrants to aggregate trade, starting with Rauch (1999, 2001). The idea is that immigrants make connections between their contacts in the new and home countries and that the countries trade more than they otherwise would without these connections. The focus of the study is, however, on the specific channel of a firm owning operating locations in different regions and on the aggregate effect of those connections on regional trade. In this regard, this work has much in common with Combes, Lafourcade, and Mayer (2005), who found that both firm networks and migration reduced measured intra-national barriers to trade, and Garmendia et al. (2012), who examined the effect of networks and migration and found that both reduced Spanish provincial border effects, with firm networks being more important. This paper, however, pushes beyond the work of Combes, Lafourcade, and Mayer (2005) and Garmendia et al. (2012) by using panel methods to control for endogeneity and to address questions of complementarity and substitutability between investment and regional goods trade.
1.2 Firm networks
A large body of literature has examined firm networks, their characteristics, and impacts on productivity and trade. In this case, spatial characteristics are the object of interest, but this work also connects to these broader lines of research.
In descriptive terms, Atalay et al. (2011) showed the prevalence of firm networks and their relationships to firm size (in customer–supplier relationship terms), and Lim (2017) showed the impact of fixed costs on establishing firm–firm relationships. One important result is that reducing trade costs within the supply chain has been shown to increase firm productivity in Japanese firm networks (Bernard, Moxnes, and Saito 2015), supplementing previous work on Japanese keiretsus (Belderbos and Sleuwaegen 1996, 1998; Head, Ries, and Spencer 2004). These findings suggest provincial barriers that impede the establishment of firm networks and, ultimately, savings on trade costs may have an impact on productivity.
Drawing from this, the study also takes a step back to look at the networks themselves, specifically at how distance and borders matter there, too. This is crucial because, for firm networks to matter for trade across borders, they also need to be less prevalent across borders. The existing literature does not address this, and therein lies an additional contribution. This relates to work on a multinational enterprise’s (MNE) choice to open a new foreign affiliate (greenfield investment) or take control of an existing location (i.e., through mergers and acquisitions [M&A]). The fact that M&A is the dominant form of foreign direct investment suggests an MNE uses acquisition to partially overcome regulatory and informational barriers that the border introduces (Nocke and Yeaple 2007), since it must be easier to satisfy local regulations by acquiring something that already exists and already satisfies those regulations.
The remainder of this paper is organized as follows. Section 2 draws from the theoretical and empirical literature on multinationals to develop a set of hypotheses regarding the extension of firm networks across space and borders and the relationship between firm networks and trade. Section 3 describes the data sources and methods used to measure firm networks. Section 4 provides a description of provincial firm networks and an econometric analysis of the factors affecting firm networks at the provincial level and finer geographies. Section 5 presents the impact of firm networks on trade. It is followed by the Conclusion (Section 6) and the Appendix.
2 Multiunit firms and trade
To put this paper into context, it is necessary to return to the fundamental reasons why firms choose to operate multiple units and why sometimes it is advantageous to locate units across borders, be they national or subnational, and to examine what this suggests regarding inter-regional trade. It is helpful to address these questions with their implied hypotheses in sequence, rather than all at once.
2.1 Why do firms have multiple units?
There are three types of multiunitNote 2 enterprises (Caves 1996): (1) horizontal (units produce the same goods / service), (2) vertical (units are related functionally through upstream–downstream links), and (3) diversified (units are neither horizontally nor vertically related; investments can be viewed as portfolio diversification strategy). The focus here is on horizontally and vertically linked firms. Firms organize themselves horizontally to internalize the market for proprietary assets, while those that organize themselves vertically internalize markets for intermediates. Vertically linked firms, however, do not necessarily need to trade internally as
“...[t]here can be transaction-cost economies in the procurement of raw materials that go beyond the input needs of a single plant’s output. Economies can arise in the transportation network for outbound shipments of finished goods that extend beyond the single plant’s output.” (Caves 1996, p. 6)
This is consistent with evidence on domestic (Atalay, Hortaçsu, and Syverson 2014) and international (Ramondo, Rappoport, and Ruhl 2016) intra-firm trade patterns. Furthermore, the economies gained by developing a horizontally or vertically linked structure have to be traded off against the costs of managing these operations. As those costs rise, firms are likely to engage in more arm’s-length transactions. One dimension along which one would expect (Duranton and Puga 2005) and find (Behrens and Sharunova 2015; Baldwin and Brown 2005) evidence of rising management costs is the distance between units. For instance, operating units of a multiunit firm are more geographically compact than a randomly drawn set of single-unit firms in the same industry (Behrens and Sharunova 2015). The implication, of course, is that, as the distance between probable units increases, the benefits of internalizing markets for proprietary assets are more likely to be outweighed by the cost of managing far-flung operations. This leads to the study’s first hypothesis.
Hypothesis 1 (H1): Facing a trade-off between economies gained from operating multiunit enterprises and the cost of managing these operations, the prevalence of firm network ties will fall with distance between regions.
2.2 When do firms expand across borders?
When crossing borders, the entrepreneur incurs the additional fixed costs of learning how to operate in a different jurisdiction, be it a country or province in this instance.
“The typical entrepreneur, a native of some particular country, brings to his or her business activities a general knowledge of its legal and social system and its peculiar ‘way of doing things’.” (Caves 1996, p. 57–58)
The transaction cost advantage of the multiunit firm is required in order to counterbalance these costs. The same principles apply to national markets. “Indeed, the early process of expansion of firms to national-market status in the nineteenth-century U.S. economy was apparently quite similar to their evolution to multinational status more recently.” (Kindleberger 1969, p. 33–35) This trade-off informs the second hypothesis.
Hypothesis 2 (H2): Firms are less likely to establish firm networks across provincial borders, as a result of the higher cost of operating in multiple provinces.
The opposite relationship could hold if government procurement rules stipulated that firms must have a physical presence in a province in order to qualify for contracts (Chaundy 2016). It is unlikely this specific form of contracting rule would determine the overall pattern of investment. Therefore H2 is maintained as the primary hypothesis.
2.3 How do firm networks influence trade?
There are two relevant perspectives. The first is a basic model of trade and investment that can be applied to show that rising trade costs (e.g., tariffs or transportation costs) will result in declining exports corresponding to rising local production. Hence, rising trade costs shift the effect of firm networks from being a complement to trade to being a substitute for it. This linear relationship holds with decreasing returns to scale, but not with increasing returns, where production is either at home or abroad. Brainard (1997) showed that sales of subsidiaries of U.S. MNEs (as a proportion of those sales plus U.S. exports) increased with transportation costs. The broader conclusion is that, the higher the trade costs, the larger the proportion of MNEs’ sales in the host country that is accounted for by local production. The following hypothesis draws on this point.
Hypothesis 3 (H3): Higher trade costs—associated with distance or borders—for a given firm switch the effect of firm networks on trade from positive to negative (from complement to substitute).
The second perspective is more subtle but could be as, or more, important. In accordance with the Transaction Cost Economics (TCE) framework, firms will organize themselves in order to minimize “...costs of production and associated logistical activities of the firm” (Caves 1996, p. 2, emphasis added). One of the firm-specific assets that contribute to firms expanding their operations horizontally or vertically is their logistics capabilities as expressed via their supply chain. For retail and wholesale enterprises, their ability to build and manage their supply chains is likely one of their more important assets. The TCE perspective suggests that, even when there are no ownership ties, the need for some form of contractual arrangement means the switch between suppliers has a cost (Williamson 2008). In fact, Atalay, Hortaçsu, and Syverson (2014) found that, after a unit is purchased, its production technology and shipment destinations looks increasingly like the acquiring firm’s. Hence, firms—regardless of their horizontal or vertical structures—will tend to maintain their supply chains.Note 3 As firms expand into new areas (or contract), so too do their supply chains. As a result, even when there is no input–output relationship between the units, trade between regions may rise, simply because firms have an established network of suppliers that moves with them. However, once again, maintaining these networks across space has a cost, and over longer distances it is less likely they will be maintained as the additional transportation costs outweigh the lower costs of utilizing an existing network of suppliers. This leads to the fourth and final hypothesis.
Hypothesis 4 (H4): The effect of firm networks on trade will decline with distance as the cost of maintaining supply chains outweighs their benefits.
Of course, H3 and H4 are observationally equivalent. Hence, it will not be possible to distinguish between the two processes. It will, however, be possible to establish whether trading relationships over space are consistent with both.
3 Methods
The analysis is based on the measurement of firm networks and trade across regions. The former requires detailed information on the structure of firms and their locations, while the latter requires information on goods trade across a similar geography. Each of these data sources is described in sequence below, beginning with firm networks.
3.1 Defining and measuring firm networks
The study seeks to measure the degree to which regions are linked via firm
networks and the association between these networks and trade flows. Firm
networks by their very nature are composed of multiunit firms, or what will be referred
to here as “multi-location firms” in order to be consistent with naming
conventions of the BR. Two geographic regions are linked if operating locations
in each are part of the same (multi-location) firm. For instance, Toronto and
Halifax are linked through a firm network if a supermarket chain has operating
locations in both. A simple way to measure firm networks between two regions is
to count the number of operating locations in a geographical unit that are part
of the same multiunit firm operating in both.Note 4
Figure 1 illustrates this conceptually.
Firm has one location in region and two locations in region , while firm has two locations in each of region and region . Hence, from the perspective of region , the number of locations linked to is 3, while the number of
locations in region linked to is 4. Note that
multi-location firm has a location in , but none in , and so its locations are not counted when considering locations in linked to . In formal terms, the strength of firm network () connections from region to region over each firm is calculated as follows:
where
is the count of operating locations of firm in region . As is apparent from this
equation and the example described above, firm links are bidirectional but
asymmetric.
Equation (1) is useful in the analysis of
firm networks between geographic regions for two reasons. First, it can be
derived from a reduced form model, the details of which are presented in Subsection 4.1.
Second, it provides the foundations for the analysis to the relationship
between firm networks and trade flows that requires networks to be measured in
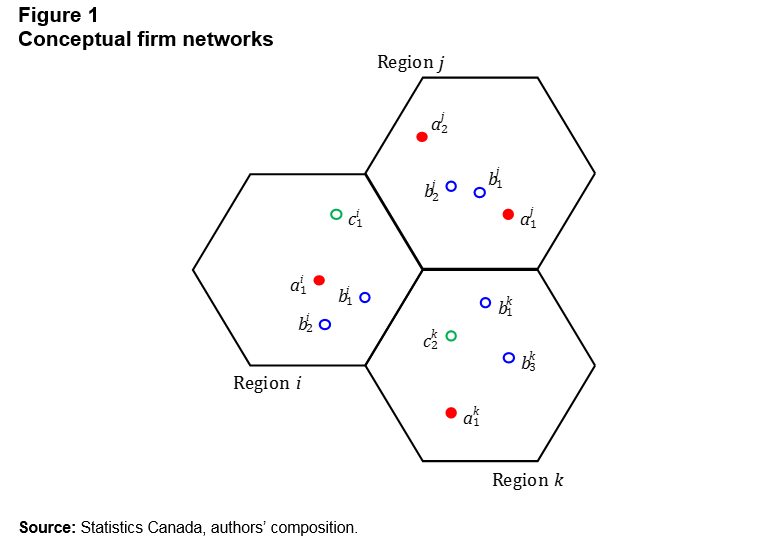
Description for Figure 1
The title of Figure 1 is “Conceptual firm networks.”
The diagram depicts possible locations of different firms in different regions.
There are three regions, represented as hexagons, labeled Region , Region and Region .
The hexagons are contiguous (they are joined on two sides) and are delineated by a black line.
In Region : firm
has one location (); firm has two locations (, ); and firm has one location () .
In Region : firm has two locations (, ); firm has two locations (, ); and firm has zero locations.
In Region : firm has one location (); firm has two locations (, ); and firm has one location ().
The source of this diagram is "Statistics Canada, authors' composition."
a slightly different way. According to Equation (1), trade would be
a function of whether there was a firm network present and weighting on the
size of the firm as measured by the number of its operating locations in . On a pairwise basis, however, the effect of networks on trade
depends on the firm’s locations in both regions. One simple way of capturing
the bilateral firm links of regions and is to take into account the
asymmetry implied by Equation (1) to capture the to links as well:
The aggregate additive measure thus represents total links
between and , where is a mnemonic for “additive.”
This additive measure likely captures whether firms have built knowledge of
markets in both regions, but it may not fully take into account the potential
for intra-firm trade, because the size and industries to which the locations
belong are not taken into account.
Other methods can be used to measure firm
networks. The study evaluates several different specifications, including
reframing the problem in terms of a typical mathematical definition of a
network (a set of nodes and edges), and tests different ways to weigh the links
to account for the number of firm locations and firm size that can characterize
the potential for trade. The results for these specifications are similar;
these formulations and results are presented in the Appendix.
3.2 Data
These measures of firm networks require a
method to identify multiunit firms over subnational geographies. Statistics
Canada’s Business Register (BR) is an inventory containing all businesses in Canada,
where firms are defined as multiunit if they have more than one operating
location. For example, a manufacturing firm is considered to be multiunit if it
has more than one plant (operating location). Measuring firm networks from the
BR is possible since it provides information on a firm’s operating structure,
geographical location, and industry (six-digit level of the North American
Industry Classification System). By using the geographical and industry
information also available, it is then possible to assess whether such a firm
has operating locations within and across geographic units, by industry.
Over time, the BR has undergone changes
that have improved the statistical coverage of businesses in Canada.
Analytically, however, this is a challenge, because such changes to the frame
of businesses may compromise the BR’s longitudinal consistency. For example,
the inclusion of additional detailed tax data (T4 tax filings)
in the BR in 2009 improved the coverage of multi-province firms. However, this
results in many longitudinally inconsistent births of locations belonging to
multiunit firms between 2008 and 2009. To improve the longitudinal consistency
of the file, indicators available on the BR were used to exclude firms affected
by such changes to the BR frame. The 2004-to-2012 time period is used to match
the time period covered by the STF that is used to measure regional trade flows.
3.2.1 Sectoral breakdown
The study focuses on the business sector and provides a sector breakdown,
defined as follows. A multiunit firm is said to be in the goods sector if every
one of its operating locations is goods-producing. Similarly, a multiunit firm
is in the services sector if all of its operating locations are in the services
sector. Multiunit firms that have both goods- and services-producing operating
locations are said to be in the hybrid goods sector, since they are linked to
both the goods and the services sectors. Note that the hybrid goods sector
contains only locations belonging to multiunit firms by definition. On average
over the 2004-to-2012 period, services-only comprised almost 75% of business
sector operating locations. This is compared to 23.2% of operating locations in
the goods-only sector and 2.2% of operating locations in the hybrid goods
sector (see Table 1).
Table 1
Business sector breakdown, operating locations
Table summary
This table displays the results of Business sector breakdown. The information is grouped by Sector (appearing as row headers), Percent share of operating locations, calculated using percent units of measure (appearing as column headers).
| Sector |
Percent share of operating locations |
| percent |
| Goods only |
23.2 |
| Hybrid goods |
2.2 |
| Services only |
74.6 |
| Total business sector |
100.0 |
This breakdown by industry could have a significant
effect since firms are expected to behave differently within the business
sector. For instance, goods producers have an incentive to keep their
production facilities close by in order to minimize the cost of managing their
facilities (Duranton and Puga 2005) and/or to benefit from various localization
economies (e.g., upstream—downstream links, labour market pooling, and knowledge spillovers).
Service producers, on the other hand, do not face the same costs of managing
multiple units across distances, since the production process is often (but not
always) less complicated than that for goods production. Expansion of goods and
services firms into new markets may also have a differential effect on trade.
For many services firms, because they require customer contact (e.g., retail
stores), expansion usually entails seeking new geographic markets, while
attempting not to take customers away from existing facilities (substitution
effect).
Of course, services firm expansions may
also induce trade if expansion into new areas involves the extension of
pre-existing supply chains. The same incentives may also hold for goods-producing
firms, but expansion may also induce more trade through upstream—downstream trade within the firm (complementary effect). Finally, with
respect to the hybrid goods sector, since firms in this sector are multiunit by
definition, they are likely larger than goods-only or services-only
enterprises. Hence, while they also face costs of managing multiple units
across distances, they are more likely to have the capacity to absorb these
costs if they are fixed. As a result, it is possible that these firms expand
more easily across provincial borders. How multiunit firm expansion relates to
trade will depend on the relative concentration of goods- and services-producing
units within the firm itself, and therefore is an empirical question.
3.3 Trade data
To measure regional trade flows, Statistics
Canada’s Surface Transportation File (STF) is used (please see the Appendix for
more detail on the construction of the file). It is a shipment-level database
on regional trade in Canada from 2004 to 2012, which covers goods moved by
truck and rail. Trade flows are benchmarked to inter- and intra-provincial
trade totals by commodity and year to better reflect total goods trade in
Canada. The database contains shipments measured in terms of commodity,
tonnage, value, distance, and cost between geocoded origins and destinations.
The latter allows the study to measure trade between a virtually limitless
number of geographies. This is important in light of the problems associated
with geographic aggregation, notably, the Modifiable Areal Unit Problem.
Generally speaking, how geographical units are specified, whether they are
standard or non-standard, matters and can impact spatial interaction models
like the gravity model employed here.
With this in mind, the study uses two
standard geographies, provinces and greater economic regions (GERs),
and one non-standard geography, hexagonal lattices (see Map 1), to measure
trade flows.Note 5 The study follows Bemrose, Brown, and Tweedle (2017) in using
hexagonal lattices with 225-km sides. Using postal codes of the operating
locations, the study constructs the GER and hexagonal geographies. While not
eliminating it completely, this strategy helps mitigate the sensitivity of the
results to biases associated with geographic aggregation that plague standard
geographies, since hexagons are identical and spatially independent (Arbia 1989).
Note that hexagons that cross provincial borders are split and treated as
separate units.
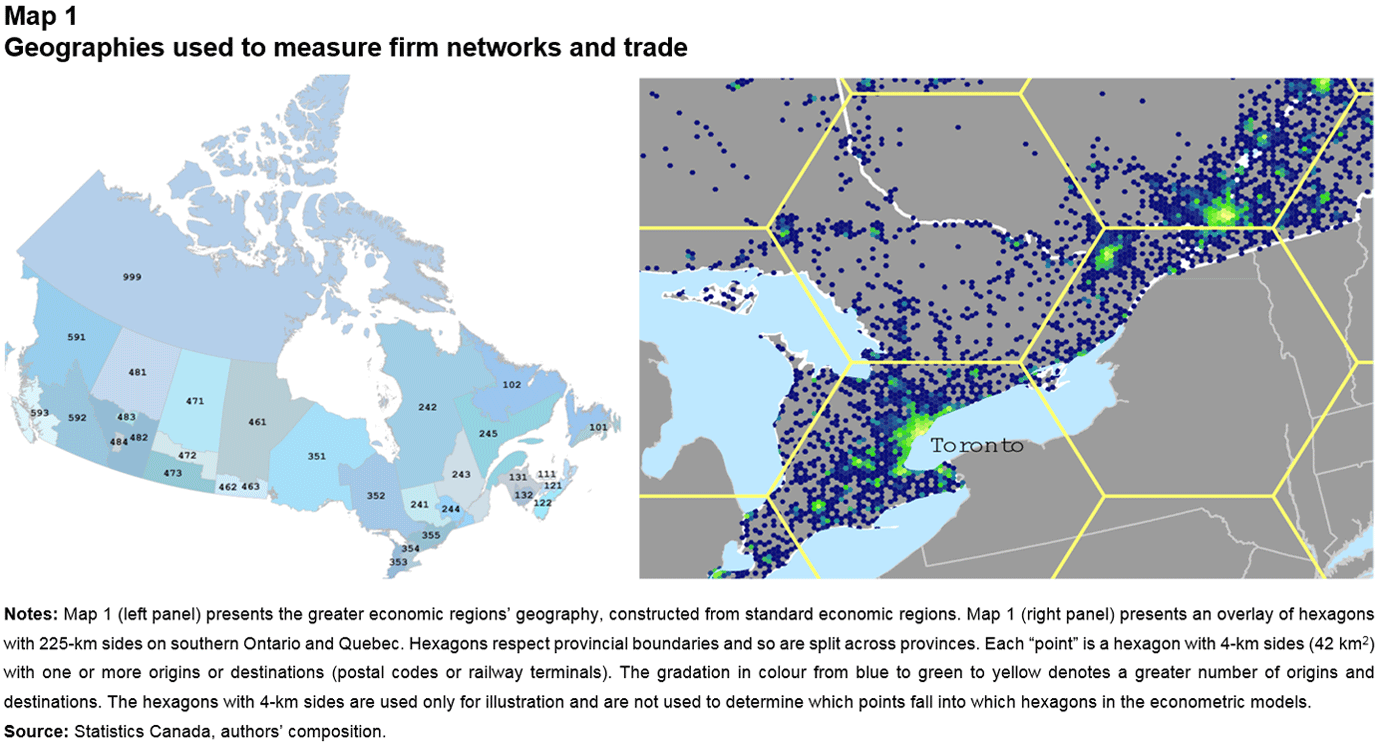
Description for Map 1
The title of Map 1 is “Geographies used to measure firm networks and trade.”
Map 1 consists of two panels (left and right).
Map 1 (left panel) is a map of the greater economic regions of Canada, which are shown in various shades of colour and identified with three-digit numbers (for illustration purposes).
Map 1 (right panel) is a map of the density of locations in the Surface Transportation File, along with the hexagonal lattices that make up the geography in the paper. It depicts southern Ontario and part of Quebec. The location of Toronto is indicated on the map.
The figure notes below give more information.
Notes: Map 1 (left panel) presents the greater economic regions’ geography, constructed from standard economic regions. Map 1 (right panel) presents an overlay of hexagons with 225-km sides on southern Ontario and Quebec. Hexagons respect provincial boundaries and so are split across provinces. Each “point” is a hexagon with 4-km sides (42 km2) with one or more origins or destinations (postal codes or railway terminals). The gradation in colour from blue to green to yellow denotes a greater number of origins and destinations. The hexagons with 4-km sides are used only for illustration and are not used to determine which points fall into which hexagons in the econometric models.
The source of Map 1 is “Statistics Canada, authors’ composition.”
For additional information, please contact Statistics Canada at STATCAN.infostats-infostats.STATCAN@canada.ca.
To this end, trade flows between origin and
destinations are measured at these different geographies. In a similar fashion,
it was possible to measure firm networks between the different levels of
geography as a result of the availability of geocoded postal code data on the
BR. Therefore, the resulting dataset measures not only trade flows between a
particular origin and destination pair, but also the number of operating
locations in the origin that belong to firms with locations also in the
destination, from 2004 to 2012. In this way, the study is also able to measure
firm networks at different levels of geography.
The data
are limited in the sense that they do not allow for identifying firms trading
with each other; that is, only regions can be identified. Identification stems
from variation in firm network ties across region pairs and through time. This
empirical strategy, however, could provide considerable insight. It provides a
means to examine whether the well documented trade border effect is also present
in firm networks. These data also serve to test whether networks matter for trade
across regions, and whether they act as a complement or substitute on aggregate
and by industry sector. Although the
age of the data may be viewed as a limitation, the basic underlying
relationship between firm networks, trade and provincial border effects are
unlikely to change significantly over time. For instance, provincial border
effects themselves have proven to be highly persistent with no identifiable
upward or downward trend between 2004 and 2012 (Bemrose, Brown and Tweedle
2017).
The next section (Section 4) begins the
analysis by examining the extent to which firm networks are affected by
distance and provincial border effects after taking into account the relative
size of firm-linked region pairs, by industry sector. This is followed by an
analysis of firm networks on trade (Section 5).
4 Analysis of firm networks
It is well established in the trade
literature that distance and provincial borders affect the level of intra- and
inter-provincial (or regional) trade in Canada (Agnosteva, Anderson, and Yotov 2014; Bemrose, Brown, and Tweedle 2017; Albrecht and Tombe 2016).
In a similar fashion, the study asks how easily firm networks spill across
provincial borders, all else being held equal. Initially, this entails the
development of an empirical framework that, while not developed from explicit
micro-foundations, provides some essential guidance as to how the spatial
extent of networks across regions can be estimated.
4.1 Firm network model
The model is based on a very simple
counterfactual premise. That is, if there are no costs associated with the
construction/purchase and operation of locations across space—i.e., no friction of distance—then the expected probability that an operating location in is part of a firm operating
in should be a function of the
number of firms operating in () and their underlying likelihood () of being a multiunit firm.
This, in turn, will depend on a vector () that characterizes the
population of firms in (e.g., their industry, size,
and managerial structure). Therefore, the expected share of operating locations
in that are part of a firm
operating in should be a function of ’s () weighted share of all
firms. In formal terms, this can be expressed as
From Equation (3), the proportion of
multiunit operating locations ()Note 6 in linked to , , relative to the counterfactual is defined as
assuming no friction of distance across
space, the expectation is that =1. But, if there is a cost
of developing firm networks across space, then the expectation would be that .Note 7 Solving (4) for results in:
which can be estimated by log linearising
and accounting for the unknowns , , and . This is accomplished by defining and substituting fixed
effects for and, to simplify matters, for . , which accounts for variation in costs of managing networks across
space, is defined as follows:
where is the distance between and and and are inter-provincial and
inter-regional binary variables, respectively. Hence, the strength of network
links between and is a function of the
propensity of to generate and to absorb network links
conditioned on the costs associated with establishing and operating units
across distance and borders. Following Head and Mayer (2014), we use Poisson
pseudo-maximum likelihood (Poisson-PML) to estimate the above equation in
cross-sectional form:
where is a multiplicative error
term. We estimate (7) across all three geographies (i.e., provinces, GERs, and
hexagonal lattices [225 km per side]) for the business sector as a whole and each
of the sectors. The analysis begins at the provincial level and then moves to
the sub-provincial level.
4.2 Provincial firm networks
The analysis at the provincial level of aggregation proceeds initially by developing a basic description of the pattern of network connections across provinces by sector. This provides some initial intuition for the model estimates that follow when Equation (7) is estimated, delivering the first test of hypotheses H1 and H2, namely that firm networks dissipate with distance and across provincial borders.
4.2.1 Describing firm networks
To begin, it is helpful to look at the relative importance of multiunit firms in Canada. Table 2 presents the firm structure and sector breakdown of operating locations across the business sector. The majority of operating locations in the business sector are part of single-location firms (90.9%) rather than multiunit firms (9.1%). However, multiunit firms are a large contributor to the Canadian economy: they comprise just over 40% of all employment.Note 8 The goods-only sector consists primarily of operating locations that are simple in nature (98.6%), while the services-only sector has more locations that belong to multiunit firms (8.8%). By their definition, all operating locations in the hybrid goods sector belong to multiunit firms.
As the analysis seeks to test the effect of provincial borders on firm networks, it presents the share of multiunit locations that are part of firms with locations in two or more provinces. As a whole, 69.3% of operating locations belonging to multiunit firms in the business sector are also multiple-province. This largely reflects the high share of hybrid goods, where 85.2% of operating locations are multiple-province. The shares for the services-only (65.7%) and goods-only sectors (33.3%) are somewhat lower.
Table 2
Operating locations by firm structure and sector
Table summary
This table displays the results of Operating locations by firm structure and sector. The information is grouped by Sector (appearing as row headers), Firm structure, Total, Single, Multiple and Multiple province, calculated using percent units of measure (appearing as column headers).
| Sector |
Firm structure |
| Total |
Single |
Multiple |
Multiple province |
| percent |
| Goods only |
100.0 |
98.6 |
1.4 |
33.3 |
| Services only |
100.0 |
91.2 |
8.8 |
65.7 |
| Hybrid goods |
100.0 |
Note ...: not applicable |
100.0 |
85.2 |
| Total business sector |
100.0 |
90.9 |
9.1 |
69.3 |
The intensity of firm network ties across
provincial borders can be calculated by taking the number of operating
locations in province linked to province as a share of all multiunit-firm
operating locations: . The number of multiunit firm operating locations in the province is
used, in order to normalize its outward ties because these form the pool of
units whose firms have the potential to have links to other provinces. To make
this concrete, Table 3 presents provincial firm networks for Ontario, using the
sectoral breakdown described above.
For the
total business sector, a cursory look at the shares suggests that operating
locations that belong to multiple-province firms tend to be concentrated close
to the province of operation. That is, most multiunit enterprises do not have
operations outside of the province. When they do, there is a tendency, albeit
not universally so, for their ties to dissipate with distance. For example, of
all operating locations in the business sector in Ontario, 30.9% also belong to
firms with operations in Quebec. These links dissipate as one moves east, with 22.8%
also belonging to firms in New Brunswick, 24.3% in Nova Scotia, 14.7% in Prince
Edward Island, and 18.8% in Newfoundland and Labrador. There are stronger links
to the western provinces, with 30.9% of locations in Ontario also being linked
to Alberta and British Columbia.
These aggregate findings mask some
important sector differences. Note that the goods-only sector is highly
concentrated, with few links crossing provincial borders. While Quebec remains the
province most linked to Ontario, only 13.1% of operating locations in Ontario
belong to firms that also have operations in Quebec. These links drop quickly
with distance. Other than Alberta and British Columbia, other provincial shares
remain well under 5%. The services-only sector shows more provincial dispersion
in firm networks than goods. Ontario is more connected to the Western provinces
than anywhere else in this sector, with just above 28% of locations in Ontario
being linked to locations in Alberta and British Columbia. There are also
strong links with Quebec as before (27.5%), but also with New Brunswick (20.9%)
and Nova Scotia (22.3%). Finally, provincial firm networks in hybrid goods tend
to concentrate around neighbouring provinces, but they are also dispersed
across Canada. Notably, 50.4% of locations are linked to Quebec and 38.0% to Ontario’s
western neighbour, Manitoba.
Table 3
Provincial firm networks for Ontario by sector
Table summary
This table displays the results of Provincial firm networks for Ontario by sector. The information is grouped by Sector (appearing as row headers), Share of own province: Nij/Ni, N.L., P.E.I., N.S., N.B., Que., Ont., Man., Sask., Alta. and B.C., calculated using percent units of measure (appearing as column headers).
| Sector |
Share of own province:
|
| N.L. |
P.E.I. |
N.S. |
N.B. |
Que. |
Ont. |
Man. |
Sask. |
Alta. |
B.C. |
| percent |
| Goods only |
2.3 |
1.0 |
3.5 |
3.2 |
13.1 |
100.0 |
4.4 |
3.1 |
9.3 |
9.2 |
| Services only |
17.3 |
14.4 |
22.3 |
20.9 |
27.5 |
100.0 |
24.9 |
21.8 |
28.3 |
28.5 |
| Hybrid goods |
28.2 |
18.6 |
37.3 |
35.3 |
50.4 |
100.0 |
38.0 |
34.6 |
47.0 |
45.9 |
| Total business sector |
18.8 |
14.7 |
24.3 |
22.8 |
30.9 |
100.0 |
26.6 |
23.5 |
30.9 |
30.9 |
As shown by the example of Ontario,
provincial economies are connected by firm links. Firm links that cross
provincial borders are more likely to be with neighbouring provinces. Provinces
with larger markets (e.g., British Columbia and Alberta in the example of
Ontario firm networks) come next. While the descriptive analysis points to the
importance of distance and provincial borders across the industry sectors, it
is a limited test focusing on one province with no control for the ability of
the destination region () to absorb network ties.
Equation (5) suggests that such a measure is necessary.
4.2.2 Model estimates
Table 4 presents regression results at the
provincial level across all sectors. The analysis focuses firstly on the
business sector (Model 1). Findings show that firm network ties decline with
distance and, when crossing provincial borders as a result of the provincial
border effect. A provincial border effect
of 0.71 implies that business sector firm networks are estimated to be 29%
lower across provinces than within them. Adding a squared term on distance to
take into account their potential non-linear effects results in insignificant
distance estimates and a modestly stronger border effect. As the next sub-section
will demonstrate, measuring networks across finer-grained geographies makes it
possible to better test whether distance has a non-linear effect on trade, and
whether border effects are sensitive to the geography chosen. The latter has
proven to be the case when one is measuring border effects on trade (e.g.,
Hillberry and Hummels 2008; Bemrose, Brown, and Tweedle 2017). Nevertheless,
these results are a basic test of the first two hypotheses, that distance has a
negative effect on networks (H1) and
that provincial borders do so as well (H2).
The results are expected to change,
particularly with respect to the influence of distance, when they are
disaggregated by sector. For goods producers (hybrid goods and goods-only), the
expectation is that firm networks will fall off quickly with distance, for the
reasons posited above (e.g., the higher cost of organizing goods production
across distances). This is borne out in the data. The effect of distance was
more strongly negative for the hybrid goods and goods-only sectors than for the
services sector. The provincial border effect was negative for the hybrid goods
and goods-only sectors, but significant solely for the goods-only sector. The services-only
sector, because it accounts for most of the business sector, produced results
that were broadly similar.
Table 4
Firm network () Poisson regression results by sector, provinces
Table summary
This table displays the results of Firm network (Nij) Poisson regression results by sector Business sector, Hybrid goods, Goods only and Services only (appearing as column headers).
|
Business sector |
Hybrid goods |
Goods only |
Services only |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
|
| Coefficient |
−0.146Note ** |
0.407 |
−0.211Note ** |
0.335 |
−0.586Note ** |
−0.777 |
−0.114Note ** |
0.440 |
| Standard error |
0.0197 |
0.3740 |
0.0172 |
0.3380 |
0.0777 |
0.8580 |
0.0213 |
0.3880 |
|
|
|
| Coefficient |
Note ...: not applicable |
−0.0373 |
Note ...: not applicable |
−0.0368 |
Note ...: not applicable |
0.0131 |
Note ...: not applicable |
−0.0373 |
| Standard error |
Note ...: not applicable |
0.0246 |
Note ...: not applicable |
0.0224 |
Note ...: not applicable |
0.0594 |
Note ...: not applicable |
0.0255 |
| Inter-province |
|
| Coefficient |
−0.347Note ** |
−0.483Note ** |
−0.00487 |
−0.139 |
−1.040Note ** |
−0.998Note ** |
−0.464Note ** |
−0.600Note ** |
| Standard error |
0.0835 |
0.1440 |
0.0705 |
0.1200 |
0.1610 |
0.2420 |
0.0898 |
0.1530 |
| Constant |
|
| Coefficient |
8.514Note ** |
6.609Note ** |
7.641Note ** |
5.765Note ** |
7.311Note ** |
7.971Note ** |
7.937Note ** |
6.032Note ** |
| Standard error |
0.138 |
1.290 |
0.133 |
1.166 |
0.584 |
2.915 |
0.144 |
1.343 |
| Observations (number) |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
| Border effect (value) |
0.71 |
0.62 |
1.00 |
0.87 |
0.35 |
0.37 |
0.63 |
0.55 |
4.3 Sub-provincial firm networks
Tables 5-1 and
5-2 presents regression results for firm networks using GERs and hexagons with 225-km sides. Intuitively,
these finer-grained geographies provide a stronger test of the effect of
provincial borders on networks, because they better represent the actual
pattern of network connections that tend to be smaller in scale, whereas the provinces,
particularly the large ones, tend to obscure these connections, possibly making
within-province networks look stronger than they are in reality. The use of finer-grained
geographies also promises to provide a more nuanced perspective on how firms
organize their production across space.
The effect of measuring firm networks
across sub-provincial geographies is to substantially reduce the estimated
border effect, but never to eliminate it altogether, regardless of the
geography or model specification used. Focusing on the business sector, for GERs, networks across provinces tend to be about 19% weaker than within
provinces. This result is qualitatively invariant across the two geographies
and model specifications. In magnitude, this is less than the estimated border
effect when provinces are used as units of analysis, but still economically
meaningful.
Across the three sectors—hybrid goods, goods-only, and services-only—provincial border effects tend to be weakest for hybrid goods and
strongest for goods-only, with services falling in the middle. This can be seen
most readily when the analysis focuses on the results using the quadratic
distance term (Model 2), which tends to consistently provide the lowest border
effect for goods. Why this is the case is open to interpretation. A reasonable
hypothesis is that, when the cost of acquiring or building new operating
locations across provincial borders is fixed (e.g., adapting to differing
regulatory systems), larger firms may be better able to amortize these costs
over a larger volume of sales. Consequently, if one thinks of hybrid goods
firms being the largest across the sectors, the results would be consistent
with this interpretation. More work is needed, however, to test this hypothesis
more thoroughly.
As noted earlier, goods-producing firms
have an incentive to keep production close by, while service producers may be
more inclined to seek new markets. As shown in Model 1, distance has the most
negative effect on networks for the goods-only and hybrid goods sectors
relative to those for the services-only sector. This holds irrespective of the
geography chosen. Furthermore, for goods producers, the inter-regional networks
are much weaker than the intra-regional networks, whereas this is not the case,
in relative terms, for the hybrid goods sector or the services-only sector.
This is consistent with the hypothesis that only over longer distances would
goods producers build facilities in order to expand into new markets. This is
observed with regard to the goods-only sector and in terms of measuring networks
using the hexagonal geography. There the squared term on distance is positive,
but weakly significant.
Finally, these estimates are repeated by
means of an employment-weighted network measure that accounts for the size of
operating locations for the business sector using the hexagonal geography.
These results in qualitatively similar estimates (see Table 9 in the Appendix).
Table 5-1
Firm network () regression results by sector — Greater economic regions
Table summary
This table displays the results of Firm network (Nij) regression results by sector — Greater economic regions Business sector, Hybrid goods, Goods only and Services only (appearing as column headers).
|
Business sector |
Hybrid goods |
Goods only |
Services only |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
|
| Coefficient |
−0.131Note ** |
0.4420Note ** |
−0.198Note ** |
0.5150Note ** |
−0.392Note ** |
1.5180Note ** |
−0.0996Note ** |
0.4070Note ** |
| Standard error |
0.00899 |
0.09110 |
0.00860 |
0.07190 |
0.06090 |
0.27400 |
0.00941 |
0.10300 |
|
|
| Coefficient |
Note ...: not applicable |
−0.0400Note ** |
Note ...: not applicable |
−0.0498Note ** |
Note ...: not applicable |
Note ...: not applicable |
Note ...: not applicable |
−0.0353Note ** |
| Standard error |
Note ...: not applicable |
0.00621 |
Note ...: not applicable |
0.00493 |
Note ...: not applicable |
0.02060 |
Note ...: not applicable |
0.00698 |
| Inter-province |
|
| Coefficient |
−0.206Note ** |
−0.240Note ** |
−0.0768Note ** |
−0.119Note ** |
−0.707Note ** |
−0.674Note ** |
−0.258Note ** |
−0.289Note ** |
| Standard error |
0.0246 |
0.0260 |
0.0207 |
0.0191 |
0.1160 |
0.0974 |
0.0280 |
0.0301 |
| Inter-region |
|
| Coefficient |
−0.235Note ** |
−0.493Note ** |
0.00469 |
−0.319Note ** |
−1.046Note ** |
−1.770Note ** |
−0.301Note ** |
−0.530Note ** |
| Standard error |
0.0497 |
0.0632 |
0.0476 |
0.0468 |
0.1230 |
0.1540 |
0.0518 |
0.0711 |
| Constant |
|
| Coefficient |
7.919Note ** |
6.197Note ** |
6.916Note ** |
4.777Note ** |
5.683Note ** |
−0.173 |
7.406Note ** |
5.880Note ** |
| Standard error |
0.0709 |
0.2780 |
0.0749 |
0.2240 |
0.3790 |
0.8700 |
0.0720 |
0.3130 |
| Observations (number) |
900 |
900 |
900 |
900 |
900 |
900 |
900 |
900 |
| Border effect (value) |
0.81 |
0.79 |
0.93 |
0.89 |
0.49 |
0.51 |
0.77 |
0.75 |
Table 5-2
Firm network () regression results by sector — Hexagons (225 km per side)
Table summary
This table displays the results of Firm network (Nij) regression results by sector — Hexagons (225 km per side) Business sector, Hybrid goods, Goods only and Services only (appearing as column headers).
|
Business sector |
Hybrid goods |
Goods only |
Services only |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
| Coefficient |
−0.154Note ** |
−0.107 |
−0.214Note ** |
0.126Table 5-2 Note † |
−0.617Note ** |
−1.224Note ** |
−0.121Note ** |
−0.184Note * |
| Standard error |
0.00664 |
0.08440 |
0.00598 |
0.07070 |
0.05570 |
0.32500 |
0.00736 |
0.09220 |
|
|
| Coefficient |
Note ...: not applicable |
−0.00320 |
Note ...: not applicable |
−0.0235Note ** |
Note ...: not applicable |
0.0445Table 5-2 Note † |
Note ...: not applicable |
0.00434 |
| Standard error |
Note ...: not applicable |
0.00581 |
Note ...: not applicable |
0.0049 |
Note ...: not applicable |
0.0241 |
Note ...: not applicable |
0.00634 |
| Inter-province |
|
| Coefficient |
−0.218Note ** |
−0.220Note ** |
−0.100Note ** |
−0.117Note ** |
−0.507Note ** |
−0.508Note ** |
−0.271Note ** |
−0.268Note ** |
| Standard error |
0.0181 |
0.0186 |
0.0144 |
0.0142 |
0.0824 |
0.0844 |
0.0217 |
0.0222 |
| Inter-region |
|
| Coefficient |
−0.177Note ** |
−0.197Note ** |
0.0583 |
−0.0901Table 5-2 Note † |
−0.734Note ** |
−0.517Note ** |
−0.247Note ** |
−0.220Note ** |
| Standard error |
0.0442 |
0.0561 |
0.0421 |
0.0506 |
0.1160 |
0.1580 |
0.0457 |
0.0586 |
| Constant |
|
| Coefficient |
4.094Note ** |
3.954Note ** |
3.128Note ** |
2.104Note ** |
1.666Note * |
3.425Note ** |
3.545Note ** |
3.735Note ** |
| Standard error |
0.0859 |
0.2700 |
0.1230 |
0.2360 |
0.7050 |
1.1260 |
0.0858 |
0.2950 |
| Observations (number) |
7,306 |
7,306 |
7,306 |
7,306 |
7,306 |
7,306 |
7,306 |
7,306 |
| Border effect (value) |
0.80 |
0.80 |
0.90 |
0.89 |
0.60 |
0.60 |
0.76 |
0.76 |
5 Firm networks and trade
The study now turns to the heart of the
analysis and asks two related questions. First, what are the magnitude and
direction of the influence of firm networks on trade between regions? In other
words, if networks matter, do they act as a complement to, or a substitute for,
trade? Second, are the magnitude and direction of the effect of firm networks
on trade conditional on trade costs, whether these costs are associated with
distance and/or provincial borders? As noted in the introduction, the intuition
is that, with rising trade costs associated with distance and borders, the cost
savings to firms from maintaining existing supply chains (be they internal or
external to the firm) may be exhausted, inducing firms to seek out new, closer
by suppliers. Hence, the expectation is that, with longer distances between
regions and borders, the effect of firm networks on trade will turn from
positive (a complementary effect) to negative (a substitution effect).
Econometrically, the study approaches this
in two steps. The first step maintains the cross-sectional approach used above.
This provides a basic test of the relationship between networks and trade, but
one that may be endogenous (e.g., as a result of missing-variable bias). This is
addressed, in the second step, by developing a panel of regions and using a
first-difference estimator.
5.1 Cross-sectional estimates
As is now standard in the literature, a
trade model is estimated that takes into account the capacity of geographic
units to generate and absorb trade and a measure of trade costs between them.
The model is specified as follows:
where is the value of goods
shipments between region and , and and take into account the ’s output and market
potential and ’s size and level of competition,
respectively. Trade costs () are accounted for by the
distance between and () and a set of binary
variables that account for inter-provincial () and inter-regional () trade effects:
Since firm networks are also expected to
reduce trade costs, their bilateral measure () is also included with the
other measures of trade costs. The analysis tests the effect of firm networks
in the business sector on trade.
For more discussion on the construction and
analysis using the multiplicative firm network measure, see the Appendix.
The model is estimated for the hexagons
with 225-km sides (Table 6). The baseline model, which excludes networks, is
Model 1. As expected, this model shows distance has a strong negative effect on
trade. The effect of provincial borders on trade, as expected, is negative and
indicates inter-provincial trade is about 59%
of the level of
intra-provincial trade, all else being held equal. Although a more parsimonious
model is used here, this result is qualitatively similar to the findings of Bemrose,
Brown and Tweedle (2017).
Model 2 includes the additive measure of
business sector firm networks. The effect of firm networks on trade is positive.
This suggests, at least on the basis of the cross-sectional evidence, that firm
networks on balance tend to complement, rather than act as a substitute for,
trade. Their inclusion, however, reduces the effect of provincial borders on
trade by about half.
Table 6
The impact of business sector firm networks on trade flows (
), cross-sectional regression results for hexagons (225 km per side)
Table summary
This table displays the results of The impact of business sector firm networks on trade flows (Xij) Model 1 and Model 2 (appearing as column headers).
|
Model 1 |
Model 2 |
|
|
| Coefficient |
−0.828Note ** |
−0.792Note ** |
| Standard error |
0.0635 |
0.0673 |
| Inter-province |
|
| Coefficient |
−0.466Note ** |
−0.236Note * |
| Standard error |
0.0875 |
0.1010 |
| Inter-region |
|
| Coefficient |
0.1200 |
0.0948 |
| Standard error |
0.1280 |
0.1300 |
|
|
|
| Coefficient |
Note ...: not applicable |
0.585Note ** |
| Standard error |
Note ...: not applicable |
0.111 |
| Constant |
|
| Coefficient |
17.13Note ** |
14.10Note ** |
| Standard error |
0.763 |
−1.031 |
| Observations (number) |
7,306 |
7,189 |
5.2 Panel estimates
As noted above, owing to missing-variable
bias and reverse causality, the cross-sectional estimates may be endogenous
with respect to the network measure. Reverse causality may be a concern,
because rising trade might provide an incentive for firms to build operating
locations in these new markets. However, to date, much of the empirical and
theoretical evidence suggests trade flows follow the expansion of networks—that is, firms use their contacts (i.e., their network) to find new
markets (Chaney 2014). On this basis, reverse causality does not appear to be a
major source of bias. Missing-variable bias may result from unaccounted
differences in industry structure. Assuming these are fixed over short periods,
first-differencing also allows the study to test further the effect of trade
costs on firm networks. As trade costs rise, the expectation is that the effect
of networks on trade will shift from complementing trade (positive) to
substituting for trade (negative). Testing for this addresses hypotheses H3 and H4. Because trade costs are expected to be positively related to
distance and provincial borders, the analysis conditions the effect of network
growth () on trade growth by the
distance between regions () and whether the flow
crosses provincial borders (). Formally, the model is
specified as follows:
with the lagged level of trade () included to account for regression to the
mean. In order to reduce the effect of noise in the data, the study divides the
9-year panel into three sub-periods (), 2004 to 2006, 2007 to 2009, and 2010 to
2012, with the mean of the variables calculated across years within each
period.Note 9 Finally, period fixed effects () are included to account for inflation and
macro shocks. The periods are then differenced to obtain (10), which is
estimated using ordinary least squares (OLS).
Turing to the results, the analysis begins with
estimating the effect of business sector (goods and services) firm networks on
trade across two geographies—GERs
and hexagons with 225-km sides, presented in Tables 7-1 and 7-2. The
impact of firm networks in the business sector on trade is negative and
significant only for the GERs (see Table 7-1, Model 1). The
relationship between networks and trade becomes much clearer when its effect is
conditioned on distance and provincial borders. In terms of the business sector
results for GERs, the effect of firm networks on trade is positive.Note 10 However, their effect falls with distance and provincial borders (see
Table 7-1, Model 2). This holds also for the sectors—hybrid goods, goods-only, and services-only—across both geographies, albeit at times more weakly so,
particularly for goods-only firm network effects. Using the GER results,
at just over 3,300 km, the effect of business sector firm networks on trade
turns negative, switching from a complement to a substitute for trade.Note 11 This is a little under the driving distance from Toronto to Calgary. This
finding obviously implies that trade must cross provincial borders. The
conditioning effect of provincial borders on the influence of networks on trade
is also negative and significant for both geographies. According to the GER estimates,
if trade flows cross a provincial border, the effect of firm networks on trade
turns negative at just over 1,200 km. Hence, taking a page from Engel and
Rogers (1996), the provincial border effect is equivalent to adding 2,100 km to
the journey between provinces. A journey of this distance would incur an ad valorem transportation cost of about
5.7% (Behrens and Brown 2018). The implication is that, for many important
inter-provincial region pairs (e.g., Ontario—Alberta), the effect of firm networks on trade is negative. These
results are consistent with hypotheses H3 and H4. That is, as trade costs
rise—from distance and borders—firm networks move from being a complement to being a substitute for
trade flows as production (H3) and
sourcing of inputs (i.e., supply chains) (H4)
shift towards the destination.
Table 7-1
The impact of additive firm networks on trade flows (), first difference panel model — Greater economic regions
Table summary
This table displays the results of The impact of additive firm networks on trade flows (ΔXij) Business sector, Hybrid goods, Goods only and Services only (appearing as column headers).
|
Business sector |
Hybrid goods |
Goods only |
Services only |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
| Coefficient |
−0.300Note ** |
−0.420Note ** |
−0.278Note ** |
−0.332Note ** |
−0.196Note ** |
−0.223Note ** |
−0.310Note ** |
−0.408Note ** |
| Standard error |
0.0444 |
0.0527 |
0.0425 |
0.0475 |
0.0304 |
0.0328 |
0.0450 |
0.0516 |
|
|
|
| Coefficient |
−5.263Note ** |
35.350Note ** |
0.145 |
16.580Note ** |
−0.156Table 7-1 Note † |
2.138Note ** |
−4.284Note ** |
31.740Note ** |
| Standard error |
1.2600 |
5.0140 |
0.5000 |
3.0210 |
0.0817 |
0.4960 |
1.2610 |
4.9230 |
|
|
|
| Coefficient |
Note ...: not applicable |
−4.467Note ** |
Note ...: not applicable |
−1.761Note * |
Note ...: not applicable |
−0.355Table 7-1 Note † |
Note ...: not applicable |
−4.293Note ** |
| Standard error |
Note ...: not applicable |
1.213 |
Note ...: not applicable |
0.743 |
Note ...: not applicable |
0.182 |
Note ...: not applicable |
1.188 |
|
|
|
| Coefficient |
Note ...: not applicable |
−4.363Note ** |
Note ...: not applicable |
−1.923Note ** |
Note ...: not applicable |
−0.256Note ** |
Note ...: not applicable |
−3.733Note ** |
| Standard error |
Note ...: not applicable |
0.582 |
Note ...: not applicable |
0.396 |
Note ...: not applicable |
0.066 |
Note ...: not applicable |
0.559 |
| Observations (number) |
1,740 |
1,740 |
1,740 |
1,740 |
1,206 |
1,206 |
1,740 |
1,740 |
| R-squared |
0.190 |
0.245 |
0.173 |
0.199 |
0.176 |
0.194 |
0.194 |
0.237 |
Table 7-2
The impact of additive firm networks on trade flows (), first difference panel model — Hexagons (225 km per side)
Table summary
This table displays the results of The impact of additive firm networks on trade flows (ΔXij) Business sector, Hybrid goods, Goods only and Services only (appearing as column headers).
|
Business sector |
Hybrid goods |
Goods only |
Services only |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
| Coefficient |
−0.349Note ** |
−0.372Note ** |
−0.353Note ** |
−0.367Note ** |
−0.235Note ** |
−0.248Note ** |
−0.353Note ** |
−0.379Note ** |
| Standard error |
0.0156 |
0.0177 |
0.0160 |
0.0166 |
0.0302 |
0.0305 |
0.0159 |
0.0177 |
|
|
|
| Coefficient |
0.077 |
10.400Note ** |
0.772Note ** |
6.615Note ** |
−0.204Note ** |
1.089Note * |
−0.474 |
9.856Note ** |
| Standard error |
0.3440 |
3.9270 |
0.2690 |
1.5650 |
0.0673 |
0.4830 |
0.3060 |
2.9270 |
|
|
|
| Coefficient |
Note ...: not applicable |
−1.644Note * |
Note ...: not applicable |
−0.984Table 7-2 Note † |
Note ...: not applicable |
−0.324 |
Note ...: not applicable |
−1.994Note ** |
| Standard error |
Note ...: not applicable |
0.663 |
Note ...: not applicable |
0.563 |
Note ...: not applicable |
0.226 |
Note ...: not applicable |
0.678 |
|
|
|
| Coefficient |
Note ...: not applicable |
−1.256Note * |
Note ...: not applicable |
−0.670Note ** |
Note ...: not applicable |
−0.143Table 7-2 Note † |
Note ...: not applicable |
−1.221Note ** |
| Standard error |
Note ...: not applicable |
0.5400 |
Note ...: not applicable |
0.2360 |
Note ...: not applicable |
0.0816 |
Note ...: not applicable |
0.4040 |
| Observations (number) |
5,389 |
5,389 |
5,241 |
5,241 |
1,736 |
1,736 |
5,337 |
5,337 |
| R-squared |
0.210 |
0.223 |
0.209 |
0.213 |
0.179 |
0.187 |
0.214 |
0.230 |
6 Conclusions
This paper provides a picture of firm networks and intra- and inter-provincial trade
patterns in Canada. Firm networks, like trade flows, are negatively influenced
by both distance and borders. This is apparent in the descriptive statistics
and perhaps more so in their estimated effects. These patterns are consistent
with higher costs associated with managing operating units across longer
distances and establishing operations in a different province. In turn, firm
networks tend to be positively associated with trade flows—that is, they act as a complement
to trade. However, the effect of firm networks on trade is conditional on
variables associated with higher trade costs. Namely, with rising distance and
provincial borders, the complementary effect of firm networks on trade falls
and, at sufficiently long distances and when crossing borders, networks switch
from being a complement to trade to being a substitute instead. Hence,
provincial borders appear to reduce both the degree to which the economy is
knit together through firm networks and the degree to which these networks are
able to facilitate trade. In fact, the study finds that, after accounting for
firm networks, the estimated provincial border effect coefficient fall by about
half.
There are, of course, many extensions that might be made to this
analysis. Through input—output tables, the upstream—downstream nature of the linked operating units can be defined, providing a better measure
of the degree to which trade reflects these functional relationships. The
ultimate next step, however, would be to move from measures of networks and
flows across aggregate regions, whereby the pure effect of intra-firm trade is
obscured, to a database where shipments within and across firms are measured.
With detailed information on the location of where shipments are picked up and
dropped off, combined with information on the location and industry of units on
the Business Register, and other sources, it may be possible to build such a
database. The analysis will
be extended once more recent data become available. However, because the
relationships identified are highly persistent, the results discussed in this
study are unlikely to change over time. This is a step that will be taken as
the opportunity arises.
7 Appendix
7.1 Surface Transportation File
Trade data are available from Statistics
Canada’s Surface Transportation File (STF). The STF combines data from the
Trucking Commodity Origin and Destination Survey (TCOD) and
railway waybills for the years from 2002 to 2012, and provides estimates on the
value of goods trade between regions in Canada and between Canada and the
United States. Note that it excludes goods moved by air, pipeline, and water.
The STF also provides data on network
distance—that is, the actual distance travelled for a shipment of goods. This
gives a most accurate measure of the distance goods travel within and between
regions in Canada. For this paper, network distance is available for the entire
sample down to greater economic region pairs. For the hexagons with 225-km sides,
there are hexagon pairs with missing network distance data. In these cases,
great-circle distance, a measure commonly used in the literature, is converted to
network distance using a model. This is done by regressing network distance on
a polynomial of great-circle distance and using predicted values for the
missing data. For own-hexagon pairs, the great-circle distance within the hexagon
is measured as the radius of a circle at equal area to that of the hexagon. A
detailed description of the STF and its development is provided in Bemrose, Brown, and Tweedle (2017).
7.2 Additional results
There are alternatives to the network
measure used in the study. Here, a measure based on the mathematical definition
of a network (or graph), which may be more familiar to some readers, is
described. Recall that the goal of this study is to describe firm networks across
regions, and later to see how those firm networks can facilitate trade.
Consider the network of the firm , , where the nodes, , are operating locations. Nothing is known regarding the
relationships between operating locations other than they are controlled by the
same firm. It is assumed that the network is complete, which means there are
edges between every pair of nodes and in .
The graph of firm networks at the level of
the aggregate economy is the union of all of the individual firm networks,
Turning to the effect of networks on trade,
trade happens at a regional level, across and within firms. So it makes sense
to translate the graph into a regional graph where
the nodes are regions, and edges are weighted to reflect the density of firm
connections in the underlying between region pairs.
Now the regional network is , where are regions, which could be
provinces or economic regions or other geography. The problem is then to translate
the set of sets of firm edges () into the set of regional
edges (). There are a few options for
achieving this, while it bears noting that the purpose is to represent what the
firm network means for goods trade.
The basic idea is to add up the edges
across regions within each firm, and then aggregate across all firms in the
economy. This gives an edge weight in the regional network of
where is a firm, and are locations and and are regions. In the simplest case, each firm
edge has weight 1. To align with the notation used
in the body of the paper, write the number of nodes in a network as , which makes the measure
Description for Figure 2
The title of Figure 2 is “Conceptual firm networks, multiplicative.”
The diagram depicts possible connections between locations of a firm in different regions.
There are three regions, represented as hexagons, labelled Region , Region and Region . The hexagons are contiguous: they are joined on two sides and are delineated by a black line.
Firm has been location in Region (), two locations in Region (, ) and one location in Region ().
There are solid lines between all locations in Regions and , and dotted lines from those locations to the location in Region .
The source of Figure 2 is “Statistics Canada, authors’ composition.”
It follows that each location must divide
its attention between the other locations (in goods terms, if a location is
trading with the other locations in a firm, it must divide the physical goods
it is sending among the locations, with a similar argument for intermediate
inputs, time spent communicating, and making contacts). Consider the geography pair once more:
each location in is a potential trading
partner of all the firm’s locations in . As can be seen in Figure 2, within a firm there are two links
between and . However, there are links in region as well. In this instance,
the strength of bilateral firm links between region and is the number of potential links between and scaled down by the number of locations of
the firm in all regions. In mathematical terms, this translates to weighting
each edge by the total number of locations in each firm, . Plugging those weights into the aggregation equations yields the
following:
In the paper, this measure is termed , where is a mnemonic for “multiplicative.”
It parallels the work of Combes, Lafourcade and Mayer (2005) and Garmendia et
al. (2012). However, these authors do not discount networks by the number of
units in the firm, as in Equation (2).
The number of
units in a firm provides a straightforward measure of firm size, but one that
may not be complete. For example, the question easily arises of whether it is
appropriate to treat networks of convenience stores and supermarkets with the
same number of units as equivalent. While both may have the same network ties
between two regions, supermarkets are likely larger in terms of employment. Employment
may, in turn, impact trade flows, since larger firms have the capacity to
generate more cross-region trade. In the network setup, it is simple to
incorporate employment weights into the firm edge weights, by changing the edge
weight from to , where is the employment at location of firm , and is total employment at firm . The analysis, therefore, takes
the additional step of weighting the counts by employment. When this is applied,
however, no qualitative difference in the results are found.
7.2.1 Multiplicative firm networks
Tables 8-1 and 8-2 present results of the
association between multiplicative firm networks and trade flows by GER and
hexagons with 225-km sides using a first-difference panel model. The effect of
the multiplicative firm networks measure is largely insignificant. For the GER results
(Table 8-1), there are only significant estimates for the fully specified model
using firm networks in the hybrid goods sector. Firm networks positively impact
trade flows, but do so to a lesser extent for regions that are further away (as
is shown by the negative coefficient on the interaction term between firm
networks and distance). This is consistent with the main findings of this study.
On the other hand, unlike the study’s main results, inter-provincial firm
networks increase their positive impact on trade. All of these findings
disappear when hexagons with 225-km sides are used (Table 8-2), where results
are insignificant for all fully specified models.
7.2.2 Employment-weighted firm networks
The
three key network measures (, , and ) used in this study are expanded to their
employment-weighted versions. More specifically, Equation (1) can be redefined
as follows:
where is the employment of operating locations of
firm in region (that also have locations in ). Similarly, Equations (2) and (3) may also
be rewritten as follows:
The aggregate additive measure thus represents the employment-weighted
network links between and . Note that
the multiplicative measure, , is now normalized by the total employment of the firm, . Tables 9, 10 and 11 present re-estimates of the main findings using employment-weighted
firm networks for the business sector for hexagons with 225-km sides. All of
the results hold, with the extent of firm networks negatively influenced by
distance and borders, the inclusion of the firm networks measure reducing the
provincial border effect by about half, and with the positive influence of firm
networks on trade falling with distance and when crossing borders.
Table 8-1
The impact of multiplicative firm networks on trade flows (), first difference panel model — Greater economic regions
Table summary
This table displays the results of The impact of multiplicative firm networks on trade flows (ΔXij) Business sector, Hybrid goods, Goods only and Services only (appearing as column headers).
|
Business sector |
Hybrid goods |
Goods only |
Services only |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
| Coefficient |
−0.279Note ** |
−0.279Note ** |
−0.277Note ** |
−0.285Note ** |
−0.189Note ** |
−0.189Note ** |
−0.282Note ** |
−0.282Note ** |
| Standard error |
0.0426 |
0.0428 |
0.0425 |
0.0425 |
0.0298 |
0.0298 |
0.0427 |
0.0429 |
|
|
|
| Coefficient |
−0.117 |
0.1750 |
−0.0180 |
2.1400Note * |
0.0039 |
−0.394 |
−0.335 |
−0.115 |
| Standard error |
0.2870 |
1.8700 |
0.1550 |
0.9660 |
0.0413 |
0.3640 |
0.2490 |
1.4920 |
|
|
|
| Coefficient |
Note ...: not applicable |
0.4070 |
Note ...: not applicable |
2.1630Note ** |
Note ...: not applicable |
−0.0527 |
Note ...: not applicable |
−0.888 |
| Standard error |
Note ...: not applicable |
1.185 |
Note ...: not applicable |
0.587 |
Note ...: not applicable |
0.171 |
Note ...: not applicable |
0.908 |
|
|
| Coefficient |
Note ...: not applicable |
−0.0891 |
Note ...: not applicable |
−0.540Note ** |
Note ...: not applicable |
0.0574 |
Note ...: not applicable |
0.0826 |
| Standard error |
Note ...: not applicable |
0.3610 |
Note ...: not applicable |
0.1870 |
Note ...: not applicable |
0.0533 |
Note ...: not applicable |
0.2920 |
| Observations (number) |
1,740 |
1,740 |
1,740 |
1,740 |
1,206 |
1,206 |
1,740 |
1,740 |
| R-squared |
0.173 |
0.173 |
0.173 |
0.181 |
0.172 |
0.173 |
0.175 |
0.176 |
Table 8-2
The impact of multiplicative firm networks on trade flows (), first difference panel model — Hexagons (225 km per side)
Table summary
This table displays the results of The impact of multiplicative firm networks on trade flows (ΔXij) Business sector, Hybrid goods, Goods only and Services only (appearing as column headers).
|
Business sector |
Hybrid goods |
Goods only |
Services only |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
| Coefficient |
−0.350Note ** |
−0.350Note ** |
−0.349Note ** |
−0.349Note ** |
−0.230Note ** |
−0.230Note ** |
−0.351Note ** |
−0.351Note ** |
| Standard error |
0.0156 |
0.0156 |
0.0159 |
0.0159 |
0.0297 |
0.0297 |
0.0158 |
0.0158 |
|
|
|
| Coefficient |
−0.156Note * |
−0.837 |
−0.118Note ** |
−0.256 |
−0.0500 |
−0.0840 |
−0.142Note * |
−0.183 |
| Standard error |
0.0725 |
0.5560 |
0.0453 |
0.3060 |
0.0416 |
0.4060 |
0.0665 |
0.4300 |
|
|
|
| Coefficient |
Note ...: not applicable |
−0.0929 |
Note ...: not applicable |
0.0951 |
Note ...: not applicable |
0.1300 |
Note ...: not applicable |
0.1040 |
| Standard error |
Note ...: not applicable |
0.224 |
Note ...: not applicable |
0.11 |
Note ...: not applicable |
0.182 |
Note ...: not applicable |
0.178 |
|
|
|
| Coefficient |
Note ...: not applicable |
0.10300 |
Note ...: not applicable |
0.00885 |
Note ...: not applicable |
−0.0101 |
Note ...: not applicable |
−0.00496 |
| Standard error |
Note ...: not applicable |
0.0895 |
Note ...: not applicable |
0.0458 |
Note ...: not applicable |
0.0672 |
Note ...: not applicable |
0.0693 |
| Observations (number) |
5,389 |
5,389 |
5,241 |
5,241 |
1,736 |
1,736 |
5,337 |
5,337 |
| R-squared |
0.211 |
0.212 |
0.208 |
0.208 |
0.175 |
0.176 |
0.214 |
0.214 |
Table 9
Employment-weighted business sector firm network () Poisson regression results for 225-km-sided hexagons
Table summary
This table displays the results of Employment-weighted business sector firm network (Eij) Poisson regression results for
225-km-sided hexagons Model 1 and Model 2 (appearing as column headers).
|
Model 1 |
Model 2 |
|
|
|
| Coefficient |
−0.154Note ** |
−0.0582 |
| Standard error |
0.00757 |
0.09510 |
|
|
| Coefficient |
Note ...: not applicable |
−0.00667 |
| Standard error |
Note ...: not applicable |
0.00653 |
| Inter-province |
|
| Coefficient |
−0.165Note ** |
−0.169Note ** |
| Standard error |
0.0198 |
0.0203 |
| Inter-region |
|
| Coefficient |
−0.215Note ** |
−0.257Note ** |
| Standard error |
0.0474 |
0.0571 |
| Constant |
|
| Coefficient |
7.205Note ** |
6.914Note ** |
| Standard error |
0.118 |
0.314 |
| Observations (number) |
7,306 |
7,306 |
Table 10
The impact of employment-weighted business sector firm networks on trade flows (), cross-sectional regression results for 225-km-sided hexagons
Table summary
This table displays the results of The impact of employment-weighted business sector firm networks on trade flows (Xij) Model 1, Model 2 and Model 3 (appearing as column headers).
|
Model 1 |
Model 2 |
Model 3 |
|
|
|
| Coefficient |
−0.828Note ** |
−0.797Note ** |
−0.513Note ** |
| Standard error |
0.0635 |
0.0659 |
0.0694 |
| Inter-province |
|
| Coefficient |
−0.466Note ** |
−0.305Note ** |
−0.142Note * |
| Standard error |
0.0875 |
0.0966 |
0.0687 |
| Inter-region |
|
| Coefficient |
0.1200 |
0.0777 |
3.9600Note ** |
| Standard error |
0.128 |
0.128 |
0.463 |
|
|
|
| Coefficient |
Note ...: not applicable |
0.442Note ** |
Note ...: not applicable |
| Standard error |
Note ...: not applicable |
0.075 |
Note ...: not applicable |
|
|
|
| Coefficient |
Note ...: not applicable |
Note ...: not applicable |
0.339Note ** |
| Standard error |
Note ...: not applicable |
Note ...: not applicable |
0.0404 |
| Constant |
|
| Coefficient |
17.13Note ** |
13.44Note ** |
13.12Note ** |
| Standard error |
0.763 |
1.053 |
0.864 |
| Observations (number) |
7,306 |
7,189 |
7,189 |
Table 11
The impact of employment-weighted business sector firm networks on trade flows () for 225-km-sided hexagons, first difference panel model
Table summary
This table displays the results of The impact of employment-weighted business sector firm networks on trade flows (∆Xij) for 225-km-sided hexagons Additive measure (Eij) and Multiplicative measure (Eij ) (appearing as column headers).
|
Additive measure (
) |
Multiplicative measure () |
| Model 1 |
Model 2 |
Model 1 |
Model 2 |
|
|
|
| Coefficient |
−0.349Note ** |
−0.380Note ** |
−0.349Note ** |
−0.349Note ** |
| Standard error |
0.0156 |
0.0168 |
0.0155 |
0.0156 |
|
|
|
| Coefficient |
0.2540 |
5.1190Note ** |
−0.106Table 11 Note † |
−0.0516 |
| Standard error |
0.1710 |
1.1030 |
0.0589 |
0.2320 |
|
|
|
| Coefficient |
Note ...: not applicable |
−0.924Note ** |
Note ...: not applicable |
−0.0474 |
| Standard error |
Note ...: not applicable |
0.301 |
Note ...: not applicable |
0.172 |
|
|
|
| Coefficient |
Note ...: not applicable |
−0.612Note ** |
Note ...: not applicable |
−0.00289 |
| Standard error |
Note ...: not applicable |
0.1620 |
Note ...: not applicable |
0.0447 |
| Constant |
|
| Coefficient |
2.128Note ** |
2.643Note ** |
2.238Note ** |
2.243Note ** |
| Standard error |
0.747 |
0.753 |
0.746 |
0.746 |
| Observations (number) |
5,389 |
5,389 |
5,389 |
5,389 |
| R-squared |
0.211 |
0.228 |
0.222 |
0.211 |
References
Agnosteva, D.E., J.E. Anderson, and Y.V. Yotov. 2014. Intra-national Trade Costs: Measurement and Aggregation. NBER Working Paper, no. 19872. Cambridge, Massachusetts: National Bureau of Economic Research.
Albrecht, L., and T. Tombe. 2016. “Internal trade, productivity and interconnected industries: A quantitative analysis.” Canadian Journal of Economics / Revue canadienne d’économique 49 (1): 237–263.
Anderson, J.E. 2011. “The Gravity Model.” Annual Review of Economics 3 (1): 133–160.
Anderson, J.E., and E. van Wincoop. 2004. “Trade Costs.” Journal of Economic Literature 42 (3): 691–751.
Antràs, P. 2003. “Firms, Contracts, and Trade Structure.” The Quarterly Journal of Economics 118 (4): 1375–1418.
Antràs, P., and E. Helpman. 2004. “Global Sourcing.” Journal of Political Economy 112 (3): 552–580.
Arbia, G. 1989. Spatial Data Configuration in Statistical Analysis of Regional Economic and Related Problems. Dordrecht: Kluwer Academic Publishers.
Atalay, E., A. Hortaçsu, J. Roberts, and C. Syverson. 2011. “Network structure of production.” Proceedings of the National Academy of Sciences of the United States of America 108 (13): 5199–5202.
Atalay, E., A. Hortaçsu, and C. Syverson. 2014. “Vertical Integration and Input Flows.” American Economic Review 104 (4): 1120–1148.
Baldwin, J.R., D. Beckstead, and A. Girard. 2002. The Importance of Entry to Canadian Manufacturing with an Appendix on Measurement Issues. Analytical Studies Branch Research Paper Series, no. 189. Statistics Canada Catalogue no. 11F0019M. Ottawa: Statistics Canada.
Baldwin, J.R., and W.M. Brown. 2005. Foreign Multinationals and Head Office Employment in Canadian Manufacturing Firms. Analytical Studies Branch Research Paper Series, no. 34. Statistics Canada Catalogue no. 11F0019M. Ottawa: Statistics Canada.
Behrens, K., and W. M. Brown. 2018. “Transport Costs, Trade, and Geographic Concentration: Evidence from Canada.” In Handbook of International Trade and Transportation, ed. B. Blonigen and W. Wilson, chapter 6, p. 188–225. Cheltenham: Edward Elgar.
Behrens, K., and V. Sharunova. 2015. Inter- and intra-firm linkages: Evidence from microgeographic location patterns. CEPR Discussion Papers, no. DP 10921. London, United Kingdom: Centre for Economic Policy Research.
Belderbos, R., and L. Sleuwaegen. 1996. “Japanese Firms and the Decision to Invest Abroad: Business Groups and Regional Core Networks.” The Review of Economics and Statistics 78 (2): 214.
Belderbos, R., and L. Sleuwaegen.1998. “Tariff jumping DFI and export substitution: Japanese electronics firms in Europe.” International Journal of Industrial Organization 16 (5): 601–638.
Bemrose, R.K., W.M. Brown, and J. Tweedle. 2017. Going the Distance: Estimating the Effect of Provincial Borders on Trade when Geography Matters. Analytical Studies Branch Research Paper Series, no. 394. Statistics Canada Catalogue no. 11F0019M. Ottawa: Statistics Canada.
Bernard, A.B., A. Moxnes, and Y.U. Saito. 2015. Production Networks, Geography and Firm Performance. NBER Working Paper, no. 21082. Cambridge, Massachusetts: National Bureau of Economic Research.
Brainard, S.L. 1997. “An empirical assessment of the proximity-concentration trade-off between multinational sales and trade.” The American Economic Review 87 (4): 520–544.
Caves, R.E. 1996. Multinational Enterprise and Economic Analysis. Cambridge: Cambridge University Press.
Chaney, T. 2008. “Distorted gravity: the intensive and extensive margins of international trade.” The American Economic Review 98 (4): 1707–1721.
Chaney, T. 2014. “The network structure of international trade.” American Economic Review 104 (11): 3600–3634.
Chaundy, D. 2016. Trade Barriers in Atlantic Canada: Opportunities for Regulatory Reform. Halifax: Atlantic Provinces Economic Council.
Combes, P.P., M. Lafourcade, and T. Mayer. 2005. “The trade-creating effects of business and social networks: Evidence from France.” Journal of International Economics 66 (1): 1–29.
Duranton, G., and D. Puga. 2005. “From sectoral to functional urban specialisation.” Journal of Urban Economics 57 (2): 343–370.
Engel, C., and J.H. Rogers. 1996. “How Wide Is the Border?” The American Economic Review 86 (5): 1112–1125.
Garmendia, A., C. Llano, A. Minondo, and F. Requena. 2012. “Networks and the disappearance of the intranational home bias.” Economics Letters 116 (2): 178–182.
Head, K., and T. Mayer. 2014. “Gravity Equations: Workhorse, Toolkit, and Cookbook.” In Handbook of International Economics, ed. R.W. Jones, P.B. Kenen, G.M. Grossmann and K. Rogoff, Vol. 4, chapter 3, p. 131–195. Oxford, United Kingdom and Amsterdam: Elsevier.
Head, K., J. Ries, and B.J. Spencer. 2004. “Vertical Networks and US Auto Parts Exports: Is Japan Different?” Journal of Economics & Management Strategy 13 (604): 37–67.
Helliwell, J.F. 1998. How Much Do National Borders Matter? Washington, D.C.: The Brookings Institution.
Hillberry, R., and D. Hummels. 2008. “Trade responses to geographic frictions: A decomposition using micro-data.” European Economic Review 52 (3): 527–550.
Kindleberger, C.P. 1969. American Business Abroad: Six Lectures on Direct Investment. New Haven, Connecticut: Yale University Press. 225 p.
Lim, K. 2017. Firm-to-firm Trade in Sticky Production Networks. 2017 Annual Meeting of the Society for Economic Dynamics. Edinburgh, Scotland. June 22–24, 2017. Available at: https://economicdynamics.org/meetpapers/2017/paper_280.pdf (accessed May 2, 2018).
Nocke, V., and S. Yeaple. 2007. “Cross-border mergers and acquisitions vs. greenfield foreign direct investment: The role of firm heterogeneity.” Journal of International Economics 72 (2): 336–365.
Ramondo, N., V. Rappoport, and K.J. Ruhl. 2016. “Intra firm trade and vertical fragmentation in U.S. multinational corporations.” Journal of International Economics 98: 51–59.
Rauch, J. 1999. “Networks versus markets in international trade.” Journal of International Economics 48 (1): 7–35.
Rauch, J.E. 2001. “Business and Social Networks in International Trade.” Journal of Economic Literature 39 (4): 1177–1203.
Williamson, O.E. 1979. “Transaction-Cost Economics: The Governance of Contractual Relations.” The Journal of Law & Economics 22 (2): 233–261.
Williamson, O.E. 2008. “Outsourcing: Transaction cost economics and supply chain management.” Journal of Supply Chain Management 44 (2): 5–16.
Yeaple, S.R. 2013. “The Multinational Firm.” Annual Review of Economics 5 (1): 193–217.



