Analytical Studies Branch Research Paper Series
Accounting for Slower Productivity Growth in the Canadian Business Sector After 2000: Do Measurement Issues Matter?
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
by Wulong Gu
Skip to text
Text begins
Acknowledgements
An earlier version of the paper was presented to a productivity workshop in Ottawa in 2014 and the International Association for Research on Income and Wealth conference in 2016 in Dresden, Germany. The author would like to thank John Baldwin, Matt Krzepkowski, Danny Leung, Ryan Macdonald, Jean-Pierre Maynard, Marc Tanguay, Weimin Wang and Beiling Yan for their contributions to the analysis and research summarized in this paper. He would also like to thank Bert Balk, Erwin Diewert, Doug May, Khan Moore, Andrew Sharpe, Larry Shute, Rachel Soloveichik, Pierre St-Amant, and Jianmin Tang who have provided detailed comments and helpful suggestions.
Abstract
Labour productivity growth and multifactor productivity (MFP) growth slowed in Canada and other advanced economies after 2000. Several measurement challenges have been suggested as potential explanations for this trend. These include the measurement of intangible capital in a digital economy, the measurement of natural resource capital in the resource extraction sectors, the effect of infrastructure capital and the effect of cyclical fluctuations in the utilization of capital in industries adversely affected by world demand. This paper focuses on the role of these measurement issues in the slower productivity growth observed in Canada. It finds that measurement issues alone cannot explain the slowdown in productivity growth in Canada after 2000. Only 25% of the decline in MFP growth in the Canadian business sector in the period from 2000 to 2015, compared with the period from 1980 to 2000, is due to an increase in the use of produced capital and in the intermediate inputs required to extract natural resources with declining ore grades, and declining capital utilization in manufacturing. The decline in labour productivity and MFP growth is not due to changes in intangible capital and infrastructure capital after 2000.
Keywords: productivity, natural capital, intangible capital, capacity utilizationExecutive summary
Labour productivity growth and multifactor productivity (MFP) growth slowed in the Canadian business sector after 2000. Specifically, labour productivity growth declined from 1.7% per year in the period from 1980 to 2000 to 1.0% per year in the period from 2000 to 2015. MFP growth slowed from an increase of 0.4% per year in the first period to a decline of 0.2% per year in the second period. The recent slowdown in productivity growth also occurred in the United States and other developed economies.
Previous studies have identified a number of potential explanations for this trend. These include a slower pace of innovation and technological progress, a slowdown in the dissemination of innovation, a lack of competition, a decline in business dynamism, and a misallocation of resources because of a sharp decline in real interest rates. Several measurement challenges have also been suggested as potential explanations. These include the measurement of gross domestic product and knowledge capital in a digital economy, the measurement of natural resource capital in the resource extraction sectors, the effect of public infrastructure capital, and the effect of cyclical fluctuations in the utilization of capital.
This paper will focus on the role of measurement issues in accounting for slower productivity growth in the Canadian business sector after 2000.
First, the paper extends the asset coverage of the Canadian Productivity Accounts to include intangible capital, natural capital and public infrastructure capital so as to develop a more comprehensive measure of capital and better understand the contributions of these types of capital to labour productivity growth and to the decline in labour productivity growth in Canada after 2000. Intangible knowledge capital—such as innovation, human capital and organization capital―has been identified as an important source of output growth and productivity growth. However, growth accounting and the System of National Accounts generally do not include them as capital input. Natural capital is an important input to the mining and oil and gas extraction industry but is excluded from the measure of capital input to the industry. Public infrastructure capital contributes to the output and productivity growth of the business sector but is often not included in growth accounts.
Second, the paper examines the role that short-run changes in the utilization of capital input play in the slower manufacturing-industry MFP growth and the contribution of these changes to aggregate MFP growth in the business sector after 2000. Utilization of capital in Canadian manufacturing declined in the early 2000s, a period that was associated with slower export and output growth because of the appreciation of the Canadian dollar and slower growth in Canada’s largest trading partner, the United States.
The paper finds that measurement issues alone cannot explain the slowdown in productivity growth in the Canadian business sector after 2000. Only 25% of the decline in MFP growth in the Canadian business sector in the period from 2000 to 2015, compared with the period from 1980 to 2000, is due to an increase in the use of produced capital and in the intermediate inputs required to extract natural resources with declining ore grades, and declining capital utilization in manufacturing. The decline in labour productivity and MFP growth is not due to changes in intangible capital and infrastructure capital after 2000. Infrastructure capital contributed to an acceleration of labour productivity and MFP growth after 2000 as a result of a large increase in infrastructure investment in this period. The decline in MFP growth in the business sector was larger after 2000 when an adjustment is made for the effect of infrastructure and intangible capital.
1 Introduction
Labour productivity growth and multifactor productivity (MFP) growth slowed in the Canadian business sector after 2000 (Baldwin and Willox 2016; Almon and Tang 2011; Rao, Sharpe and Smith 2005).Note Specifically, labour productivity growth declined from 1.7% per year in the period from 1980 to 2000 to 1.0% per year in the period from 2000 to 2015. MFP growth slowed from an increase of 0.4% per year in the first period to a decline of 0.2% per year in the second period. The recent slowdown in productivity growth also occurred in the United States and other developed economies (Byrne, Fernald and Reinsdorf 2016; OECD 2015).
Previous studies have identified a number of potential explanations for this trend. These include a slower pace of innovation and technological progress, a slowdown in the dissemination of innovation, a lack of competition, a decline in business dynamism, and a misallocation of resources because of a sharp decline in real interest rates (Baily and Montalbano 2016; Cette, Fernald and Mojon 2016; OECD 2015; Sharpe and Murray 2017). Several measurement challenges have also been suggested as potential explanations. These include the measurement of gross domestic product and knowledge capital in a digital economy, the measurement of natural resource capital in the resource extraction sectors, the effect of public infrastructure capital, and the effect of cyclical fluctuations in the utilization of capital (Ahmad and Schreyer 2016; Byrne, Fernald and Reinsdorf 2016; Rao, Sharpe and Smith 2005).
This paper focuses on the role of measurement issues in accounting for slower productivity growth in the Canadian business sector after 2000.
First, the paper extends the asset coverage of the Canadian Productivity Accounts (CPA) to include intangible capital, natural capital and public infrastructure capital so as to develop a more comprehensive measure of capital and better understand the role of investment in output and labour productivity growth. Intangible knowledge capital—such as innovation, human capital and organization capital—has been identified as an important source of output growth and productivity growth. However, growth accounting and the System of National Accounts (SNA) generally do not include them in the value of output or the value of capital input. Natural capital is an important input to the mining and oil and gas extraction industry but is excluded from the measure of capital input to the industry. Public infrastructure capital contributes to the output and productivity growth of the business sector but is often not included in growth accounts.
While expanding the asset coverage to include intangible capital, natural capital and public capital will affect MFP growth, the extent to which this capital accounts for the decline in labour productivity and MFP growth is not known. This paper will examine the changes in these types of capital after 2000 and whether these changes explain slower labour productivity and MFP growth after 2000.
Second, the paper will focus on the role that short-run changes in the utilization of capital input play in the slower MFP growth in Canadian manufacturing after 2000. Utilization of capital in this industry declined in the early 2000s, a period that was associated with slower export and output growth because of the appreciation of the Canadian dollar and slower growth in Canada’s largest trading partner, the United States. The decline in MFP growth after 2000 was found to be partly due to this decline in the utilization of capital in this period (Baldwin, Gu and Yan 2013).
While previous studies have used various procedures to examine the effect of changes in capacity utilization on MFP growth, the procedures are often ad hoc. To address this gap, a new measure of capacity utilization has been developed; it can be used to adjust MFP growth for changes in the utilization of capital input (Gu and Wang 2013).
The methodologies that can be used to address these measurement challenges were established in previous studies from Canada and other countries. The contribution of this paper is to use these methodologies to extend the estimates to more recent years and to ask to what extent these measurement issues account for the slower labour productivity and MFP growth in Canada after 2000.
In addition to the measurement issues examined in this paper, issues associated with the measurement of service-sector output, the measurement of output from new goods and services, and the measurement of the price of information and communication equipment could be important in explaining slower productivity growth in recent years. However, it is not clear that these measurement issues have become more pronounced in recent years, thereby contributing to the recent productivity growth slowdown. The measurement of “free” digital services (e.g., social media and search engines) is also mentioned as a factor in slower productivity growth (Varian 2011; Brynjolfsson and Oh 2012; Nakamura, Samuels and Soloveichik 2016). Output and productivity growth, if extended to include the benefit of digital services, would have increased faster in recent years. But this benefit is the output of non-market production and is outside the production boundary of the SNA.
The rest of the paper is organized as follows. Section 2 begins with a decomposition of MFP growth into the contributions of industries to identify the industries responsible for the slower MFP growth in the Canadian business sector after 2000. Identifying these industries sheds light on potential measurement issues that affect them. The section will provide a modified Domar decomposition of aggregate MFP into industry contributions when the sum of input costs differs from the value of output. Section 3 extends the asset coverage to include intangible capital, infrastructure capital and natural capital. Section 4 takes into account changes in capacity utilization in MFP growth in manufacturing. Section 5 presents the role these measurement issues play in the slower productivity growth in the Canadian business sector after 2000. Section 6 concludes the paper.
2 Aggregate and industry productivity growth in Canada
This section summarizes the trend in productivity growth at the aggregate business-sector level and traces aggregate MFP growth back to the contributions of individual industries. It focuses on the industries that are sources of the decline in aggregate MFP growth after 2000. The data are taken from the CPA of Statistics Canada.
The CPA follow the framework laid down by Jorgenson (1966); Jorgenson, Gollop and Fraumeni (1987); Jorgenson, Ho and Stiroh (2005); and Schreyer (2001). They developed integrated industry and total economy growth accounts.Note In their accounts, industry-level productivity growth is estimated using detailed data on output and inputs, and aggregate productivity growth is estimated using industry-level data. Industry productivity accounts and aggregate productivity accounts are fully integrated; MFP growth at the aggregate level and MFP growth at the industry level are related to one another through Domar aggregation (Domar 1961).
MFP growth in the CPA is defined as output growth that is not accounted for by the growth of capital, labour and intermediate inputs. To estimate MFP growth, the user cost and volume index of capital input are estimated first. The user cost of capital is equal to the sum of the rate of return to capital, depreciation and capital gains adjusted for the effects of tax treatments. The rate of return can be set either to the endogenous rate of return or to the exogenous rate of return (Diewert and Yu 2012). Prior to the 2013 revision (as documented by Baldwin et al. [2014]), the endogenous (or internal) rate of return method was used in Canada, where the rate of return is estimated from the assumption that the user cost of capital across assets is equal to capital income. In this approach, the sum of input costs exhausts the value of output. The approach is based on the assumption that there is perfect competition and constant returns to scale. It gives rise to the Domar aggregation: aggregate MFP growth is a weighted sum of industry MFP growth where weights are equal to the share of an industry in aggregate nominal output (Domar 1961).
To address the volatility of internal rates of return that often occurs at the industry level (Diewert and Yu 2012; Harper, Nakamura and Zhang 2012), Statistics Canada’s Multifactor Productivity Program adopted a variant of the endogenous approach in 2013 (Baldwin et al. 2014). The external rates of return are now used to estimate the user cost of capital for industries with extremely high and low internal rates of return.Note In addition, for a number of service industries where internal rates of return are unusually high and exhibit unusual trends, capital input is imputed by dividing gross operating surplus by the user cost of capital estimated using the external rates of return.Note
This approach to estimating capital input provides an estimation of a surplus: the difference between capital income from the SNA and capital costs. This difference could be the result of imperfect competition. It could also arise because the list of inputs included in the MFP estimates is incomplete (e.g., many intangibles are excluded). Or it could arise because of economies of scale, so that paying inputs their marginal revenue product does not completely exhaust the value of output. As a result of the surplus, the Domar aggregation needs to be modified. The remainder of this section first develops a modified Domar aggregation that relates industry MFP growth to aggregate MFP growth in the presence of a surplus. It then uses the aggregation to decompose MFP growth in the aggregate business sector into the contributions of individual industries.Note
2.1 Modified Domar decomposition
2.1.1 Industry productivity measure
An integrated productivity account starts with the measurement of MFP at the industry level. Industry i is characterized by a production function that expresses gross output as a function of capital , labour , intermediate input and technology :
The nominal value of gross output for industry i is equal to the sum of capital, labour and intermediate input costs plus a surplus:
where and are the prices of gross output, capital input, labour input and intermediate input. is surplus or profits. As in standard growth accounting, the price of gross output is valued at basic prices, and the prices of inputs are valued at purchaser prices.
When there is a surplus, MFP growth based on gross output ( ) can be written as the difference between output growth and the cost-weighted input growth (Hall 1990):
where , , and are the shares of capital, labour and intermediate inputs in the sum of capital, labour and intermediate input costs. is the log difference or log growth of a variable between two periods. are the shares of capital costs, labour costs, intermediate input costs and surplus in the nominal value of gross output in industry . The sum of those shares in gross output equals 1.
Equation (3) was developed by Hall (1990), who showed that aggregate input growth should be cost-weighted for measuring MFP growth when there is imperfect competition and increasing returns to scale. In general, Balk (2010) and Schreyer (2010) showed that cost-weighted input growth is the preferred measure for calculating MFP growth when there is a surplus, regardless of the sources of the surplus.
MFP growth in Equation (3) is based on gross output. Alternatively, MFP growth can be estimated using value-added output. MFP growth based on value added ( ) can be defined as the difference between the growth of value added and the growth of cost-weighted capital and labour inputs, with weight being given by the share of capital and labour input costs in the sum of capital and labour costs:
Value-added MFP growth in Equation (4) is related to gross output MFP growth in Equation (3). To see this, note that value added in current dollars is calculated as the difference between the value of gross output and the value of intermediate inputs. Value added in constant dollars (A) can be calculated from the equation that expresses gross output as a Törnqvist aggregation of value added and intermediate inputs:Note
The equation can be rewritten to express value added in constant dollars as a difference between a share-weighted gross output in constant dollars and a share-weighted intermediate input in constant dollars:
This method is called double deflation. Substituting from Equation (6) in Equation (4) yields the following equation that relates MFP growth based on value added to MFP growth based on gross output:Note
Value-added MFP growth is equal to gross-output MFP growth times the ratio of the sum of capital, labour and intermediate input costs to the sum of capital and labour input costs, plus a term that reflects the effect of changes in vertical integration on MFP growth. The term is positive if the growth of intermediate inputs exceeds the growth of real value added.Note
If there is no surplus, the equation is simplified to the well-known relationship between value-added MFP growth and gross-output MFP growth. Value-added MFP growth is equal to gross-output MFP growth times the ratio of nominal gross output to nominal value added (Bruno 1978; Jorgenson, Ho and Stiroh 2005).Note
2.1.2 Aggregate productivity measure
Aggregate MFP growth in the total business sector is constructed from industry productivity accounts using the bottom-up approach. Specifically, value-added growth in the total business sector is derived from an aggregation of industry value-added growth using the industry share of nominal value added as weights. Aggregate capital input growth is derived from an aggregation of industry capital input growth using the industry share of capital costs as weights. However, aggregate labour input is derived from an aggregation of different types of hours worked, cross-classified by education levels, experience and employment types at the aggregate level. This is done so the methodology in the Canadian MFP program is comparable with the one adopted by the Bureau of Labor Statistics for the United States.Note
MFP growth in the total business sector is estimated as the difference between the growth of aggregate value added and the growth of combined aggregate capital input and aggregate labour inputs.
When aggregate MFP growth is constructed using the bottom-up approach, aggregate MFP growth of value added is equal to a weighted sum of industry MFP growth using the industry shares of capital and labour costs as weights, plus a term that reflects the deviation of the output value from input costs or the presence of a surplus:
where is aggregate MFP growth based on value-added output, is the share of industry in the sum of capital and labour costs in the total business sector, and is the share of industry in the nominal value added of the total business sector.
The second term measures the effect of the reallocation of value added across industries. The term is negative when industries with a smaller surplus or lower markup (such as service sectors) have faster output growth than industries with a larger surplus or higher markup. If there is no surplus, the aggregation becomes a standard Domar aggregation: aggregate MFP growth is a weighted sum of industry MFP growth.
Balk (2015) referred to the second term as the price effect. It is a result of imperfect competition, the presence of a surplus and the method that the SNA use to derive aggregate value-added growth. When there is imperfect competition, aggregate value-added growth should be calculated as a weighted sum of value-added growth across industries using industry shares of total costs as weights. When this is done, the second term in Equation (8) is 0 and aggregate MFP is equal to a weighted sum of industry MFP growth using industry shares of total costs as weights. But in the SNA, aggregate value-added growth is calculated using industry shares of aggregate value added as weights, which assumes perfect competition. As a result, aggregate MFP growth is equal to a weighted sum of industry MFP growth plus a reallocation term, as shown in Equation (8).
Substituting Equation (7) for in Equation (8) creates an equation that expresses aggregate value-added MFP growth as an aggregation of gross-output MFP growth across industries:
Aggregate MFP growth from the bottom-up approach is decomposed into three components. The first component is a weighted sum of gross-output MFP growth across industries. The weight for an industry is the ratio of the sum of capital, labour and intermediate costs in an industry to the sum of capital and labour costs at the aggregate level. The sum of the weights exceeds 1. The second and third components arise as a result of imperfect competition and surplus. They represent the effect of changes in intermediate input intensities and the effect of reallocation of value added across industries. When there is perfect competition and no surplus, the aggregation becomes a standard Domar aggregation, and the second and third terms in the equation are equal to 0.
The modified Domar decomposition in Equations (8) and (9) calculates industry contributions using industry shares of input costs. In contrast, the standard Domar decomposition uses industry shares of nominal output, which would overstate the contribution of industries with a positive surplus, as their share in nominal output exceeds their share in total input costs. It would understate the contributions of industries with a negative surplus.
The modified Domar decomposition also raises the issue of the interpretation of aggregate MFP growth constructed using the bottom-up approach and an external rate of return for calculating capital input. As shown in Equations (8) and (9), aggregate MFP growth reflects productivity growth in an industry that captures the effect of innovation, scale economics and business practices on production in the industry. It also captures the effect of the reallocation of output across industries with a large surplus. As a large surplus implies that the value of the output to consumers exceeds the costs of production, this reallocation is more closely associated with welfare improvement (Hulten and Schreyer 2010) rather than productivity growth.
2.2 Aggregate productivity growth in the total business sector
Table 1 presents the trend in output and productivity growth in the total business sector. The first three rows in the table decompose output growth into the contribution from growth in hours worked and the contribution from growth in labour productivity. The last three rows decompose labour productivity growth into contributions of capital deepening, changes in labour composition, and MFP growth.
| 1980 to 2000 | 2000 to 2015 | 2000 to 2015 less 1980 to 2000 |
|
|---|---|---|---|
| percent | |||
| Growth in real value-added | 3.2 | 1.8 | -1.4 |
| Growth in hours worked | 1.5 | 0.9 | -0.6 |
| Labour productivity growth | 1.7 | 1.0 | -0.7 |
| Contributions to labour productivity growth from | |||
| Capital deepening | 0.9 | 0.9 | 0.0 |
| Labour composition | 0.4 | 0.2 | -0.2 |
| MFP growth | 0.4 | -0.2 | -0.6 |
| Note: MFP: multifactor productivity. Source: Statistics Canada, author’s calculation based on data from Table 36-10-0208-01. |
|||
Output growth declined in the total business sector during the period from 2000 to 2015, compared with the period from 1980 to 2000. Specifically, it declined from 3.2% per year to 1.8% per year. The decline in output growth after 2000 reflects both a decline in labour productivity growth and a decline in the growth of hours worked.
Labour productivity growth declined from 1.7% per year over the period from 1980 to 2000 to 1.0% per year over the period from 2000 to 2015. This 0.7-percentage-point decline after 2000 was almost entirely due to a decline in MFP growth after 2000. MFP growth declined from an increase of 0.4% per year in the period from 1980 to 2000 to a decrease of 0.2% per year in the period from 2000 to 2015. There is little change in the contribution of capital deepening effects. Labour compositional effects declined from 0.4% to 0.2% between these two periods.
2.3 Industry contributions to multifactor productivity growth
This section quantifies the contributions of industries to the decline in MFP growth in the total business sector after 2000. Table 2 and Chart 1 present MFP growth based on value added by industry. Table 3 presents the industry contributions to aggregate MFP growth. As shown in Section 2.1, the contribution of an industry to aggregate MFP growth is equal to the industry’s MFP growth multiplied by the share of the industry in the sum of aggregate capital and labour input costs.
| 1980 to 2000 | 2000 to 2015 | 2000 to 2015 less 1980 to 2000 |
|
|---|---|---|---|
| percent | |||
| Industry | |||
| Agriculture, forestry, fishing and hunting | 2.7 | 2.5 | -0.2 |
| Mining and oil and gas extraction | -0.3 | -4.6 | -4.3 |
| Utilities | 0.3 | -1.4 | -1.7 |
| Construction | -0.3 | -0.3 | 0.0 |
| Manufacturing | 2.1 | 0.3 | -1.8 |
| Wholesale trade | 2.1 | 1.5 | -0.6 |
| Retail trade | 1.1 | 1.1 | 0.0 |
| Transportation and warehousing | 1.2 | -0.3 | -1.5 |
| Information and cultural industries | 0.4 | 0.7 | 0.3 |
| Finance, insurance, real estate and renting and leasing | -0.7 | 1.0 | 1.7 |
| Professional, scientific and technical services | -1.1 | -0.3 | 0.8 |
| Administrative and support, waste management and remediation services | -1.5 | -0.7 | 0.8 |
| Arts, entertainment and recreation | -3.2 | -1.1 | 2.1 |
| Accommodation and food services | -1.3 | 0.1 | 1.4 |
| Other private services | -0.9 | 0.1 | 1.0 |
| Total business sector | 0.4 | -0.2 | -0.6 |
| Note: Multifactor productivity growth is based on value added. Source: Statistics Canada, author’s calculation based on data from Table 36-10-0208-01. |
|||

Data table for Chart 1
| Industries | 1980 to 2000 | 2000 to 2015 |
|---|---|---|
| percent per year | ||
| Agriculture, forestry, fishing and hunting | 2.745 | 2.480 |
| Mining and oil and gas extraction | -0.292 | -4.563 |
| Utilities | 0.334 | -1.431 |
| Construction | -0.332 | -0.261 |
| Manufacturing | 2.123 | 0.311 |
| Wholesale trade | 2.145 | 1.465 |
| Retail trade | 1.142 | 1.060 |
| Transportation and warehousing | 1.208 | -0.262 |
| Information and cultural industries | 0.429 | 0.707 |
| Finance, insurance, real estate and renting and leasing | -0.749 | 0.968 |
| Professional, scientific and technical services | -1.060 | -0.256 |
| Administrative and support, waste management and remediation services |
-1.540 | -0.737 |
| Arts, entertainment and recreation | -3.224 | -1.091 |
| Accommodation and food services | -1.314 | 0.119 |
| Other private services | -0.884 | 0.060 |
| Total business sector | 0.430 | -0.181 |
|
Source: Statistics Canada, author's calculations based on data from Table 36-10-0208-01. |
||
| 1980 to 2000 | 2000 to 2015 | 2000 to 2015 less 1980 to 2000 |
|
|---|---|---|---|
| percent | |||
| Industry | |||
| Agriculture, forestry, fishing and hunting | 0.09 | 0.06 | -0.03 |
| Mining and oil and gas extraction | -0.03 | -0.43 | -0.40 |
| Utilities | 0.01 | -0.05 | -0.06 |
| Construction | -0.03 | -0.02 | 0.01 |
| Manufacturing | 0.50 | 0.06 | -0.44 |
| Wholesale trade | 0.14 | 0.10 | -0.04 |
| Retail trade | 0.08 | 0.07 | -0.01 |
| Transportation and warehousing | 0.09 | -0.02 | -0.11 |
| Information and cultural industries | 0.02 | 0.03 | 0.01 |
| Finance, insurance, real estate and renting and leasing | -0.10 | 0.15 | 0.25 |
| Professional, scientific and technical services | -0.05 | -0.02 | 0.03 |
| Administrative and support, waste management and remediation services | -0.03 | -0.02 | 0.01 |
| Arts, entertainment and recreation | -0.02 | -0.01 | 0.01 |
| Accommodation and food services | -0.04 | 0.00 | 0.04 |
| Other private services | -0.04 | 0.00 | 0.04 |
| Sum of industry contributions | 0.61 | -0.09 | -0.70 |
| Reallocation of output | -0.18 | -0.09 | 0.09 |
| Total business sector | 0.43 | -0.18 | -0.61 |
| Source: Statistics Canada, author’s calculation based on data from Table 36-10-0208-01. | |||
In the period before 2000, the industries that experienced high MFP growth were agriculture, forestry, fishing and hunting; manufacturing; wholesale trade; retail trade; and transportation and warehousing. These industries accounted for almost all MFP growth in the total business sector for that period. The high MFP growth in these industries is a result of their innovation and technical progress. For example, the rapid MFP growth in the manufacturing industry was a result of a trend towards trade liberalization in manufacturing that led to innovation and the adoption of advanced manufacturing technologies.
In the period after 2000, MFP growth slowed or became negative in goods-producing industries, especially in mining and oil and gas extraction, and in manufacturing. The service industries that invested heavily in information and communication technologies maintained positive MFP growth and, in general, did not show a decline in MFP growth after 2000. These service industries include wholesale trade; retail trade; information and cultural industries; and finance, insurance, real estate and renting and leasing.
MFP increased 0.4% per year in the business sector over the period from 1980 to 2000. It then declined by 0.2% per year over the period from 2000 to 2015. This represents a 0.6-percentage-point decline in MFP growth between the two periods. This decline in aggregate MFP growth after 2000 was mostly due to a decline in MFP in two industries: manufacturing, and mining and oil and gas extraction. The decline in MFP growth in the manufacturing industry accounted for a 0.4-percentage-point decline in aggregate MFP growth. The decline in MFP growth in the mining and oil and gas extraction industry accounted for another 0.4-percentage-point decline in aggregate MFP growth after 2000.
The sum of industry contributions differs from aggregate MFP growth in the total business sector. The difference reflects the effect of reallocation in value added on aggregate MFP growth. The effect of the reallocation is found to be negative for all periods. This is a result of a negative correlation between surplus and output growth: the industries with a smaller or negative surplus tend to grow faster, as shown in Table 4. Transportation and warehousing, and information and cultural industries, with a large negative surplus, experienced rapid growth in output over the period from 1961 to 2013. Accommodation and food services, and other private services, with a large positive surplus, experienced relatively slower growth. However, there are exceptions to this negative correlation between surplus and output growth for professional, scientific and technical services; and administrative and support, waste management and remediation services. These industries had a large positive surplus while experiencing faster growth in output.
| Share of surplus | Value-added growth | |
|---|---|---|
| percent | ||
| Industry | ||
| Agriculture, forestry, fishing and hunting | -0.1 | 1.9 |
| Mining and oil and gas extraction | -1.6 | 1.9 |
| Utilities | 0.1 | 1.3 |
| Construction | 16.8 | 2.0 |
| Manufacturing | 3.8 | 1.5 |
| Wholesale trade | 0.0 | 4.4 |
| Retail trade | 0.0 | 3.3 |
| Transportation and warehousing | -29.8 | 3.0 |
| Information and cultural industries | -10.4 | 3.6 |
| Finance, insurance, real estate and renting and leasing | 0.3 | 3.3 |
| Professional, scientific and technical services | 11.9 | 4.1 |
| Administrative and support, waste management and remediation services | 14.2 | 4.1 |
| Arts, entertainment and recreation | -0.2 | 2.2 |
| Accommodation and food services | 11.6 | 1.3 |
| Other private services | 12.1 | 2.3 |
| Total business sector | 2.2 | 2.6 |
| Note: The share of surplus is the share of surplus in nominal value added averaged over the period from 1980 to 2013. Source: Statistics Canada, author’s calculation based on data from Table 36-10-0208-01. |
||
When there is a surplus, the correct weights for estimating industry contributions to aggregate MFP growth are based on input costs. If the weights are based on the value of output, the estimated contributions will be biased. But the bias has been found to be small in Canada, because industry contributions estimated using output shares are similar to the contributions based on input cost shares.
The finding that the manufacturing industry and the mining and oil and gas extraction industry are largely responsible for the decline in aggregate MFP growth after 2000 warrants a further investigation of potential issues in these industries. These issues include the decline in the utilization of capital in manufacturing, and the incorporation of natural capital input in the measurement of MFP growth in mining and oil and gas extraction.
3 Role of intangible capital, natural capital and infrastructure capital in labour productivity growth
This section extends the asset coverage in the CPA to include natural capital, intangible capital and infrastructure capital so as to provide a more comprehensive measure of capital input and examine the contributions of these types of capital to output and labour productivity growth and to the decline in labour productivity growth after 2000.
3.1 Intangible capital and multifactor productivity growth in the business sector
The accuracy of MFP estimates depends on the comprehensiveness of and the measurement in the SNA that feed the Multifactor Productivity Program. Recent attention has been paid to the incomplete coverage of assets used for estimating capital input. In particular, it has been argued that a number of intangible assets have not been appropriately taken into account in measuring the growth in capital. Intangible assets include computerized information (software and computerized databases), innovative property (scientific research and development [R&D] and non-scientific R&D) and economic competencies (brand equity, training and organizational capital) (Corrado, Hulten and Sichel 2009). The MFP measure published by Statistics Canada and others includes only a small portion of intangible assets those related to R&D, exploration and software. Whether the inadequate coverage of intangibles has a negative effect on the MFP measure is difficult to judge without an empirical study, since reclassifying an intermediate expense to an investment affects both measured output and measured capital.
Baldwin et al. (2009) and Baldwin, Gu and Macdonald (2012) developed a more extensive measure of intangible capital than is used at present in the SNA and extended the growth accounting to include intangible capital. They found that investment in intangibles totalled $151 billion in the Canadian business sector in 2008, representing 13.2% of gross domestic product in that year. Investment in intangibles increased much faster over time than investment in tangibles, and the ratio of intangible investment to tangible investment increased from 0.23 in 1976 to 0.66 in 2008. Their results are updated in Table 5, which shows that intangibles made a significant contribution to labour productivity growth in the Canadian business sector. The contribution of intangibles to labour productivity growth was 0.4 percentage points or 40% of the total capital deepening effect in the period 1980 to 2000, and 0.2 percentage points or 25% of the total capital deepening effect in the period 2000 to 2015 (Table 5).
| 1980 to 2000 | 2000 to 2015 | 2000 to 2015 less 1980 to 2000 |
|
|---|---|---|---|
| percent | |||
| Including SNA intangibles | |||
| Labour productivity growth | 1.70 | 0.95 | -0.75 |
| Contributions | |||
| Capital deepening | 0.89 | 0.90 | 0.01 |
| Labour composition | 0.38 | 0.23 | -0.15 |
| Multifactor productivity growth | 0.43 | -0.18 | -0.61 |
| Including all intangibles | |||
| Labour productivity growth | 1.82 | 0.97 | -0.85 |
| Contributions | |||
| Capital deepening | 0.91 | 0.95 | 0.04 |
| Tangible | 0.53 | 0.71 | 0.18 |
| Intangible | 0.38 | 0.24 | -0.14 |
| Labour composition | 0.35 | 0.21 | -0.14 |
| Multifactor productivity growth | 0.56 | -0.19 | -0.75 |
| Note: SNA: System of National Accounts. Source: term@stat and OECD (Organization of Economic Development and Cooperation). J.R. Baldwin, W. Gu, and R. Macdonald, 2012, Intangible Capital and Productivity Growth in Canada, Table 3. |
|||
When expenditures on intangibles are reclassified as investment from intermediate inputs and added to value added in the business sector, the adjusted real value added and labour productivity growth were higher in the periods from 1980 to 2000 and from 2000 to 2015. This is because expenditures on intangibles increased faster than value added in these two periods.
The adjustment to output and labour productivity growth was larger in the period from 1980 to 2000 than in the period after 2000. As a result, incorporating intangibles made the decline in aggregate labour productivity growth after 2000 even larger. In other words, changes in intangible investment between the two periods do not explain the decline in aggregate labour productivity growth after 2000.
Expanding the asset coverage to include intangible capital also affects MFP growth in the business sector. For the period 1980 to 2000, it had little effect on the capital deepening effect and increased MFP growth. For the period 2000 to 2015, the effect of including intangibles is to increase the capital deepening effect and reduce the MFP growth. Therefore, the decline in MFP growth after 2000 was larger when intangibles were included in capital input.
3.2 Natural capital and multifactor productivity growth in mining and oil and gas extraction
MFP has been declining in the oil and gas extraction subsector since the early 1990s, and has been declining in the mining subsector (coal, metal ore and non-metallic mineral mining) since the early 2000s (Chart 2).Note The decline in MFP in these two subsectors accounted for a 0.4-percentage-point decline in MFP growth in the total business sector after 2000 (Table 3).
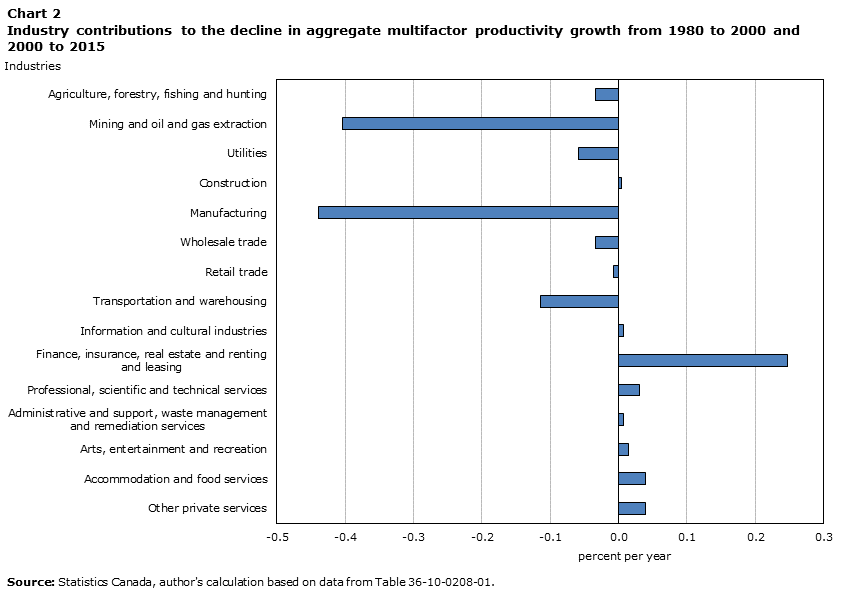
Data table for Chart 2
| Industries | 2000 to 2015 minus 1980 to 2000 |
|---|---|
| percent per year | |
| Agriculture, forestry, fishing and hunting | -0.034 |
| Mining and oil and gas extraction | -0.403 |
| Utilities | -0.058 |
| Construction | 0.005 |
| Manufacturing | -0.439 |
| Wholesale trade | -0.034 |
| Retail trade | -0.007 |
| Transportation and warehousing | -0.114 |
| Information and cultural industries | 0.008 |
| Finance, insurance, real estate and renting and leasing |
0.247 |
| Professional, scientific and technical services | 0.031 |
| Administrative and support, waste management and remediation services |
0.008 |
| Arts, entertainment and recreation | 0.014 |
| Accommodation and food services | 0.039 |
| Other private services | 0.040 |
| Source: Statistics Canada, author's calculation based on data from Table 36-10-0208-01. | |
The decline in MFP in the mining and oil and gas extraction industry does not necessarily suggest there is a decline in technical efficiency. It may reflect the decline in the quality of ore bodies and oil and gas deposits and an increase in the difficulties of extracting these natural resources.
The existing MFP measure does not take into account the depletion of natural resource stock or the flow of natural capital input. When natural capital is not included in capital input, the MFP measure is biased, as the output includes the rent, while the input does not include the flow of natural resource capital (or natural capital input) used to generate that output (Schreyer 2012; Olewiler 2017). Research in Australia and the Netherlands shows that a substantial part of the decline in MFP in the mining and oil and gas exploitation industry can be attributed to unmeasured natural capital input (Topps and Kuluys 2014; Veldhuizen and de Haan 2012; ABS 2014).Note The resource extraction sectors in these countries involve more and more physical capital being applied to the extraction of natural resources because they are increasingly difficult to extract. The growth in physical capital input is higher than the growth in natural capital input, and the growth of a capital input estimate that includes both natural capital and physical capital will be slower than the growth in physical capital alone. Therefore, MFP growth is higher when the depletion of natural resource stock is taken into account in Australia and the Netherlands.
Schreyer (2012) presented an extended growth accounting framework for incorporating natural capital input in the MFP measure for the mining and oil and gas extraction industry. In the extended framework, the volume index of natural capital input is equal to the volume index of resource extraction, while the user cost of natural capital input is the resource rent. The resource rent can be estimated residually and is equal to the difference between the value of the resource extracted and the costs of capital other than natural capital calculated using an exogenous rate of return.Note
This procedure for estimating the volume index of natural capital input differs from that for estimating the volume index of the other capital. The volume index of capital input other than natural capital is not observed and is assumed to be proportional to capital stock. In contrast, the volume index of natural capital input is observed and is equal to the volume of resource extraction.
An industry often uses various natural capital inputs such as coal, metal ores and non-metallic minerals in its production. These different types of natural capital inputs need to be aggregated to derive an aggregate measure of natural capital input. Similar to the procedure for aggregating produced capital across asset types, the weights for the aggregation should be based on the user costs of natural capital inputs. Adams and Wang (2015) implemented such an approach using resource rent estimates for various types of natural capital inputs within an industry.
The resource rents by asset are often difficult to estimate as revenues and input costs must be allocated between multiple resources for the firms that engage in the extraction of multiple natural resource assets. For this paper, the value of natural resource assets will be used for aggregation. This assumes that resource rent per dollar value of resources extracted is equalized across different types of resource assets. This is the procedure used by Statistics Netherlands in its measure of natural capital input and MFP for the mining sector (Veldhuizen and de Haan 2012). In Canada, the choice of weights for aggregation has been found to have little effect on growth in estimated natural capital input.
Table 6 and Chart 3 present the extended growth accounts for the oil and gas extraction and the mining subsectors. The data on gross output, capital, labour and intermediate inputs are taken from the CPA of Statistics Canada (Table 36-10-0217-01 formerly CANSIM table 383-0032). The volume index of natural capital input is derived from the “make” tables of input output accounts and is available up to the most recent input output table reference year, namely 2013.
| 1980 to 2000 | 2000 to 2013 | |
|---|---|---|
| percent | ||
| Real gross output | 3.7 | 2.4 |
| Contributions | ||
| Labour input | 0.1 | 0.5 |
| Capital input | 1.6 | 3.0 |
| Natural capital input | 0.4 | 0.1 |
| Intermediate input | 1.8 | 1.6 |
| MFP growth | -0.2 | -2.8 |
| Addendum | ||
| Real output growth | 3.7 | 2.4 |
| Labour input growth | 2.4 | 7.6 |
| Capital input growth | 3.9 | 6.7 |
| Natural capital input growth | 3.4 | 2.3 |
| Intermediate input growth | 4.8 | 4.6 |
| MFP growth without natural capital | -0.7 | -3.6 |
| Note: MFP: multifactor productivity. Source: Statistics Canada, author’s calculation based on data from Table 36-10-0217-01 and the supply and use tables from the Industry Accounts Division of Statistics Canada. |
||
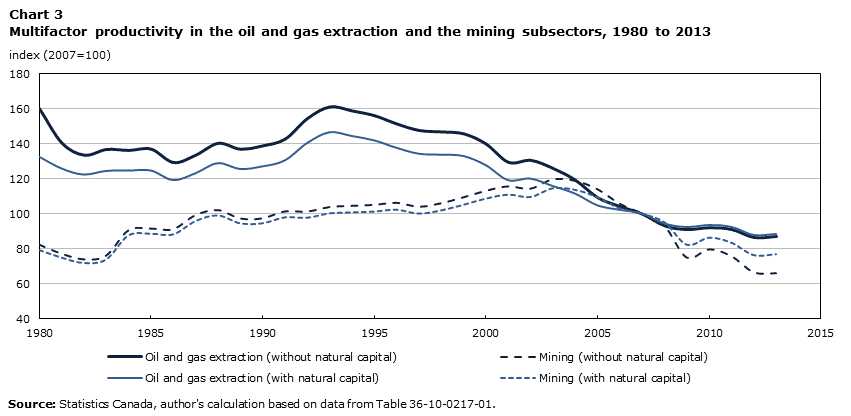
Data table for Chart 3
| Oil and gas extraction (without natural capital) | Mining (without natural capital) | Oil and gas extraction (with natural capital) | Mining (with natural capital) | |
|---|---|---|---|---|
| index (2007=100) | ||||
| 1980 | 160.186 | 82.368 | 132.492 | 79.107 |
| 1981 | 140.592 | 77.223 | 125.781 | 74.754 |
| 1982 | 133.658 | 73.981 | 122.283 | 71.651 |
| 1983 | 136.914 | 76.089 | 124.383 | 73.632 |
| 1984 | 136.396 | 90.482 | 124.541 | 87.513 |
| 1985 | 137.110 | 91.481 | 124.627 | 88.490 |
| 1986 | 129.455 | 91.148 | 119.145 | 88.114 |
| 1987 | 133.714 | 99.078 | 123.046 | 95.727 |
| 1988 | 140.425 | 101.986 | 128.803 | 99.005 |
| 1989 | 137.084 | 97.280 | 125.505 | 94.489 |
| 1990 | 139.003 | 97.310 | 126.962 | 94.480 |
| 1991 | 142.847 | 101.273 | 130.347 | 97.891 |
| 1992 | 154.564 | 101.132 | 140.280 | 97.699 |
| 1993 | 161.211 | 103.739 | 146.417 | 100.190 |
| 1994 | 158.924 | 104.431 | 144.307 | 100.752 |
| 1995 | 156.211 | 104.991 | 141.837 | 101.242 |
| 1996 | 151.473 | 106.178 | 137.563 | 102.275 |
| 1997 | 147.759 | 103.921 | 134.208 | 100.074 |
| 1998 | 146.954 | 105.883 | 133.653 | 101.882 |
| 1999 | 145.825 | 109.286 | 132.860 | 105.127 |
| 2000 | 139.982 | 112.940 | 127.654 | 108.686 |
| 2001 | 129.585 | 115.504 | 119.072 | 110.958 |
| 2002 | 130.696 | 114.205 | 119.977 | 109.624 |
| 2003 | 126.090 | 119.445 | 115.727 | 114.606 |
| 2004 | 119.342 | 118.652 | 111.416 | 113.727 |
| 2005 | 109.339 | 113.869 | 104.714 | 109.487 |
| 2006 | 104.332 | 105.586 | 102.181 | 103.015 |
| 2007 | 100.000 | 100.000 | 100.000 | 100.000 |
| 2008 | 93.296 | 93.049 | 94.300 | 95.017 |
| 2009 | 91.245 | 75.036 | 92.334 | 82.163 |
| 2010 | 92.281 | 79.669 | 93.493 | 86.208 |
| 2011 | 91.247 | 75.755 | 92.393 | 83.261 |
| 2012 | 86.705 | 66.631 | 87.794 | 76.135 |
| 2013 | 87.270 | 66.071 | 88.366 | 76.671 |
| Source: Statistics Canada, author's calculation based on data from Table 36-10-0217-01. | ||||
The growth in produced capital, inventory capital, and labour and intermediate inputs was faster than the growth in natural capital input in the Canadian oil and gas extraction subsector from 1980 to 2013. The difference becomes larger after 2000. This reflects an increased use of traditional natural capital input for extraction in the oil and gas extraction subsector, as oil and gas become increasingly expensive to extract.
The extended growth accounts for oil and gas extraction in Table 6 also provide an assessment of the contribution of natural capital input to economic growth. From 1980 to 2013, the largest contributors to output growth in the oil and gas extraction subsector are the other capital and intermediate inputs, followed by natural capital input and labour input. Natural capital input contributed 0.4 percentage points to the 3.7% annual growth in gross output in oil and gas extraction from 1980 to 2000, and contributed 0.1 percentage point to the 2.4% annual growth in gross output from 2000 to 2013.
MFP growth without natural capital decreased in the oil and gas extraction subsector in the 1980- to-2000 and 2000-to-2013 periods. But the decline was much larger after 2000. It declined 0.7% per year in the period from 1980 to 2000, and fell 3.6% per year in the period from 2000 to 2013. This translates into a 2.9-percentage-point slowdown in MFP growth in the oil and gas extraction subsector over the two periods. If natural capital is included in the measurement of capital, the decline in MFP is smaller in both periods, as is the slowdown in MFP growth after 2000. The decline in MFP and the slowdown in MFP growth after 2000 in the oil and gas extraction subsector are found to be partly due to unmeasured natural capital input.
Table 7 and Chart 3 present the growth accounts for the mining subsector. MFP growth without natural capital declined in the period from 2000 to 2013 compared with the period from 1980 to 2000. MFP growth slowed from an increase of 1.6% per year to a decline of 4.1% per year from one period to the next, which represents a 5.7-percentage-point slowdown over the two periods. When natural capital input is included, the slowdown in MFP growth is 4.3 percentage points in the two periods from an increase of 1.6% per year to a decline of 2.7% per year. The decline in MFP growth in the mining subsector is found to be partly due to unmeasured natural capital.
| 1980 to 2000 | 2000 to 2013 | |
|---|---|---|
| percent | ||
| Real gross output | 1.0 | 1.1 |
| Contributions | ||
| Labour input | -0.3 | 0.4 |
| Capital input | -0.2 | 2.1 |
| Natural capital input | 0.0 | 0.1 |
| Intermediate input | 0.0 | 1.2 |
| MFP growth | 1.6 | -2.7 |
| Addendum | ||
| Real output growth | 1.0 | 1.1 |
| Labour input growth | -1.2 | 2.9 |
| Capital input growth | -0.5 | 6.6 |
| Natural capital input growth | 1.1 | 0.9 |
| Intermediate input growth | -0.1 | 3.6 |
| MFP growth without natural capital | 1.6 | -4.1 |
| Note: MFP: multifactor productivity. Source: Statistics Canada, author’s calculation based on data from Table 36-10-0217-01. |
||
While incorporating natural capital input improves the measure of capital input and reduces the decline in MFP in the oil and gas extraction and mining subsectors, there is still a long-term decline in MFP. A better understanding of this decline in MFP growth requires microdata on the production activities of mines and estimates of productivity growth for various resource extraction activities such as conventional and non-convention oil extraction. Such data will decompose the decline in MFP growth into the contribution from productivity growth in different types of mines and in different types of resource extraction activities, and the contribution from changes in the composition of these various mines and resource extraction activities.
3.3 Infrastructure capital and multifactor productivity growth in the business sector
Public infrastructure capital (the nation’s roads, bridges, sewer systems and water treatment systems) constitutes a vital input for business-sector production. It contributes to productivity in the private business sector as it enables a concentration of economic resources, provides wider and deeper markets for output and employment, and reduces transportation and production costs.
The contribution of public infrastructure capital to productivity growth can be examined using an extended growth accounting framework (Mas 2006; Gu and Macdonald 2009). The growth accounting framework employed by statistical agencies focuses on private-sector inputs and outputs. The impact of public capital at present is subsumed in MFP.
To explicitly analyze the influence of public capital, changes in MFP from traditional growth accounting for the business sector are decomposed into the contribution from public capital and MFP net of the effect of public capital. This approach adopts the usual assumptions about constant returns to scale across private inputs and private inputs being paid their marginal revenue product. Public capital is assumed to affect output growth, but not the substitution between private capital and labour inputs.
Estimates of MFP net of the contribution of public capital to output growth are calculated as
where denotes MFP in the business sector from growth accounts that focus on private inputs, denotes MFP growth net of the contribution of public capital, and denotes public capital stock in constant dollars. is the elasticity of public capital with respect to the output of the business sector. It indicates the percentage change in business-sector output for a given percentage change in public capital stock. The term in the equation measures the effect of public capital on business-sector output and productivity growth.
The output elasticity can be written as , where denotes value added in constant dollars, and is the marginal product of public capital. If there is a competitive market for the provision of public capital, the value of marginal product of public capital is equal to the user cost of public capital, and the output elasticity of public capital is equal to the share of the cost of public capital in the value of the business-sector output:
Where is the user cost of public capital, is the nominal rate of return, is the depreciation of public capital and is capital gains for public capital or percentage changes in the investment price for public capital. is the investment price for public capital, while is the price of the business-sector output.
In general, the rate of return in the equation can be interpreted as the return to investment in public capital. A large number of studies have estimated the output elasticity and the implied rate of return to public capital. Gu and Macdonald (2009) reported an estimate of the elasticity of output with respect to public infrastructure capital of around 0.1 for the Canadian business sector. The implied rate of return from the elasticity is similar to the nominal after-tax return to capital in the business sector.
Gu and Macdonald (2009) examined the contribution of public infrastructure capital to productivity growth in the business sector for the period from 1961 to 2006. Their results are extended to more recent years in Table 8. The stock of public capital includes the public capital stock of governments and the public health and education sectors. It consists of roads, bridges, sewer systems, water treatment systems, schools and hospitals. The output elasticity of public capital in Equations (10) and (11) is estimated assuming that the rate of return to public capital is equal to the after-tax return on capital in the business sector.
| 1980 to 2000 | 2000 to 2015 | |
|---|---|---|
| percent | ||
| MFP growth | 0.4 | -0.2 |
| Public capital contribution | 0.1 | 0.2 |
| MFP growth net of public capital | 0.4 | -0.4 |
| Note: MFP: multifactor productivity. Source: Statistics Canada, author’s calculation based on data from Table 36-10-0208-01. |
||
Chart 4 presents the growth of public capital stock and business-sector capital stock for the period from 1980 to 2015. During the 1980s and 1990s, the growth in public capital was slower than the growth in capital stock in the business sector as a period of cross-country highway expansion in the 1960s came to an end. In the 2000s, the growth in public capital exceeded the growth in business-sector capital, as a result of large investments in infrastructure from the government’s economic stimulus program during this period.

Data table for Chart 4
| Public capital | Business capital | |
|---|---|---|
| percent | ||
| 1980 | 0.731 | 5.350 |
| 1981 | 1.254 | 5.460 |
| 1982 | 1.368 | 3.013 |
| 1983 | 0.848 | 1.865 |
| 1984 | 0.797 | 1.884 |
| 1985 | 1.409 | 2.484 |
| 1986 | 1.097 | 2.376 |
| 1987 | 1.137 | 3.068 |
| 1988 | 1.382 | 4.050 |
| 1989 | 1.652 | 3.979 |
| 1990 | 2.034 | 3.006 |
| 1991 | 1.885 | 2.191 |
| 1992 | 1.495 | 1.181 |
| 1993 | 1.356 | 0.922 |
| 1994 | 1.741 | 1.749 |
| 1995 | 1.533 | 1.563 |
| 1996 | 1.151 | 1.840 |
| 1997 | 0.261 | 3.283 |
| 1998 | 0.196 | 3.320 |
| 1999 | 1.011 | 3.104 |
| 2000 | 0.979 | 3.011 |
| 2001 | 2.001 | 2.486 |
| 2002 | 2.422 | 1.676 |
| 2003 | 2.016 | 2.294 |
| 2004 | 2.459 | 3.078 |
| 2005 | 3.008 | 3.890 |
| 2006 | 2.956 | 4.206 |
| 2007 | 3.665 | 3.608 |
| 2008 | 3.444 | 3.341 |
| 2009 | 4.844 | 0.537 |
| 2010 | 6.272 | 1.885 |
| 2011 | 3.984 | 2.863 |
| 2012 | 3.182 | 3.356 |
| 2013 | 2.346 | 3.419 |
| 2014 | 1.731 | 3.274 |
| 2015 | 2.063 | 1.858 |
| Source: Statistics Canada, author's tabulation from the underlying data for Table 36-10-0208-01. | ||
Table 8 presents the contribution of public capital to the business sector. Over the period from 1980 to 2000, public capital contributed up to 0.1 percentage points to average MFP growth in the business sector. After 2000, the contribution of public capital to the business-sector MFP growth picked up as a result of increased investment in public infrastructure during this period. It contributed 0.2 percentage points to MFP growth in the business sector for the period from 2000 to 2015.
MFP growth declined in the business sector in the period from 2000 to 2015, compared with the period from 1980 to 2000. This decline in MFP growth is not due to the declining effect of public capital. In fact, the effect on public capital increased after 2000 as a result of increased investment in public capital in this period.
4 Capacity utilization and multifactor productivity growth in manufacturing
Productivity statistics published by Statistics Canada and most other statistical agencies do not correct for short-run variations in capacity utilization. As a result, the changes in MFP growth will reflect the changes in capacity utilization in the short run. In this section, MFP growth is adjusted for short-term changes in capital utilization so that MFP growth better measures technological progress.
Correcting for the effect of variations in capacity utilization is important when rates of capacity utilization change. Canada has recently experienced a resource boom and an appreciation of the Canada United States exchange rate. Based on microdata on plant adjustments to pressures arising from changes in export markets and resulting declines in capacity utilization, Baldwin, Gu and Yan (2013) showed that that the decline in the standard measure of MFP during the early part of the 2000s was partly due to the decline in capacity utilization.
Numerous studies have tried to adjust the MFP measure for capacity utilization. But as Berndt and Fuss (1986) noted, the adjustment is mostly ad hoc, because it lacks a theoretical framework. Gu and Wang (2013) developed a non-parametric procedure for such an adjustment. The adjustment procedure is based on the economic theory of production. Capacity utilization is measured based on the comparison of the ex-post return with the ex-ante expected return on capital. This is intuitively appealing, because changes in the ex-post return on capital should mainly reflect the variation in capacity utilization. A higher level of unused capital and the resulting lower level of capacity utilization should be associated with a lower ex-post rate of return, which is calculated on the actual level of capital. Similarly, a higher level of capacity utilization should be associated with a higher ex-post rate of return on the actual level of capital.
More specifically, the ratio of the user cost of capital based on the ex-post return on capital to the user cost of capital based on the ex-ante return is used to measure capacity utilization. MFP growth is adjusted for changes in capacity utilization using the following equation:
Where is the utilization-adjusted MFP growth based on value added, and is the share of capital costs in the sum of capital and labour costs.
In Equation (12), the ratio of ex-post to ex-ante user cost of capital should be used to adjust the quantity of capital input rather than the price of capital input. This is in contrast to Berndt and Fuss (1986), who argued that the ex-post user cost of capital should be used to value the price of capital input to take into account changes in capacity utilization in measuring MFP. However, as Basu and Fernald (2001) and Hulten (2009) have observed, the Berndt and Fuss procedure does not provide a solution for the issue of capacity utilization in the measurement of MFP.
The measure of capacity utilization used to adjust MFP growth for changes in capacity utilization is constructed as the ratio of the ex-post user cost of capital to the ex-ante user cost of capital. The ex-post user cost of capital is estimated using the five-year moving average of the real internal rate of return.Note This measure of capacity utilization declined from 2000 to 2009, accompanied by a decline in output and employment, and then increased after 2009, accompanied by an increase in output and employment. This trend is consistent with the trend in the industrial capacity utilization rate, which is obtained from the Capital and Repair Expenditures Survey (CAPEX). This rate measures the intensity with which industries use their production capacity and represents the percentage of actual output to potential output.
Table 9 presents MFP growth in manufacturing. Changes in capacity utilization have little effect on MFP growth over the long run. But the changes in capacity utilization have a significant effect on MFP growth in the short run. For example, over the period from 2000 to 2009, MFP without utilization adjustment declined by 0.9% per year. In contrast, MFP adjusted for capacity utilization increased by 0.3% per year over the same period.
| 1980 to 2000 | 2000 to 2009 | 2009 to 2015 | |
|---|---|---|---|
| percent | |||
| MFP growth | 2.1 | -0.9 | 2.2 |
| MFP growth adjusted for capacity utilization | 2.2 | 0.3 | 1.4 |
| Note: MFP: multifactor productivity. Source: Statistics Canada, author’s calculation based on data from Table 36-10-0208-01. |
|||
MFP growth declined in the period from 2000 to 2009 compared with the period from 1980 to 2000. Specifically, it declined from an increase of 2.1% per year to a decline of 0.9% per year a slowdown of 3.0 percentage points in MFP growth over the two periods. When changes in capacity utilization are taken into account, the decline is smaller, from an increase of 2.2% per year to an increase of 0.3% per year in the two periods. This decline in MFP growth is found to be partly due to the decline in the utilization of capital from 2000 to 2009 in manufacturing.
After 2009, output and employment showed positive growth, and capacity utilization increased. MFP increased by 2.2% per year for the period from 2009 to 2015. The positive MFP growth was largely due to an increase in capacity utilization. MFP adjusted for capacity utilization increased by 0.4% per year.Note
5 Do measurement issues matter in slower labour productivity growth after 2000?
Table 10 presents the effect on MFP growth in the business sector when public capital, natural capital and changes in capacity utilization are incorporated. MFP growth slowed in the business sector in the period from 2000 to 2015, compared with the period from 1980 to 2000. It declined by 0.61 percentage points in the two periods, from an increase of 0.43% per year to a decline of 0.18% per year.
| 1980 to 2000 | 2000 to 2015 | 2000 to 2015 less 1980 to 2000 |
|
|---|---|---|---|
| percent | |||
| MFP growth | 0.43 | -0.18 | -0.61 |
| Changes to MFP growth from including the effects of | |||
| Intangible capital | 0.13 | -0.01 | -0.14 |
| Natural capital | 0.04 | 0.13 | 0.09 |
| Public capital | -0.08 | -0.23 | -0.15 |
| Changes in capacity utilization | 0.02 | 0.09 | 0.07 |
| Adjusted MFP growth | 0.54 | -0.20 | -0.75 |
| Note: MFP: multifactor productivity. The overall adjustment is the sum of the adjustments for public capital, natural capital and capacity utilization. Source: Statistics Canada, author’s calculation based on data from Tables 36-10-0208-01 and 36-10-0217-01. |
|||
When natural capital and changes in capital utilization are taken into account, MFP growth slowed by 0.45 percentage points in the two periods, from 0.49% per year to 0.04% per year. About 0.16 percentage points, or 25%, of the decline in MFP growth in the Canadian business sector in the period from 2000 to 2015, compared with the period from 1980 to 2000, is due to an increase in the use of produced capital and in the intermediate inputs required to extract natural resources, with declining ore grades and declining capital utilization in manufacturing.
The decline in labour productivity and MFP growth is not due to changes in intangible and infrastructure capital after 2000. Infrastructure capital contributed to an acceleration of labour productivity and MFP growth after 2000 as a result of a large increase in infrastructure investment in this period. The decline in MFP growth was larger after 2000 when an adjustment was made for the effect of infrastructure and intangible capital.
6 Conclusions
Labour productivity and multifactor productivity (MFP) growth declined in the Canadian business sector after 2000. This paper focuses on the role of measurement issues in the slower productivity growth observed in Canada. First, it extends the asset coverage in the capital input measure to include natural capital, intangible capital and public infrastructure capital so as to examine the role of these capital assets in explaining the recent trend in productivity growth. Second, it takes into account the changes in capital utilization so as to examine the role of these changes in accounting for slower productivity growth in the Canadian manufacturing and business sectors.
The paper finds that only 25% of the decline in MFP growth in the Canadian business sector in the period from 2000 to 2015, compared with the period from 1980 to 2000, is due to an increase in the use of produced capital and in the intermediate inputs required to extract natural resources with declining ore grades, and declining capital utilization in manufacturing. The decline in labour productivity and MFP growth is not due to changes in intangible and infrastructure capital after 2000. Infrastructure capital contributed to an acceleration of labour productivity and MFP growth after 2000 as a result of a large increase in infrastructure investment in this period. The decline in MFP growth was larger after 2000 when an adjustment was made for the effect of infrastructure and intangible capital.
Labour productivity and MFP growth slowed in almost all advanced economies (OECD 2016). Byrne, Fernald and Reinsdorf (2016) examined the role of measurement issues in the slower productivity growth in the United States. Baily and Montalbano (2016) reviewed the research on measurement issues in connection with the U.S. productivity growth slowdown. The results for Canada and the United States suggest that measurement issues alone cannot explain the slowdown in productivity in advanced economies in recent decades. Future research should focus on the role of other factors in the recent productivity growth slowdown in advanced economies factors such as innovation, dissemination of innovation, lack of competition, and decline in business dynamism.
References
ABS (Australian Bureau of Statistics). 2014. 5204.0.55.010 – Information paper: Introduction of Mining Natural Resources into Australia Productivity Measures, 2012-13. Last updated January 27, 2016. Available at: http://www.abs.gov.au/ausstats/abs@.nsf/Latestproducts/5204.0.55.010Main%20Features12012-13?opendocument&tabname=Summary&prodno=5204.0.55.010&issue=2012-13&num=&view= (accessed February 8, 2018).
Adams, P., and W. Wang. 2015. Accounting for Natural Capital in Productivity in the Mining and Oil and Gas Sector. Analytical Studies Branch Research Paper Series, no. 372. Statistics Canada Catalogue no. 11F0019M. Ottawa: Statistics Canada.
Ahmad, N., and P. Schreyer. 2016. “Are GDP and productivity measures up to the challenges of the digital economy?” International Productivity Monitor 30: 4 – 27.
Almon, M.J., and J. Tang. 2011. “Industrial structural change and the post-2000 output and productivity growth slowdown: A Canada-U.S. comparison.” International Productivity Monitor 22: 44 – 81.
Baily, M.N., and N. Montalbano. 2016. Why is U.S. Productivity Growth So Slow? Possible Explanations and Policy Responses. Working paper presented at a joint IBPP-Huchins Center conference on the productivity slowdown held at the Brookings Institution, Washington, D.C., on September 9, 2016. Available at: https://www.brookings.edu/research/why-is-us-productivity-growth-so-slow-possible-explanations-and-policy-responses/ (accessed February 8, 2018).
Baldwin, J.R., W. Gu, A. Lafrance, and R. Macdonald. 2009. Investment in Intangible Assets in Canada: R&D, Innovation, Brand, and Mining, Oil and Gas Exploration Expenditures. The Canadian Productivity Review, no. 26. Statistics Canada Catalogue no. 15-206-X. Ottawa: Statistics Canada.
Baldwin, J.R., W. Gu, and R. Macdonald. 2012. Intangible Capital and Productivity Growth in Canada. The Canadian Productivity Review, no. 29. Statistics Canada Catalogue no. 15-206-X. Ottawa: Statistics Canada.
Baldwin, J.R., W. Gu, R. Macdonald, W. Wang, and B. Yan. 2014. Revisions to the Multifactor Productivity Accounts. The Canadian Productivity Review, no. 35. Statistics Canada Catalogue no. 15-206-X. Ottawa: Statistics Canada.
Baldwin, J.R., W. Gu, and B. Yan. 2013 “Export growth, capacity utilization and productivity growth: Evidence for Canadian manufacturing plants.” Review of Income and Wealth 59: 665 – 688.
Baldwin, J.R., and M. Willox. 2016. The Industry Origins of Canada’s Weaker Labour Productivity Performance and the Role of Structural Adjustment in the 1990s and the 2000s. Analytical Studies Branch Research Paper Series, no. 373. Statistics Canada Catalogue no. 11F0019M. Ottawa: Statistics Canada.
Balk, B.M. 2010. “An assumption-free framework for measuring productivity change.” The Review of Income and Wealth 56 (1): S224 –S256.
Balk, B.M. 2015. “Measuring and relating aggregate and subaggregate total factor productivity change without neoclassical assumptions.” Statistica Neerlandica 69 (1): 21 – 48.
Basu, S., and J. Fernald. 2001. “Why is productivity procylical? Why do we care?” In New Directions in Productivity Analysis, Studies in Income and Wealth, ed. E. Dean, M.J. Harper, and C. Hulten, Vol. 63. Chicago: University of Chicago Press.
Basu, S., and J. Fernald. 2002. “Aggregate productivity and aggregate technology.” European Economic Review 56 (6): 963 991.
Berndt, E.R., and M.A. Fuss. 1986. “Productivity measurement with adjustments for variations in capacity utilization and other forms of temporary equilibrium.” Journal of Econometrics 33: 7 29.
Bruno, M. 1978. “Duality, intermediate inputs and value added.” In Production Economics: A Dual Approach to Theory and Applications, ed. M. Fuss and D. McFadden, vol. 2. Amsterdam: North-Holland.
Brynjolfsson, E., and J.H. Oh. 2012. The Attention Economy: Measuring the Value of Free Digital Services on the Internet. Working Paper. International Conference on Information Systems 4: 3243 3261.
Byrne, D.M., J.G. Fernald, and M.B. Reinsdorf. 2016. Does the United States Have a Productivity Slowdown or a Measurement Problem? Brookings Paper on Economic Activity. Washington, D.C.: The Brookings Institution.
Cette, G., J.G. Fernald, and B. Mojon. 2016. The Pre-Great Recession Slowdown in Productivity. Federal Reserve Bank of San Francisco Working Paper 2016‑08. Available at: http://www.frbsf.org/economic-research/publications/working-papers/wp2016-08.pdf (accessed February 9, 2018).
Corrado, C., C. Hulten, and D. Sichel. 2009. “Intangible capital and U.S. economic growth.” Review of Income and Wealth 55 (3): 661 685.
Diewert, W.E. 1976. “Exact and superlative index numbers.” Journal of Econometrics 4: 115 145.
Diewert, W.E. 2014. A Note on Reconciling Gross Output TFP Growth with Value Added TFP Growth. Discussion Paper 14-12. Vancouver, B.C.: School of Economics, University of British Columbia. Available at: https://www.economics.ubc.ca/files/2014/12/pdf_paper_erwin-diewert-14-12-Reconciling.pdf (accessed February 9, 2018).
Diewert, W.E., and E. Yu. 2012. “New estimates of real income and multifactor productivity growth for the Canadian business sector, 1961-2011.” International Productivity Monitor 24: 27 48.
Domar, E. 1961. “On the measurement of technical change.” Economic Journal 71: 710 729.
Durand, René. 1996. “Canadian input-output-based multi-factor productivity accounts.” Economic Systems Research 8 (4): 367 390.
Gu, W., and R. Macdonald. 2009. The Impact of Public Infrastructure on Canadian Multifactor Productivity Estimates. The Canadian Productivity Review, no. 21. Statistics Canada Catalogue no. 15-206-X. Ottawa: Statistics Canada.
Gu, W., and W. Wang. 2013. “Correction for variations in capacity utilization in the measurement of productivity growth: A non-parametric approach.” Journal of Economic and Social Measurement 38 (4): 347 369.
Hall, R. 1990. “Invariance properties of Solow’s productivity residual.” In Growth, Productivity, Employment, ed. P. Diamond. Cambridge, Massachusetts: MIT Press.
Harper, M.J., A.O. Nakamura, and L. Zhang. 2012. “Difficulties assessing multifactor productivity growth in Canada.” International Productivity Monitor 24: 76 – 84.
Hulten, C.R. 2009. Growth Accounting. NBER Working Paper no. 15341. Cambridge, Massachusetts: National Bureau of Economic Research.
Hulten, C.R., and P. Schreyer. 2010. GDP, Technical Change, and the Measurement of Net Income: The Weitzman Model Revisited. NBER Working Paper no. 16010. Cambridge, Massachusetts: National Bureau of Economic Research.
Jorgenson, D.W. 1966. “The embodiment hypothesis.” Journal of Political Economy 74 (1): 1 17.
Jorgenson, D.W. 2012. “The World KLEMS Initiative.” International Productivity Monitor 24: 5 19.
Jorgenson, D.W., F.M. Gollop, and B. Fraumeni. 1987. Productivity and U.S. Economic Growth. Cambridge, Massachusetts: Harvard University Press.
Jorgenson, D.W., M.S. Ho, and K. Stiroh. 2005. Information Technology and the American Growth Resurgence. Cambridge, Massachusetts: MIT Press.
Mas, M. 2006. Infrastructures and New Technologies as Sources of Spanish Economic Growth. MPRA Paper no. 15795. Munich, Germany: University of Munich.
Nakamura, L., J. Samuels, and R. Soloveichik. 2016. Valuing “Free” Media in GDP: An Experimental Approach. Washington, D.C.: U.S. Department of Commerce, Bureau of Economic Analysis.
OECD (Organisation for Economic Co-operation and Development). 2015. The Future of Productivity. Paris: OECD.
OECD (Organisation for Economic Co-operation and Development). 2016. OECD Compendium of Productivity Indicators, 2016. Paris: OECD.
Olewiler, N. “Canada’s dependence on natural capital wealth: Was Innis wrong?” Annual Conference of the Canadian Economics Association, Antigonish, Nova Scotia. June 1 to 4, 2017. Innis Lecture.
Rao, S., A. Sharpe, and J. Smith. 2005. “An analysis of the labour productivity growth slowdown in Canada since 2000.” International Productivity Monitor 10: 3 – 23.
Schreyer, P. 2001. Measuring Productivity: OECD Manual. Paris: Organisation for Economic Co-operation and Development.
Schreyer, P. 2010. “Measuring multi-factor productivity when rates of return are exogenous.” In Price and Productivity Measurement: Volume 6, Index Number Theory, ed. W.E. Diewert, B.M. Balk, D. Fixler, K.J. Fox and A.O. Nakamura, chapter 2, p. 13 40. Bloomington, Indiana: Trafford Press.
Schreyer, P. 2012. Productivity Measurement and Natural Assets: An Extended Growth Accounting Approach. Paris: Organization for Economic Co-operation and Development. Draft.
Sharpe, A., and A. Murray. Explanations for the U.S. Productivity Growth Slowdown. Paper presented at the annual conference of the Canadian Economics Association, Antigonish, Nova Scotia, June 2, 2017.
Timmer, M.P., R. Inklaar, M. O’Mahony, and B. van Ark. 2011. “Economic growth in Europe: A comparative industry perspective.” International Productivity Monitor 21: 3 23.
Topps, V., and T. Kuluys. 2014. “On productivity: The influence of natural resource inputs.” International Productivity Monitor 27: 64 78.
Varian, H. Economic value of Google to US Advertisers and Customers. Keynote address at the Web 2.0 Expo 2011 Conference, San Francisco, March 28 31, 2011.
Veldhuizen, E., and M. de Haan. The Dutch growth accounts: Measuring productivity with non-zero profits. Paper prepared for the 32nd General Conference of the International Association for Research in Income and Wealth, Boston, Massachusetts, August 5 11, 2012.
- Date modified:
