Analytical Studies Branch Research Paper Series
Going the Distance: Estimating the Effect of Provincial Borders on Trade when Geography Matters
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
by Robby K. Bemrose, W. Mark Brown and Jesse Tweedle
Economic Analysis Division
Statistics Canada
Acknowledgements
The authors would like to thank Danny Leung, Bart Los, Dennis Novy, Trevor Tombe, Dan Trefler, Yoto Yotov and participants at the Economic Analysis Division and Université du Québec à Montréal seminar series and at the North American Regional Science Council and Western Regional Science Association meetings for their helpful comments. The authors are grateful for research assistance from Javad Sadeghzadeh, Olena Melin, and Afshan Dar-Brodeur.
Abstract
For many goods, such as dairy products and alcoholic beverages, the presence of substantial (non-tariff) barriers to provincial trade is widely recognized. If these non-tariff barriers matter, intraprovincial trade should be stronger than interprovincial trade, all else being equal. However, comparing intraprovincial and interprovincial trade levels is challenging, because intraprovincial trade is heavily skewed toward short-distance flows. When these are not properly taken into account by gravity-based trade models, intraprovincial trade levels—provincial border effects—tend to be overestimated. To resolve this problem, new sub-provincial trade flows developed from a set of transaction-level transportation files are used to estimate provincial border effects. The sensitivity of the results to distance is captured by estimating models across standard geographies of varying size (provinces, economic regions, census divisions) and non-standard geographies (hexagonal lattices) of differing size and placement via a series of simulations. The results show that provincial border effects diminish as distance is measured more accurately and geographies are more fine-grained and uniform in shape and size. Nonetheless, border effects persist, with an implied ad valorem tariff equivalent of 6.9%. This contrasts with the United States, where state border effects are eliminated when similar approaches are applied.
Key words: Border effects, interprovincial trade, transportation costs, gravity model
JEL: R4 R15 F15
Executive summary
For many goods, such as dairy products and alcoholic beverages, the presence of substantial (non-tariff) barriers to provincial trade is widely recognized. If these non-tariff barriers matter, intraprovincial trade should be stronger than interprovincial trade, all else being equal. However, comparing intraprovincial and interprovincial trade levels is challenging, because intraprovincial trade is heavily skewed toward short-distance flows. When these are not properly taken into account, intraprovincial trade levels—provincial border effects—tend to be overestimated.
To resolve this problem, sub-provincial trade flows developed from a set of transaction-level transportation files are used to estimate provincial border effects during the 2004-to-2012 period. Each shipment is measured in terms of value, cost, distance shipped, and origin and destination. Based on the origin and destination points (latitudes and longitudes), flows between regions of any size can be used, which makes possible the estimation of flows between regions within and across provincial borders.
The analysis shows that intraprovincial trade is consistently stronger than interprovincial trade when the distance between the trading regions and the ability of the trading units to generate and absorb trade flows are taken into account. The relative strength of intraprovincial trade depends on the geographic units used to measure trade. When provinces are used, within-province trade is estimated to be 2.26-fold greater than interprovincial trade. This suggests that the impediments to interprovincial trade are equivalent to imposition of a 13.6% ad valorem tariff. When sub-provincial areas are used instead of provinces, the border-effect tariff equivalent falls to 6.9%. This lower estimate proved to be robust to a large number of statistical tests. It also contrasts with the United States, where state border effects are eliminated when similar approaches are applied.
1. Introduction
For some goods, such as dairy products and alcoholic beverages, substantial (non-tariff) barriers to interprovincial trade exist. However, the degree to which these barriers are reflected in the level of interprovincial trade is not clear. One way to assess this is to determine if provinces trade more with themselves than with each other. If non-tariff barriers matter, their imprint should be seen in patterns of provincial trade.
Efforts to investigate if this is the case have been hampered by a lack of data that allow the estimation of trade flows within provinces, as it is against these flows that trade between provinces is compared. The problem is overcome by developing estimates of intraprovincial and interprovincial trade from a set of transaction-level flows. Using a gravity-based trade model, this study compares trade among regions within provinces with trade between provinces, thereby providing an estimate of the extent to which provincial economies are integrated through trade—that is, the degree to which provincial borders dampen provincial trade, what is commonly called the “border effect.”
Building on McCallum’s (1995) initial work, a large literature has been devoted to measuring border effects, national and subnational. Over time, estimated border effects have been reduced as McCallum’s initial specification was modified to take into account the effects of market access and competition (Anderson and van Wincoop 2003; Anderson and Yotov 2010); estimates of distance were refined (Head and Mayer 2010); and new estimators were applied (Head and Mayer 2014). Still, a consistent finding has been that trade is stronger within countries than between them.
While much of the literature focused on measuring border effects between countries, the same methods have been applied to subnational regions. The arc of the intra-national border effects literature has also been a reduction of effects with the application of more refined methods. In some instances, this led to elimination of the border effect altogether. In the United States, initially high estimates of interstate border effects (Wolf 2000) were reduced by more accurate measures of distance (Hillberry and Hummels 2003, Head and Mayer 2010, and Crafts and Klein 2015), restricting trade flows to shipments from manufacturers (Hillberry and Hummels 2003), using a panel specification and controlling for internal migration (Millimet and Osang 2007), and more fine-grained geographies to define subnational trading units (Hillberry and Hummels 2008; see also Coughlin and Novy 2016).
Two strategies might be used to develop an estimate of provincial border effects. One is to further refine the now-standard estimators in order to mitigate measurement error and missing variable bias. This is the approach of Agnosteva, Anderson and Yotov (2014), who take advantage of the panel nature of current measures of intraprovincial and interprovincial trade to estimate provincial border effects. The second, and arguably complementary strategy, which is employed in this study, is to further develop data on intraprovincial and interprovincial trade in order to address concerns raised in the literature, while also using an estimation strategy that seeks to reduce remaining biases.
Particular attention is paid to the influence of measured distance (Head and Mayer 2010) and geography (Hillberry and Hummels 2003, 2008). Head and Mayer (2010) show that inaccurate measures of distance can bias estimates of the border effect upward, because intraregional distances tend to be overestimated relative to interregional distances. By estimating distance based on actual point-to-point flows of goods, this bias is effectively eliminated. Hillberry and Hummels (2008) demonstrate that as the size of the geographic unit of analysis is reduced, estimated barriers to state trade fall to zero. Interstate barriers are an artefact of the geographic scale at which estimates are made. This effect stems from the larger number of short-distance flows of intermediate goods covered by the U.S. Commodity Flow Survey (CFS), which results in inaccurate estimates of the distance travelled by goods. An impediment to this work, particularly in the Canadian context, is the lack of detailed sub-provincial data that would take the biasing effect of short-distance flows into account. The problem is addressed by taking advantage of the micro-data used to calculate intraprovincial and interprovincial trade flows.
The analysis shows that intraprovincial trade is consistently stronger than interprovincial trade after the distance between the trading regions and the ability of the trading units to generate and absorb trade flows are taken into account. The relative strength of intraprovincial trade depends on the geographic units used to measure it, and to a lesser degree, the distance measure employed. When sub-provincial areas are used instead of provinces, the border effect tariff equivalent falls from 13.6% to 6.9%. The latter is the estimate that held after application of an extensive set of checks aimed at mitigating the upward biasing effects of model misspecification (non-linear effects of distance) and geography (size and placement of the geographic units). It is, therefore, a conservative, low-end estimate that contrasts sharply with the United States, where the application of similar approaches eliminates state border effects.
The remainder of this paper is organized as follows. Section 2 (Data development) reviews the method used to estimate trade between sub-provincial geographic units and builds a picture of internal Canadian trade. Particular attention is paid to how these estimates are benchmarked to known intraprovincial and interprovincial trade totals and to the underlying validity of these estimates. Section 3 (Model and estimation strategy) outlines the structure of the trade model and the identification of an appropriate estimator. Section 4 (Model estimates) presents the estimates, building from standard intraprovincial and interprovincial estimates through trade based on sub-provincial geographic units to a set of robustness checks that test for biases associated with misspecification and the Modifiable Areal Unit Problem (MAUP). Section 5 (Border effect tariff equivalent) estimates tariff-equivalent barriers to interprovincial trade in aggregate and by commodity. Section 6 (Conclusions) concludes with a summary of the results and their implications.
2. Data development
Up to now, analysis of Canada’s internal trade has been limited to the provincial level, relying on trade tables from the provincial input-output accounts or from provincial trade patterns reported by the Annual Survey of Manufactures (see Brown [2003] for the latter). This report develops a new flexible transaction-level point-to-point dataset that permits measurement of trade flows between an almost limitless set of sub-provincial geographic units, thereby providing a means to address many of the econometric issues raised in the literature. Because this database is new, it is useful to outline how it was constructed and describe some of its basic characteristics.
2.1 Database construction
The data are from Statistics Canada’s Surface Transportation File (STF), which provides estimates of the value of goods traded between regions in Canada, and between Canada and the United States. The STF is derived from the Trucking Commodity Origin and Destination Survey (TCOD) and railway waybills for the 2002-to-2012 period, with the analysis focusing on the 2004-to-2012 period.Note 1 Because these data are constructed from the trucking and rail waybill data, the STF in its original form is a “logistics file”.Note 2
The STF measures the movement of goods from the point where they are picked up to the point where they are dropped off. These points do not necessarily represent locations where goods are made or where they are used. However, the analysis requires a database that captures the level of trade between sub-provincial regions, which is embedded as a concept in the gravity-based trade model applied here. This objective has much in common with those stipulated when developing the provincial input-output accounts:
“In analyzing economic interdependence, it is necessary to maintain the link between the original supply sources and final consumers, by commodity. It follows then that the point of origin (the original supply source) is where goods and services are produced or goods are sold out of inventory stocks of producers, wholesalers and retailers. The point of destination (i.e., the final consumer) is the point where goods and services are purchased for current consumption, capital formation, input into the production process of other commodities, or added to inventory stocks.” (Généreux and Langen 2002, p. 7)
To transform the STF from a logistics file to a trade file, provincial trade flows from the input-output accounts are used to benchmark intraprovincial and interprovincial flows by commodity. Each transaction in the STF is given a weight such that the aggregate adds to the total for the corresponding intraprovincial or interprovincial flow from the input-output tables. The benchmarking procedure and, in particular, the development of a concordance between the Input-Output Commodity Classification (IOCC) and the Standard Classification of Transported Goods (SCTG) (Statistics Canada, n.d.a) codes on the STF file, is explained in Appendix A.3. A synopsis of the procedure is presented here.
The nominal value of trade between sub-provincial regions (hereafter, regions) and , , is the sum of the survey weighted value of shipment indexed by between origin region and destination region ,Note 3 multiplied by the benchmark weight for shipment :
The shipment benchmark weight is the shipment-based survey weight, , multiplied by the province pair benchmark weight for the commodity being shipped, with notation for the province pair and commodity suppressed to simplify the exposition. The benchmark weight is set such that trade between a given province pair (or within the same province) adds to known totals from the provincial trade accounts by detailed commodity and year.
Figure 1 illustrates the benchmarking procedure. Consider the toy example of flows of vehicles made in various locations in Ontario and ultimately used at various locations in Manitoba and Saskatchewan. The vehicles may first be shipped to a distribution centre in Manitoba, with a portion of the shipment sent to Saskatchewan, which is represented by the unbenchmarked flows in the upper left-hand quadrant of the figure. From a logistics perspective, this is a correct representation of the flows, but from a trade perspective, the flow from Ontario where the vehicles are made to Saskatchewan where they are used is underestimated, and the flow from Manitoba to Saskatchewan is overestimated. As presented in Figure 1 (top right quadrant), benchmarking to the input-output tables weights up the flow from Ontario to Saskatchewan and weights down (to zero) the flow from Manitoba to Saskatchewan.
The weighting strategy relies on there being a flow on the STF between each province pair; otherwise, there is nothing to weight up (or down): . The result is no flow between the province pairs (lower half of Figure 1). If these “broken links” are too common and/or correlated with the distance between the province pairs, benchmarking will result in biased estimates. One source of bias is simply replaced by another.
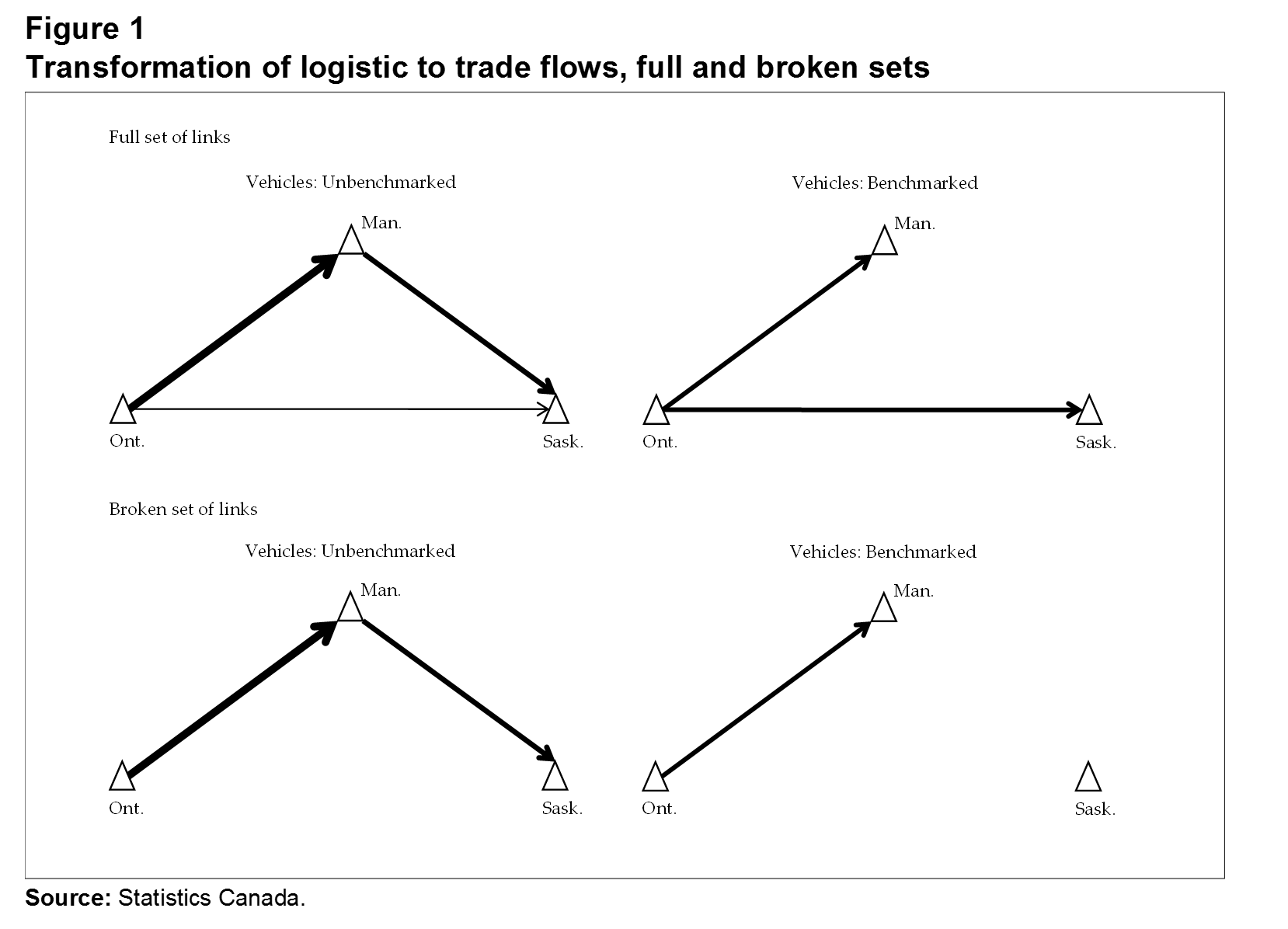
Description for Figure 1
The title of Figure 1 is "Transformation of logistic to trade flows, full and broken sets."
The diagram depicts the benchmarking process, which is represented by four triangles delineated by arrows of different widths. Not all triangles are fully delineated by arrows because the arrows represent the trade flows. On the three points of each of the four triangles are small triangles named Ontario, Manitoba and Saskatchewan. Ontario is the province of origin of the trade flows.
Two of these four triangles represent the full set of links, one for unbenchmarked vehicles and the other for benchmarked vehicles.
In the triangle for unbenchmarked vehicles, the goods are shipped between Ontario, Manitoba, and Saskatchewan.
In the triangle for benchmarked vehicles, the goods are shipped only between Ontario and Manitoba and between Ontario and Saskatchewan.
The other two triangles represent the broken set of links, one for unbenchmarked vehicles and the other for benchmarked vehicles.
In the triangle for unbenchmarked vehicles, the goods are shipped between Ontario and Manitoba and between Manitoba and Saskatchewan.
In the triangle for benchmarked vehicles, the goods are shipped only from Ontario to Manitoba.
The source of this figure is “Statistics Canada.”
Table 1 presents the ratio of the benchmarked STF interprovincial or intraprovincial flows to the actual flows from the input-output tables. Because the Atlantic Provinces had a larger number of broken links, particularly with Western Canada, they were aggregated for benchmarking. As a result, there are relatively few pairs with a serious loss of trade. The overall percentage is 99% of the input-output based trade levels. Intraprovincial flows tend to have less of a loss, but this is small. Otherwise, there do not appear to be large losses with distance. For instance, the loss for Atlantic Canada’s exports to Alberta or British Columbia is about the same as Ontario’s loss. The effect of these broken links is tested further below by estimating the gravity model with the input-output-derived provincial flows and the benchmarked flows; both sets of data provide qualitatively similar results (see Section 4).
| Destination | ||||||||
|---|---|---|---|---|---|---|---|---|
| Atlantic Canada | Que. | Ont. | Man. | Sask. | Alta. | B.C. | Total | |
| percent | ||||||||
| Origin | ||||||||
| Atlantic Canada | 99 | 99 | 89 | 94 | 77 | 94 | 89 | 95 |
| Quebec | 99 | 99 | 100 | 98 | 94 | 98 | 98 | 99 |
| Ontario | 100 | 100 | 100 | 99 | 98 | 100 | 100 | 100 |
| Manitoba | 93 | 97 | 95 | 96 | 95 | 97 | 95 | 96 |
| Saskatchewan | 87 | 96 | 96 | 95 | 98 | 97 | 97 | 97 |
| Alberta | 89 | 97 | 98 | 97 | 99 | 100 | 100 | 99 |
| British Columbia | 96 | 82 | 99 | 97 | 96 | 99 | 98 | 97 |
| Total | 98 | 99 | 99 | 97 | 98 | 99 | 98 | 99 |
| Note: Shares are based on the average level of trade between 2004 and 2012. Source: Statistics Canada, authors' calculations. |
||||||||
While benchmarking accounts for the level of intraprovincial and interprovincial trade, the pattern of trade, especially within provinces, may be affected by the functioning of the transport/distribution system—that is, shorter-distance logistics-driven flows may be more prevalent. This has important implications because, when pooled with interprovincial flows, these shorter-distance, intraprovincial flows tend to be underestimated, biasing the estimated interprovincial border effect upward.
As with the toy example above, the effect of benchmarking should be to stretch out interprovincial trade, as short-distance flows to/from distribution centres or wholesalers are weighted down, and longer-distance flows from points where goods are produced to where they are used are weighted up. This is apparent in Figure 2, which reports the shipment distance kernel densities with survey weights and survey and benchmark weights together , with shipment distances divided between interprovincial and intraprovincial flows. As expected, for interprovincial shipments, benchmarking tends to reduce the importance of shorter-distance flows (less than 1,000 km) and increase the importance of longer-distance flows, particularly those exceeding 3,000 km. For intraprovincial trade, after benchmarking, short-distance flows are reduced, as imported commodities (for instance, shoes and apparel) that are distributed locally are weighted downward. Still, within provinces, short-distance logistics-driven flows may be more prevalent. This effect can be tested by observing whether distance has a stronger effect on intraprovincial trade relative to interprovincial trade. The results indicate that this is not the case (Appendix B.1 contains a detailed discussion).

Description for Figure 2
The title of Figure 2 is "Intra-provincial and interprovincial distance, benchmark and survey weights."
This is a line chart of kernel densities.
The horizontal axis is “Distance (kilometres)”. It starts at 0 and ends at 5,000, with tick marks every 1,000 points.
The vertical axis is “Density”. It starts at 0 and ends at 0.01, with tick marks every 0.002 points.
There are 4 series in this graph.
The title of series 1 is "Intra (survey)," the intra-provincial survey-weighted density of distance. It starts out really high and drops significantly after around 100 kilometres, and is flat thereafter.
The title of series 2 is "Intra (benchmark)," the intra-provincial benchmark-weighted density of distance. It starts out really high and drops significantly after around 100 kilometres, and is flat thereafter. It is lower than series 1 at the start, but then crosses it around 50 kilometres and is higher than series 1 thereafter.
The title of series 3 is "Inter (survey)," the interprovincial survey-weighted density of distance. It starts out low, peaks around 500 kilometres, and is relatively constant thereafter, with bumps around 3,400 kilometres and 4,400 kilometres. It is higher than series 1 and 2.
The title of series 4 is "Inter (benchmark)," the interprovincial benchmark-weighted density of distance. It starts out low, peaks around 50 kilometres, and is relatively constant thereafter, with bumps around 3,400 kilometres and 4,400 kilometres. It is higher than series 1 and 2. It is slightly lower than series 3 before 2,000 kilometres, and slightly higher than series 3 thereafter.
The source of Figure 2 is “Statistics Canada, authors’ calculations.”
For additional information, please contact Statistics Canada at STATCAN.infostats-infostats.STATCAN@canada.ca.
2.2 Patterns of trade
Before estimating interprovincial barriers to trade, it is helpful to provide a picture of trade between provinces and between sub-provincial regions.
Table 2 shows the pattern of exports across provinces (and Atlantic Canada) averaged over the 2004-to-2012 period. With the exceptions of Saskatchewan, Manitoba and Atlantic Canada, most trade occurs within provinces. This is not necessarily because of interprovincial barriers, but because of the influence of distance on trade flows (Figure 2). Table 2 also demonstrates provinces’ tendency to trade with those nearby. Atlantic Canada’s most important export market is Quebec; Saskatchewan’s is Alberta. However, although intraprovincial flows are large, the pattern of trade within provinces is not known.
| Atlantic Canada | Que. | Ont. | Man. | Sask. | Alta. | B.C. | Total | |
|---|---|---|---|---|---|---|---|---|
| percent | ||||||||
| Atlantic Canada | 28 | 34 | 24 | 5 | 1 | 5 | 4 | 100 |
| Quebec | 1 | 67 | 22 | 1 | 1 | 4 | 3 | 100 |
| Ontario | 1 | 11 | 76 | 2 | 1 | 6 | 4 | 100 |
| Manitoba | 1 | 7 | 18 | 48 | 6 | 14 | 6 | 100 |
| Saskatchewan | 0 | 4 | 13 | 8 | 44 | 24 | 6 | 100 |
| Alberta | 0 | 4 | 9 | 4 | 5 | 68 | 10 | 100 |
| British Columbia | 0 | 5 | 8 | 2 | 2 | 15 | 68 | 100 |
| Total | 1 | 23 | 42 | 4 | 4 | 16 | 10 | 100 |
| Note: Shares are based on the average level of trade between regions for the period from 2004 to 2012. Percentages may not add up to 100% because of rounding. Source: Statistics Canada, authors' calculations. |
||||||||
Patterns of intraprovincial and interprovincial trade are determined by a discrete set of origins and destinations. Map 1 displays the locations that are served by truck and/or rail. Each point represents a location that participates in trade, generating a potential surface where goods are most likely to be made and used. On this surface, any given geography—province, economic region (ER), census division (CD) or other configuration—is overlaid to generate a set of aggregate flows.
As is evident in Map 1, while most trade occurs within provinces, the greatest potential for trade is even more geographically concentrated. This is confirmed when total trade (exports plus imports) by value across ERs is calculated as a percentage of overall goods trade in Canada. A small minority of ERs accounts for a disproportionate share of internal trade. Of the 73 ERs, three (Toronto, Montréal and Hamilton–Niagara Peninsula) account for 30% of the value of goods shipped in Canada. More trade moves in and out of the Toronto ER than any province except Ontario and Quebec. Thus, understanding provincial trade means understanding trade between sub-provincial regions, especially large urban centres.
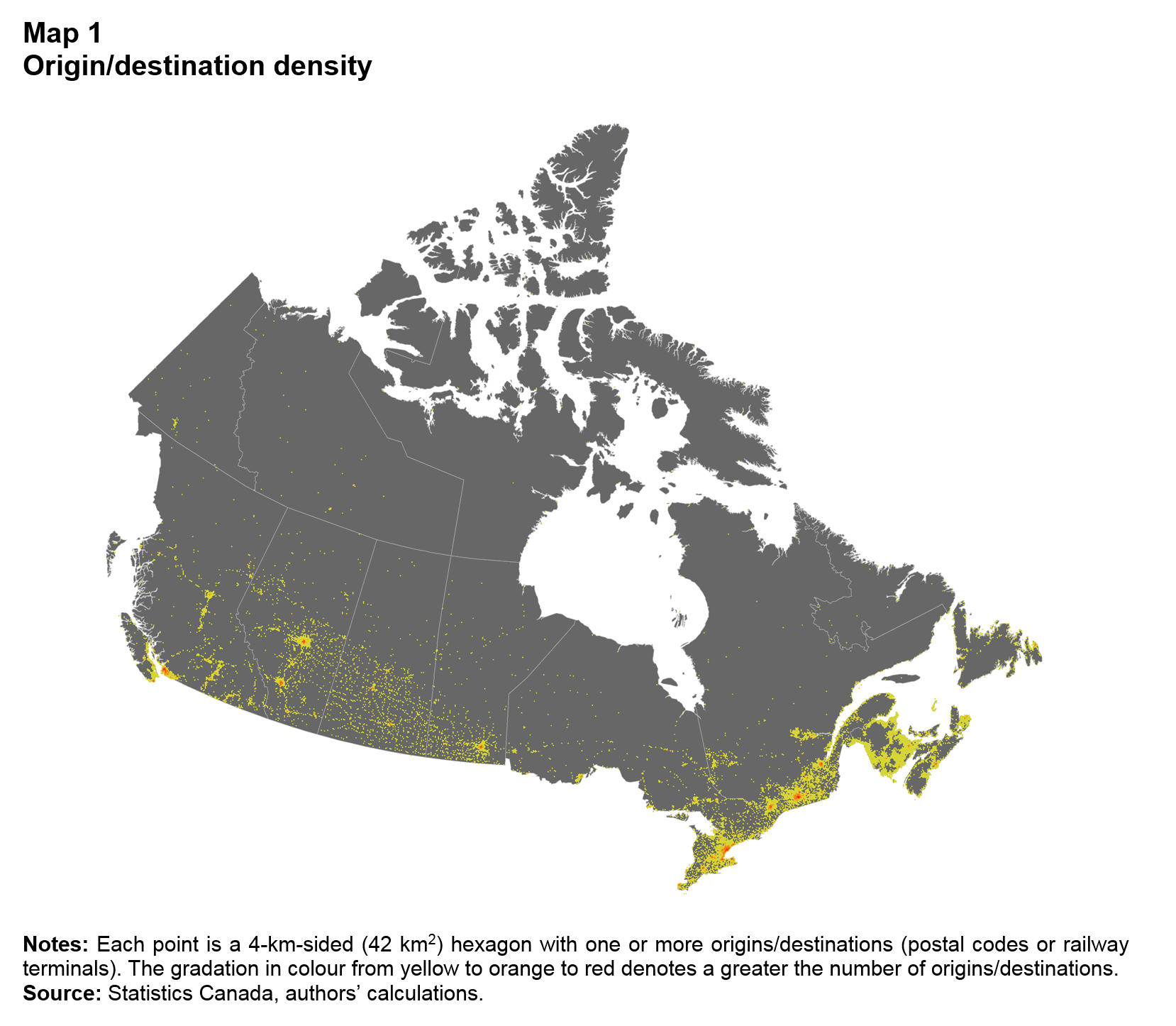
Description for Map 1
The title of Map 1 is "Origin/destination density."
The map depicts Canada and shows provincial and territorial boundaries.
It is a map of the density of locations in the Surface Transportation File (STF).
Places in Canada with a high amount of trade activity are coloured in red.
The places with the most trade activity are concentrated around major cities: Toronto, Ottawa, Montréal, Quebec City, Calgary, Edmonton and Vancouver.
Other places have a medium amount of trade.
There is less activity in rural areas.
The notes for Map 1 are as follows:
Notes: Each point is a 4km-sided (42km2) hexagon with one or more origins/destinations (postal codes or railway terminals). The gradation in colour from yellow to orange to red denotes a greater the number of origins/destinations.
The source of Map 1 is “Statistics Canada, authors’ calculations.”
For additional information, please contact Statistics Canada at STATCAN.infostats-infostats.STATCAN@canada.ca.
3. Model and estimation strategy
Estimation of provincial border effects relies on the development of data of sufficient quality to generate well-founded estimates and a model and estimator that are appropriate for the data.
3.1 Trade model
As is standard in the literature (Head and Mayer 2014),Note 4 trade between regions and is treated as multiplicative function of the capacity of to serve export markets , the absorptive capacity of export market in , and a measure that captures the effect of trade costs between and :
where is a constant term. This general form can be expressed as a structural gravity model:
where is the value of output in and is the sum of exports across all trading partners (including itself) , and is the value of consumption in and is the sum of imports across all trading partners (including itself) . The terms and are multilateral resistance terms (Anderson and van Wincoop 2003), where
is a measure of market access for exporting region , and measures the level of competition in market . Trade costs are accounted for by the distance between and and a set of binary variables that account for intraprovincial and intraregional trade .
3.2 Estimator
Equation (3) can be estimated by substituting fixed effects for and , adding a multiplicative error term and taking the exponent of the right-hand-side:
where and take into account the ’s output and market potential and ’s size and level of competition , respectively.
This estimation strategy has become the standard means of estimating the gravity modelNote 5 (Anderson and Yotov 2012), because of ease of estimation, and because the fixed effects may pick up origin- and destination-specific unobservables that can bias full information-based estimates (Anderson 2010 and Head and Mayer 2014).
Missing-variable bias is particularly important in this work. Although every effort is made to assign trade flows to where goods are made and used, there may be cases where a destination is acting as a distribution centre, thereby inflating its level of export and imports. Also, some provinces (for example, British Columbia) may have stronger ties with world markets than with other provinces, which reduces their role as a domestic trading partner. In both instances, the fixed effects should account for these unobservables, which affect the level of trade in and out of a region (Head and Mayer 2014).
Ordinary least squares (OLS), the standard approach to estimating Equation (5), introduces two potential sources of bias. First, OLS estimates of a log-linearized multiplicative model are biased in the presence of heteroscedastic errors (Santos Silva and Tenreyro 2006). Second, OLS estimates are biased in instances with a larger number of zero flows, which are dropped when the gravity model is estimated using OLS (Head and Mayer 2014). The latter is particularly important here, because the models are estimated using flows between sub-provincial regions, which results in many zero flows between actively trading region pairs.
The first step in addressing these problems is to determine if the error term is heteroscedastic. To do so, the Manning and Mullahy (2001) test is applied. It is estimated based on the following specification:
Where is the predicted log-level of trade from the OLS estimation of (5) and is the difference between the data and the fitted values from the same estimator. Without zero flows, Head and Mayer (2014) find when the data-generating process produces log normal errors, but when the process produces (Poisson) heteroscedastic errors. In Table 3, the estimates of are presented for estimates by province, ER and CD. For provincial trade, the point estimate for is 2.11, suggesting log-normal errors. However, when the model is estimated by ER and CD, the point estimates for are about 1.7. For ERs, where the number of zero flows is around 8%, the estimate is close to what would be expected based on Monte Carlo simulations (Figure 4 in Head and Mayer 2014). For the CD estimates, where almost half the pairs have zero flows, the expected value of is 1.6, with the actual estimate at 1.7. However, this is close to what Head and Mayer find when they obtain estimates of from real data. The upshot is that, in both instances, the estimate for is significantly different from 2, suggesting the OLS estimator is inappropriate.
| Geography | Κ | 95% confidence interval |
Number of observations |
|
|---|---|---|---|---|
| Lower bound | Upper bound | |||
| Province | 2.11 | 1.92 | 2.30 | 100 |
| Economic region | 1.71 | 1.68 | 1.74 | 5,069 |
| Census division | 1.68 | 1.67 | 1.69 | 47,156 |
| Notes: Κ is estimated with Equation (6) using trade flows between provinces, economic regions, and census divisions. When κ is significantly different from 2, the test can be interpreted as indicating that ordinary least squares is not the appropriate estimator. Source: Statistics Canada, authors' calculations. |
||||
The second step is to assess the appropriate estimator in the presence of zero flows and heteroscedastic errors. Based on Monte Carlo simulation results, Head and Mayer (2014) find that the Poisson Pseudo-Maximum-Likelihood estimator (Poisson-PML) tends to produce the least bias. Therefore, it is the preferred estimator, especially when estimates are based on flows between sub-provincial regions. It is also preferred because it perfectly replicates the Anderson and van Wincoop (2003) structural equation estimates (Fally 2015).
3.3 Geography and estimation
The analysis is based on the aggregation of point data into a set of geographic units of which the Standard-Geographic-Classification-based units (hereafter, standard geography) (for example, ERs and CDs) are just one of an almost limitless number of geographies. As demonstrated by Hillberry and Hummels (2008), estimates of barriers to trade can be strongly influenced by the geography chosen.
Hillberry and Hummels’ (2008) findings are an instance of the Modifiable Areal Unit Problem (MAUP): “. . . the sensitivity of analytical results to the definition of units for which real data are collected” (Fotheringham and Wong, 1991, p. 1025). MAUP is characterized by both a scale and zoning effect. That is, analytical results depend on the spatial resolution (scale effect) and the morphology (zoning effect) of the geography used to aggregate the data (Páez and Scott 2005).
These problems apply to multivariate statistics, including spatial interaction models like the gravity model (Fotheringham and Wong 1991, Amrhein and Flowerdew 1992 and Briant, Combes and Lafourcade 2010). In particular, Briant, Combes and Lafourcade (2010) show that gravity model results are more sensitive to scale and less sensitive to zoning effects. However, these are of secondary importance compared with model specification problems (for example, missing variable bias). Nevertheless, as Amrhein (1995) demonstrates, MAUP can emerge even when specification issues are taken into account.
Thus, the effects of geographic aggregation must be taken into account. This is accomplished by applying different geographies to the data. Two strategies are employed here. The first is to determine how sensitive the results are to the application of standard geographies, namely, defining trading regions on the basis of provinces, ERs and CDs. The second strategy takes advantage of the insight of Arbia (1989), who shows that biases resulting from the scale and zoning of the geography can be minimized by ensuring that geographic units are identical and spatially independent. A hexagonal latticeNote 6 is overlaid on the geocoded origin and destination points, creating an identical and spatially independent geography (Map 2). Hexagons that cross provincial borders are split and treated as discrete geographic units.
However, use of a hexagonal geography, while possibly minimizing the bias created by aggregating data, does not eliminate it. Issues of scale and zoning remain. Because no theoretically predetermined scale for the hexagons exists, the sensitivity of the results to size requires testing. An example is the geographic coverage of the 75 km and 225 km per side hexagons in Maps A-1 and B-1 (in Map 2). The smaller hexagons cover portions of metropolitan areas, while the larger hexagons can envelop several. Similarly, although the shape of the hexagons does not change, zoning still matters because they are arbitrarily positioned over the origin and destination points. In Map A-1, Toronto is split across two hexagons, while in Map A-2, it is split across three. Scaling and zoning effects are tested by running the model across different scales and zonings.
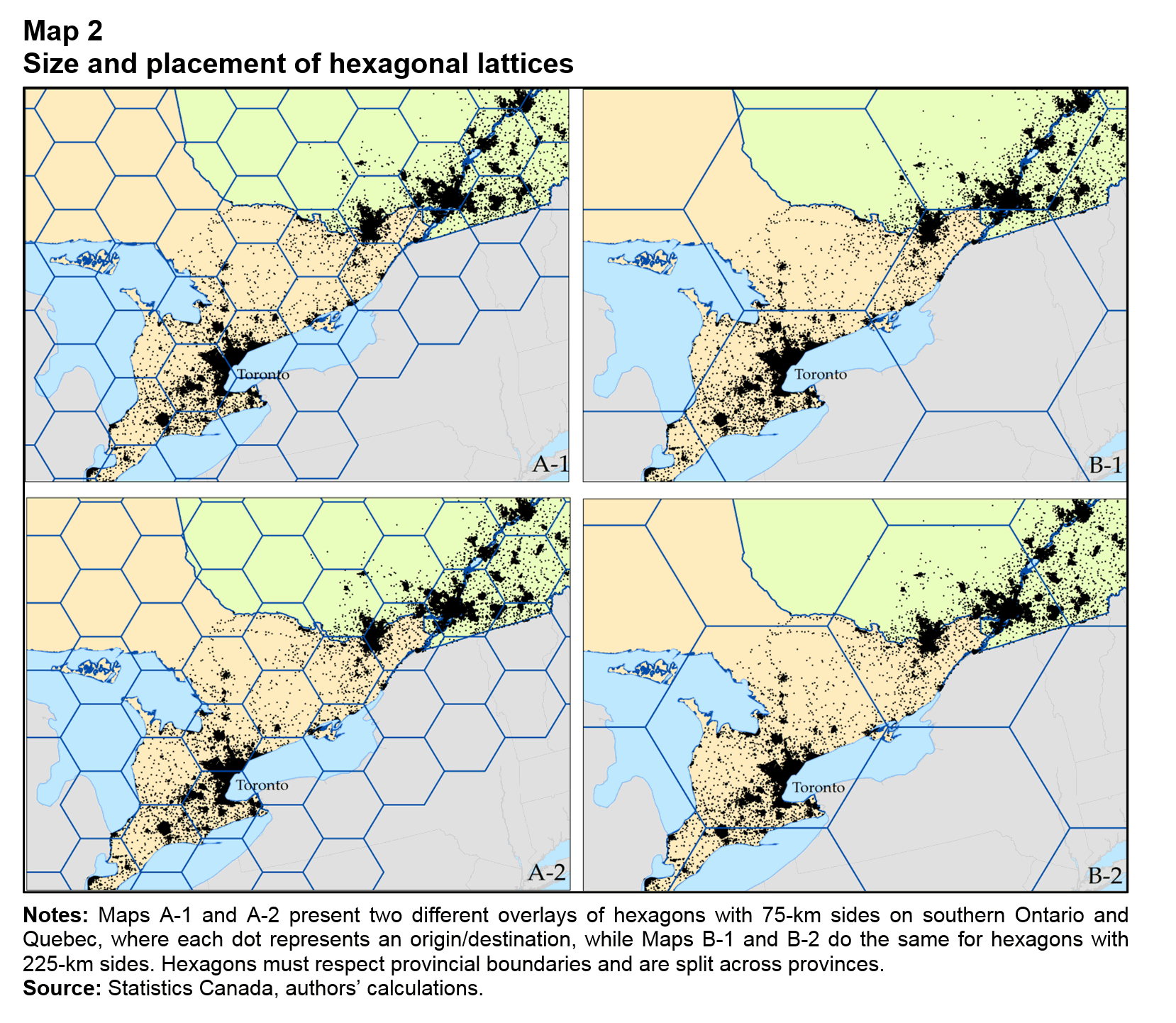
Description for Map 2
The title of Map 2 is "Size and placement of hexagonal lattices."
The map contains four maps: Map A-1, Map A-2, Map B-1 and Map B-2. Each map depicts the same area. These four maps represent the density of locations in the Surface Transportation File (STF), along with the hexagonal lattices that make up the geography in the paper.
The notes for Map 2 are as follows:
Notes: Maps A-1 and A-2 present two different overlays of hexagons with 75-km sides on southern Ontario and Quebec, where each dot represents an origin/destination, while Maps B-1 and B-2 do the same for hexagons with 225 km sides. Hexagons must respect provincial boundaries and are split across provinces.
The source of Map 2 is “Statistics Canada, authors’ calculations.”
For additional information, please contact Statistics Canada at STATCAN.infostats-infostats.STATCAN@canada.ca.
4. Model estimates
In this section, border effects are first estimated using province-level estimates of trade flows, thereby providing a base case. Border effects are then estimated using sub-provincial geographies. This forms the core of the analysis. The remainder of the discussion focuses on a set of robustness checks, with particular attention to the sensitivity of the estimates to MAUP, alternative specifications of the model, or combinations thereof.
4.1 Standard province-based estimates
Interprovincial barriers to trade are measured by comparing intraprovincial and interprovincial aggregate trade levels. This serves several purposes. First, by comparing the actual level of interprovincial trade to the benchmarked estimates, the sensitivity of the results to the loss of trade from benchmarking can be determined. Second, the OLS, Poisson-PML and Gamma-PML estimates can be compared absent zero flows. Based on their first-order conditions, the Poisson estimator puts more emphasis on the absolute deviation between actual and predicted flows, while the OLS and Gamma-PML place more emphasis on the percentage deviation, and as such, are expected to give similar results (Head and Mayer 2014). Third, the provincial results form a baseline to compare the estimated barriers to interprovincial trade using trade between sub-provincial regions.
Table 4-1 shows the estimated effects of distance and own-province on provincial trade, using the input-output-based flows and those derived after benchmarking. The model is estimated using an appropriately transformed version of (5) with the mean level of provincial trade from 2004 to 2012 as the dependent variable. Several observations may be drawn from the table.
First, estimates based on the input-output and benchmarked flows are similar. Own-province estimates tend to be lower when using the benchmarked estimates, but the effect is relatively small, particularly when the Poisson estimator is used. Because there is relatively little loss of generality resulting from the benchmarking, the remainder of the discussion focuses on these estimates.
Second, there is evidence of a border effect, regardless of estimator used. The exception is the OLS estimator, which is not significant for the benchmarked flows. Using the input-output benchmarked estimates, the border effect ranges from 1.61 (OLS) to 2.26 (Poisson)—that is, within-province trade is 61% to 126% higher than interprovincial trade when distance and multi-lateral resistance are taken into account.
A benefit of building the trade estimates up from shipment data is that it is possible to obtain a more accurate measure of the distance goods travel within and between provinces. Sensitivity of the results to the distance measure can be tested by comparing estimates based on the network distance to the great-circle distance, which is typically used in the literature (Appendix A.4).
| Network distance | ||||||
|---|---|---|---|---|---|---|
| Input-output | Benchmarked | |||||
| OLS | Poisson | Gamma | OLS | Poisson | Gamma | |
| Distance | ||||||
| Coefficient | -1.025Note ** | -0.661Note ** | -0.999Note ** | -1.077Note ** | -0.686Note ** | -1.0780Note ** |
| Standard error | 0.0458 | 0.0496 | 0.0453 | 0.0576 | 0.0522 | 0.0537 |
| Own-province | ||||||
| Coefficient | 0.607Note ** | 0.865Note ** | 0.775Note ** | 0.479 | 0.816Note ** | 0.634Note * |
| Standard error | 0.2230 | 0.0807 | 0.1900 | 0.2890 | 0.0827 | 0.2540 |
| Constant | ||||||
| Coefficient | 12.31Note ** | 9.916Note ** | 12.42Note ** | 11.70Note ** | 9.515Note ** | 12.08Note ** |
| Standard error | 0.4100 | 0.5590 | 0.3730 | 0.6300 | 0.8770 | 0.5350 |
| Border effect | 1.83 | 2.38 | 2.17 | 1.61 | 2.26 | 1.89 |
| R-squared | 0.954 | Note ...: not applicable | Note ...: not applicable | 0.959 | Note ...: not applicable | Note ...: not applicable |
| Number of observations | 100 | 100 | 100 | 100 | 100 | 100 |
... not applicable
Source: Statistics Canada, authors' calculations. |
||||||
| Great-circle distance | ||||||
|---|---|---|---|---|---|---|
| Input-output | Benchmarked | |||||
| OLS | Poisson | Gamma | OLS | Poisson | Gamma | |
| Distance | ||||||
| Coefficient | -1.058Note ** | -0.778Note ** | -1.037Note ** | -1.100Note ** | -0.806Note ** | -1.106Note ** |
| Standard error | 0.0462 | 0.0571 | 0.0436 | 0.0613 | 0.0591 | 0.0564 |
| Own-province | ||||||
| Coefficient | 0.747Note ** | 0.780Note ** | 0.840Note ** | 0.653Note * | 0.728Note ** | 0.743Note ** |
| Standard error | 0.1940 | 0.0907 | 0.1710 | 0.2740 | 0.0882 | 0.2490 |
| Constant | ||||||
| Coefficient | 12.01Note ** | 10.49Note ** | 12.17Note ** | 11.29Note ** | 10.12Note ** | 11.70Note ** |
| Standard error | 0.4050 | 0.5470 | 0.3600 | 0.6440 | 0.8480 | 0.5350 |
| Border effect | 2.11 | 2.18 | 2.32 | 1.92 | 2.07 | 2.10 |
| R-squared | 0.956 | Note ...: not applicable | Note ...: not applicable | 0.959 | Note ...: not applicable | Note ...: not applicable |
| Number of observations | 100 | 100 | 100 | 100 | 100 | 100 |
... not applicable
Source: Statistics Canada, authors' calculations. |
||||||
How distance is measured matters. On average, network distance is 33% greater than great-circle distances. As a result of the compression of distance, the parameter on distance should be more negative for great-circle distance-based estimates, which is true regardless of the estimator (see Table 4-2). As well, great-circle within-province distances are, in relative terms, overestimated (Appendix A.4), which biases the own-province effect upward. The OLS and Gamma estimators show this effect, but not the Poisson, where the bias appears to be captured by the coefficient on distance.
4.2 Estimates by sub-provincial geography
Estimates of provincial border effects based on comparisons of intraprovincial with interprovincial trade flows may still be biased, if these units do not effectively capture the pattern of trade. As shown by Hillberry and Hummels (2008), if short-distance flows predominate and are not properly captured by the internal distance measure, the estimated border effect may be biased upward.
To further establish the presence and strength of provincial border effects, intraprovincial and interprovincial trade flows are measured using sub-provincial geographies of different sizes and morphologies. Because trade can be both within and between sub-provincial geographic units, a binary variable is included for within-unit trade (own-region). It should capture non-linearities in the effect of distance for these shorter-distance flows and/or differences in the nature of own-unit versus between-region trade. Within-region trade is more likely to include short-distance flows between manufacturers and distribution centres, between distribution centres and retail stores (Hillberry and Hummels 2003), and between upstream suppliers and downstream users of intermediate inputs (Hillberry and Hummels 2008).
Moving down to sub-provincial units introduces the problem of zero flows between trading units. The set of trading units is defined as those that either make or use the good. Units that do not engage in goods trade, either within themselves or with other units, are excluded. This may result from no measurable goods production in the unit or from sampling variability. Because the estimates are based on the average value of trade over nine years, the effect of sampling variability is likely to be low. Of course, the units included in the trading set do not trade with all potential units, resulting in zero flows. Zero flows may be due to random chance (again, sampling variability), or they may be structural (producers incur costs above the trading threshold). To permit the presence of zeros, the Poisson estimator is used. For zero flows, the distance between regions is measured as the great-circle distance.Note 7
Of the four geographic units used in the analysis, two (ERs and CDs) are based on standard geographies; the other two are hexagon lattices with 75 km and 225 km per side. If hexagons were larger than 225 km per side, some of the smaller provinces would have very few. Hexagons smaller than 75 km per side would result in such a large number of fixed effects to be estimated that the Poisson-PML estimator fails to reliably converge. Table 5 displays the characteristics of the units.
| Standard | Hexagons | |||
|---|---|---|---|---|
| Economic regions |
Census divisions |
225-km sides | 75-km sides | |
| Geographic units | number | |||
| Total | 76 | 288 | 90 | 511 |
| Trading set | 73 | 282 | 90 | 380 |
| Area | square kilometres | |||
| Average | 74,930 | 19,397 | 131,528 | 14,614 |
| Standard deviation | 129,347 | 59,759 | Note ...: not applicable | Note ...: not applicable |
| Minimum | 247 | 193 | 131,528 | 14,614 |
| 25th percentile | 10,416 | 1,863 | 131,528 | 14,614 |
| Median | 20,880 | 3,771 | 131,528 | 14,614 |
| 75th percentile | 77,903 | 15,202 | 131,528 | 14,614 |
| Maximum | 747,158 | 747,158 | 131,528 | 14,614 |
| ... not applicable Notes: The trading set is defined as geographic units that engage in measured trade, excluding those in the territories. The area of sub-provincial geographic units is calculated for the trading set. Source: Statistics Canada, authors' calculations. |
||||
With ERs as the trading unit, the distance parameter tends to be less negative than the province-based estimates, with own-region likely picking up the non-linear effect of short-distance flows (Table 6). The own-province estimate is smaller, resulting in a border effect of 2.10. Using CDs—a fundamental building block of ERs—the number of potential trading pairs rises from 5,329 to 79,524. For this much larger set of smaller trading units, the border effect falls to 1.97.
For both the small and large hexagons, own-region effects were not statistically significant; the own-province effect remained significant, but notably smaller than that for standard geographies. The result is a border effect that falls in a narrow range from 1.60 (large hexagons) to 1.62 (small hexagons). In other words, intraprovincial trade is estimated to be 60% to 62% higher than interprovincial trade, all else being equal (Table 6).
| Geography | |||||
|---|---|---|---|---|---|
| Standard | Hexagon | Forward Sortation Area |
|||
| Economic region |
Census division |
225-km sides | 75-km sides | ||
| Distance | |||||
| Coefficient | -0.551Note ** | -0.573Note ** | -0.820Note ** | -0.742Note ** | -0.426Note ** |
| Standard error | 0.0461 | 0.0278 | 0.0620 | 0.0357 | 0.0146 |
| Own-region | |||||
| Coefficient | 0.408Note ** | 0.467Note ** | -0.101 | -0.0215 | 1.052Note ** |
| Standard error | 0.1380 | 0.1210 | 0.1270 | 0.1170 | 0.0966 |
| Own-province | |||||
| Coefficient | 0.743Note ** | 0.679Note ** | 0.472Note ** | 0.483Note ** | 0.909Note ** |
| Standard error | 0.0951 | 0.0633 | 0.0872 | 0.0783 | 0.0421 |
| Constant | |||||
| Coefficient | 6.981Note *** | 7.094Note *** | 3.142Note *** | 2.540Note *** | 2.015Note *** |
| Standard error | 0.4900 | 0.3590 | 0.7760 | 0.4770 | 0.3830 |
| Border effect | 2.10 | 1.97 | 1.60 | 1.62 | 2.48 |
| Number of observations | 5,329 | 77,274 | 8,619 | 132,862 | 2,574,640 |
Source: Statistics Canada, authors’ calculations. |
|||||
These results contrast with those of Hillberry and Hummels (2008), who find state border effects to be an artefact of the geography used to measure internal trade. However, in their analysis, border effects disappeared only when an even finer-grained geography than that applied here was used, namely, 5-digit ZIP codes. To account for this, the model was re-run using Forward Sortation Areas (FSAs), the closest Canadian equivalent to ZIP codes.Note 8 The point estimates for own-province remain positive and significant (Table 6), but at a higher level than the other geographies. Even with a very fine-grained geography, provincial border effects remain: a finding that is robust to a wide set of specifications (Subsection 4.3.4).
The provincial- and sub-provincial-based estimates of border effects indicate that the geography chosen matters, but information from which to draw strong conclusions is still insufficient. Two issues need to be addressed. The first is how sensitive the results are to the MAUP, namely, scaling and zoning effects (size and placement of hexagons). It is not clear if variations in provincial border effects across hexagons of different sizes (or lack thereof) are outweighed by variability resulting from the placement of the lattices. The second issue is whether a non-linear effect of distance on trade influences estimates of provincial border effects. The elasticity on distance varies across geographies and estimators, and as Head and Mayer (2014) note, variation on the distance term between the Poisson and Gamma estimators may indicate model misspecification, which is observed in Table 4. Therefore, a more rigorous assessment of how the geography and model specification, particularly non-linear effects of distance, influence estimated border effects is necessary.
4.3 Robustness of sub-provincial estimates
The robustness of the estimates is tested in four steps. The first tests how sensitive the results are to the MAUP. The second tests whether there is a non-linear effect of distance on trade that may influence estimates of provincial border effects. The third combines the first two by determining how sensitive the results are to taking both MAUP and the non-linear effect of distance into account. The fourth step returns to Hillberry and Hummel’s (2008) analysis to determine if provincial border effects remain when FSAs are used as trading units after applying their specification and estimator, as well as the fully-specified model.
4.3.1 Modifiable Areal Unit Problem
To test the sensitivity of the results to the MAUP, the models are re-run on randomly shifted hexagonal lattices of varying sizes. For a given size of hexagon, the lattice is superimposed on Canada’s landmass, with each origin and destination point coded to their respective province and hexagon. The centroid of each hexagon is then shifted to any random point within a circle circumscribed by its borders. The set of points is limited to the circumscribed circle, because shifting over more than one unit simply repeats the pattern. The origin and destination points are recoded to their province and hexagon. The lattice is randomly shifted 100 times,Note 9 resulting in a set of parameters that describes how sensitive the estimates are to the placement of the lattice (MAUP zoning effect) for a given size of hexagon. This is repeated for seven sizes, increasing in 25 km per side increments from 75 km to 225 km. This accounts for how sensitive the results are to the size of hexagons (the MAUP scaling effect).
To represent the distribution of coefficients resulting from the simulations for the main variables—own-province, own-region (hexagon) and distance—Figure 3 presents box plots by size of hexagon. The boxes represent the interquartile range, with the line intersecting the box being the median coefficient value. The ends of the whiskers—upper and lower adjacent values—represent the ranked coefficient value nearest to, but not above/below 1.5 times, the interquartile range from above/below. The dots identify extreme values.

Description for Figure 3
The title of Figure 3 is "Coefficient estimates for own province, own region, and distance by size (kilometre per side) and placement of hexagons."
There are 3 box-and-whisker plots of regression coefficient estimates in this figure.
The horizontal axis of each plot has 7 categories: 75, 100, 125, 150, 175, 200 and 225.
The vertical axis of the first plot is "Coefficient: Own province." It starts ad 0.35 and ends at 0.55, with tick marks every 0.05.
The median value of the first plot for category 75 is 0.5, the median value for category 225 is 0.45, with the other median values being in between these two.
The vertical axis of the second plot is "Coefficient: Own region." It starts at -0.4 and ends at 0.2, with tick marks at every 0.2.
The median value of the second plot for category 75 is about -0.15, the median value for category 225 is about -0.05, with the other median values being in between these two. The upper whisker on each category in the second plot is above 0.
The vertical axis of the third plot is "Coefficient: Distance." It starts at -0.9 and ends at -0.7, with tick marks at every 0.05.
The median value of the third plot for category 75 is about -0.75, the median value for category 225 is about -0.82, with the other median values being in between these two.
The notes for Figure 3 are as follows:
Notes: The boxes represent the interquartile range, with the line intersecting the box being the median coefficient value. The ends of the whiskers—the upper and lower adjacent values—represent the ranked coefficient value that is nearest to but not above (below) 1.5 times the interquartile range from above (below). The dots signify extreme values.
The source for Figure 3 is “Statistics Canada, authors’ calculations.”
For additional information, please contact Statistics Canada at STATCAN.infostats-infostats.STATCAN@canada.ca.
For own-province, the median coefficient values range from 0.50 for the smallest hexagons to 0.45 for the largest (scaling effect), with the coefficients asymptotically converging toward the lower median value as the size of hexagons increases. This is consistent with Coughlin and Novy (2016), who report that if trade within small units is particularly strong, as the size of the unit increases, the border effect tends to diminish. Placement of the hexagonal lattice (zoning effect) has a larger effect on the estimates, with the difference between the box plot lower and upper adjacent values being greater than the difference in the medians across the size of hexagons. This contrasts with Briant, Combes and Lafourcade (2010), who find the scaling effect is more important. More broadly, shifting to a uniform geography has a qualitative effect on the estimated border effect, a result that holds when accounting for the effect of the size and placement of the hexagons on the estimates.
4.3.2 Non-linear effects of distance
Variation in the results across hexagons of different sizes may stem from a non-linear effect of distance on trade, a telltale sign of which is the negative effect of hexagon size on the distance coefficient (Figure 3). As the hexagons become smaller, the average distance shipped decreases. If these more prevalent shorter-distance flows are underestimated, the provincial border effect will be overestimated, because intraprovincial trade occurs over shorter distances than interprovincial trade (Figure 2). This appears to be the case, as a positive association exists between the own-province and the distance coefficients (Figure 3).
For at least two reasons, the effect of distance on trade is expected to vary. First, prices charged by trucking firms, for instance, include fixed and variable (line-haul) cost components. Because fixed costs per shipment are around $200 and line-haul costs increase at about $0.80 per kilometre (Brown 2015), prices inclusive of transport costs will effectively be uniform over short distances. Second, the endogenous clustering of upstream suppliers and downstream firmsNote 10 and hub-and-spoke distribution networksNote 11 (Hillberry and Hummels 2008) may result in a large volume of trade over short distances, with a steep drop as distance shipped moves beyond “just down the street” shipments. Uniform prices over short distances, combined with clustering/distribution effects, result in a complicated set of expectations. For very short distance flows, the effect of distance on trade may be negative (at least after a short plateau), but the negative effect of distance on trade beyond these very short distance flows is expected to be initially weak, but stronger as variable costs surpass the effect of fixed costs on transportation rates. This pattern in the data requires moving beyond the standard quadratic form to account for non-linearities.
To account for the non-linear effects of distance, the model is re-estimated using a spline with knots at 25 km, 100 km and 500 km (Table 7) employing the hexagonal lattices for the estimates in Table 6.Note 12 Based on the smaller hexagon results, the distance elasticities are consistent with a steep drop in shipments over very short distances (reflecting co-location of input-output linked plants, for instance), while the insignificant effect of distance for 25 to 100 km flows is consistent with a relatively constant transportation rate charged by firms over short distances. Accounting for the non-linear effect of distance causes the coefficient on own-province to become more similar across hexagon size classes. However, given the sensitivity of the results to placement of the hexagonal lattices, from this single set of point estimates, it is unclear how similar the border effect estimates are between the large and small hexagons.
Finally, a binary variable is added for hexagons that share a border (contiguous regions). The expectation is that this contiguity measure will account for short-distance flows across boundaries. For both the large and small hexagons, the contiguous region coefficient is insignificant, but the own-province coefficient falls while remaining significant.
| Hexagon: 225-km sides | Hexagon: 75-km sides | |||
|---|---|---|---|---|
| Model 1 | Model 2 | Model 1 | Model 2 | |
| Distance | ||||
| 0 km to 25 km | ||||
| Coefficient | -1.356Note ** | -1.338Note ** | -0.932Note ** | -0.923Note ** |
| Standard error | 0.284 | 0.281 | 0.122 | 0.122 |
| 25 km to 100 km | ||||
| Coefficient | -0.544 | -0.561 | -0.268 | -0.276 |
| Standard error | 0.471 | 0.469 | 0.227 | 0.227 |
| 100 km to 500 km | ||||
| Coefficient | -0.836Note ** | -0.720Note ** | -0.711Note ** | -0.801Note ** |
| Standard error | 0.1190 | 0.1200 | 0.0598 | 0.0915 |
| Greater than 500 km | ||||
| Coefficient | -0.818Note ** | -0.772Note ** | -0.862Note ** | -0.858Note ** |
| Standard error | 0.0854 | 0.1090 | 0.0684 | 0.0689 |
| Own-region | ||||
| Coefficient | -0.0608 | 0.2330 | 0.312Table 7 Note † | 0.1790 |
| Standard error | 0.173 | 0.237 | 0.161 | 0.199 |
| Own-province | ||||
| Coefficient | 0.458Note ** | 0.412Note ** | 0.431Note ** | 0.418Note ** |
| Standard error | 0.0839 | 0.0755 | 0.0713 | 0.0709 |
| Contiguous regions | ||||
| Coefficient | Note ...: not applicable | 0.195 | Note ...: not applicable | -0.132 |
| Standard error | Note ...: not applicable | 0.1380 | Note ...: not applicable | 0.0972 |
| Constant | ||||
| Coefficient | 4.513Note ** | 4.184Note ** | 2.638Note ** | 2.746Note ** |
| Standard error | 0.807 | 0.833 | 0.494 | 0.501 |
| Border effect | 1.58 | 1.51 | 1.54 | 1.52 |
| Number of observations | 8,619 | 8,619 | 132,862 | 132,862 |
... not applicable
Source: Statistics Canada, authors' calculations. |
||||
4.3.3 Non-linear effects of distance and the Modifiable Areal Unit Problem
The next check assesses whether accounting for the non-linear effects of distance reduces the degree of variation in results across different sizes and placement of hexagons. Again, this is accomplished by randomly perturbing the hexagonal lattices for the largest (225 km per side) and smallest (75 km per side) hexagons, and also, across model specifications. The “base” model estimates replicate those in Figure 3 (which uses the specification in Table 6); Model 1 and Model 2 match those in Table 7. Taking the non-linear effect of distance into account reduces the median coefficient of the small hexagons, but increases that of the large hexagons (Figure 4), effectively reversing the pattern in Figure 3. Adding contiguity to the model (Model 2) produces large and small hexagon-based provincial border effects that are statistically indistinguishable. The coefficients on own hexagons also converge, but only when contiguity is taken into account. While the central tendencies of the small and large hexagon coefficient distributions are the same, their variances are not—the large hexagons have more than double the interquartile range of the small hexagons. On this basis, the small-hexagon border effects are the most reliable.
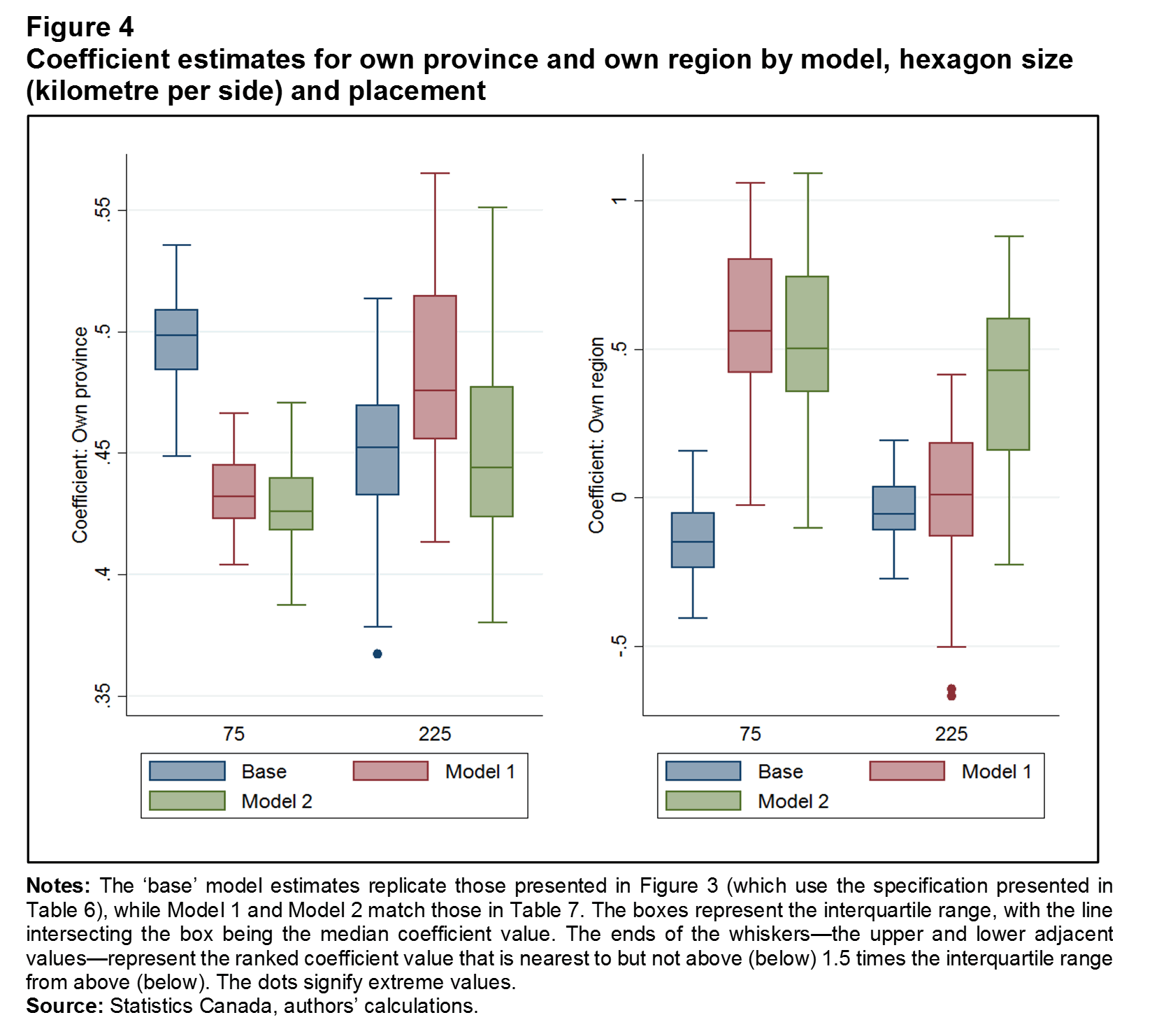
Description for Figure 4
The title of Figure 4 is "Coefficient estimates for own province and own region by model, hexagon size (kilometre per side) and placement."
There are two box-and-whisker plots of regression coefficient estimates in this figure.
The horizontal axis of each plot has two categories: 75 and 225.
Each category in each plot has three series: series 1 is labeled "Base," series 2 is labeled "Model 1," and series 3 is labeled "Model 2."
The vertical axis of the first plot is "Coefficient: Own province."
In the first plot, the median values for the three series at category 75 are as follows: series 1, 0.5; series 2, around 0.44; series 3, around 0.43.
In the same plot, the median values for the three series at category 225 are as follows: series 1, 0.45; series 2, around 0.47; series 3, around 0.45.
The vertical axis of the second plot is "Coefficient: Own region."
In the second plot, the median values for the three series at category 75 are as follows: series 1, -0.1; series 2, around 0.5; series 3, around 0.5.
In the same plot, the median values for the three series at category 225 are as follows: series 1, around -0.1; series 2, around 0.0; series 3, around 0.45.
The notes for Figure 4 are as follows:
Notes: The ‘base’ model estimates replicate those presented in Figure 3 (which use the specification presented in Table 6), while Model 1 and Model 2 match those in Table 7. The boxes represent the interquartile range, with the line intersecting the box being the median coefficient value. The ends of the whiskers—the upper and lower adjacent values—represent the ranked coefficient value that is nearest to but not above (below) 1.5 times the interquartile range from above (below). The dots signify extreme values.
The source of Figure 4 is “Statistics Canada, authors’ calculations.”
For additional information, please contact Statistics Canada at STATCAN.infostats-infostats.STATCAN@canada.ca.
4.3.4 Provincial border effects based on Forward Sortation Areas
As a last robustness check, the analysis revisits Hillberry and Hummels’ (2008) finding that state border effects are eliminated when trade is measured using five-digit ZIP codes. This entails initially using the estimator (OLS) and model specification (quadratic term on distance) in their analysis, and then applying the preferred estimator (Poisson) and model (distance effects estimated using a spline) used above.
While the model and estimators can be equated, results may vary because of differences in the underlying data. First, because Hillberry and Hummels’ (2008) CFS data are shipper-based, shipments can be limited to those of manufacturers, rather than wholesalers and distributors. However, the data used here are carrier-based, so it is not possible to distinguish between the two. To the extent that shipments from wholesalers are more localized, stronger trade is more likely at short distances, which should be accounted for by the own-region (FSA) term.
Second, because the estimates are based on the nine-year average of flows across FSAs, a fuller set of flows is likely to be obtained than that provided by the CFS. As a result of this and of Canada’s geography, the FSA data are weighted toward longer-distance flows, with the average distance shipped between FSAs being 1,679 km (1,049 miles), whereas the average distance between ZIP codes is 837 km (523 miles) (Hillberry and Hummels 2008). Because distance elasticity increases (in absolute terms) with distance shipped, the effect of distance is expected to be stronger in the present analysis.
Table 8 contains the estimates, with the first three columns showing the model equivalent to that in Hillberry and Hummels (2008, Table 2). The first column contains OLS-based estimates; the second and third, Poisson-based estimates without and with zeros included, respectively. Evaluating the effect of distance using the mean distance of 837 km, elasticity is -0.42, more than double the ZIP-code-based estimate of -0.19. Also, the point estimate for own-region (FSA) is much higher. These disparities were expected, given the differences in the underlying data. Specifically, the own-province effect is positive and significant when using the same estimator, model and geography as Hillberry and Hummels.
Application of the Poisson estimator reduces the effect of distance, because larger (typically) short-distance flows are weighted more heavily. Evaluated at 837 km, elasticity on distance is -0.25, and only slightly lower in absolute terms when zero flows are added. The Poisson estimator also produces smaller, but still significant, own-region and own-province effects. Inclusion of zero flows results in a positive coefficient on distance up to 5 km, and a declining point estimate thereafter. Adding zeros also raises the point estimates on own-region and province. The highly non-linear effect of distance when the Poisson estimator is applied suggests that the influence of distance on trade has to be treated in a flexible manner. This is accomplished by estimating a spline on distance.
| OLS | Poisson | |||||
|---|---|---|---|---|---|---|
| Model 1 | Model 1 | Model 2 | Model 3 | Model 4 | ||
| Distance | ||||||
| Coefficient | -0.490Note ** | -0.0105 | 0.217Note ** | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Standard error | 0.0220 | 0.0517 | 0.0566 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Distance squared | ||||||
| Coefficient | 0.0104Note ** | -0.0353Note ** | -0.0661Note ** | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Standard error | 0.00178 | 0.00446 | 0.00479 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Distance | ||||||
| 0 km to 25 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | -0.0678 | Note ...: not applicable | Note ...: not applicable |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.0587 | Note ...: not applicable | Note ...: not applicable |
| 0 km to 10 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.303Note ** | Note ...: not applicable |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.110 | Note ...: not applicable |
| 0 km to 5 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.542Note * |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.245 |
| 5 km to 10 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.0223 |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.3470 |
| 10 km to 25 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | -0.461Note ** | -0.393Note ** |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.116 | 0.131 |
| 25 km to 100 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | -0.296Note ** | -0.198Note ** | -0.206Note ** |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.0668 | 0.0669 | 0.0667 |
| 100 km to 500 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | -0.497Note ** | -0.507Note ** | -0.505Note ** |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.0377 | 0.0374 | 0.0375 |
| Greater than 500 km | ||||||
| Coefficient | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | -0.767Note ** | -0.764Note ** | -0.764Note ** |
| Standard error | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable | 0.0235 | 0.0235 | 0.0235 |
| Own-region | ||||||
| Coefficient | 2.357Note ** | 1.316Note ** | 1.494Note ** | 1.472Note ** | 1.561Note ** | 1.551Note ** |
| Standard error | 0.1040 | 0.1010 | 0.1010 | 0.1040 | 0.0998 | 0.1010 |
| Own-province | ||||||
| Coefficient | 1.211Note ** | 0.468Note ** | 0.616Note ** | 0.592Note ** | 0.592Note ** | 0.593Note ** |
| Standard error | 0.0154 | 0.0361 | 0.0385 | 0.0393 | 0.0393 | 0.0393 |
| Constant | ||||||
| Coefficient | -3.117Note ** | 1.618Note ** | 1.123Note ** | 1.416Note ** | 0.793Table 8 Note † | 0.551 |
| Standard error | 0.217 | 0.399 | 0.408 | 0.415 | 0.442 | 0.472 |
| Number of observations | 652,214 | 652,214 | 2,574,640 | 2,574,640 | 2,574,640 | 2,574,640 |
| Border effect | 3.36 | 1.60 | 1.85 | 1.81 | 1.81 | 1.81 |
| Distance elasticity at 837 km | -0.42 | -0.25 | -0.23 | Note ...: not applicable | Note ...: not applicable | Note ...: not applicable |
| Includes zero flows | no | no | yes | yes | yes | yes |
... not applicable
Source: Statistics Canada, authors' calculations. |
||||||
Model 2 uses the same structure as Model 1 in Table 7, with knots at 25 km, 100 km and 500 km. The provincial border effect is lower than when the quadratic is used on distance, but remains significant. Unlike when hexagons are used, no strong negative effect on distance is evident between 0 and 25 km. Instead, because the vast majority of FSAs are small and located in metropolitan areas, the effect of short-distance flows is captured by the own-region term, with a strong positive coefficient. Hexagons, whose size distribution is not associated with the density of short-distance flows, have a weaker relationship. Further subdividing the effect of distance over short-distance shipments reveals a positive association with distance between 0 and 10 km (Model 3) and between 0 and 5 km (Model 4). At such short distances, increases in distance have little effect on trade costs, but an apparent increase in the number of potential sources of demand. The estimated provincial border effect is unchanged with these changes to the specification. In short, contrary to Hillberry and Hummels (2008), adoption of very small trading units does not eliminate border effects. Therefore, provincial border effects, while sensitive to the specification and the geography, are never eliminated. However, the question of whether they are economically meaningful remains.
5. Border effect tariff equivalent
To estimate the tariff equivalent of the provincial border effect, Head and Mayer’s (2014, p. 32–34) approach is applied. As above, denotes the provincial border effect coefficient, which reflects the reduction in trade costs between sub-provincial regions simply by virtue of being part of the same province. Given that , where and are interprovincial and intraprovincial trade costs, respectively, and is the trade elasticity with respect to transportation costs, if is the tariff that must be removed to equate the cost of moving goods within and between provinces, the interprovincial trade tariff equivalent is
where is the tariff equivalent of within-province barriers to trade, which are assumed to be zero. Hence, the only missing information is the trade cost elasticity of trade:
where is 1 plus the ad valorem transportation costs, and are, respectively, origin and destination fixed effects, and is the error term. Ad valorem transportation costs are derived from the STF, which reports the price charged to shippers and the estimated value of each shipment. EstimatedNote 13 price elasticity based on (8) is -6.40, which is between the median (-5.03) and average (-6.74) price elasticities identified in Head and Mayer’s (2014) meta-analysis.
For the median provincial border effect coefficient on the 75 km per side hexagon (Figure 4, Model 2), or 6.9%. Using a different methodology, Agnosteva, Anderson and Yotov (2014) arrive at a lower, but statistically indistinguishable,Note 14 estimate of 5.6%.
The tariff equivalents of the border effect across the standard and hexagonal geographies are presented in Chart 1 and illustrate the impact of the trading unit chosen. The hexagons use the median point estimates from the simulations in Figures 3 and 4. The provincial estimates are the highest at 13.6%, followed closely by ER- and CD-based tariff equivalents of 12.3% and 11.2%, respectively. Imposition of a uniform hexagonal geography causes the most notable drop in the tariff rate. As the hexagons become larger, the point estimates converge to a tariff equivalent of 7.3%. The tariff equivalent for the 75 km and 225 km per side hexagons that accounts for the non-linear effect of distance and contiguity (Figure 4, Model 2) provides the lowest estimates, which are essentially indistinguishable. Therefore, in the fully specified model, the size of hexagon chosen is of little consequence. At 6.9%, the 75 km per side hexagons provide the preferred estimate, because of the smaller interquartile range relative to the 225 km per side hexagons. Compared with this estimate, relying on provincial trade would increase border effect estimates by 6.7 percentage points, a substantial difference. To put it in perspective, this value is above Canada’s mean tariff rate (4.9%).Note 15

Data table for Chart 1
| Tariff equivalent | |
|---|---|
| value | |
| Standard geography | |
| Province | 13.6 |
| Economic region | 12.3 |
| Census division | 11.2 |
| Hexagon (kilometre per side) | |
| 75 | 8.1 |
| 100 | 7.6 |
| 125 | 7.4 |
| 150 | 7.4 |
| 175 | 7.3 |
| 200 | 7.4 |
| 225 | 7.3 |
| Hexagon with spline (kilometre per side) | |
| 75 | 6.9 |
| 225 | 7.2 |
|
Notes: All tariff equivalents are estimated using a price elasticity on transportation costs of -6.40. The standard geography ad valorem tariff equivalents are based on the provincial border effect estimates from Table 4 (Poisson estimate of the benchmarked flows using the network measure of distance) and Table 5. The hexagon-based tariff equivalents are based on the median point estimate from Figure 5, while the hexagon with spline-based tariff equivalents are the median point estimate from Figure 6 based on Model 2 from Table 7, which includes the control for contiguous regions. Source: Statistics Canada, authors' calculations. |
|
| Commodity | Tariff equivalent |
|---|---|
| coefficient | |
| Grains and other crop products | 0.07Note * |
| Live animals | 0.09Note * |
| Fish and seafood, live, fresh, chilled or frozen | -0.01 |
| Other farm products | 0.14Note * |
| Forestry products and services | 0.32 |
| Metal ores and concentrates | -0.23Note * |
| Non-metallic minerals | 0.09 |
| Alcoholic beverages and tobacco products | 0.01 |
| Food and non-alcoholic beverages | 0.04Note * |
| Textile products, clothing, and products of leather and similar materials | 0.04Note * |
| Wood products | 0.12Note * |
| Wood pulp, paper and paper products and paper stock | 0.20Note * |
| Printed products and services | 0.07Note * |
| Refined petroleum products (except petrochemicals) | 0.02Note * |
| Chemical products | 0.02 |
| Plastic and rubber products | 0.08Note * |
| Non-metallic mineral products | 0.24Note * |
| Primary metallic products | 0.06Note * |
| Fabricated metallic products | 0.08Note * |
| Industrial machinery | 0.02Note * |
| Computer and electronic products | 0.01 |
| Electrical equipment, appliances and components | 0.02Note * |
| Motor vehicle parts | 0.11Note * |
| Transportation equipment | 0.03Note * |
| Furniture and related products | 0.08Note * |
| Other manufactured products and custom work | 0.05Note * |
Source: Statistics Canada, authors' calculations. |
|
The tariff equivalent of the border effect by commodity is calculated by estimating by commodity the border effect and the elasticity of trade with respect to transportation costs . The statistical significance of the border effect is reported alongside the tariff equivalent (see Table 9). The border effect is small and statistically insignificant for many commodities, including transportation equipment, industrial machinery and refined petroleum products. For others that are largely intermediate goods (for example, motor vehicle parts), an apparent border effect is evident, potentially reflecting variation in industrial demand across provincial borders. For instance, most demand for auto parts comes from assembly plants concentrated in Ontario. However, for other commodities, there may be some aggregation bias. No significant border effect exists for alcoholic beverages and tobacco products, but this stems largely from the inclusion of tobacco products. When disaggregated, the expected pattern emergesthe tariff equivalents for distilled liquor, wine and brandy, and beer are 8%, 56%, and 2%,Note 16 respectively. Dairy products might be viewed in the same way, but the commodity aggregations in the trucking data are too broad to separate flows of dairy products to accurately estimate the border effect.
6. Conclusions
Because of a lack of geographically detailed data on trade within and across provinces, intra-national border effects are difficult to measure. By using a new flexible transaction-level transportation data file to generate regional trade flows within and across provincial borders, this analysis shows that regardless of the model or geography chosen, provincial border effects persist, with an implied ad valorem tariff equivalent of 6.9%. This contrasts with estimates for the United States, in which state border effects are eliminated when similar approaches are applied. While the presence of provincial border effects is consistent with a dampening influence of non-tariff barriers on interprovincial trade, they do not, in and of themselves, account for all barriers, because border effects capture multiple factors that affect interprovincial trade.
Several methods-based observations may be drawn from this analysis. First, while the results are sensitive to the size of geographic unit chosen (province, economic region, census division or hexagon), a simple linear relationship does not exist between (average) size and border effects. In fact, a uniform shape (hexagons) is more important than the size of the geographic unit. This supports Arbia’s (1989) finding that biases resulting from the scale and zoning of the geography are minimized by using identical units.
Second, accounting for the non-linear effect of distance is as or more important than controlling for geography (the Modifiable Areal Unit Problem [MAUP]). The negative association between hexagon size and border effects stemming from a non-linear relationship between distance and trade predicted by Coughlin and Novy (2016) is effectively eliminated when these non-linearities are explicitly taken into account. Nonetheless, accounting for MAUP is useful, as it provides a means to test the model’s specification.
Further work is needed to identify the effect of provincial non-tariff barriers on estimated border effects, because direct information is required on the extent of these barriers and on other factors that influence interprovincial trade (for instance, firm linkages and migratory flows across provincial borders). Furthermore, while this analysis was able to estimate provincial border effects, the overall welfare implications resulting from their elimination are not measured here. Nevertheless, as Albrecht and Tombe (2016) show, these can be substantial.
Appendix A Data appendix
A.1 Valuing shipments
The waybills on which the Surface Transportation File (STF) is based describe the commodity and tonnage of each shipment, but not its value. To estimate value, a measure of the value per tonne is required. This is derived from an experimental transaction-level trade file that measures the value and tonnage of goods by detailed Harmonized Commodity Description and Coding System (HS) commodity in 2008. Because the trade file identifies the mode used for each shipment, the value per tonne for each commodity also varies by the mode used. Export prices indices are used to project the value per tonne estimates through time (see Brown [2015] for a detailed discussion).
A.2 Geocoding shipment origins and destinations
Based on postal code data from the Trucking Commodity Origin and Destination Survey (TCOD) and Standard Point Location Codes (SPLCs) from the rail waybill file, each shipment is geocoded (assigned a latitude and longitude for the origin and destination) from 2004 to 2012. These are used to give the file a 2006 Standard Geographic Classification (Statistics Canada, n.d.b). As a result, each origin and destination is coded to its economic region (ER), census division (CD) and consolidated census subdivision (CCSD). Before 2004, the TCOD did not use postal codes to identify origins and destinations. For these years, the flows are coded only to ERs. Because origins and destinations are given latitudes and longitudes, other non-standard geographies can be applied, such as the hexagonal lattices in this analysis. Imputation of just over half the postal codes likely reduces their accuracy. Nevertheless, when mapped, imputed and non-imputed postal codes presented similar geographic patterns.
A.3 Benchmarked weights
A primary goal when constructing the file is to ensure that value of trade on a shipment basis in the STF adds to known trade totals by commodity from the interprovincial trade flow file. To do this, two problems must be overcome, because the files represent different trade concepts and use different commodity classifications.
In the interprovincial trade flow file, an origin represents the point of production, and a destination represents a point of consumption. However, in the STF, an origin represents the point at which the shipment is picked up, and the destination is the point at which the shipment is dropped off, including warehouses that are transportation waypoints. A commodity produced in Quebec and consumed in British Columbia would be recorded as a flow from Quebec to British Columbia in the interprovincial trade flow database, but that flow may have multiple sources and destinations in the STF if it stops at warehouses in different provinces along the way. For instance, a Quebec-to-British Columbia trade flow might be counted as flows from Quebec to Ontario, and then from Ontario to British Columbia. This results in the STF overestimating flows between close provinces and underestimating flows between provinces that are farther apart, potentially biasing border effect estimates upward. Benchmarking is an attempt to re-weight the surface transportation shipments to reflect the interprovincial trade flow concept.
The two files use related, but in practice, different, commodity classification systems. Although both commodity classifications are built from the commodity-based HS, the resulting aggregate classifications are so different as to eliminate any one-to-one matching between them. The STF uses the Standard Classification of Transported Goods (SCTG) (Statistics Canada, n.d.a), while the interprovincial trade flow file uses the Input-Output Commodity Classification (IOCC). At every level of aggregation, some SCTG codes map to multiple IOCC codes, and vice versa. Because of the large number of multiple matches, no attempt is made to force a single IOCC code to any SCTG code. Instead, the goal is to benchmark the transportation file so that it represents the same values as the interprovincial flow file without specifying which transported commodities represent which input-output commodities. Rather than forcing a one-to-one concordance between the files, the benchmark weights are set such that flows add to total commodity flows generated by the input-output system. The process involves a series of steps.
In the first step, each file is aggregated to include values of flows by year, origin province, destination province and commodity (SCTG for the STF; IOCC for the interprovincial flow file). This generates two vectors of the value of trade for IOCC commodity flows and SCTG commodity flows: and , respectively.
The second step builds a concordance between SCTG and IOCC by province pair and year. This is done through one-to-many mappings from SCTG to HS and from IOCC to HS, which combine to form a many-to-many map from SCTG to IOCC, creating a concordance matrix used in the third and final step.
In the final step, the benchmark weights are calculated. For each year and origin and destination province pair, the two commodity vectors, and , are combined with the concordance matrix , of which all values are either 0 or 1 (depending on whether a given SCTG commodity maps to a given IOCC commodity). Defining the number of IOCC commodities as and the number of SCTG commodities as , then has length , has length , and is an matrix. The benchmarking problem can be written:
Where is the matrix of benchmarking values, and is the element-wise matrix product (Hadamard product). Any that solves this system of equations will benchmark to . The problem is to find a solution to equations given unknowns. A typical solution is to force to be one-to-one, such that if , then for all and for all , where and index elements of . In that way, the matrix has only non-zero values, and the benchmark weight is . In this case, the concordance would be static; there would be no need to undertake a concordance by year, let alone province pair. However, this approach discards considerable amounts of information about underlying trading relationships between provinces, because the commodity profile of trade varies across province pairs. For instance, the commodity in a forced pairing may not be found in the trade between the two provinces. Hence, the benchmarking concordance should reflect, and indeed, take advantage of those differences.
To preserve information in the face of a particularly severe many-to-many concordance problem in , each element of is separated into two parts, , where
Equation (9) is simply the product of the trade shares of the concorded SCTG- and IOCC-based flows. It is assumed that the SCTG- and IOCC-based flows are an accurate representation of the patterns of trade and so provide appropriate splits against which to benchmark. is the value that solves the equation
for each equation in the system, with the convention that if or the sum on the left-hand side of (10) is zero. The only remaining issue is to calculate a single benchmark value for one SCTG code given by
which is considered the benchmark weight for all shipments of SCTG commodity in that year and province origin–destination pair. In other words, is the sum of the values of column of .
Again, any that solves this equation will be a benchmark, but the choice is to maximize the information available. Specifically, is chosen to use the value of an SCTG commodity flow relative to the total SCTG flows that point to the same IOCC code , and also the value of the flow of that IOCC code relative to all of the IOCC codes that are pointed at by SCTG commodity . In addition, although two commodities cannot be compared directly, the total value of benchmarked trade is the same as the total value of interprovincial trade (for each year-province-province observation), because
Hence, the procedure achieves the goal of ensuring that trade flows add to known totals from the provincial accounts.
In some instances, the sample of shipments will not cover all the SCTG commodities between two provinces in a year (Figure 1 in Subsection 2.1). In this case, for some IOCC commodity , the -th element of the vector is zero, because for all the possible commodities that map to (those for which ). In this case, the element is included in total interprovincial trade, but the corresponding is zero on the right-hand side, which means that total trade in the STF is less than total trade in the interprovincial flows,
Finally, in the main body of the text, the subscript is suppressed such that the benchmark weight is .
A.4 Comparing network and great-circle intraprovincial and interprovincial distances
The analysis relies on the network distance between geocoded origins and destinations, which is the average of transaction-level intraprovincial and interprovincial distances. Traditionally, intraprovincial and interprovincial distances are measured using the origin–destination population-weighted great-circle distance (hereafter, great-circle distance) between sub-provincial units (see, for example, Brown and Anderson 2002). This is calculated for the set of sub-provincial units (CDs) within each province for intraprovincial trade and between the sets of sub-provincial units for each province pair:
Where and index provinces, and index CDs, is the population of the CD, and is the great-circle distance between the centroids of CDs. For intraprovincial trade , within-CD distance is the radius of a circle of an area equal to that of the CD: .
It might be assumed that network distance always exceeds great-circle distance. However, because the actual (network) distance travelled is skewed toward short-distance trips, when short-distance trips are more prevalent (for example, intraprovincial trade or trade between contiguous provinces), measured network distance may be shorter. That is, for the great-circle distance, holding population constant, the distance between nearer CD pairs is weighted the same as between more distant CD pairs. Because they are derived from actual trips, the network distance estimates will weigh closer CD pairs more highly.
This pattern is evident in the data in Table A.1, which presents the network and great-circle distance within and between provinces. On average, network distance is 33% greater than great-circle distance. However, this is the tendency for intraprovincial distances and distances between contiguous provinces to be closer to (or even less than) the network distance. For within province, contiguous province, and non-contiguous provinces, network distance is 9%, 25% and 38% greater than great-circle distance, respectively. The exceptions are the Atlantic Provinces, which form a de facto archipelago whose internal network distances quite naturally exceed great-circle distances by a wide margin (Table A.1).
Two implications for the econometric analysis follow from these distance patterns. First, because great-circle distance is less than network distance, elasticity on distance will be less when network distance is used. Second, the relatively shorter intraprovincial great-circle distances will tend to inflate the intraprovincial trade coefficient (border effect), because of the overestimated intraprovincial trade given the actual distance travelled. Both effects are apparent in the estimates.
| N.L. | P.E.I. | N.S. | N.B. | Que. | Ont. | Man. | Sask. | Alta. | B.C. | |
|---|---|---|---|---|---|---|---|---|---|---|
| kilometres | ||||||||||
| Panel A—Network distance | ||||||||||
| Newfoundland and Labrador | 386 | 1,364 | 1,226 | 1,344 | 1,567 | 2,789 | 4,650 | 5,223 | 6,074 | 6,902 |
| Prince Edward Island | 1,412 | 61 | 333 | 272 | 1,115 | 1,706 | 3,584 | 4,209 | 4,810 | 5,696 |
| Nova Scotia | 1,326 | 324 | 136 | 389 | 1,173 | 1,815 | 3,616 | 4,308 | 4,977 | 5,802 |
| New Brunswick | 1,359 | 240 | 396 | 153 | 692 | 1,357 | 3,293 | 3,946 | 4,588 | 5,307 |
| Quebec | 1,478 | 1,095 | 1,222 | 728 | 280 | 584 | 2,459 | 3,114 | 3,734 | 4,607 |
| Ontario | 2,818 | 1,730 | 1,819 | 1,456 | 599 | 191 | 2,026 | 2,798 | 3,429 | 4,320 |
| Manitoba | 4,573 | 3,526 | 3,627 | 3,236 | 2,410 | 1,707 | 213 | 654 | 1,340 | 2,207 |
| Saskatchewan | 5,249 | 4,127 | 4,322 | 3,929 | 3,118 | 2,692 | 621 | 221 | 683 | 1,570 |
| Alberta | 5,806 | 4,907 | 4,908 | 4,578 | 3,720 | 3,248 | 1,316 | 660 | 219 | 905 |
| British Columbia | 6,873 | 5,750 | 5,872 | 5,476 | 4,640 | 4,283 | 2,244 | 1,631 | 1,010 | 204 |
| Panel B—Great-circle distance | ||||||||||
| Newfoundland and Labrador | 261 | 715 | 762 | 894 | 1,407 | 1,987 | 3,056 | 3,539 | 4,056 | 4,717 |
| Prince Edward Island | 715 | 39 | 193 | 211 | 756 | 1,322 | 2,547 | 3,071 | 3,621 | 4,274 |
| Nova Scotia | 762 | 193 | 143 | 290 | 805 | 1,344 | 2,635 | 3,167 | 3,723 | 4,374 |
| New Brunswick | 894 | 211 | 290 | 140 | 578 | 1,134 | 2,377 | 2,909 | 3,464 | 4,115 |
| Quebec | 1,407 | 756 | 805 | 578 | 208 | 615 | 1,893 | 2,442 | 3,010 | 3,648 |
| Ontario | 1,987 | 1,322 | 1,344 | 1,134 | 615 | 226 | 1,541 | 2,107 | 2,688 | 3,292 |
| Manitoba | 3,056 | 2,547 | 2,635 | 2,377 | 1,893 | 1,541 | 145 | 604 | 1,173 | 1,780 |
| Saskatchewan | 3,539 | 3,071 | 3,167 | 2,909 | 2,442 | 2,107 | 604 | 234 | 628 | 1,233 |
| Alberta | 4,056 | 3,621 | 3,723 | 3,464 | 3,010 | 2,688 | 1,173 | 628 | 221 | 709 |
| British Columbia | 4,717 | 4,274 | 4,374 | 4,115 | 3,648 | 3,292 | 1,780 | 1,233 | 709 | 213 |
| percent | ||||||||||
| Panel C—Difference between network and great-circle distance | ||||||||||
| Newfoundland and Labrador | 48 | 91 | 61 | 50 | 11 | 40 | 52 | 48 | 50 | 46 |
| Prince Edward Island | 98 | 59 | 72 | 29 | 47 | 29 | 41 | 37 | 33 | 33 |
| Nova Scotia | 74 | 67 | -5 | 34 | 46 | 35 | 37 | 36 | 34 | 33 |
| New Brunswick | 52 | 14 | 37 | 9 | 20 | 20 | 39 | 36 | 32 | 29 |
| Quebec | 5 | 45 | 52 | 26 | 34 | -5 | 30 | 28 | 24 | 26 |
| Ontario | 42 | 31 | 35 | 28 | -3 | -15 | 31 | 33 | 28 | 31 |
| Manitoba | 50 | 38 | 38 | 36 | 27 | 11 | 47 | 8 | 14 | 24 |
| Saskatchewan | 48 | 34 | 36 | 35 | 28 | 28 | 3 | -6 | 9 | 27 |
| Alberta | 43 | 36 | 32 | 32 | 24 | 21 | 12 | 5 | -1 | 28 |
| British Columbia | 46 | 35 | 34 | 33 | 27 | 30 | 26 | 32 | 43 | -5 |
| Source: Statistics Canada, authors' calculations. | ||||||||||
Appendix B Robustness checks
B.1 Testing for the differential effect on distance on intraprovincial and interprovincial trade
If intraprovincial trade is populated with a large set of logistics-truncated flows, the distance parameter on intraprovincial flows should be more negative than that on interprovincial flows, whose pattern results from benchmarking to the flows from the provincial input-output accounts. To test for this effect, a modified version of Equation (5) is estimated,
with the distance parameter permitted to vary across intraprovincial and interprovincial flows using an indicator variable for intraprovincial flows .Note 17 If the truncation effect predominates, the distance parameter on intraprovincial trade should be more negative than that on interprovincial trade. To isolate this effect, the model is estimated with separate origin and destination fixed effects for intraprovincial and interprovincial trade, where indicates the set of intraprovincial regions. Intra-region flows are excluded.Note 18 When estimated for ERs, the distance parameter was -0.769 for interprovincial trade, but significantly less negative for intraprovincial trade (-0.601) . Using CDs, a subunit of ERs, there was no significant difference between the distance parameters on intraprovincial trade . To the extent that it is present, truncation of intraprovincial flows does not appear to be sufficient to bias the estimates.
B.2 Estimates by year
The estimates are presented for trade averaged across the nine-year study period from 2004 through 2012. This is long enough to observe changes stemming from policy initiatives or shifts in the macro-economy. To account for these effects, the baseline model was estimated with all the variables interacted with time-fixed effects, with 2004 being the excluded year. Whether the model is estimated using provinces, ERs, or CDs as the trading units, no significant difference in the coefficients is evident across years (Table B.1). Hence, the average trade level-based estimates reported in the main body of the paper provide a reasonable picture of provincial border effects over the entire period.
| Province | Geography | ||
|---|---|---|---|
| Economic region | Census division | ||
| Own-province | |||
| Coefficient | 0.756Note ** | 0.752Note ** | 0.747Note ** |
| Standard error | 0.113 | 0.128 | 0.093 |
| 2005 | |||
| Coefficient | -0.021 | 0.027 | 0.072 |
| Standard error | 0.149 | 0.194 | 0.150 |
| 2006 | |||
| Coefficient | -0.0449 | 0.0256 | 0.0595 |
| Standard error | 0.143 | 0.180 | 0.134 |
| 2007 | |||
| Coefficient | 0.0548 | 0.1170 | 0.1170 |
| Standard error | 0.144 | 0.189 | 0.128 |
| 2008 | |||
| Coefficient | 0.028 | 0.128 | 0.146 |
| Standard error | 0.151 | 0.187 | 0.145 |
| 2009 | |||
| Coefficient | -0.0173 | -0.0310 | -0.0495 |
| Standard error | 0.158 | 0.173 | 0.131 |
| 2010 | |||
| Coefficient | 0.0663 | 0.1470 | 0.0619 |
| Standard error | 0.180 | 0.196 | 0.134 |
| 2011 | |||
| Coefficient | 0.0192 | -0.0619 | -0.1420 |
| Standard error | 0.174 | 0.190 | 0.132 |
| 2012 | |||
| Coefficient | 0.2630 | -0.0598 | -0.1030 |
| Standard error | 0.248 | 0.171 | 0.127 |
| R-squared | 0.875 | 0.721 | 0.983 |
| Number of observations | 900 | 47,961 | 713,480 |
Source: Statistics Canada, authors' calculations. |
|||
B.3 Differential border effect estimates for Quebec
To test for the effect of Quebec on internal trade, own-province is interacted with an indicator variable for internal Quebec trade flows. While the point estimate on the interaction term is positive, it is not significantly different from zero (Table B.2).
| Distance | Estimates |
|---|---|
| 0 km to 25 km | |
| Coefficient | -0.931Note *** |
| Standard error | 0.122 |
| 25 km to 100 km | |
| Coefficient | -0.273 |
| Standard error | 0.225 |
| 100 km to 500 km | |
| Coefficient | -0.803Note *** |
| Standard error | 0.092 |
| Greater than 500 km | |
| Coefficient | -0.877Note ** |
| Standard error | 0.066 |
| Own-region | |
| Coefficient | 0.176 |
| Standard error | 0.198 |
| Own-province | |
| Coefficient | 0.346Note *** |
| Standard error | 0.0844 |
| Own-province × Quebec | |
| Coefficient | 0.244 |
| Standard error | 0.209 |
| Contiguous regions | |
| Coefficient | -0.139 |
| Standard error | 0.097 |
| Constant | |
| Coefficient | 2.819Note ** |
| Standard error | 0.503 |
| Number of observations | 132,862 |
Source: Statistics Canada, authors' calculations. |
|
References
Agnosteva, D.E., J.E. Anderson, and Y.V. Yotov. 2014. Intra-national Trade Costs: Measurement and Aggregation. NBER Working Paper Series, no. 19872. Cambridge, Massachusetts: National Bureau of Economic Research.
Albrecht, L., and T. Tombe. 2016. “Internal trade, productivity, and interconnected industries: A quantitative analysis.” Canadian Journal of Economics 49 (1).
Amrhein, C.G. 1995. “Searching for the elusive aggregation effect: Evidence from statistical simulation.” Environment and Planning A 27 (1): 105–119.
Amrhein, C.G., and R. Flowerdew. 1992. “The effect of data aggregation on a Poisson regression model of Canadian migration.” Environment and Planning A 24 (10): 1381–1391.
Anderson, J.E. 2010. The Gravity Model. NBER Working Paper Series, no. 16576. Cambridge, Massachusetts: National Bureau of Economic Research.
Anderson, J.E., and E. van Wincoop. 2003. “Gravity with gravitas: A solution to the border puzzle.” American Economic Review 93 (1): 170–192.
Anderson, J.E., and Y.V. Yotov. 2010. “The changing incidence of geography.” American Economic Review 100 (5): 2157–2186.
Anderson, J.E., and Y.V. Yotov. 2012. Gold Standard Gravity. NBER Working Paper Series, no. 17835. Cambridge, Massachusetts: National Bureau of Economic Research.
Arbia, G. 1989. Spatial Data Configuration in Statistical Analysis of Regional Economic and Related Problems. Dordrecht, Netherlands: Kluwer Academic Publishers.
Baldwin, J.R., and W. Gu. 2009. “The impact of trade on plant scale, production-run length and diversification.” In Producer Dynamics: New Evidence from Micro Data, ed. T. Dunne, J.B. Jensen, and M. Roberts. Vol. 68 of Studies in Income and Wealth. National Bureau of Economic Research. Chicago: University of Chicago Press.
Behrens, K., T. Bougna, and W.M. Brown. 2015. The World Is Not Yet Flat: Transportation Costs Matter! CEPR Discussion Paper no. 10356. London: Centre for Economic Policy Research.
Briant, A., P.-P. Combes, and M. Lafourcade. 2010. “Dots to boxes: Do the size and shape of spatial units jeopardize economic geography estimations?” Journal of Urban Economics 67 (3): 287–302.
Brown, W.M. 2003. Overcoming Distance, Overcoming Borders: Comparing North American Regional Trade. Economic Analysis Research Paper Series, no. 8. Statistics Canada Catalogue no. 11F0027M. Ottawa: Statistics Canada.
Brown, W.M. 2015. “How much thicker is the Canada–U.S. border? The cost of crossing the border by truck in the pre- and post-9/11 eras.” Research in Transportation Business and Management 16: 50–56.
Brown, W.M., and W.P. Anderson. 2002. “Spatial markets and the potential for economic integration between Canadian and U.S. regions.” Papers in Regional Science 81 (1): 99–120.
Coughlin, C.C., and D. Novy. 2016. Estimating Border Effects: The Impact of Spatial Aggregation. Federal Reserve Bank of St. Louis Working Paper Series, no. 2016-006A. St. Louis, Missouri: Federal Reserve Bank of St. Louis.
Crafts, N., and A. Klein. 2015. “Geography and intra-national home bias: U.S. domestic trade in 1949 and 2007.” Journal of Economic Geography 15 (3): 477–497.
Fally, T. 2015. “Structural gravity and fixed effects.” Journal of International Economics 97 (1): 76–85.
Fotheringham, A.S., and M.E. O’Kelly. 1989. Spatial Interaction Models: Formulations and Applications. Dordrecht, Netherlands: Kluwer Academic Publishers.
Fotheringham, A.S., and D.W.S. Wong. 1991. “The modifiable areal unit problem in multivariate statistical analysis.” Environment and Planning A 23 (7): 1025–1044.
Généreux, P.A., and B. Langen. The Derivation of Provincial (Inter-regional) Trade Flows: The Canadian Experience. Paper presented at the 14th International Input-Output Techniques Conference, Montréal, October 10 to 15, 2002.
Head, K., and T. Mayer. 2010. “Illusory border effects: Distance mismeasurement inflates estimates of home bias in trade.” In The Gravity Model in International Trade: Advances and Applications, ed. P.A.G. van Bergeijk and S. Brakman, chapter 6, p. 165–192. Cambridge: Cambridge University Press.
Head, K., and T. Mayer. 2013. “What separates us? Sources of resistance to globalization.” Canadian Journal of Economics 46 (4): 1196–1231.
Head, K., and T. Mayer. 2014. “Gravity equations: Workhorse, toolkit, and cookbook.” In Handbook of International Economics, ed. G. Gopinath, E. Helpman, and K. Rogoff, Vol. 4, Chapter 3, p. 131–195. Amsterdam: North Holland.
Hillberry, R., and D. Hummels. 2003. “Intranational home bias: Some explanations.” Review of Economics and Statistics 85 (4): 1089–1092.
Hillberry, R., and D. Hummels. 2008. “Trade responses to geographic frictions: A decomposition using micro-data.” European Economic Review 52 (3): 527–550.
Manning, W., and J. Mullahy. 2001. “Estimating log models: To transform or not to transform?” Journal of Health Economics 20 (4): 461–494.
McCallum, J. 1995. “National borders matter: Canada–U.S. regional trade patterns.” American Economic Review 85 (3): 615–623.
Melitz, M.J., and G.I.P. Ottaviano. 2008. “Market size, trade and productivity.” Review of Economic Studies 75 (1): 295–316.
Millimet, D.L., and T. Osang. 2007. “Do state borders matter for U.S. intranational trade? The role of history and internal migration.” Canadian Journal of Economics 40 (1): 93–126.
Páez, A., and D.M. Scott. 2005. “Spatial statistics for urban analysis: A review of techniques with examples.” GeoJournal 61 (1): 53–67.
Santos Silva, J.M.C., and S. Tenreyro. 2006. “The log of gravity.” Review of Economics and Statistics 88 (4): 641–658.
Sen, A., and T. Smith. 1995. Gravity Models of Spatial Interaction Behavior. Berlin: Springer.
Statistics Canada. n.d.a. Standard Classification of Transported Goods (SCTG) 1996. Last updated on April 17, 2015. Available at: http://www.statcan.gc.ca/eng/subjects/standard/sctg/sctgmenu (accessed January 26, 2017).
Statistics Canada. n.d.b. Standard Geographical Classification (SGC) 2006 - Volume I, The Classification. Last updated January 30, s2017. Archived. Available at: http://www.statcan.gc.ca/eng/subjects/standard/sgc/2006/2006-ind-fin (accessed February 8, 2017).
Wolf, H.C. 2000. “Intranational Home Bias in Trade.” Review of Economics and Statistics 82 (4): 555–563.
The World Bank Group. 2016. Tariff rate, most favored nation, simple mean, all products (%) (Chart, and table giving overview per country). Annual data from 1996 to 2012. Available at: http://data.worldbank.org/indicator/TM.TAX.MRCH.SM.FN.ZS (accessed: January 17, 2017).
- Date modified:
