Les nouveautés en matière de comptes économiques canadiens
Ajustement saisonnier des flux et des stocks dans les comptes financiers et du patrimoine : vers une approche intégrée
 Consulter la version la plus récente.
Consulter la version la plus récente.
Information archivée dans le Web
L’information dont il est indiqué qu’elle est archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Elle n’est pas assujettie aux normes Web du gouvernement du Canada et elle n’a pas été modifiée ou mise à jour depuis son archivage. Pour obtenir cette information dans un autre format, veuillez communiquer avec nous.
Passer au texte
Début du texte
Avis de correction
L’annexe a été mise-a-jour pour inclure une correction dans la formule pour calculer d’ACA désaisonnalisée.
Introduction
Les comptes financiers et du patrimoine (CFP) décrivent avec précision le patrimoine financier et non financier du Canada. Les comptes financiers et du patrimoine se composent du compte du bilan national (CBN), qui mesure les stocks d’actifs et de passifs financiers; du compte des flux financiers (CFF), qui mesure les opérations nettes des actifs et des passifs financiers portant sur les mêmes instruments, et du compte des autres changements d’actifs (ACA), qui mesure la réévaluation des stocks existants afin de tenir compte des variations des prix et d’autres changements de volume. Autrement dit, ces comptes forment une ventilation des flux financiers qui font croître et diminuer la richesse d’un secteur institutionnel, c’est-à-dire la valeur marchande des actifs et des passifs à un moment donné. Ces comptes sont produits sur une base trimestrielle.
Dans les CFP, il y a un lien direct entre les stocks de fermeture de la période précédente et de la période en cours avec l’accumulation des flux financiers, (c’est-à-dire les opérations financières nettes, les réévaluations attribuables aux effets des prix et les autres changements de volume), comptant pour la différence (voir l’encadré 1). De plus, cette identité stock-flux doit être maintenue tout au long de la série chronologique de sorte que les trois comptes soient uniformes et cohérents. Pour de plus amples renseignements sur les comptes financiers et du patrimoine, veuillez consulter le chapitre 7 du Guide de l’utilisateur : Système de comptabilité nationale du Canada.
Début de la boîte de texteoù,
= position du stock de l’instrument au moment t dans le CBN
= position du stock de l’instrument au moment t-1 dans le CBN
= flux des opérations nettes de l’instrument au moment t dans le CFF
= autres changements dans les actifs de l’instrument pour la période t dans le ACA
La principale raison de produire des estimations des emprunts du secteur des ménages désaisonnalisés résulte de l’observation de changements saisonniers dans les estimations de la dette sur le marché du crédit non désaisonnalisées. Par exemple, les Canadiens ont tendance à emprunter davantage sous forme de crédit à la consommation au quatrième trimestre, avec l’arrivée d’une importante activité de vente au détail liée à la période des Fêtes, puis à emprunter moins au premier trimestre. De plus, les emprunts hypothécaires ont tendance à ralentir au premier trimestre, puis à reprendre aux deuxièmes et troisièmes trimestres, à mesure que l’hiver se retire dans de nombreuses régions du Canada, période où l’activité de revente augmente et où les familles cherchent un logement sûr avant le début de la nouvelle année scolaire. Ces tendances cycliques infra-annuelles ne se limitent pas au secteur des ménages et peuvent être observées dans d’autres secteurs, comme les emprunts de l’État. Dans ce contexte, l’ajustement saisonnier des données améliore l’interprétation des estimations des composantes qui présentent des tendances cycliques prononcées en éliminant la variation attribuable aux événements prévisibles et récurrents. De cette façon, il est possible de fournir aux utilisateurs de données, aux chercheurs et aux décideurs politiques des données plus exactes sur les mouvements d’un trimestre à l’autre reflétant les tendances sous-jacentes de ces mouvements. Bien que le domaine d’intérêt actuel soit les emprunts des ménages, cette méthode sera ultérieurement mise en place pour d’autres secteurs pertinents des comptes financiers et du patrimoine. Cependant, l’intention n’est pas de désaisonnaliser tous les instruments et secteurs de l’économie.
Les estimations désaisonnalisées des emprunts actuellement disponibles dans le CFP sont axées sur les opérations financières des ménages. Par conséquent, la saisonnalité contenue dans les stocks de la dette des ménages n’est pas prise en compte, puisque les stocks de fin de période sont une accumulation des opérations financières non ajustées. Afin de mettre en place un cadre cohérent pour les comptes financiers et du patrimoine, il est recommandé d’adopter une approche intégrée de d’ajustement saisonnier des flux et des stocks. En effet, l’identité stocks-flux doit être maintenue, que les données soient désaisonnalisées ou non, et le fait d’avoir en place un cadre unifié pour ces données facilite le maintien de cette identité.
L’une des conséquences de l’absence d’estimations des stocks désaisonnalisées est que le ratio de la dette sur le marché du crédit des ménages au revenu disponible présente une saisonnalité résultant de sa composante non ajustée de la saisonnalité (voir le graphique 1). Compte tenu de cette présence saisonnière, il est courant pour les utilisateurs d’interpréter certains trimestres comme ayant atteints des records élevés du ratio, alors que ces données illustrent simplement une tendance cyclique prévisible. Les utilisateurs surveillent de près ce ratio, puisqu’il s’agit de l’un des nombreux indicateurs de la vulnérabilité du secteur des ménages, ce qui souligne l’importance d’évaluer avec précision les tendances trimestrielles de l’endettement des ménages.

Tableau de données du graphique 1
| Ratio de la dette sur le marché du crédit au revenu disponible, données non désaisonnalisées | |
|---|---|
| pourcentage | |
| 2010 | |
| Première trimestre | 155,2 |
| Deuxième trimestre | 156,9 |
| Troisième trimestre | 158,0 |
| Quatrième trimestre | 158,3 |
| 2011 | |
| Première trimestre | 157,2 |
| Deuxième trimestre | 158,4 |
| Troisième trimestre | 159,1 |
| Quatrième trimestre | 159,5 |
| 2012 | |
| Première trimestre | 158,5 |
| Deuxième trimestre | 159,8 |
| Troisième trimestre | 160,4 |
| Quatrième trimestre | 160,2 |
| 2013 | |
| Première trimestre | 159,7 |
| Deuxième trimestre | 160,5 |
| Troisième trimestre | 161,1 |
| Quatrième trimestre | 160,7 |
| 2014 | |
| Première trimestre | 160,2 |
| Deuxième trimestre | 161,2 |
| Troisième trimestre | 162,4 |
| Quatrième trimestre | 162,4 |
| 2015 | |
| Première trimestre | 161,5 |
| Deuxième trimestre | 162,9 |
| Troisième trimestre | 164,1 |
| Quatrième trimestre | 164,8 |
| 2016 | |
| Première trimestre | 166,5 |
| Deuxième trimestre | 170,1 |
| Troisième trimestre | 172,2 |
| Quatrième trimestre | 173,3 |
| 2017 | |
| Première trimestre | 172,7 |
| Deuxième trimestre | 174,1 |
| Troisième trimestre | 174,3 |
| Quatrième trimestre | 173,8 |
| 2018 | |
| Première trimestre | 172,3 |
| Deuxième trimestre | 173,2 |
| Troisième trimestre | 173,8 |
| Source : Statistique Canada, « Désaisonnalisation des stocks et des flux des comptes financiers et du patrimoine : vers une méthode intégrée », Les nouveautés en matière de comptes économiques canadiens (13-605-X), 2018. | |
L’ajustement saisonnier est une technique qui vise à déceler, à estimer et à éliminer les variations saisonnières dans une série chronologique. Ces variations sont attribuables à des facteurs institutionnels et climatiques et l’on s’attend à ce qu’elles se reproduisent aux mêmes moments avec une intensité semblable. Les séries chronologiques désaisonnalisées ne comprennent que le cycle de tendance et les composantes irrégulières. Cela donne une idée approximative des changements sous-jacents dans les tendances et facilite l’analyse de la dynamique à court terme.
Pour obtenir plus de renseignements sur l’ajustement saisonnier, voir le document intitulé Données désaisonnalisées – Foire aux questions.
Pour ces raisons, Statistique Canada a lancé un projet visant à étudier différentes méthodes pour produire un ensemble intégré de données sur les flux financiers, les stocks et les autres changements d’actifs désaisonnalisées qui pourraient être utilisées de façon générale dans les CFP, et de façon plus précise pour produire un ensemble d’estimations cohérentes de la dette des ménages sur le marché du crédit. Ce dernier pourrait à son tour être utilisé pour établir des indicateurs financiers utiles.
Méthode de d’ajustement saisonnier des flux et des stocks
En général, les séries chronologiques peuvent être classées en deux catégories : les stocks et les flux. Une série de stocks est une mesure de l’ampleur des attributs à un moment précis dans le temps, tandis qu’une série de flux renvoie à la valeur accumulée sur une période donnée. Dans les CFP, le CBN enregistre les stocks ou la valeur des actifs et des passifs à la fin du trimestre, tandis que le CFF et l
Statistique Canada a étudié une multitude de méthodes qui produiraient les résultats souhaités. Après avoir testé différents modèles et hypothèses et mené des auprès d’experts et d’utilisateurs, Statistique Canada a déterminé que la méthode la plus pratique et la plus valide sur le plan conceptuel était la suivante : 1) désaisonnaliser de façon directe une version du stock obtenue en utilisant les flux et ACA non désaisonnalisés, 2) désaisonnaliser de façon directe les stocks du CBN non désaisonnalisés après soustraction du ACA non désaisonnalisés et 3) dériver de façon indirecte des flux du CFF désaisonnalisés à partir des stocks du CBN. Les étapes précises sont détaillées dans l’annexe.
Cette méthode a été adoptée pour chaque composante de la dette des ménages sur le marché du crédit, y compris les prêts hypothécaires, les prêts non hypothécaires et le crédit à la consommation. Les séries désaisonnalisées ainsi obtenues ont ensuite été agrégées pour produire une estimation de la dette totale des ménages sur le marché du crédit.
Résultats
Quelques résultats obtenus de la méthode intégrée de désaisonnalisation des flux et des stocks des CFP sont présentés ci-dessous. Ces données sont accessibles dans le tableau de données 38-10-0238.
Endettement des ménages sur le marché du crédit, flux désaisonnalisés
Le graphique 2 montre que les flux financiers désaisonnalisés de la dette totale sur le marché du crédit et les estimations non désaisonnalisées se recoupent, préservant le niveau d’estimés moyens sur une base temporelle. La série non désaisonnalisée indique d’importantes baisses au cours du premier trimestre de chaque année, suivies d’un sommet aux deuxième et troisième trimestres. À titre comparatif, au premier trimestre de 2018, les flux désaisonnalisés ont diminué de 4,2 milliards de dollars, tandis que les estimations non désaisonnalisées ont diminué de 15,9 milliards de dollars.
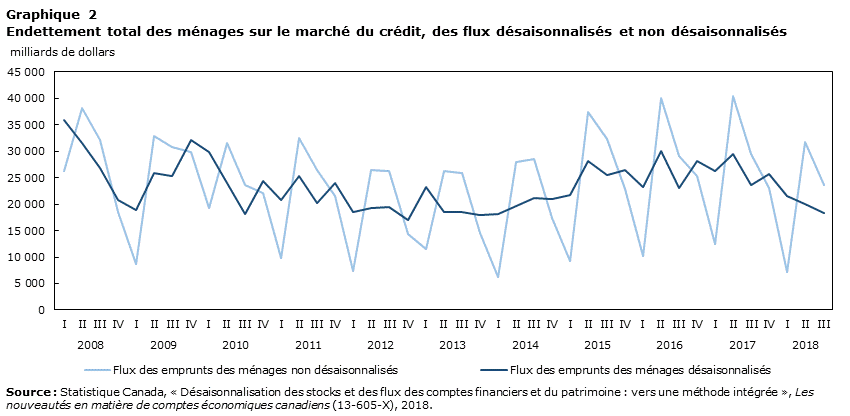
Tableau de données du graphique 2
| Flux des emprunts des ménages non désaisonnalisés | Flux des emprunts des ménages désaisonnalisés | |
|---|---|---|
| milliards de dollars | ||
| 2008 | ||
| Première trimestre | 26 247 | 35 967 |
| Deuxième trimestre | 38 218 | 31 448 |
| Troisième trimestre | 32 067 | 26 844 |
| Quatrième trimestre | 18 491 | 20 684 |
| 2009 | ||
| Première trimestre | 8 746 | 18 887 |
| Deuxième trimestre | 32 886 | 25 814 |
| Troisième trimestre | 30 715 | 25 212 |
| Quatrième trimestre | 29 898 | 32 158 |
| 2010 | ||
| Première trimestre | 19 182 | 29 905 |
| Deuxième trimestre | 31 505 | 24 008 |
| Troisième trimestre | 23 688 | 18 079 |
| Quatrième trimestre | 22 167 | 24 430 |
| 2011 | ||
| Première trimestre | 9 771 | 20 697 |
| Deuxième trimestre | 32 541 | 25 233 |
| Troisième trimestre | 26 351 | 20 173 |
| Quatrième trimestre | 21 442 | 23 898 |
| 2012 | ||
| Première trimestre | 7 298 | 18 498 |
| Deuxième trimestre | 26 468 | 19 189 |
| Troisième trimestre | 26 291 | 19 529 |
| Quatrième trimestre | 14 277 | 17 075 |
| 2013 | ||
| Première trimestre | 11 577 | 23 206 |
| Deuxième trimestre | 26 166 | 18 582 |
| Troisième trimestre | 25 930 | 18 568 |
| Quatrième trimestre | 14 545 | 17 984 |
| 2014 | ||
| Première trimestre | 6 245 | 18 209 |
| Deuxième trimestre | 28 020 | 19 720 |
| Troisième trimestre | 28 435 | 21 137 |
| Quatrième trimestre | 17 346 | 20 929 |
| 2015 | ||
| Première trimestre | 9 217 | 21 774 |
| Deuxième trimestre | 37 351 | 28 110 |
| Troisième trimestre | 32 343 | 25 446 |
| Quatrième trimestre | 22 830 | 26 376 |
| 2016 | ||
| Première trimestre | 10 236 | 23 202 |
| Deuxième trimestre | 40 118 | 30 025 |
| Troisième trimestre | 29 114 | 22 948 |
| Quatrième trimestre | 25 217 | 28 215 |
| 2017 | ||
| Première trimestre | 12 376 | 26 187 |
| Deuxième trimestre | 40 443 | 29 409 |
| Troisième trimestre | 29 384 | 23 690 |
| Quatrième trimestre | 22 988 | 25 718 |
| 2018 | ||
| Première trimestre | 7 115 | 21 489 |
| Deuxième trimestre | 31 684 | 20 014 |
| Troisième trimestre | 23 668 | 18 272 |
| Source : Statistique Canada, « Désaisonnalisation des stocks et des flux des comptes financiers et du patrimoine : vers une méthode intégrée », Les nouveautés en matière de comptes économiques canadiens (13-605-X), 2018. | ||
Niveaux d’endettement total des ménages sur le marché du crédit, données désaisonnalisées
Comme pour les flux financiers, le taux de croissance des stocks non désaisonnalisés de la dette des ménages affiche une tendance saisonnière semblable au taux de croissance de la série désaisonnalisée, les deux courbes se recoupant encore une fois. À titre de comparaison, le taux de croissance d’une année à l’autre affiche aussi une tendance long terme semblable, mais ne fournit pas une indication aussi fiable des mouvements d’un trimestre à l’autre.

Tableau de données du graphique 3
| Niveau d'endettement non désaisonnalisé d’un trimestre à l’autre (axe de gauche) | Niveau d'endettement désaisonnalisé d’un trimestre à l’autre (axe de gauche) | Niveau d'endettement non désaisonnalisé d’une année à l’autre (axe de droite) | |
|---|---|---|---|
| pourcentage | |||
| 2000 | |||
| Première trimestre | 1,6 | 2,2 | 7,4 |
| Deuxième trimestre | 1,7 | 1,4 | 7,1 |
| Troisième trimestre | 2,0 | 1,6 | 7,2 |
| Quatrième trimestre | 1,2 | 1,3 | 6,6 |
| 2001 | |||
| Première trimestre | 0,4 | 1,1 | 5,4 |
| Deuxième trimestre | 1,7 | 1,3 | 5,5 |
| Troisième trimestre | 1,9 | 1,5 | 5,4 |
| Quatrième trimestre | 1,5 | 1,5 | 5,7 |
| 2002 | |||
| Première trimestre | 1,5 | 2,3 | 6,8 |
| Deuxième trimestre | 2,6 | 2,1 | 7,7 |
| Troisième trimestre | 2,3 | 1,9 | 8,1 |
| Quatrième trimestre | 1,8 | 1,8 | 8,4 |
| 2003 | |||
| Première trimestre | 0,8 | 1,8 | 7,7 |
| Deuxième trimestre | 2,2 | 1,5 | 7,2 |
| Troisième trimestre | 2,8 | 2,5 | 7,8 |
| Quatrième trimestre | 2,4 | 2,4 | 8,4 |
| 2004 | |||
| Première trimestre | 1,4 | 2,4 | 9,1 |
| Deuxième trimestre | 3,9 | 3,3 | 11,0 |
| Troisième trimestre | 2,7 | 2,3 | 10,8 |
| Quatrième trimestre | 2,6 | 2,7 | 11,1 |
| 2005 | |||
| Première trimestre | 2,3 | 3,2 | 12,1 |
| Deuxième trimestre | 3,0 | 2,4 | 11,1 |
| Troisième trimestre | 2,9 | 2,5 | 11,3 |
| Quatrième trimestre | 2,3 | 2,4 | 10,9 |
| 2006 | |||
| Première trimestre | 1,9 | 2,8 | 10,5 |
| Deuxième trimestre | 2,8 | 2,2 | 10,2 |
| Troisième trimestre | 2,9 | 2,5 | 10,2 |
| Quatrième trimestre | 2,8 | 2,9 | 10,8 |
| 2007 | |||
| Première trimestre | 2,0 | 2,9 | 10,9 |
| Deuxième trimestre | 3,6 | 3,0 | 11,8 |
| Troisième trimestre | 3,3 | 2,9 | 12,2 |
| Quatrième trimestre | 2,4 | 2,5 | 11,8 |
| 2008 | |||
| Première trimestre | 2,1 | 2,9 | 11,9 |
| Deuxième trimestre | 3,0 | 2,5 | 11,2 |
| Troisième trimestre | 2,5 | 2,0 | 10,3 |
| Quatrième trimestre | 1,4 | 1,5 | 9,2 |
| 2009 | |||
| Première trimestre | 0,6 | 1,4 | 7,7 |
| Deuxième trimestre | 2,4 | 1,8 | 7,0 |
| Troisième trimestre | 2,1 | 1,7 | 6,7 |
| Quatrième trimestre | 2,1 | 2,2 | 7,4 |
| 2010 | |||
| Première trimestre | 0,8 | 1,5 | 7,5 |
| Deuxième trimestre | 2,1 | 1,6 | 7,3 |
| Troisième trimestre | 1,5 | 1,2 | 6,6 |
| Quatrième trimestre | 1,4 | 1,6 | 6,0 |
| 2011 | |||
| Première trimestre | 0,1 | 0,8 | 5,2 |
| Deuxième trimestre | 2,1 | 1,6 | 5,2 |
| Troisième trimestre | 1,7 | 1,3 | 5,3 |
| Quatrième trimestre | 1,3 | 1,5 | 5,2 |
| 2012 | |||
| Première trimestre | 0,3 | 1,0 | 5,4 |
| Deuxième trimestre | 1,6 | 1,1 | 4,9 |
| Troisième trimestre | 1,6 | 1,1 | 4,8 |
| Quatrième trimestre | 0,8 | 1,0 | 4,3 |
| 2013 | |||
| Première trimestre | 0,6 | 1,3 | 4,6 |
| Deuxième trimestre | 1,5 | 1,1 | 4,5 |
| Troisième trimestre | 1,5 | 1,0 | 4,5 |
| Quatrième trimestre | 0,8 | 1,0 | 4,4 |
| 2014 | |||
| Première trimestre | 0,3 | 1,0 | 4,2 |
| Deuxième trimestre | 1,5 | 1,1 | 4,2 |
| Troisième trimestre | 1,6 | 1,2 | 4,3 |
| Quatrième trimestre | 0,9 | 1,1 | 4,4 |
| 2015 | |||
| Première trimestre | 0,6 | 1,3 | 4,7 |
| Deuxième trimestre | 2,0 | 1,5 | 5,1 |
| Troisième trimestre | 1,7 | 1,3 | 5,3 |
| Quatrième trimestre | 1,2 | 1,4 | 5,5 |
| 2016 | |||
| Première trimestre | 0,7 | 1,4 | 5,7 |
| Deuxième trimestre | 2,0 | 1,5 | 5,7 |
| Troisième trimestre | 1,4 | 1,1 | 5,4 |
| Quatrième trimestre | 1,2 | 1,4 | 5,4 |
| 2017 | |||
| Première trimestre | 0,6 | 1,2 | 5,3 |
| Deuxième trimestre | 1,9 | 1,4 | 5,2 |
| Troisième trimestre | 1,4 | 1,1 | 5,2 |
| Quatrième trimestre | 1,0 | 1,2 | 5,0 |
| 2018 | |||
| Première trimestre | 0,3 | 1,0 | 4,7 |
| Deuxième trimestre | 1,4 | 0,9 | 4,2 |
| Troisième trimestre | 1,0 | 0,8 | 3,9 |
| Source : Statistique Canada, « Désaisonnalisation des stocks et des flux des comptes financiers et du patrimoine : vers une méthode intégrée », Les nouveautés en matière de comptes économiques canadiens (13-605-X), 2018. | |||
Dette sur le marché du crédit en proportion du revenu disponible, données désaisonnalisées
Jusqu’à présent, la mesure canadienne de la dette sur le marché du crédit en proportion du revenu disponible a été calculée comme la dette totale des ménages sur le marché du crédit divisée par une somme cumulative sur quatre trimestres du revenu disponible des ménages (RDM). Cette méthode a été utilisée afin de réduire la saisonnalité présente dans le RDM non désaisonnalisé et placer le revenu sur la même base que la dette (c’est-à-dire une estimation annuelle du revenu équivalente au stock de fin d’année).
Début de la boîte de texteAu Canada, la dette totale sur le marché du crédit pour le secteur des ménages est définie comme la somme du crédit à la consommation, de la dette hypothécaire et de la dette non hypothécaire. Un indicateur utile de la santé financière des ménages est le ratio entre cette dette et le revenu disponible annuel des ménages.
Le graphique 4 illustre le ratio de la dette sur le marché du crédit au revenu disponible en utilisant des données désaisonnalisées. Ce ratio comprend deux principaux changements : 1) le niveau d’endettement désaisonnalisé comme numérateur et 2) le revenu disponible des ménages désaisonnalisé aux taux annuels.

Tableau de données du graphique 4
| Ratio de la dette sur le marché du crédit au revenu disponible en données non désaisonnalisées publié (axe de gauche) | Ratio de la dette sur le marché du crédit au revenu disponible en données désaisonnalisées (axe de gauche) | Révisions (axe de droite) | |
|---|---|---|---|
| pourcentage | |||
| 2000 | |||
| Première trimestre | 105,6 | 110,4 | 4,7 |
| Deuxième trimestre | 105,7 | 110,1 | 4,3 |
| Troisième trimestre | 106,0 | 109,4 | 3,4 |
| Quatrième trimestre | 105,3 | 109,0 | 3,6 |
| 2001 | |||
| Première trimestre | 104,0 | 106,8 | 2,8 |
| Deuxième trimestre | 104,9 | 110,4 | 5,5 |
| Troisième trimestre | 105,8 | 109,1 | 3,3 |
| Quatrième trimestre | 106,6 | 109,8 | 3,2 |
| 2002 | |||
| Première trimestre | 107,4 | 110,6 | 3,2 |
| Deuxième trimestre | 108,8 | 112,6 | 3,8 |
| Troisième trimestre | 110,1 | 112,8 | 2,7 |
| Quatrième trimestre | 110,9 | 113,8 | 2,9 |
| 2003 | |||
| Première trimestre | 111,0 | 114,1 | 3,1 |
| Deuxième trimestre | 112,0 | 116,5 | 4,5 |
| Troisième trimestre | 114,2 | 119,0 | 4,7 |
| Quatrième trimestre | 116,2 | 120,4 | 4,3 |
| 2004 | |||
| Première trimestre | 116,9 | 121,7 | 4,8 |
| Deuxième trimestre | 120,1 | 122,7 | 2,6 |
| Troisième trimestre | 121,6 | 124,1 | 2,6 |
| Quatrième trimestre | 122,9 | 126,8 | 3,9 |
| 2005 | |||
| Première trimestre | 124,5 | 131,4 | 6,9 |
| Deuxième trimestre | 127,0 | 131,5 | 4,5 |
| Troisième trimestre | 129,2 | 133,9 | 4,7 |
| Quatrième trimestre | 130,5 | 134,7 | 4,2 |
| 2006 | |||
| Première trimestre | 130,4 | 134,3 | 4,0 |
| Deuxième trimestre | 132,2 | 137,1 | 4,9 |
| Troisième trimestre | 134,0 | 136,8 | 2,8 |
| Quatrième trimestre | 135,4 | 138,2 | 2,8 |
| 2007 | |||
| Première trimestre | 136,6 | 139,2 | 2,6 |
| Deuxième trimestre | 139,6 | 143,8 | 4,2 |
| Troisième trimestre | 142,0 | 147,2 | 5,2 |
| Quatrième trimestre | 143,2 | 148,4 | 5,2 |
| 2008 | |||
| Première trimestre | 145,0 | 149,9 | 4,9 |
| Deuxième trimestre | 147,2 | 151,0 | 3,8 |
| Troisième trimestre | 147,9 | 151,1 | 3,2 |
| Quatrième trimestre | 148,1 | 153,7 | 5,6 |
| 2009 | |||
| Première trimestre | 148,4 | 156,5 | 8,0 |
| Deuxième trimestre | 151,4 | 158,5 | 7,1 |
| Troisième trimestre | 154,3 | 158,2 | 3,9 |
| Quatrième trimestre | 156,5 | 159,4 | 3,0 |
| 2010 | |||
| Première trimestre | 155,2 | 158,1 | 2,9 |
| Deuxième trimestre | 156,9 | 162,6 | 5,8 |
| Troisième trimestre | 158,0 | 162,0 | 4,0 |
| Quatrième trimestre | 158,3 | 161,6 | 3,2 |
| 2011 | |||
| Première trimestre | 157,2 | 162,0 | 4,8 |
| Deuxième trimestre | 158,4 | 164,0 | 5,6 |
| Troisième trimestre | 159,1 | 164,5 | 5,3 |
| Quatrième trimestre | 159,5 | 163,7 | 4,2 |
| 2012 | |||
| Première trimestre | 158,5 | 164,0 | 5,5 |
| Deuxième trimestre | 159,8 | 165,1 | 5,4 |
| Troisième trimestre | 160,4 | 164,9 | 4,5 |
| Quatrième trimestre | 160,2 | 165,3 | 5,1 |
| 2013 | |||
| Première trimestre | 159,7 | 163,9 | 4,2 |
| Deuxième trimestre | 160,5 | 164,7 | 4,2 |
| Troisième trimestre | 161,1 | 165,4 | 4,4 |
| Quatrième trimestre | 160,7 | 165,2 | 4,5 |
| 2014 | |||
| Première trimestre | 160,2 | 165,7 | 5,5 |
| Deuxième trimestre | 161,2 | 166,6 | 5,4 |
| Troisième trimestre | 162,4 | 165,8 | 3,4 |
| Quatrième trimestre | 162,4 | 167,1 | 4,7 |
| 2015 | |||
| Première trimestre | 161,5 | 164,8 | 3,4 |
| Deuxième trimestre | 162,9 | 166,4 | 3,5 |
| Troisième trimestre | 164,1 | 167,8 | 3,7 |
| Quatrième trimestre | 164,8 | 170,5 | 5,7 |
| 2016 | |||
| Première trimestre | 166,5 | 175,6 | 9,0 |
| Deuxième trimestre | 170,1 | 176,4 | 6,3 |
| Troisième trimestre | 172,2 | 176,1 | 3,9 |
| Quatrième trimestre | 173,3 | 176,7 | 3,4 |
| 2017 | |||
| Première trimestre | 172,7 | 178,2 | 5,5 |
| Deuxième trimestre | 174,1 | 177,8 | 3,7 |
| Troisième trimestre | 174,3 | 176,5 | 2,1 |
| Quatrième trimestre | 173,8 | 176,3 | 2,5 |
| 2018 | |||
| Première trimestre | 172,3 | 177,8 | 5,5 |
| Deuxième trimestre | 173,2 | 177,4 | 4,3 |
| Troisième trimestre | 173,8 | 177,5 | 3,7 |
| Source : Statistique Canada, « Désaisonnalisation des stocks et des flux des comptes financiers et du patrimoine : vers une méthode intégrée », Les nouveautés en matière de comptes économiques canadiens (13-605-X), 2018. | |||
Plusieurs raisons justifient l’utilisation de l’estimation du RDM des ménages en données désaisonnalisées aux taux annuels (RDM DTA). Tout d’abord, il s’agit déjà d’une estimation clé publiée dans les comptes des revenus et dépenses, dans lesquels les séries désaisonnalisées sont utilisées pour analyser les mouvements trimestriels. De plus, le RDM DTA permet d’illustrer les changements importants plus rapidement, ce qui en fait une meilleure option pour l’évaluation de la vulnérabilité financière changeante des ménages.
Une mise en garde évidente concernant l’utilisation du RDM DTA est que le ratio sera plus volatile comparativement à la simple utilisation d’une somme mobile. Cependant, l’utilisation du RDM DTA permet de dresser un portrait plus fidèle des tendances d’un trimestre à l’autre du RDM et de tenir compte du poids total de chaque trimestre dans le ratio, plutôt qu’une moyenne de plusieurs trimestres.
Si nous décomposons les révisions du ratio dues à l’introduction d’une dette des ménages corrigée des variations saisonnières à l’incorporation d’un nouveau dénominateur du RDM (voir graphique 5), les résultats sont évidents. Premièrement, les révisions résultant de l’utilisation de la dette corrigée des variations saisonnières reflètent la suppression de la saisonnalité du ratio et leur variabilité est assez minime. Deuxièmement, avec l’introduction de la RDM DTA, il est clair que les révisions sont relativement plus importantes et variables. Une conclusion importante est que même si le ratio est corrigé des variations saisonnières, il reste soumis à de fortes fluctuations et à une volatilité non imputable à des facteurs saisonniers, mais plutôt à des fluctuations du niveau de revenu désaisonnalisé.

Tableau de données du graphique 5
| Révisions dues à l'incorporation des données désaisonnalisées de l’endettement des ménages | Révisions dues à l'incorporation des données désaisonnalisées du revenu personnel disponible | |
|---|---|---|
| pourcentage | ||
| 2000 | ||
| Première trimestre | 0,4 | 4,4 |
| Deuxième trimestre | 0,1 | 4,2 |
| Troisième trimestre | -0,3 | 3,7 |
| Quatrième trimestre | -0,3 | 3,9 |
| 2001 | ||
| Première trimestre | 0,5 | 2,3 |
| Deuxième trimestre | 0,1 | 5,4 |
| Troisième trimestre | -0,3 | 3,6 |
| Quatrième trimestre | -0,3 | 3,5 |
| 2002 | ||
| Première trimestre | 0,6 | 2,6 |
| Deuxième trimestre | 0,0 | 3,8 |
| Troisième trimestre | -0,4 | 3,0 |
| Quatrième trimestre | -0,3 | 3,3 |
| 2003 | ||
| Première trimestre | 0,7 | 2,4 |
| Deuxième trimestre | 0,0 | 4,5 |
| Troisième trimestre | -0,4 | 5,1 |
| Quatrième trimestre | -0,4 | 4,6 |
| 2004 | ||
| Première trimestre | 0,8 | 4,0 |
| Deuxième trimestre | 0,0 | 2,6 |
| Troisième trimestre | -0,4 | 3,0 |
| Quatrième trimestre | -0,4 | 4,3 |
| 2005 | ||
| Première trimestre | 0,8 | 6,1 |
| Deuxième trimestre | 0,0 | 4,5 |
| Troisième trimestre | -0,5 | 5,2 |
| Quatrième trimestre | -0,3 | 4,5 |
| 2006 | ||
| Première trimestre | 0,8 | 3,2 |
| Deuxième trimestre | 0,0 | 4,9 |
| Troisième trimestre | -0,5 | 3,3 |
| Quatrième trimestre | -0,3 | 3,1 |
| 2007 | ||
| Première trimestre | 0,8 | 1,8 |
| Deuxième trimestre | 0,0 | 4,2 |
| Troisième trimestre | -0,5 | 5,7 |
| Quatrième trimestre | -0,3 | 5,5 |
| 2008 | ||
| Première trimestre | 0,8 | 4,1 |
| Deuxième trimestre | 0,0 | 3,8 |
| Troisième trimestre | -0,5 | 3,8 |
| Quatrième trimestre | -0,3 | 5,9 |
| 2009 | ||
| Première trimestre | 0,8 | 7,2 |
| Deuxième trimestre | 0,0 | 7,1 |
| Troisième trimestre | -0,6 | 4,5 |
| Quatrième trimestre | -0,3 | 3,3 |
| 2010 | ||
| Première trimestre | 0,8 | 2,1 |
| Deuxième trimestre | 0,0 | 5,7 |
| Troisième trimestre | -0,6 | 4,6 |
| Quatrième trimestre | -0,3 | 3,5 |
| 2011 | ||
| Première trimestre | 0,8 | 4,0 |
| Deuxième trimestre | 0,1 | 5,5 |
| Troisième trimestre | -0,6 | 5,9 |
| Quatrième trimestre | -0,3 | 4,5 |
| 2012 | ||
| Première trimestre | 0,8 | 4,7 |
| Deuxième trimestre | 0,1 | 5,3 |
| Troisième trimestre | -0,6 | 5,0 |
| Quatrième trimestre | -0,3 | 5,4 |
| 2013 | ||
| Première trimestre | 0,8 | 3,4 |
| Deuxième trimestre | 0,1 | 4,1 |
| Troisième trimestre | -0,6 | 5,0 |
| Quatrième trimestre | -0,3 | 4,7 |
| 2014 | ||
| Première trimestre | 0,8 | 4,7 |
| Deuxième trimestre | 0,1 | 5,4 |
| Troisième trimestre | -0,6 | 4,0 |
| Quatrième trimestre | -0,3 | 5,0 |
| 2015 | ||
| Première trimestre | 0,8 | 2,5 |
| Deuxième trimestre | 0,0 | 3,5 |
| Troisième trimestre | -0,6 | 4,3 |
| Quatrième trimestre | -0,3 | 6,0 |
| 2016 | ||
| Première trimestre | 0,8 | 8,2 |
| Deuxième trimestre | 0,0 | 6,3 |
| Troisième trimestre | -0,6 | 4,5 |
| Quatrième trimestre | -0,3 | 3,7 |
| 2017 | ||
| Première trimestre | 0,9 | 4,6 |
| Deuxième trimestre | -0,1 | 3,7 |
| Troisième trimestre | -0,5 | 2,6 |
| Quatrième trimestre | -0,3 | 2,8 |
| 2018 | ||
| Première trimestre | 0,9 | 4,6 |
| Deuxième trimestre | -0,1 | 4,3 |
| Troisième trimestre | -0,5 | 4,2 |
| Source : Statistique Canada, « Désaisonnalisation des stocks et des flux des comptes financiers et du patrimoine : vers une méthode intégrée », Les nouveautés en matière de comptes économiques canadiens (13-605-X), 2018. | ||
Conclusion
Le présent document avait pour objectif de documenter le processus de détermination d’une méthode appropriée pour l’ajustement saisonnier intégré des flux et des stocks dans les comptes financiers et du patrimoine, et de présenter un aperçu des résultats de cette méthode. Cette méthode devrait être appliquée à l’ensemble des comptes financiers et du patrimoine afin d’améliorer l’interprétation et la pertinence d’autres séries de données contenant de la saisonnalité.
Annexe : Renseignements supplémentaires sur la méthode d’ajustement saisonnier des flux et des stocks
Statistique Canada utilise la méthodologie X-12 ARIMA pour produire des données désaisonnalisées. Les séries chronologiques sont analysées chaque année, et les spécifications optimales sont sélectionnées. Il peut arriver qu’une série chronologique ne présente aucune preuve de saisonnalité. Dans ces cas, les données désaisonnalisées et non désaisonnalisées forment une seule et même série. L’ajustement saisonnier des comptes financiers et du patrimoine est effectuée en temps réel, en ce sens que l’ajustement saisonnier incorpore les renseignements les plus récents pour la période en question, contrairement à l’utilisation de facteurs saisonniers fixes qui ne sont mis à jour que périodiquement.
Dans les cas où des séries détaillées sont regroupées en une série agrégée (agrégat), par exemple des séries sur les types d’emprunts granulaires formant une série sur le total des emprunts, il existe deux méthodes principales. La première consiste à désaisonnaliser les séries détaillées et à les regrouper en une série agrégée, puis à les vérifier pour détecter toute saisonnalité résiduelle. La deuxième consiste à désaisonnaliser à la fois les séries détaillées et la série agrégée et à utiliser une méthode de réconciliation pour s’assurer que l’additivité est respectée. Par souci de simplicité, on utilise la première méthode et on vérifie régulièrement toutes les estimations résultantes de manière à s’assurer qu’elles sont exemptes de saisonnalité résiduelle.
Une autre contrainte facultative du modèle X-12 ARIMA consiste à forcer le total des flux annuels à être égaux dans les séries désaisonnalisées et non désaisonnalisés. Cela vise à faire en sorte que l’accumulation des flux au cours d’une année civile sera identique et utile dans les cas où il existe des points de repère annuels pour certaines séries de flux, comme le produit intérieur brut. Une contrainte semblable peut être imposée aux estimations des stocks en forçant les niveaux désaisonnalisés à être identiques aux niveaux non désaisonnalisés à un moment précis (p. ex. le 31 décembre). En ce qui concerne la méthode utilisée pour les comptes financiers et du patrimoine, cette contrainte n’est pas rigoureusement appliquée aux totaux annuels, afin de respecter d’autres contraintes. Le tableau 1 résume les caractéristiques communes des données désaisonnalisées et la façon dont elles s’appliquent aux données obtenues au moyen de la méthode d’ajustement saisonnier actuelle des comptes financiers et du patrimoine.
| Caractéristiques | Méthode actuelle |
|---|---|
| La saisonnalité est éliminée | Oui, aucune saisonnalité résiduelle n’est présente dans les stocks du CBN ou les flux du CFF et du ACA. |
| Le total annuel est maintenu | Seulement pour les flux non désaisonnalisés du CFF et du ACA; pour les flux CFF et ACA désaisonnalisés, ceux sans ajustements et ceux ajustés par la désaisonnalisation, la somme pour l’année n’est pas exactement égale, mais ne diffère pas outre mesure. Il s’agissait d’un compromis nécessaire pour respecter d’autres contraintes. |
| Les séries désaisonnalisées recoupent les séries non désaisonnalisées | Oui, dans tous les cas. |
| La relation stocks-flux est respectée pour les données désaisonnalisées (c.-à-d. Lt = Lt-1 + Ft + ACAt) | Oui |
| La méthode pourra être appliquée ultérieurement à d’autres séries des comptes financiers et du patrimoine | Oui |
| Source : Statistique Canada, « Désaisonnalisation des stocks et des flux des comptes financiers et du patrimoine : vers une méthode intégrée », Les nouveautés en matière de comptes économiques canadiens (13-605-X), 2018. | |
Enfin, les comparaisons en glissement annuel sont souvent insuffisantes, car le trimestre de l’année précédente peut contenir un biais saisonnier comparativement au trimestre en cours. Par exemple, la présence d’un jour férié à date non fixe comme le congé de Pâques, peut avoir un impact considérable sur le niveau de chaque trimestre. Aussi, les comparaisons en glissement annuel ont tendance à manquer de rapidité pour identifier les points de retournement (récession ou reprise) lorsque comparées à l’analyse trimestrielle des données corrigées de variations saisonnières.
La séquence suivante résume chaque étape de la méthode intégrée actuelle d’ajustement saisonnier des stocks et des flux des comptes financiers et du patrimoine.
Calcul des stocks, des flux et des autres changements d’actifs désaisonnalisés
Étape 1. Désaisonnalisation d'une version stock d
où,
et,
Note : Les données ACA sont rarement saisonnières, donc
Étape 2. Désaisonnalisation du stock CBN modifié pour exclure le stock ACA
Note : La version modifiée du stock CBN correspond à une version du stock CFF (des flux cumulés de CFF) avec le même niveau de départ que le stock CBN non cumulé.
Étape 3. Calcul des stocks désaisonnalisés du CBN comme la somme des stocks désaisonnalisés et modifiés du CBN et des stocks désaisonnalisés d'ACA
Étape 4. Calcul des flux désaisonnalisés du CFF comme la différence entre les stocks désaisonnalisés et modifiés du CBN de la période actuelle et de la période précédente.
où,
dénote les séries désaisonnalisées
dénote les séries sans ajustements
dénote le processus de désaisonnalisation
- Date de modification :