Estimation de la variance par le bootstrap avec remise pour les enquêtes auprès des ménages Principes, exemples et mise en œuvre
Section 3. Estimation de la variance bootstrap
Nous
commençons à la section 3.1 par la description de l’étape élémentaire de
la méthode bootstrap quand on sélectionne seulement un échantillon de ménages.
Nous l’illustrons dans la section 3.2 sur l’exemple présenté à la
section 2.1.4. La méthode bootstrap en cas d’échantillonnage de personnes
à l’intérieur des ménages est décrite à la section 3.3, et elle est
illustrée à la section 3.4. Dans la section 3.5, nous expliquons
comment l’étape élémentaire de la méthode bootstrap proposée sert à effectuer l’estimation
de la variance et produire des intervalles de confiance.
3.1 Étape élémentaire du bootstrap pour les ménages
Au
moyen du bootstrap avec remise, nous tirons d’abord à l’intérieur de l’échantillon
initial sélectionné dans la strate un rééchantillon avec remise de ménages, avec probabilités égales. Notons que
le rééchantillonnage est effectué sur l’unité d’échantillonnage (un ménage)
plutôt que sur l’unité finale d’observation (une personne), ce qui est
essentiel pour saisir correctement la variance due à l’échantillonnage. En
particulier, cette méthode bootstrap permet de saisir la variance due à l’échantillonnage
du second degré (sélection des personnes) sans rééchantillonner les unités
finales dans le processus de bootstrap. Pour tout nous définissons le facteur d’ajustement de
repondération
avec le nombre de fois que le ménage est sélectionné dans le
rééchantillon également appelé la
multiplicité. Il faut noter qu’une unité peut ne pas apparaître dans le
rééchantillon, auquel cas cette unité a une multiplicité nulle; un exemple est
donné à la section 3.2. Les facteurs d’ajustement de la repondération sont utilisés pour obtenir les
poids bootstrap qui tiennent compte du plan d’échantillonnage, de la
non-réponse totale et du calage, comme le décrit l’algorithme 1. Les
étapes font référence à la figure 2.1. Le rééchantillonnage présenté dans
l’algorithme 1 est ensuite répété fois indépendamment pour l’estimation
de la variance ou pour produire un intervalle de confiance, voir l’algorithme 3
à la section 3.5.
Algorithme 1. Calcul des poids bootstrap des
ménages tenant compte de la non-réponse et du calage
-
Étape 1 : nous tenons
compte de l’échantillonnage des ménages en calculant, pour tout le poids d’échantillonnage
bootstrap
La version bootstrap de l’estimateur
en présence de réponse complète donnée dans (2.3) est
-
Étape 2 : nous tenons
compte de la non-réponse totale des ménages en calculant les probabilités
estimées bootstrap à l’intérieur des GRH.
et nous calculons les poids
bootstrap corrigés pour tenir compte de la non-réponse
avec le GRH contenant le ménage La version bootstrap de l’estimateur corrigé
pour tenir compte de la non-réponse totale donnée dans (2.7)
est
-
Étape 3 : nous tenons
compte du calage en calant les poids sur les totaux Cela donne les poids bootstrap
calés
avec
et
La version bootstrap de l’estimateur
calé donnée dans (2.10) est
Le traitement de la non-réponse
totale dans le processus bootstrap mérite quelques explications. Premièrement,
notre approche est conditionnelle aux indicateurs de réponse Contrairement aux indicateurs d’appartenance
de l’échantillon qui sont traités par bootstrap à l’étape 1 de l’algorithme 1,
les indicateurs de réponse demeurent fixes dans le processus bootstrap. Cela
est dû au fait que nous cherchons à reproduire un estimateur de la variance qui
considère l’échantillon comme étant sélectionné avec remise, et que
dans ce cas, il n’est pas nécessaire d’appliquer la technique bootstrap aux Deuxièmement, la prise en compte de la non-réponse à l’étape 2 de l’algorithme
1 est réalisée conditionnellement sur les GRH : nous n’appliquons pas de
bootstrap au processus menant à la construction des GRH (sur le sujet, voir par exemple
Girard, 2009; Haziza et Beaumont, 2017). Enfin, le bootstrap des probabilités
de réponse tel qu’il est décrit dans l’équation (3.4) tient compte de l’estimation
des probabilités de réponse En d’autres termes, nous utilisons dans chaque
rééchantillonnage les mêmes GRH que ceux déterminés à partir de l’échantillon,
mais les ajustements pour tenir compte de la non-réponse dans les GRH sont
basés sur le contenu du rééchantillonnage. Cela est illustré dans l’exemple
présenté à la section 3.2. Si nous n’appliquons pas de bootstrap aux
probabilités de réponse et que nous insérons directement dans l’équation (3.5)
les probabilités estimées à l’origine alors les probabilités de réponse sont
traitées comme si elles étaient connues, ce qui entraîne habituellement une
surestimation de la variance (Beaumont, 2005; Kim et Kim, 2007).
Discutons maintenant de l’estimation
de la variance bootstrap pour les estimateurs calés, comme cela est fait à l’étape 3
de l’algorithme 1 où l’étape de calage est réalisée sur le total réel de
la population Si l’on suit le principe bootstrap selon
lequel l’échantillon est à l’échantillon bootstrap ce que la population est à l’échantillon il pourrait sembler plus intuitif de caler
plutôt les totaux estimés obtenus en insérant dans l’équation (2.3). Les deux démarches
semblent valides pour ce qui est de l’estimation de la variance bootstrap pour
l’estimateur calé mais les variables de calage peuvent être sujettes à la non-réponse sur l’échantillon
ce qui rend l’estimateur impossible à calculer, alors que le total est connu à partir d’une source extérieure.
3.2 Exemple de calcul des poids bootstrap des ménages
Nous poursuivons avec l’exemple
présenté à la section 2.1.4. On réalise le bootstrap en sélectionnant d’abord
un rééchantillon de ménages, avec remise et probabilités égales,
parmi les ménages initialement échantillonnés. Dans cet exemple, nous supposons
que le ménage est sélectionné trois fois, que le ménage est sélectionné deux fois et que les ménages et sont sélectionnés une fois. Au moyen de l’équation (3.2),
on obtient les poids d’échantillonnage bootstrap
Les poids d’échantillonnage bootstrap sont corrigés pour
tenir compte de la non-réponse de la même façon que dans la correction initiale
de la non-réponse, au moyen des mêmes GRH et des probabilités estimées
pondérées. Dans ce cas, le premier GRH contient uniquement l’unité qui est un répondant, de sorte
que Le second GRH contient (non-répondant), et Cela donne
et les poids bootstrap corrigés pour
tenir compte de la non-réponse
Enfin, les poids sont calés pour qu’ils
soient appariés à la taille de la population et au total auxiliaire Cela donne les poids bootstrap
calés
Le calcul des poids bootstrap est résumé
à la figure 3.1.
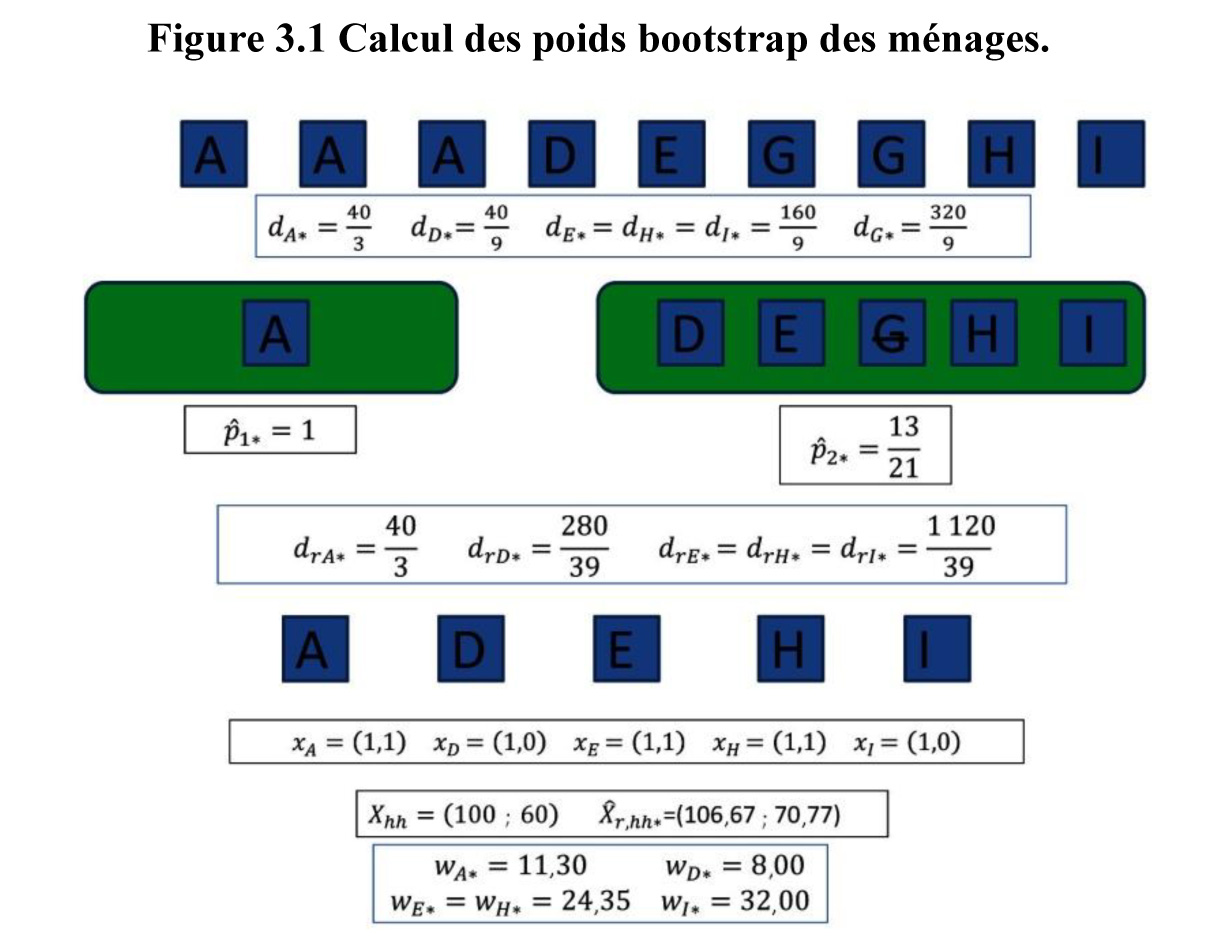
Description de la figure 3.1
Figure
résumant la section 3.2, soit calcul des poids bootstrap des ménages avec
un exemple. La figure illustre à l’aide d’un exemple les étapes expliquées à la
section 3.1. Dans cet exemple, nous poursuivons avec l’exemple présenté à
la section 2.1.4. On réalise le bootstrap en sélectionnant d’abord un rééchantillon
de 9 ménages, avec remise et probabilités égales, parmi les ménages
initialement échantillonnés. Dans cet exemple, nous supposons que le ménage A
est sélectionné trois fois, que le ménage G (non-répondant) est sélectionné
deux fois et que les ménages D, E, H et I sont sélectionnés une fois.
3.3 Calcul des poids bootstrap pour les personnes
Le
calcul des poids bootstrap tenant compte du plan d’échantillonnage, de la
non-réponse des ménages et des personnes et du calage est décrit dans l’algorithme 2.
Les étapes font référence à la figure 2.3. En plus des étapes de bootstrap
de l’algorithme 1, notons que l’algorithme 2 implique le calcul
bootstrap des probabilités de réponse individuelles uniquement. Ajoutons que le
sous-échantillonnage des personnes à l’intérieur des ménages n’a pas besoin d’être
traité par bootstrap, comme nous l’indiquons à la section 3.1.
Algorithme 2. Calcul des poids
individuels bootstrap tenant compte de la non-réponse des ménages, de la
non-réponse des personnes et du calage
-
Exécuter les étapes 1 et 2 de
l’algorithme 1. Les poids bootstrap des ménages corrigés pour tenir compte
de la non-réponse sont selon l’équation (3.5).
-
Étape 3b : nous tenons d’abord
compte de l’échantillonnage des personnes en calculant les poids bootstrap
individuels corrigés pour tenir compte de la non-réponse totale du ménage.
avec
le ménage contenant
Nous
tenons ensuite compte de la non-réponse totale des personnes. Nous calculons
les probabilités estimées bootstrap à l’intérieur des GRH.
Nous
calculons les poids bootstrap des personnes avec correction pour tenir compte
de la non-réponse du ménage ou d’une personne, à savoir :
avec le GRH contenant la personne La version bootstrap de l’estimateur
corrigé pour tenir compte de la non-réponse totale donnée dans (2.27) est
-
Étape 4b : nous tenons
compte du calage en calant les poids sur les totaux Cela donne les poids bootstrap
calés
avec
et
La version
bootstrap de l’estimateur calé donnée dans (2.29) est
3.4 Exemple de calcul des poids bootstrap des
personnes
Nous
poursuivons avec l’exemple présenté à la section 3.2. L’échantillon
bootstrap de ménages est constitué de (trois fois), (deux fois), et et (une fois). En raison de la non-réponse des
ménages, nous observons et seulement. À partir de (2.30), on obtient l’échantillon
bootstrap de personnes
Les poids bootstrap des ménages
corrigés pour tenir compte de la non-réponse totale sont donnés dans l’équation
(3.11). À partir de l’équation (3.13), les poids bootstrap des personnes
ajustés pour tenir compte de la non-réponse des ménages sont
Ces
poids bootstrap sont corrigés pour tenir compte de la non-réponse des personnes
de la même façon que dans la correction initiale de la non-réponse
individuelle, au moyen des mêmes GRH et des probabilités estimées non
pondérées. Cependant, nous devons tenir compte dans ces probabilités de la
multiplicité et du facteur d’ajustement de la repondération
voir l’équation (3.1). Dans notre cas, le
premier GRH contient les personnes et et est un non-répondant. La personne appartient au ménage qui a été sélectionné trois fois dans l’échantillon bootstrap. La personne appartient au ménage et la personne appartient au ménage qui ont tous deux été sélectionnés une fois
dans l’échantillon bootstrap Le calcul est semblable pour le second GRH et donne
et les poids bootstrap des personnes
corrigés pour tenir compte de la non-réponse du ménage ou de la personne sont
donnés par
Enfin, les poids sont calés pour qu’ils
permettent de reproduire exactement la taille de la population et le total auxiliaire Cela donne les poids bootstrap
calés
Le calcul des poids bootstrap des
personnes est résumé à la figure 3.2.
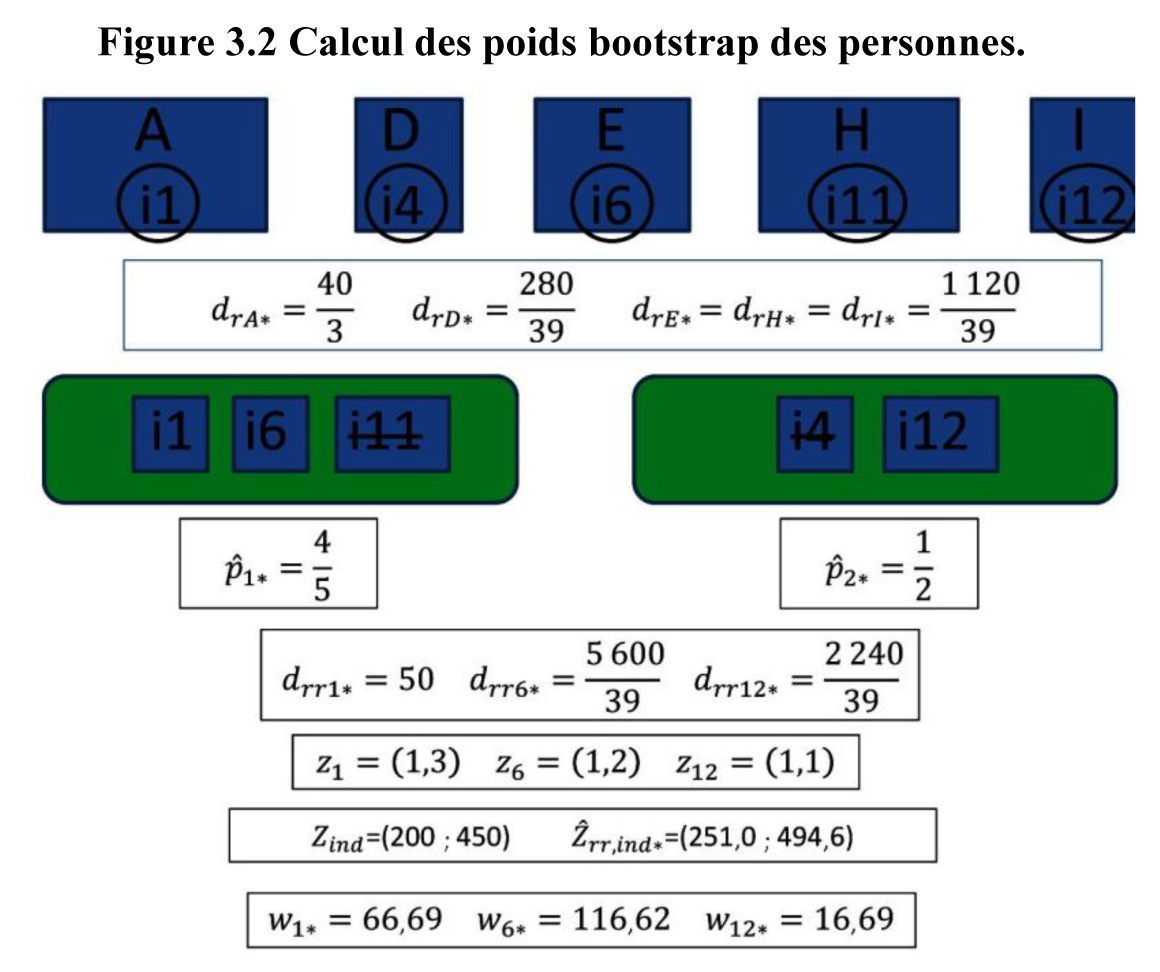
Description de la figure 3.2
Figure
résumant la section 3.4, soit calcul des poids bootstrap des personnes dans
un exemple. La figure illustre à l’aide d’un exemple les étapes expliquées à la
section 3.3. Dans cet exemple, nous poursuivons avec l’exemple présenté à
la section 3.2. L’échantillon bootstrap de ménages est constitué de A
(trois fois), G (deux fois), et D, E, H et I (une fois). En raison de la
non-réponse des ménages, nous observons A, D, E, H et I seulement. Les
personnes sélectionnées sont
et
mais
et
sont non-répondants.
3.5 Estimation de la variance bootstrap et
intervalles de confiance
Dans la
présente section, nous nous intéressons aux paramètres qui peuvent être écrits
comme des fonctions lisses de totaux. Nous expliquons comment l’étape
élémentaire de la méthode bootstrap proposée sert à effectuer l’estimation de
la variance et produire des intervalles de confiance. Par souci de concision,
nous nous concentrons sur les paramètres définis sur la population de ménages Le traitement des paramètres d’intérêt dans la
population de personnes est semblable.
Supposons
que est un vecteur de taille de variables d’intérêt, et que nous nous
intéressons à un paramètre utilisant une fonction connue et lisse En cas de réponse complète, l’estimateur par substitution de est
voir, par exemple, Deville (1999). En
cas de non-réponse totale au niveau du ménage, l’estimateur de corrigé pour tenir compte de la
non-réponse totale est
et l’estimateur calé de est
Dans
chaque cas, on obtient un estimateur de la variance bootstrap en appliquant un
grand nombre de fois (disons l’étape de base de la méthode bootstrap dans l’algorithme 1,
puis en calculant la dispersion des estimateurs bootstrap. Cela est résumé dans
l’algorithme 3.
Algorithme 3. Estimation de la variance
bootstrap pour l’estimation de la population des ménages
- Répéter
fois la procédure bootstrap
décrite dans l’algorithme 1. Soit et les estimateurs bootstrap des
totaux calculés sur le -ème échantillon. De plus,
désignons par et les estimateurs bootstrap
associés à
- L’estimateur de la variance bootstrap pour
est
et de même
pour et
L’estimateur
de la variance bootstrap peut servir à calculer un intervalle de confiance
reposant sur la normalité avec un niveau ciblé Par exemple, l’intervalle de confiance quand
on utilise l’estimateur en présence de réponse complète est
avec le quantile d’ordre de la distribution normale
standard. On s’attend à ce que cet intervalle de confiance soit conservatif,
puisque la méthode bootstrap proposée l’est.
Nous
examinons aussi les intervalles de confiance bootstrap (aussi dits
élémentaires) dites du percentile et du percentile inverse. Ils peuvent être
calculés directement à partir des poids bootstrap et sont par conséquent
intéressants du point de vue des utilisateurs des données, contrairement aux
méthodes nécessitant une grande puissance de calcul comme le bootstrap (par exemple Davison et Hinkley, 1997;
Shao et Tu, 1995). Pour l’intervalle de confiance percentile est
obtenu au moyen de la distribution de comme approximation de la distribution de Cette méthode utilise les estimations
bootstrap ordonnées pour former l’intervalle de confiance
avec le niveau ciblé où et On obtient l’intervalle de
confiance percentile inverse en considérant la distribution de comme une approximation de la
distribution de Cela donne l’intervalle de
confiance
Les propriétés de l’estimateur de la
variance bootstrap et des trois intervalles de confiance sont évaluées dans l’étude
par simulations effectuée à la section 4 pour l’estimation d’un total.
Le
choix du nombre de rééchantillonnages constitue un problème
pratique important. Girard (2009) propose d’envisager plusieurs tailles de rééchantillonnage
possibles (par exemple en augmentant par un incrément de 100) et de représenter
graphiquement les estimateurs de la variance bootstrap en fonction de La valeur pour laquelle cet estimateur de la
variance commence à se stabiliser est alors retenue. Il s’agit d’une méthode
simple, mais qui peut nécessiter une solution de compromis si différentes
variables d’intérêt donnent différentes valeurs de stabilisation. Beaumont et
Patak (2012) proposent de choisir de telle sorte qu’avec une forte probabilité,
la longueur de l’intervalle de confiance bootstrap donnée dans (3.28) soit
proche de la longueur de l’intervalle de confiance obtenu au moyen d’un
estimateur de la variance analytique. En supposant que, conditionnellement à l’échantillon
initial, l’estimateur bootstrap normalisé du total est normalement distribué,
ils établissent que la valeur peut être déterminée à partir de la
distribution d’une variable du chi deux (Beaumont et Patak, 2012,
équation 10). Il est intéressant d’observer que la valeur obtenue ne
dépend pas de la variable d’intérêt. À partir de ces résultats, ils proposent d’utiliser
une valeur qui ne soit pas inférieure à 750 et une
valeur plus grande si l’hypothèse de normalité de l’estimateur bootstrap peut
ne pas se vérifier. Nous avons utilisé 1 000 dans l’étude par simulations présentée dans la section
suivante. Pour les enquêtes devant répondre à plusieurs besoins
analytiques allant de paramètres de population
simples à complexes et à diverses tailles de domaine la sélection d’au moins
1 000 répliques est la norme compte tenu des ressources informatiques
disponibles à l’heure actuelle.

