3. L’estimation de la fonction de densité des revenus

Eric Graf et Yves Tillé

Précédent | Suivant

Dans une approche basée sur le plan (design based) en population finie, l’inférence se fait par rapport au plan de sondage $P(S)$  utilisé pour sélectionner l’échantillon $S$  dans la population $U$  de taille finie $N$ . Dans cette approche, seules les indicatrices d’inclusion dans l’échantillon sont aléatoires, toutes les autres grandeurs sont fixes. La fonction de répartition des revenus au niveau de la population est alors une fonction en escaliers : $F_y\left(x\right)={\displaystyle {\sum }_{{}_{k\in U}}{1}_{y_k\le x}}/N$ et sa dérivée, la fonction de densité, n’existe pas à cause des discontinuités. Si l’on ne veut pas se placer dans une approche basée sur le modèle (model based) avec un modèle de super population pour justifier le terme de fonction de densité des revenus, il faut artificiellement lisser la fonction de répartition pour qu’elle devienne dérivable. C’est donc par abus de langage que nous nous autorisons ici à parler de fonction de densité. Avec cette volonté de lissage, Deville (2000) et Osier (2009) proposent d’estimer la fonction de densité des revenus par noyau gaussien :

$$\begin{array}{lll}K\left(u\right)\hfill & =\hfill & \frac{1}{h\sqrt{2\pi }}{e}^{-u^2/2}\mathrm{,}u=\frac{x-y_k}{h}\hfill \\ {\widehat{f}}_1\left(x\right)\hfill & =\hfill & \frac{1}{\widehat{N}}{\displaystyle \sum _{k\in S}}{w}_{k}K\left(\frac{x-y_k}{h}\right)\left(3.1\right)\hfill \\ \hfill & =\hfill & \frac{1}{h\sqrt{2\pi }}\frac{1}{\widehat{N}}{\displaystyle \sum _{k\in S}}{w}_k\exp \left[-\frac{{\left(x-y_k\right)}^2}{2h^2}\right]\hfill \end{array}$$

où $h$  est la largeur de la bande qu’Osier estime par $\widehat{h}=\widehat{\sigma }{\widehat{N}}^{-\text{0,2}}$  et $\widehat{\sigma }$  est l’écart-type estimé de la distribution empirique des revenus :

$$\widehat{\sigma }=\sqrt{\frac{{\displaystyle {\sum }_{k\in S}{w}_k{y}_k^2}}{\widehat{N}}-{\left(\frac{{\displaystyle {\sum }_{k\in S}{w}_k{y}_k}}{\widehat{N}}\right)}^2}=\sqrt{\frac{{\displaystyle {\sum }_{k\in S}{w}_k{y}_k^2}}{\widehat{N}}-{\overline{y}}_w^2}\mathrm{.}$$

Notons que cette estimation de $\sigma$  n’est pas robuste étant très sensible aux valeurs extrêmes de $y.$  Des données de revenus ont très souvent une queue de distribution étendue vers la droite avec des valeurs très élevées possibles, on parle de valeurs aberrantes représentatives (representative outliers) au sens de Chambers (1986) et Hulliger (1999). Comme le montrent nos simulations dans la section 4, cela peut fortement biaiser nos estimations de variance. Verma et Betti (2011) procèdent également par noyau rappelant que, selon Silverman (1986), le choix du noyau n’est pas crucial pour assurer la convergence de $\widehat{f}\left(y\right)$  vers $f\left(y\right),$  alors que celui de la largeur de bande l’est. Ils utilisent une valeur conseillée par Silverman dans le cas de distributions avec un coefficient d’asymétrie positif, $h=\text{0,79(}{\widehat{Q}}_{75}-{\widehat{Q}}_{25}){\widehat{N}}^{-\text{0,2}}.$  Dans leurs conclusions, ils relèvent que la méthode par linéarisation peut être problématique en raison d’irrégularités de la fonction de densité empirique. On ajoutera que ces problèmes sont d’autant plus préoccupants qu’il est fréquent, dans les données issues d’enquêtes, d’avoir des agglomérats d’observations à certaines valeurs (dues à des arrondis ou des questions-fourchettes), ce qui peut compliquer l’estimation de la densité. La suite de l’article décrit des solutions que nous avançons pour réduire le biais de la variance estimée.

3.1 Passer par le logarithme

Une solution qui, comme on le verra plus loin, donne de très bons résultats est de simplement passer par le logarithme pour estimer la densité en $x.$  Si l’on pose $v=\log \left(x+a\right),$  où $x$  est le revenu et $a$  un nombre réel positif par exemple égal à $\left(\left|{{\displaystyle \min }}_k(y_k)\right|+1\right)$  dans le cas où l’on aurait des revenus négatifs ou nuls (en négligeant le fait que $a$  serait estimé), on a que

$$F_v\left(v\right)=P\left(\mathcal{V}\le v\right)=P\left(\log \left(\mathcal{Y}+a\right)\le v\right)=P\left(\mathcal{Y}\le e^v-a\right)=F_y\left(e^v-a\right)\mathrm{,}$$

où $\mathcal{V}$  et $\mathcal{Y}$  seraient de variables aléatoires. Donc,

$$f_v\left(v\right)=\frac{d{F}_v\left(v\right)}{dv}=\frac{d{F}_y\left(e^v-a\right)}{dv}=f_y\left(e^v-a\right)e^v\mathrm{.}$$

Autrement dit $f_v\left(v\right)=f_y\left(x\right)\left(x+a\right),$  ce qui nous donne l’estimateur suivant de la densité en $x:$

$${\widehat{f}}_2\left(x\right)=\frac{{\widehat{f}}_v\left(v\right)}{x+a}=\frac{{\widehat{f}}_y\left(\log \left(x+a\right)\right)}{x+a}\mathrm{.}\left(3.2\right)$$

L’estimation de la densité en $x$  de $\mathcal{Y}$  peut donc s’évaluer en estimant celle du logarithme de la variable, divisée par la valeur de la variable au point qui nous intéresse. La propriété reste valable en population finie. Le fait de passer par le logarithme a l’avantage de diminuer l’effet levier exercé par les grandes valeurs des revenus dans le calcul de l’approximation de la densité par noyau. Les simulations montrent que cette méthode très simple réduit fortement le biais.

3.2 Plus proches voisins avec largeur de bande minimale

Deville (2000) esquisse une autre manière du type « plus proches voisins » (voir Silverman 1986) d’estimer la densité en utilisant le noyau

$$K_D\left(u\right)=\{\begin{array}{ll}\frac{1}{b-a}\hfill & \text{si}a\le u\text{<}b\hfill \\ 0\hfill & \text{sinon}\mathrm{,}\hfill \end{array}\mathrm{,}$$

avec $u=y_k$  et où le choix de $a$  et $b,$  vérifiant $x\in \left[a,b\right],$  reste à déterminer et pourrait dépendre de $x.$  La distance $\left(b-a\right)$  représente la largeur de bande $h.$  L’estimation de la densité vaudrait alors

$$\begin{array}{lll}{\widehat{f}}_D\left(x\mathrm{,}a\mathrm{,}b\right)\hfill & =\hfill & \frac{1}{\widehat{N}}{\displaystyle \sum _{k\in S}}{K}_D\left(y_k\right)\hfill \\ \hfill & =\hfill & \frac{1}{\widehat{N}}{\displaystyle \sum _{k\in S}}{w}_k\frac{1}{b-a}{1}_{y_k\in \left[a\mathrm{,}b\right[}\left(3.3\right)\hfill \\ \hfill & =\hfill & \frac{{\widehat{F}}_y\left(b\right)-{\widehat{F}}_y\left(a\right)}{b-a}\mathrm{,}x\in \left[a\mathrm{,}b\right[\hfill \end{array}$$

avec ${\widehat{F}}_y\left(x\right)={\displaystyle {\sum }_{k\in S}{w}_k{1}_{y_k\le x}/\widehat{N}}.$

Notons que l’estimation de la densité (3.3) n’est pas une fonction continue et qu’elle ne serait pas très adaptée pour estimer des valeurs de densité à l’extrémité des queues de la distribution. Puisque nos travaux ne reposent pas trop sur les queues de la distribution, nous considérons cette approche comme une option.

Notre deuxième proposition d’estimation de la densité en $x$  s’inspire de l’idée ci-dessus. Elle est du type « plus proches voisins », mais impose aussi une largeur de bande minimale : notre méthode impose d’utiliser au minimum les $p$  plus proches observations du point $x$  tout en imposant une largeur de bande minimale $h(p)\ge h_{\text{opt}}$  où

$$h_{\text{opt}}=\frac{\text{0,9}\min (\widehat{\sigma }\mathrm{,}{\widehat{Q}}_{75}-{\widehat{Q}}_{25})}{\text{1,34}\sqrt[5]{\widehat{N}}}$$

est la règle empirique (rule of thumb) de Silverman (1986) pour déterminer la largeur de la bande. Cette valeur est aussi utilisée par défaut par la fonction R density pour la largeur de la bande si rien n’est spécifié. Cette solution est plus robuste que (3.1) et évite les problèmes que l’on rencontre lorsque plusieurs valeurs $y_k$  sont très proches les unes des autres, ce qui arrive fréquemment parce que les personnes interrogées ont tendance à arrondir leur revenu.

Les valeurs $y_k,$   $k=1,\mathrm{...},n,$  étant supposées ordonnées par leur rang, la largeur $h\left(p\right)$  de la fenêtre autour de $x$  est initialement déterminée par les $p$  plus proches observations, avec $p\ll n.$  Pour les simulations exposées dans la section suivante, après différents essais, le $p$  initial a été fixé à 30. On impute comme densité en $x$  la densité estimée au point observé $y_j$  le plus proche inférieur ou égal à $x,$  c’est-à-dire $j=\max \left(k|y_k\le x\right),$   $k=1,\mathrm{...},n.$  La largeur de la bande en $x$  dépendra en fait des $p_j$  plus proches observations autour de $y_j,$  avec $p_j\ge p.$  On la désignera par $h\left(p_j\right)$  dans la suite pour le rappeler. La densité n’est donc estimée qu’en des points observés sans qu’un lissage ou une interpolation soient menés entre les $\widehat{f}\left(y_j\right).$  L’algorithme pour estimer $\widehat{f}\left(y_j\right)$  est le suivant (voir aussi Figure 3.1) :

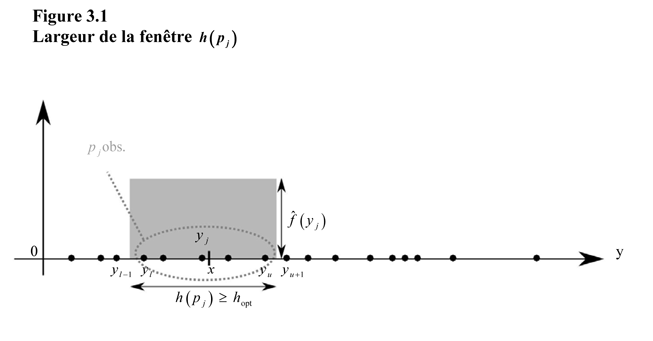
1. La largeur initiale de la fenêtre autour du point $y_j,$  avec $p_j=p,$  est définie par :

$$\begin{array}{llll}h\left(p_j\right)=\frac{y_u+y_{u+1}}{2}-\frac{y_{\ell }+y_{\ell -1}}{2};\hfill & u\hfill & =\hfill & \{\begin{array}{ll}j+p_j/2-1\hfill & \text{si}{p}_j\text{est}\text{pair}\hfill \\ j+\lfloor p_j/2\rfloor \hfill & \text{si}{p}_j\text{est}\text{impair}\hfill \end{array}\hfill \\ \hfill & \ell \hfill & =\hfill & j-\lfloor p_j/2\rfloor \mathrm{.}\hfill \end{array}$$

2. Si la largeur de fenêtre $h(p_j)$  ainsi obtenue est inférieure à $h_{opt}$ , on incrémente les deux bornes :

borne supérieure : $u\to u+1,$  tant que $u\text{<}n,$

borne inférieure : $l\to l-1,$  tant que $l\text{>}1,$

ce qui implique $p_j\to p_j+2,$ nbsp;sauf si $u=n$  ou $l=1,$  on n’a alors plus le même nombre de points à gauche et à droite de $y_j.$

3. Répéter 2 jusqu’à ce que $h\left(p_j\right)\ge h_{\text{opt}}.$

4.   La densité estimée en $x$  est alors donnée par

$$\widehat{f}\left(x\right)=\widehat{f}\left(y_j\right)=\{\begin{array}{ll}\frac{p_j}{nh\left(p_j\right)}\hfill & \text{sans}\text{pondération}\mathrm{,}\hfill \\ \frac{{\displaystyle \sum _{p_j\text{plus}\text{proche}s\text{de}{y}_j}}{w}_j^{\text{std}}}{nh\left(p_j\right)}\hfill & \text{avec}\text{pondération}\mathrm{,}\hfill \end{array}$$

avec les poids standardisés $w_k^{\text{std}}=w_k/\overline{w},$   $k=1,\mathrm{...},n.$

Le nombre d’observations $p_j$  prises en compte pour le calcul peut varier et dépend de la courbure locale de la fonction de répartition empirique. La condition $h(p_j)\ge h_{opt}$  garantit une largeur de fenêtre minimale aux endroits où beaucoup d’observations seraient concentrées sur un petit intervalle. On rend la procédure encore plus solide en combinant cette approche avec la précédente, c’est-à-dire en estimant la densité du logarithme de la variable divisée par sa valeur (non logarithmisée) :

$${\widehat{f}}_3\left(x\right)=\frac{\widehat{f}\left(\text{log}\left(x+a\right)\right)}{x+a}\mathrm{.}\left(3.4\right)$$

3.3 Robustesse de la linéarisée

Comme mentionné plus haut, dans le cas de la médiane ou pour les autres quantiles, Croux (1998) relève que la fonction d’influence empirique ou linéarisée estimée à partir de l’échantillon n’est pas aussi robuste qu’il n’y paraît, même si l’on connaît la fonction de densité. Nous avons vérifié cela pour les données SILC utilisées dans les simulations modélisées avec une loi Bêta Généralisée de seconde espèce (GB2) grâce à la fonction profml.gb2 de R (Graf et Nedyalkova 2011). Sur de petits échantillons $\left(n\le 100\right),$  le biais potentiel de la linéarisée engendré par un trop grand nombre de valeurs extrêmes peut aussi biaiser l’estimation de la variance calculée à partir de cette dernière. Pour de plus grands échantillons $\left(n\ge 1000\right),$  un biais relatif maximal dans la variance estimée à l’aide de la linéarisée empirique vs. théorique peut atteindre jusqu’à 5 %. Il est cependant en-dessous du pourcent en valeur absolue dans les trois quarts des cas.

Précédent | Suivant