Publications

Série de documents de recherche sur l'analyse économique

11F0027M, n^o 91
Publié en mai 2014

La distribution des taux de croissance de l’emploi au Canada : le rôle des entreprises à forte croissance et à réduction rapide des effectifs

La distribution des taux de croissance de l'emploi au Canada : le rôle des entreprises à forte croissance et à réduction rapide des effectifs

Warning Consulter la version la plus récente.

Information archivée dans le Web

L’information dont il est indiqué qu’elle est archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Elle n’est pas assujettie aux normes Web du gouvernement du Canada et elle n’a pas été modifiée ou mise à jour depuis son archivage. Pour obtenir cette information dans un autre format, veuillez communiquer avec nous.

par Jay Dixon et Anne-Marie Rollin

Passer au texte

Résumé
Sommaire
1 Introduction
2 Contexte
3 Données et mesures
4 Distribution des taux de croissance de l'emploi au Canada
5 Contributions des entreprises à forte croissance et des entreprises à réduction rapide des effectifs
6 Cadre de la régression quantile
7 Résultats des régressions quantiles
8 Conclusion
9 Annexe
Notes

Début du texte

Résumé

La présente étude s’appuie sur des données provenant de la base de données du Programme d’analyse longitudinale de l’emploi de Statistique Canada pour examiner la distribution des taux de croissance de l’emploi au Canada de 2000 à 2009, en se concentrant surtout sur les entreprises situées dans les queues de la distribution, appelées ici entreprises à forte croissance (EFC) et entreprises à réduction rapide des effectifs (ERR).

L’étude a trois objectifs. Le premier consiste à décrire les distributions des taux de croissance de l’emploi au Canada afin de voir si elles concordent avec celles observées dans d’autres pays. Le deuxième consiste à quantifier la contribution des EFC et des ERR à la création ainsi qu’à la destruction agrégées des emplois. Enfin, le troisième consiste à examiner, en faisant appel à des techniques de régression quantile, le rôle de la taille et de l’âge des entreprises dans le rendement des EFC et des ERR.

Les résultats montrent que, comme dans d’autres pays, la densité des distributions des taux de croissance de l’emploi au Canada est plus forte au centre et dans les queues que celle de la distribution normale. Même si la plupart des entreprises changent peu leur effectif d’une année à l’autre, celles qui croissent ou qui rapetissent rapidement représentent une part importante de l’emploi créé et de l’emploi détruit chaque année. Enfin, une petite taille d’entreprise est un prédicteur plus important que l’âge dans le cas des ERR, tandis que l’âge de l’entreprise, plus précisément le jeune âge, est un meilleur prédicteur que la taille pour les EFC. Quel que soit leur âge, les petites entreprises sont plus susceptibles que les autres d’éliminer d’une année à l’autre une part importante de leur effectif, tandis que, quelle que soit leur taille, les jeunes entreprises sont plus susceptibles que les autres d’afficher des taux de croissance annuels élevés.

Sommaire

Les discussions du grand public sur la croissance des entreprises s’appuient surtout sur des histoires de croissance et de déclin rapide. En revanche, les études empiriques de la dynamique des entreprises sont axées sur la croissance moyenne, ou représentative, des entreprises. En faisant appel aux méthodes économétriques classiques, telles que la régression linéaire, elles visent à déterminer comment les caractéristiques de l’entreprise, dont la taille et l’âge, influent sur les tendances centrales des distributions de la croissance. Ces méthodes ne tiennent pas compte de l’influence des entreprises qui croissent ou rapetissent rapidement, ou elles sont ajustées de manière à réduire au minimum cette influence. Cependant, comme ces entreprises pourraient être à l’origine d’une part importante de la dynamique de l’emploi dans l’économie, cette minimisation est inappropriée.

Le présent document explore la contribution des entreprises à forte croissance (EFC) et des entreprises à réduction rapide des effectifs (ERR) à la croissance nette de l’emploi en se servant des données du Programme d’analyse longitudinale de l’emploi (PALE) de Statistique Canada. Après avoir décrit la distribution des taux de croissance de l’emploi, on aborde la question de savoir si les EFC et les ERR ont effectivement joué un rôle d’une importance disproportionnée dans la création et dans la destruction de l’emploi au Canada de 2000 à 2009. On examine ensuite l’influence des caractéristiques de l’entreprise, en particulier l’industrie, la taille et l’âge, sur la forte croissance ou le déclin rapide.

L’ensemble de données du PALE présente certains avantages comparativement aux données utilisées dans d’autres études de la croissance des entreprises. Dans la plupart des ensembles de données, la couverture des entreprises selon l’industrie ou selon la taille est limitée, tandis que le PALE englobe toutes les entreprises ayant des employés au Canada. Mais surtout, alors que la plupart des études portent sur la croissance totale des entreprises, y compris le transfert d’emplois à la suite de fusions et d’acquisitions, la structure du PALE permet d’isoler la création ou la destruction nette d’emplois, c’est-à-dire la croissance organique, au niveau de l’entreprise.

L’étude montre que la distribution de la croissance des entreprises passe par un sommet autour de l’origine, mais que sa densité dans les extrémités est plus forte que celle de la distribution normale. La forme de la distribution reflète le fait que, pour la plupart des entreprises, la croissance organique est faible, quel que soit l’industrie, la taille ou l’âge. Par ailleurs, un petit nombre d’entreprises dont le taux de croissance ou de destruction de l’emploi est très élevé expliquent une part disproportionnée de la dynamique globale de l’emploi dans l’économie canadienne. Les régressions quantiles révèlent que l’âge est un déterminant de la forte croissance : quelle que soit leur taille, les jeunes entreprises sont plus susceptibles que les autres d’afficher des taux de croissance élevés. Par contre, la taille est un déterminant de la probabilité du déclin, les petites entreprises étant plus susceptibles que les autres de réduire rapidement leurs effectifs.

La contribution du présent document aux travaux sur la croissance des entreprises est triple. De très nombreuses études portent sur les courbes moyennes de croissance. La présente étude montre que les tendances moyennes chez les entreprises canadiennes sont régies par les queues de la distribution de la croissance, ce qui concorde avec les constatations faites pour d’autres pays.

En outre, l’étude relie non seulement la forte croissance, mais aussi le déclin rapide, aux caractéristiques de l’entreprise en utilisant des méthodes de régression quantile. Des travaux de plus en plus nombreux sur les entreprises à forte croissance (EFC) et les publications connexes sur les gazelles et l’esprit d’entreprise s’intéressent aux entreprises qui se situent dans la queue positive de la distribution. Ces travaux de recherche font habituellement appel à des études de cas d’entreprises particulièrement en vue, ou à la définition arbitraire de seuils de croissance et à la description des caractéristiques moyennes des entreprises qui les dépassent. En revanche, l’étude des entreprises qui réduisent rapidement leurs effectifs (ERR) a été en grande partie négligée. La présente étude s’appuie sur la régression quantile pour examiner les caractéristiques des entreprises le long de la distribution complète des résultats de croissance, y compris les EFC et les ERR, sans qu’il soit nécessaire de définir des seuils de croissance arbitraires.

1 Introduction

En 1999, une petite société Internet en démarrage et inconnue a déménagé ses huit employés d’un garage dans de nouveaux bureaux. En 2004, la société Google n’était plus en démarrage et n’était plus inconnue. Il ne s’agissait plus non plus d’une petite entreprise, son effectif étant alors de 3 021 employés. En 2010, Google comptait 24 400 employés à plein temps dans le monde entier, et un an plus tard, leur nombre était passé à 32 467¹.

Au Canada, l’essor de Research In Motion (RIM) n’a pas été aussi météorique, mais la société a néanmoins vu croître son effectif à un taux annualisé moyen supérieur à 35 %, pour passer de 200 employés en 1998 à 17 000 en 2012². Une autre entreprise canadienne du secteur de la haute technologie, Nortel, a suivi un chemin différent, réduisant son effectif qui comptait quelque 90 000 employés au taux moyen de 17 % par année de 2000 à 2005, avant de déclarer faillite à la fin de la décennie³.

Les témoignages de croissance et de déclin rapides sont de parfaits exemples des discussions du grand public au sujet de la croissance des entreprises. L’essor de sociétés telles que Google et RIM, et le déclin de Nortel, ont fait connaître ces entreprises de tous. Les expériences qu’elles ont vécues ont également transformé visiblement leur secteur d’activité.

Aussi importantes que ces entreprises paraissent être pour l’économie, elles posent un défi aux chercheurs. La plupart des études de la dynamique des entreprises sont axées sur les tendances centrales des distributions de la croissance. Fondées sur des méthodes telles que la régression linéaire, ces études visent à examiner comment les caractéristiques de l’entreprise, dont la taille et l’âge, influencent, en moyenne, la croissance des entreprises. Cependant, ces méthodes statistiques ne tiennent pas compte de l’influence d’entreprises telles que RIM et Nortel, ou elles sont améliorées de manière à réduire au minimum cette influence.

Pourtant, comme ce genre d’entreprises pourraient être à l’origine d’une part importante de la dynamique de l’emploi étudiée, il semble inapproprié de minimiser leur influence. Les entreprises les plus intéressantes sur le plan de l’innovation et de la répartition des ressources en vue d’augmenter la productivité ne se retrouvent vraisemblablement pas parmi celles dont les résultats sont moyens. Elles font plutôt partie des entreprises qui croissent ou rapetissent rapidement, c’est-à-dire celles qui se situent dans les queues des distributions de la croissance.

Des études de plus en plus abondantes sur les entreprises à forte croissance (EFC) et les études connexes sur les gazelles et l’esprit d’entreprise ont pour objet de repérer et d’analyser les entreprises qui se situent dans la queue positive de la distribution. Elles s’appuient habituellement sur des études de cas d’entreprises particulièrement en vue, ou sur la définition de seuils de croissance arbitraires et la description des caractéristiques moyennes des entreprises qui dépassent ces seuils. Si ces deux approches révèlent des détails du processus de croissance, elles ne remplacent pas l’analyse statistique rigoureuse.

En outre, peu de travaux de recherche ont été consacrés aux entreprises qui réduisent considérablement leurs effectifs — désignées entreprises à réduction rapide des effectifs (ERR) dans la présente étude. En effet, la documentation existante sur les EFC et les gazelles ne présente pas de pendant manifeste portant sur la queue gauche (ou queue négative) de la distribution. Pourtant, la « destruction créative » décrite pour la première fois par Schumpeter (1942) met l’accent sur l’importance du processus destructeur. De jeunes entreprises novatrices lancent sans cesse des défis aux entreprises en place, qui doivent parfois réagir en ajustant considérablement leurs effectifs.

En s’appuyant sur les données du Programme d’analyse longitudinale de l’emploi (PALE) de Statistique Canada pour la période de 2000 à 2009, le présent document explore la distribution complète de la croissance annuelle de l’emploi des entreprises canadiennes. Alors que la plupart des ensembles de données offrent une couverture limitée des entreprises selon l’industrie ou la taille, les données du PALE englobent toutes les entreprises ayant des employés au Canada. Mais surtout, alors que la plupart des études portent sur la croissance totale des entreprises, y compris le transfert d’emplois à la suite de fusions et d’acquisitions, la structure du PALE permet d’isoler la création ou la destruction nette d’emplois, c’est-à-dire la croissance organique, au niveau de l’entreprise.

La présente étude montre que les distributions des taux de croissance de l’emploi des entreprises canadiennes ne sont pas gaussiennes : leur densité est plus forte au centre et dans les queues que celle de la distribution normale. Les queues plus épaisses que la normale soulèvent deux questions.

Premièrement, quelle est l’importance du rôle joué dans la croissance globale de l’emploi par les entreprises qui se trouvent dans les queues de la distribution? Même si les entreprises présentant une croissance très forte ou un déclin très rapide sont plus nombreuses que prévu, contribuent-elles de façon disproportionnée à la dynamique agrégée de l’emploi au Canada?

Deuxièmement, de nombreuses études cherchent à déterminer si les courbes de croissance moyennes dépendent de la taille et de l’âge de l’entreprise. La présente étude vise à répondre à la question de savoir si la taille et l’âge de l’entreprise ont une incidence sur les perspectives d’une croissance s’écartant de la moyenne. La taille ou l’âge influent-ils sur la propension d’une entreprise à être une EFC ou une ERR? En particulier, les grandes entreprises sont-elles plus stables que les petites? Les petites/jeunes entreprises ont-elles tendance à être davantage axées sur la croissance?

La section qui suit est consacrée à la revue des travaux empiriques sur les courbes de distribution de la croissance des entreprises, y compris les queues. La section 3 décrit la source des données et les mesures empiriques utilisées. La section 4 décrit la distribution de la croissance de l’emploi au Canada. La section 5 donne les résultats de la contribution des entreprises à forte croissance (EFC) et des entreprises à réduction rapide des effectifs (ERR) à la dynamique globale de l’emploi. La section 6 donne la description du modèle de régression quantile utilisé et la section 7, les résultats de ces régressions. La section 8 conclut le document.

2 Contexte

La présente étude s’inspire de trois corpus de publications : l’un, abondant, qui porte sur la croissance des entreprises et remonte à plus d’un demi-siècle, un deuxième, beaucoup plus restreint, qui porte sur la nature de la distribution de la croissance des entreprises et est associé principalement au domaine de recherche de l’éconophysique, et un troisième, naissant, qui porte sur les entreprises à forte croissance.

2.1 Croissance des entreprises

La documentation existante sur les déterminants de la croissance des entreprises est de trop grande portée pour en faire la chronique dans le présent document. Elle est axée en grande partie sur la validité de la loi de Gibrat — l’observation, faite en 1931 par Robert Gibrat, selon laquelle les taux de croissance prévus des entreprises sont indépendants de la taille de ces dernières. La discussion des implications théoriques de la loi de Gibrat figurant dans Sutton (1997) est celle citée le plus fréquemment. Audretsch et coll. (2004) offrent la métaétude la plus complète des travaux empiriques existants; des 59 études qu’ils énumèrent, 31 arrivent à la conclusion que la « loi de la croissance proportionnelle », comme est également appelée la loi de Gibrat, est violée d’une façon ou d’une autre.

Selon la loi de Gibrat, les entreprises subissent des chocs dont la distribution ne dépend pas de leur taille et leur capacité à réagir est proportionnelle à leur taille. Si cela est vrai, les distributions observées des taux de croissance, conditionnement à la taille, ont des moyennes et des variances identiques, et ne présentent pas de persistance.

De nombreuses études révèlent une relation négative entre la taille moyenne de l’entreprise et la croissance, ce qui contredit la loi de Gibrat. D’autres pas. Par exemple, les études récentes de Dixon et Rollin (2012) et de Haltiwanger et coll. (2010) des économies canadiennes et américaines, respectivement, montrent qu’au cours des années 2000, toute relation négative existante entre la taille et la croissance disparaît et, en fait, devient positive lorsque l’on tient compte de l’âge de l’entreprise.

La plupart des études ont montré que la variance des taux de croissance est reliée négativement à la taille, ce qui porte à croire que les petites entreprises courent un plus grand risque de déclin ou d’échec ou ont davantage de possibilités de croissance⁴. Cette constatation est intuitivement intéressante. Les petites entreprises sont considérées comme possédant des liens ténus avec les marchés financiers, ce qui amplifie les effets des chocs. En outre, les grandes entreprises détiennent habituellement un plus vaste portefeuille de produits pour amortir les chocs de la demande. Cependant, Sutton (2002) constate que la relation entre la taille de l’entreprise et la volatilité est plus plate que prévu, ce qui donne à penser que l’accès aux marchés financiers et la diversification du portefeuille offrent une certaine stabilité supplémentaire, mais que celle-ci n’est pas énorme.

Les études publiées n’abordent pas la question de savoir quelle part de la plus grande volatilité des petites entreprises est attribuable à des chocs et à des ajustements modérés, mais fréquents, et quelle part est due à des variations moins fréquentes, mais beaucoup plus importantes de l’effectif de l’entreprise. Elles supposent aussi implicitement que les distributions des taux de croissance sont symétriques, c’est-à-dire que les petites entreprises sont tout aussi susceptibles de prospérer/décliner que les grandes entreprises.

2.2 Distributions des entreprises

La plupart des études sur la croissance des entreprises ont été limitées au premier moment (moyenne) et au deuxième moment (écart-type) de la croissance. Les études de la forme globale des distributions de la croissance des entreprises sont moins fréquentes et ont été réalisées avec des données européennes par Bottazzi et Secchi, et des données américaines par les « éconophysiciens », un petit groupe de physiciens qui appliquent les outils de leur discipline aux microdonnées sur les entreprises. Ces études révèlent une distribution en forme de tente des taux de croissance de l’emploi, des ventes et des actifs pour les grandes entreprises américaines figurant dans la base des données Compustat (Amaral et coll., 1998; Stanley et coll., 1996), pour l’industrie pharmaceutique mondiale (Bottazzi et Secchi, 2005), pour le secteur italien de la fabrication (Bottazzi et coll., 2007), pour le secteur chilien de la fabrication (Halket, 2006), et pour le secteur français de la fabrication à divers niveaux de désagrégation (Bottazzi et coll., 2011). Lothian (2006) a également observé une distribution en forme de tente de la croissance annuelle des ventes des entreprises canadiennes entre 1976 et 1998.

Leur présence dans de si nombreux ensembles de données, et leur persistance à divers niveaux d’agrégation font des distributions en forme de tente un fait stylisé dont doivent tenir compte les théories de la croissance des entreprises. Certaines explications évoquent la similarité entre les distributions de la croissance des entreprises et celles de certains phénomènes observés en sciences naturelles, mais ces modèles sont difficiles à expliquer au moyen de variantes du comportement économique.

Stanley et coll. (1996) proposent un modèle dans lequel les entreprises sont composées de multiples unités, chacune croissant ou rapetissant conformément à la loi de Gibrat. À mesure qu’une unité grandit, il devient plus difficile de la gérer, de sorte qu’il est de plus en plus tentant de séparer une partie de ses ressources pour lancer une nouvelle unité, ce qui donne lieu à une forte augmentation de la taille de l’entreprise. Si cette explication paraît plausible pour les grandes entreprises sur lesquelles portent les données de ces auteurs (ils utilisent les données de Compustat qui n’englobent que les grandes entreprises américaines cotées en bourse), elle semble moins appropriée pour décrire les petites entreprises comme étant composées d’unités. Néanmoins, d’autres études révèlent les mêmes distributions pour les petites entreprises.

Coad et Planck (2012) offrent un modèle plus général, fondé sur le concept de « criticalité auto-organisée ». Les entreprises sont capables de croître grâce à l’existence d’un certain flottement organisationnel que les gestionnaires cherchent à minimiser. Des travailleurs de production supplémentaires peuvent être intégrés dans la hiérarchie d’une entreprise à condition que les superviseurs soient suffisamment nombreux pour les gérer. À certains points critiques, les ressources de supervision deviennent trop occupées et l’ajout de nouveaux travailleurs requiert l’embauche de nouveaux superviseurs, qui, à leur tour, requièrent de nouveaux gestionnaires, de nouveaux spécialistes des ressources humaines, et ainsi de suite. De petits chocs peuvent donc entraîner de grands changements de taille de l’entreprise.

Il se peut aussi que les distributions soient un artéfact des données. Selon Halket (2006), les taux de croissance semblent suivre des distributions variance-gamma (également appelées distributions de Laplace généralisées). Elles se produisent lorsque la grandeur de la variation est stochastique et suit une distribution normale, et que le moment de la variation est également aléatoire et suit une distribution gamma. Dans le cas des entreprises, Haklet suggère que l’effectif est sujet à des chocs de tailles variables, survenant à des moments qui, dans les données, semblent être aléatoires. En effet, les entreprises pourraient procéder à des changements qui ont des résultats incertains, mais conformément à un plan préétabli. Le calendrier de ces changements sera déterminé par divers détails propres aux produits vendus, aux processus technologiques utilisés et à d’autres facteurs propres à l’industrie, voire même à l’entreprise. Par contre, la collecte des données suit habituellement un calendrier fixé par le soleil : par exemple, les données sur l’emploi sont recueillies à une date calendaire particulière et sinon, sont inscrites dans un calendrier par après. L’existence d’intervalles aléatoires pourrait donc refléter une discordance entre le temps calendaire et le temps « économique ».

2.3 Entreprises dans les queues de la distribution

2.3.1 Entreprises à forte croissance

Les travaux de recherche sur les distributions ont porté principalement sur un processus de croissance qui est commun aux entreprises. Néanmoins, les auteurs d’études de plus en plus nombreuses soutiennent que les entreprises qui se trouvent dans la queue positive de la distribution — les EFC — diffèrent des autres. Les EFC joueraient un rôle d’une importance unique dans la croissance de l’économie, en tant que créatrices d’emplois et de moteur de l’innovation. La notion populaire est que les EFC sont de jeunes entreprises du secteur de la haute technologie qui apportent des technologies révolutionnaires à l’économie.

Cependant, les études publiées au sujet des EFC n’ont pas créé une base de preuves cumulatives, en grande partie parce qu’elles ne s’appuient pas sur les mêmes ensembles de données, indicateurs de croissance et définitions de la forte croissance. Il s’en est suivi une confusion quant à la nature et à la signification du processus de forte croissance. Une des interprétations de cette confusion est que la croissance des entreprises en général, et la forte croissance en particulier, est un phénomène hétérogène caractérisé par divers types d’entreprises suivant des chemins de croissance différents.

Comme « toutes les entreprises à forte croissance ne croissent pas de la même façon », Delmar et coll. (2003) soutiennent que des études fondées sur des mesures uniques de la croissance ne renseigneront que sur un seul type de croissance organisationnelle. Les études de la croissance des ventes ou des actifs pourraient ne pas brosser le même tableau du processus que les études de l’emploi. Les études sur la croissance totale, incluant les fusions et les acquisitions, pourraient désigner comme des EFC d’autres entreprises que celles repérées au moyen d’études portant sur la croissance organique uniquement, et ce avec des implications fort différentes. D’aucuns ont aussi soutenu que les variations absolues peuvent ne pas peindre le même tableau que les mesures relatives.

La plupart des études portent sur une seule mesure de la croissance. Delmar et coll. (2003, p. 194) constatent « l’émergence d’un consensus selon lequel, si un seul indicateur doit être choisi comme mesure de la croissance des entreprises, la mesure privilégiée devrait être celle des ventes » [Traduction]. Cependant, la majorité des études sur les EFC se sont concentrées sur l’emploi. Cela pourrait tenir simplement au fait que les premiers chercheurs étaient préoccupés par le phénomène de création d’emplois. Toutefois, si les entreprises sont considérées comme des ensembles de ressources, l’emploi pourrait être une meilleure mesure de leur taille et de leur complexité que la valeur de leurs produits⁵.

Henrekson et Johansson (2010) présentent une revue à grande échelle des études sur les EFC en tant que créatrices d’emplois. Ils examinent trois propositions quant à la nature des EFC : 1) elles sont surreprésentées dans les industries de la haute technologie; 2) elles sont plus jeunes que les autres entreprises; et 3) elles sont plus petites que les autres entreprises. Henrekson et Johansson concluent que les EFC se retrouvent dans toutes les industries et non pas simplement dans le secteur de la haute technologie, et bien qu’elles soient relativement jeunes et petites, elles ne sont pas toutes des entreprises en démarrage. En fait, elles pourraient ne pas être nécessairement si jeunes; Acs et coll. (2008) constatent que l’âge moyen des entreprises ayant une forte incidence est de 25 ans⁶. En outre, la contribution des grandes EFC à la création d’emplois est importante en valeur absolue.

Henrekson et Johansson (2010) constatent qu’il existe un problème de définition des EFC, et les études qu’ils citent s’appuient sur des définitions différentes. La définition correspondant à une croissance annualisée moyenne de 20 % sur trois années consécutives donnée par l’Eurostat et l’Organisation de coopération et de développement économiques (Eurostat et OCDE, 2007)⁷ est la plus fréquente, mais d’autres seuils et périodes de référence sont utilisés. Certains chercheurs examinent la fraction supérieure d’entreprises selon la croissance, comme les 5 % ou 10 % d’entreprises ayant la croissance la plus rapide. Les deux définitions sont arbitraires.

Les études diffèrent aussi selon que la croissance des EFC est « organique » (ajout de nouveaux emplois) ou comprend aussi les fusions et les acquisitions (prise d’emplois existants provenant d’autres entreprises). Les entreprises dont la croissance est organique ajoutent des emplois par la voie du marché du travail, ou des ventes en faisant directement des démarches auprès de nouveaux clients. En revanche, les entreprises dont la croissance se fait par acquisition ajoutent de nouveaux employés ou clients en fusionnant avec d’autres d’entreprises ou en acquérant d’autres entreprises. En raison des limites des données, la plupart des travaux de recherche sur les EFC ont porté sur la croissance totale, qui englobe la croissance organique et par acquisition.

Dans la perspective de l’entreprise, la croissance organique et la croissance par acquisition mènent toutes deux à une expansion des ressources qui doit être gérée. Par contre, dans la perspective sociale, la croissance organique et la croissance par acquisition ont des conséquences différentes. Si l’objectif social est d’accroître le nombre d’emplois, les études devraient se concentrer uniquement sur la croissance organique. La croissance par acquisition, en soi, ne donne pas lieu à une création nette d’emplois, mais plutôt au transfert d’emplois existants d’une entreprise dans une autre. En outre, les deux types de croissances pourraient être en contradiction sur le plan de la signification sociale. Selon McKelvie et Wiklund (2010), les EFC qui recourent à l’acquisition sont souvent des agents de destruction organique d’emplois.

Certaines données font penser que le mode de croissance diffère systématiquement selon le type d’entreprises. Des études menées en Suède (Delmar et coll., 2003) et en Finlande (Deschryvere, 2008) révèlent que la croissance des entreprises jeunes et petites a tendance à être organique, tandis que celle des entreprises plus grandes et plus âgées est plus susceptible de se faire par acquisition. Delmar et ses collaborateurs (2003, p. 210) concluent que, « par rapport aux études antérieures, ces résultats appuient largement la notion voulant que la croissance organique soit davantage associée aux entreprises jeunes et petites et que la croissance par acquisition soit plus fréquente chez les entreprises plus grandes et plus anciennes, et chez les entreprises appartenant à des secteurs en stagnation ou à faible technologie » [Traduction].

La plupart des études s’appuient sur la croissance relative (en pourcentage), quoique certaines utilisent la croissance absolue ou une combinaison des deux mesures. Comme la plupart des études de la croissance des entreprises ont pour point de départ la loi de Gibrat, la croissance relative a tendance à être plus répandue, quoique certains auteurs soutiennent que la croissance absolue convient mieux pour répondre à la question « Qui crée les emplois? » Dans le contexte des EFC, les auteurs de certaines études mettent en garde contre le fait que, parce qu’il est plus facile pour les petites entreprises d’atteindre des taux de croissance très élevés, même si elles n’ajoutent que quelques employés, les mesures relatives pourraient induire en erreur.

Le présent article porte exclusivement sur la croissance organique d’une année à l’autre. Il est également axé sur la croissance relative, qui est souvent soupçonnée de donner l’avantage aux petites entreprises en ce qui concerne le classement dans la catégorie à « forte croissance ». Cependant, les résultats présentés à la section 7 portent à croire que ce « problème du faible effectif de base » ne constitue peut-être pas une question importante. Dans la présente étude, aucun critère arbitraire n’est établi pour identifier les EFC.

2.3.2 Entreprises à réduction rapide des effectifs

Des études ont été consacrées aux déterminants de la disparition, ou de manière équivalente, de la survie des entreprises, mais le même type d’analyse n’a pas été appliqué aux entreprises qui réduisent sévèrement leurs effectifs. Selon diverses études, le jeune âge et la petite taille augmentent la probabilité qu’une entreprise ferme ses portes (Geroski, 1995; Evans, 1987; Baldwin, 1995; Mata et Portugal, 1994; Esteve Perez et coll., 2004).

Quels sont les facteurs qui contribuent à une réduction prononcée des effectifs? À l’heure actuelle, la documentation spécialisée ne permet pas de répondre à cette question, quoique quelques études aient porté sur les profils de croissance durant les années qui ont précédé la fermeture (Troske, 1996; Huynh et Petrunia, 2012). Alors que certaines entreprises qui rapetissent obtiennent de mauvais résultats avant de fermer leurs portes, d’autres demeurent concurrentielles en réduisant radicalement leurs effectifs. Il se pourrait que les petites et/ou les jeunes entreprises réduisent rapidement leur personnel en réaction à des chocs négatifs, parce que leurs ressources financières sont limitées. Par ailleurs, les témoignages d’entreprises bien établies qui ont atteint la maturité et qui mettent à pied un grand nombre d’employés dans le cadre d’une stratégie de restructuration sont fréquents.

L’étude simultanée des queues droite et gauche de la distribution de la croissance, comme elle est faite dans la présente étude, permet de mieux définir la nature du processus concurrentiel.

3 Données et mesures

3.1 Source des données

La présente analyse porte sur des renseignements tirés du programme d’analyse longitudinale de l’emploi (PALE) de Statistique Canada⁸, une base de données administratives englobant toutes les entreprises de l’économie canadienne qui ont une certaine masse salariale et qui, par conséquent, émettent au moins un « État de la rémunération payée » (feuillet T4). Le PALE englobe les entreprises constituées et non constituées en société, sauf les entreprises individuelles (travailleurs autonomes) et les sociétés de personnes dont les associés ne touchent pas de salaire. Il s’agit d’un fichier longitudinal qui permet de suivre le niveau d’emploi annuel des entreprises au cours du temps⁹.

Le fichier du PALE ne couvre que la croissance organique. Les « fausses » créations et disparitions d’entreprises qui peuvent découler d’une restructuration d’entreprises (par exemple, fusions et acquisitions, entreprises dérivées et dessaisissements) sont supprimées. Ces transactions représentent des emplois qui changent d’entreprise plutôt que la création de nouveaux emplois ou la destruction d’emplois existants, qui constituent le processus examiné ici.

Les fausses créations et disparitions d’entreprises sont supprimées en procédant à un « suivi de la main-d’œuvre ». Les groupes d’employés d’entreprises qui apparaissent et disparaissent sont comparés aux groupes d’employés d’autres entreprises durant l’année précédente (pour les entreprises qui apparaissent) ou l’année suivante (pour les entreprises qui disparaissent). Si l’on constate qu’une proportion importante d’employés faisait partie auparavant ou fait partie subséquemment de l’effectif d’une autre entreprise, on établit un lien entre les deux entreprises concernées et la structure de l’entreprise à l’année $t$ est appliquée aux données des deux entreprises à l’année $t - 1$ et toutes les années antérieures.

De nouvelles versions de la base de données du PALE sont produites périodiquement. Lorsque des données deviennent disponibles pour une année supplémentaire, on crée un nouveau fichier longitudinal, ou nouvelle version. La version 2009 du PALE fait le suivi de l’emploi dans les entreprises de 1983 à 2009; la version 2008 fait le suivi de l’emploi de 1983 à 2008, et ainsi de suite. Dans chaque version, on s’appuie sur l’information concernant l’année la plus récente pour laquelle des données sont disponibles. Par exemple, dans la version 2009 du PALE, les données annuelles antérieures sont agrégées en se basant sur la structure de l’entreprise en 2009; dans la version 2008, les données antérieures sont agrégées en se basant sur la structure de 2008. Donc, deux entreprises qui fusionnent en 2009 sont considérées comme une entreprise unique de 1983 à 2009 dans la version 2009 de la base des données, mais sont enregistrées comme des entreprises distinctes de 1983 à 2008 dans la version 2008.

Ce mode de traitement a pour avantage de faire presque entièrement abstraction du fait que des entreprises changent de main, et d’enregistrer seulement la « croissance organique » due à l’ajout de nouvelles entreprises ou de nouveaux employés aux entreprises existantes. La base de données du PALE permet donc d’isoler l’activité des entreprises qui modifie la demande en main-d’œuvre dans l’économie.

Cependant, le fait que, dans chaque version, la structure du marché de la dernière année est appliquée rétroactivement aux années antérieures crée une difficulté supplémentaire. Pour chaque version, appliquer rétroactivement la structure courante au-delà de l’année $t - 1$ risque d’entraîner des erreurs de classification des sources de croissance pour chaque année, sauf les deux dernières. Ainsi, dans la version 2007, la structure d’une entreprise qui a participé à une activité de fusion et acquisition en 2008 diffère clairement de sa structure dans la version 2009. L’entreprise fusionnée, telle qu’elle qu’existe à l’année $t$ , ne peut pas être considérée comme responsable des opérations consolidées à l’année $t - 2$ des entreprises distinctes à partir desquelles elle a été formée.

Afin de résoudre le problème d’erreur de classification durant les années antérieures pour chaque version du PALE, la présente étude porte uniquement sur les données provenant des deux dernières années de chaque version du fichier PALE de 2000 à 2009. Il en résulte une série de dix échantillons transversaux qui sont regroupés pour étudier la distribution des taux de croissance. Par conséquent, les comparaisons portent sur des périodes d’un an seulement et la structure des entreprises est maintenue constante pendant la deuxième année de chaque échantillon transversal.

La portée de l’étude est limitée au secteur des entreprises. On a donc exclu des échantillons transversaux les entreprises classées dans les secteurs 91 (administrations publiques), 61 (services d’enseignement) et 62 (soins de santé et assistance sociale) du Système de classification des industries de l’Amérique du Nord (SCIAN)¹⁰.

3.2 Mesure de l’effectif et de l’âge des entreprises

La base de données PALE contient des renseignements annuels sur la masse salariale (masse salariale totale et nombre total d’employés qui ont reçu un feuillet T4 au cours de l’année civile). Sur la base de ces données, on infère l’effectif de l’entreprise au moyen d’une mesure appelée unité moyenne de main-d’œuvre (UMM)¹¹.

L’UMM est une mesure obtenue en divisant la masse salariale annuelle de chaque entreprise par les gains annuels moyens d’un travailleur représentatif dans les mêmes industrie, province et catégorie de taille d’entreprise, déterminés en utilisant des données provenant de l’Enquête sur l’emploi, la rémunération et les heures de travail réalisée mensuellement par Statistique Canada¹². Pour une description du calcul du nombre d’UMM, voir Lafrance et Leung (2010).

Le nombre d’UMM est une mesure indirecte de l’effectif. Il peut varier en fonction de deux dimensions — le nombre de travailleurs et leur rémunération moyenne. Cette dernière varie d’une entreprise à l’autre en raison de la durée de l’emploi au cours d’une année, du nombre d’heures travaillées et du salaire versé. Les entreprises dont le nombre d’UMM est faible peuvent avoir peu d’employés et celles dont le nombre est plus élevé, en avoir un plus grand nombre, mais les entreprises peuvent aussi avoir un grand nombre d’UMM parce qu’elles payent des salaires supérieurs à la moyenne de l’industrie ou un petit nombre, parce qu’elles payent moins que la moyenne. Par conséquent, la mesure fondée sur le nombre d’UMM tient compte de la qualité de l’emploi évaluée d’après la rémunération.

Lorsque des entreprises ne sont en activité que pendant une partie de l’année, leur effectif est sous-estimé par la mesure du nombre d’UMM. Cette sous-estimation est plus importante pour les entreprises en démarrage créées à la fin de l’année civile et pour les entreprises sortantes qui ferment leurs portes durant les premiers mois de l’année. La sous-estimation de la taille des entreprises entrantes et sortantes a des répercussions sur les taux de croissance durant l’année qui suit l’entrée et durant celle qui précède la sortie. Les taux de croissance des entreprises en démarrage qui survivent jusqu’à l’année suivante sont surestimés, et les taux de croissance dans l’intervalle entre l’année qui précède la sortie et l’année de la sortie paraissent plus négatifs qu’ils ne le sont réellement. À cause de cette limite des données, seules les entreprises en place âgées d’au moins deux ans sont incluses dans la présente analyse¹³.

L’âge de l’entreprise est attribué à chaque enregistrement transversal en utilisant la méthode décrite dans Dixon et Rollin (2012).

3.3 Définition de la taille de l’entreprise et du taux de croissance

La méthode classique de l’« année moyenne » décrite par Davis et coll. (1996) est utilisée pour calculer la taille de l’entreprise et le taux de croissance pour chaque observation transversale $i$ . La taille de l’entreprise, désignée par $X_{i t}$ , est la taille moyenne de l’entreprise aux années $t - 1$ et $t$ . Cela s’écrit :

$X_{i t} = \frac{E_{i t} + E_{i t - 1}}{2}$

Le taux de croissance de l’observation transversale $i$ de l’année $t - 1$ à l’année $t$ est défini comme étant :

$g_{i t} = \frac{E_{i t} - E_{i t - 1}}{X_{i t}}$

où $E_{i t}$ est l'effectif de l'entreprise durant l'année $t$ , et $E_{i t - 1}$ , son effectif durant l'année $t - 1$ .

Cette formulation améliore les effets de la régression à court terme vers la moyenne, c’est-à-dire la tendance des entreprises en croissance (déclin) à revenir vers le niveau d’emploi moyen à la période suivante par réduction (accroissement) de leur effectif.

Le taux de croissance utilisé donne des résultats similaires au logarithme des taux de croissance, du moins pour les entreprises dont l’effectif s’accroît ou se contracte dans une proportion allant jusqu’à 50 % (selon des mesures logarithmiques moyennes). La principale différence par rapport à la croissance logarithmique est que le taux de croissance « annuel moyen » est linéaire et borné entre -2 (sortie) et 2 (entrée) aux deux extrémités. Par conséquent, les entrées et les sorties d’entreprises représentent un sous-ensemble distinct qui n’est pas directement comparable aux autres observations. En outre, la taille attribuée à ces observations transversales correspond, par construction, à la moitié de la taille réelle de l’entreprise au moment de son entrée ou de sa sortie. En raison du traitement arbitraire de l’entrée et de la sortie des entreprises, la présente analyse se concentre sur les entreprises demeurées en exploitation, qui représentent la base des entreprises en activité pendant deux années consécutives.

Les entreprises en place pour lesquelles la taille $X_{i t}$ est inférieure à une UMM sont également exclues, à cause du problème du faible effectif de base. Le cas échéant, des variations infinitésimales de l’effectif peuvent entraîner des taux de croissance très élevés ou très faibles.

4 Distribution des taux de croissance de l’emploi au Canada

4.1 Distribution globale

Comme il est discuté à la sous-section 2.2, les distributions des taux de croissance des entreprises observées dans divers pays ne sont pas gaussiennes, leur densité étant plus forte au centre et dans les queues. Afin d’illustrer la distribution des taux de croissance de l’emploi des entreprises canadiennes, des histogrammes sont construits en créant des classes de taux de croissance d’une largeur de 0,05, ou environ 5 % (log), et en calculant la part d’observations comprise dans chaque classe. La largeur des classes a été choisie de manière à préserver la confidentialité des renseignements fournis par les entreprises et à simplifier l’exposé.

La distribution des taux de croissance de l’emploi des entreprises en place ne variait que légèrement au cours de la période de 10 ans étudiée, même si celle‑ci comprenait la récession économique de 2008-2009 (graphique 9 en annexe). Le regroupement des observations pour ces années est, par conséquent, la méthode adoptée dans la suite du document.

La distribution empirique diffère considérablement d’une distribution normale (graphique 1). Il s’agit d’une distribution leptokurtique, qui est plus pointue au centre et possède des queues plus épaisses.

Graphique 1

Description pour graphique 1

La tendance centrale de la distribution, mesurée par la moyenne et la médiane, est proche de zéro (voir l’encadré plus bas). Ce fait, ainsi que la forte concentration de la densité autour du centre, implique que l’effectif de la plupart des entreprises varie peu d’une année à l’autre. La moitié des entreprises — celles comprises entre les 25e et 75e centiles — modifient leur effectif de moins de 15 % de chaque côté.

Tableau
Statistiques sommaires pour la distribution des taux de croissance de l’emploi, Canada, 2000 à 2009
Nombre d’observations :	5,3 millions
Moyenne :	-0,02
Écart-type :	0,40
Asymétrie :	-0,75
Kurtosis :	4,86
10e centile :	-0,43
25e centile :	-0,15
Médiane :	0,00
75e centile :	0,15
90e centile :	0,36
Intervalle interquartile :	0,30
Intervalle entre déciles :	0,78

Des quelque demi-million d’entreprises qui contribuent à la création d’emplois chaque année, les entreprises établies (deux ans ou plus et au moins une UMM) sont à l’origine des deux tiers des nouveaux emplois. Du côté de la destruction de l’emploi, les entreprises établies représentent plus des trois quarts des pertes d’emplois. Par conséquent, la majeure partie de la dynamique de l’emploi se déroule au sein des entreprises établies.

La distribution est étalée vers la gauche. Cette asymétrie négative se manifeste par une statistique d’asymétrie de -0,75, et par le fait que la moyenne (-0,02) est inférieure à la médiane (0,00). Donc, la moyenne est influencée par la densité dans la queue gauche, qui est plus épaisse que la queue droite.

Le kurtosis, qui mesure l’aplatissement et l’épaisseur des queues d’une distribution, est égal à 4,86. Cette valeur est supérieure à celle de la distribution normale (3,0), mais inférieure à celle de la distribution de Laplace (6,0). L’exécution d’un test de normalité d’Agostino-Pearson a donné lieu au rejet de l’hypothèse nulle d’une distribution gaussienne, tant sur la base de l’asymétrie que du kurtosis excédentaire.

Ensemble, ces données brossent un tableau de la dynamique de la croissance des entreprises où un grand nombre d’entreprises changent peu d’une année à l’autre, tandis qu’un petit nombre s’accroissent ou déclinent appréciablement.

Les formes des distributions ne correspondent pas à celles que l’on attendrait d’une croissance des entreprises consistant en un grand nombre d’innovations dont les distributions sont indépendantes¹⁴. Elles ressemblent plutôt à des distributions de Laplace généralisées, qui sont parfois utilisées en finance pour l’évaluation des options. On sait que les prix des options sont caractérisés par des sauts ou des pics fréquents qui sont difficiles à modéliser en utilisant des variables aléatoires normales indépendantes et identiquement distribuées. Le fait que la croissance des entreprises suive des distributions similaires porte à croire que les entreprises peuvent aussi évoluer de façon discontinue, plutôt qu’en douceur¹⁵.

4.2 Distributions conditionnelles

4.2.1 Industrie

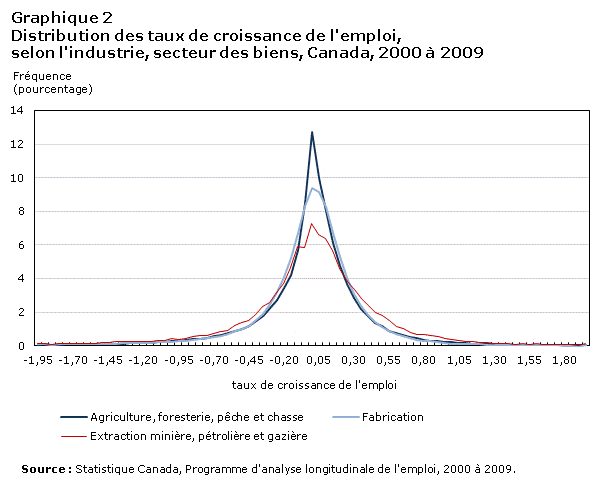
Les graphiques 2 et 3 représentent les distributions de la croissance des entreprises conditionnellement à l’industrie. Comme il est mentionné dans l’introduction, le point de vue généralement reconnu est que les EFC sont concentrées dans les industries de la haute technologie. Si cette notion est correcte, les distributions pour les catégories d’industries contenant les industries de la haute technologie (en particulier la fabrication) devraient posséder des queues plus épaisses que celles observées pour les autres industries.

En fait, l’épaisseur des queues, dans lesquelles sont situées les entreprises susceptibles d’être des EFC et des ERR, est une caractéristique commune à toutes les industries. Autrement dit, même si la croissance rapide et le déclin rapide sont généralement associés à l’industrie de la haute technologie, les résultats observés pour la plupart des autres industries présentent la même distribution de type Laplace. Cette constatation est en harmonie avec les travaux sur la croissance rapide, selon laquelle les EFC sont présentes dans diverses industries (Henrekson et Johansson, 2010).

Graphique 2

Description pour graphique 2

Graphique 3

Description pour graphique 3

4.2.2 Taille et âge

La plupart des travaux sur la dynamique des entreprises sont axés sur la relation entre la taille et la croissance, en tenant compte parfois de l’âge de l’entreprise. Comme il est mentionné à la section 2, les résultats publiés sont ambivalents en ce qui a trait à la vérification de la loi de Gibrat pour les moyennes, mais indiquent systématiquement que la variance des taux de croissance est plus grande pour les petites entreprises.

Les résultats de la présente analyse font penser que les différences dans les moyennes et dans les variances conditionnelles selon la taille de l’entreprise ne sont pas dictées par la masse d’entreprises au centre de la distribution, mais par les entreprises situées dans les queues. En particulier, les queues de la distribution sont plus épaisses pour les classes de petites entreprises, surtout pour celles comptant moins de 10 employés (graphique 4). Cependant, l’influence de la taille semble être asymétrique, la queue négative s’épaississant plus rapidement que la queue positive à mesure que diminue la taille de l’entreprise.

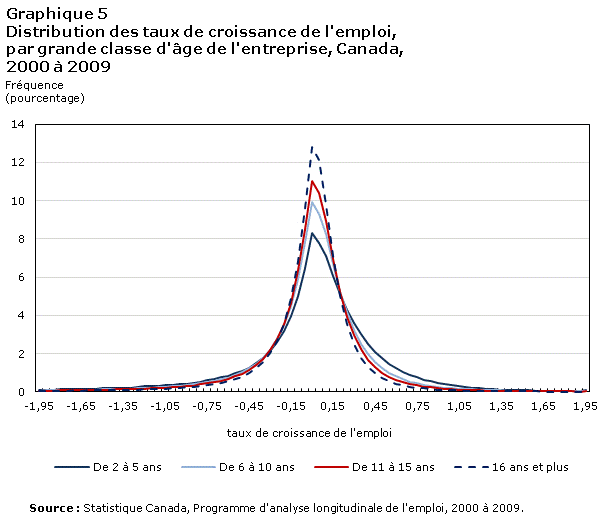
Les distributions de la croissance des jeunes entreprises possèdent des queues plus épaisses que celles de la croissance des entreprises plus anciennes (graphique 5). Toutefois, les distributions selon l’âge présentent l’asymétrie opposée à celle observée dans le cas des distributions selon la taille. La queue positive est particulièrement épaisse pour les jeunes entreprises¹⁶. L’asymétrie positive de ces distributions suggère que, contrairement à leurs homologues plus âgées, les jeunes entreprises ont tendance à avoir une croissance rapide ou ont déjà disparu (auquel cas elles ne figurent pas dans les données).

Ces résultats soulèvent un certain nombre de questions. Premièrement, la nature non gaussienne des distributions des taux de croissance des entreprises mérite une explication, mais celle-ci sera reportée à de futures études. Deuxièmement, dans quelle mesure les entreprises situées dans les queues de la distribution contribuent-elles à la dynamique globale de l’emploi? La section 5 est consacrée à l’étude de leur contribution à la dynamique agrégée de l’emploi.

Troisièmement, bien que la plupart des travaux sur la dynamique des entreprises portent sur la croissance prévue des entreprises en fonction de leurs caractéristiques, comme la taille et l’âge, les différences entre les divers types d’entreprises sont plus prononcées dans l’une des queues de la distribution ou dans les deux. À la section 6, on examine comment la forme des distributions varie selon la taille et l’âge de l’entreprise, en faisant appel à des méthodes de régression quantile.

Graphique 4

Description pour graphique 4

Graphique 5

Description pour graphique 5

5 Contributions des entreprises à forte croissance et des entreprises à réduction rapide des effectifs

Les résultats de la section précédente montrent que l’effectif de la plupart des entreprises qui demeurent en activité ne varie que légèrement, mais que celui du petit nombre d’EFC et d’ERR fluctue considérablement. Mais quelles sont les entreprises à l’origine de la majeure partie de la dynamique de l’emploi — le grand nombre d’entreprises effectuant de petits changements ou le petit nombre procédant à de grands changements?

Environ un million d’employeurs sont en activité chaque année dans le secteur canadien des entreprises. Les figures 1 et 2 donnent les contributions des différents types d’entreprises à la création ou à la destruction brute d’emplois. Les tableaux font la distinction entre les entreprises en place et les entreprises entrantes ou sortantes. Une catégorie distincte regroupe les entreprises en place âgées d’un an ou dont l’effectif est inférieur à une UMM. Cette catégorie soulève certaines préoccupations. La croissance de l’emploi des entreprises âgées d’un an est vraisemblablement surestimée en raison de la méthodologie des UMM. La plupart des entreprises ne sont en activité que pendant une partie seulement de l’année de leur entrée sur le marché, ce qui donne lieu à une sous-estimation de la taille de l’entreprise, selon la date d’entrée. Les microentreprises (moins d’une UMM) souffrent du problème du petit effectif de base qui a tendance à gonfler leur taux de croissance.

Figure 1 Contribution moyenne (de 2000 à 2009) à la création brute d'emplois, selon le type d'entreprise, Canada. (La note descriptive suit.)

Note : La figure 1 montre que trois groupes d’entreprises contribuent à la création brute d’emplois. La contribution des entreprises entrantes est de 19 %. La contribution des entreprises âgées d’un an ou dont la taille est inférieure à une UMM est de 13 %. Enfin, la contribution des entreprises âgées de deux ans et plus et dont la taille est égale ou supérieure à une UMM est de 68 %. Les entreprises à forte croissance (EFC) étudiées dans la présente analyse appartiennent au troisième groupe d’entreprises, qui sont également appelées entreprises établies et en croissance. Lorsque les EFC sont définies comme ayant un taux de croissance égal ou supérieur à 20 %, ce qui est le cas pour les entreprises établies et en croissance dont les taux de croissance se situent dans les 18 % supérieurs, elles sont à l’origine de 47 % de la création brute totale d’emplois. Lorsque les EFC sont définies comme étant les entreprises établies et en croissance dont les taux de croissance correspondent aux 10 % supérieurs, le taux de croissance seuil est de 35 % et le groupe représente 38 % de la création brute totale d’emplois.

Source : Statistique Canada, Programme d’analyse longitudinale de l’emploi, 2000 à 2009.

Figure 2 Contribution moyenne (de 2000 à 2009) à la destruction brute d'emplois, selon le type d'entreprise, Canada. (La note descriptive suit.)

Note : La figure 2 montre que trois groupes d’entreprises contribuent à la destruction brute d’emplois. La contribution des entreprises sortantes est de 18 %. La contribution des entreprises âgées d’un an ou de taille inférieure à une UMM est de 4 %. Enfin, la contribution des entreprises établies âgées de deux ans et plus et de taille égale ou supérieure à une UMM est de 78 %. Les entreprises à réduction rapide des effectifs (ERR) étudiées dans la présente analyse appartiennent au troisième groupe d’entreprises, qui sont également appelées entreprises établies et en déclin. Lorsque les ERR sont définies comme ayant un taux de réduction des effectifs de 20 % ou moins, ce qui est le cas pour les entreprises établies et en déclin dont les taux de croissance se situent dans les 23 % inférieurs, elles sont à l’origine de 58 % de la destruction brute totale d’emplois. Lorsque les ERR sont définies comme étant des entreprises établies et en déclin dont les taux de croissance appartiennent aux 10 % inférieurs, le taux de réduction annuel seuil de 45 % et le groupe explique 35 % de la destruction brute totale d’emplois.

Source : Statistique Canada, Programme d’analyse longitudinale de l’emploi, 2000 à 2009.

Cependant, dans cette catégorie, la plupart des variations de l’emploi sont attribuables aux entreprises qui croissent ou qui déclinent le plus rapidement. Les EFC et les ERR peuvent être définies de deux façons : en utilisant un seuil quantile ou un seuil de taux de croissance. Si les EFC sont définies comme des entreprises, ayant un taux de croissance annuel de 20 % ou plus (ce qui en fait des candidates à la désignation d’EFC selon la définition de l’OCDE correspondant à une croissance annualisée moyenne de 20 % sur trois ans), elles ne représentent que 18 % des entreprises établies et en croissance, mais sont à l’origine de près de la moitié des emplois créés. Les entreprises à forte croissance appartenant aux 10 % supérieurs de la distribution, c’est-à-dire les entreprises situées au-delà du 90e centile (taux de croissance de 35 %), représentent près de 40 % de la création globale d’emplois.

La contribution des ERR à la destruction de l’emploi est également disproportionnée. Si l’on applique un seuil de taux de déclin de 20 %, qui concorde avec la définition de l’OCDE, 58 % de la destruction d’emplois est expliquée par les 23 % d’entreprises en déclin situées au bas de la distribution. Les 10 % d’entreprises en déclin situées au bas de la distribution, c’est-à-dire celles qui réduisent leur effectif au taux minimal de 45 % par année, sont à l’origine d’un tiers de la destruction annuelle d’emplois.

Peu importe la façon dont les EFC et les ERR sont définies, les entreprises situées dans les queues de la distribution des taux de croissance sont manifestement des déterminants importants de la dynamique de l’emploi au Canada. Quelles caractéristiques des entreprises seront les meilleurs prédicteurs d’une forte croissance ou d’un déclin rapide?

6 Cadre de la régression quantile

Aux sections qui précèdent, on a montré que les distributions des taux de croissance des entreprises ne sont pas conformes aux hypothèses des modèles de régression classiques. En outre, les résultats donnent à penser que l’étude des entreprises situées dans les queues plutôt qu’au centre de la distribution de la croissance est la clé de la compréhension de la dynamique de l’emploi au Canada.

Ces constatations soulèvent des problèmes si l’on veut appliquer les méthodes statistiques classiques. L’asymétrie et les queues lourdes des distributions signifient que les estimations classiques de la relation entre la croissance et les caractéristiques de l’entreprise, comme la taille et l’âge, doivent être interprétées avec prudence. Des valeurs aberrantes peuvent fausser les estimations des moyennes conditionnelles, et le kurtosis affecte les erreurs-types utilisées pour l’inférence. Dans la mesure où existent des variations systématiques des moments d’ordre plus élevé entre différentes entreprises, les conclusions au sujet des tendances moyennes seront faussées.

En outre, les méthodes classiques sont axées sur les tendances centrales et conviennent donc mal pour intégrer l’information recueillie à d’autres points de la distribution, nommément, dans les queues. Dans les études des EFC, ce problème est habituellement résolu en définissant un seuil de croissance arbitraire, puis en analysant les caractéristiques moyennes des entreprises qui le dépassent.

Dans le présent document, la préférence a été accordée à la régression quantile. Cette technique a l’avantage d’être non paramétrique, de sorte que l’inférence n’est pas influencée par la forme de la distribution sous-jacente. En outre, la régression quantile permet d’examiner la relation entre les caractéristiques de l’entreprise et, disons, la forte croissance, directement sans s’appuyer sur des seuils arbitraires.

Dans la plupart des études publiées sur la dynamique de l’emploi des entreprises, les variables explicatives utilisées sont la taille et l’âge de l’entreprise, et la question posée est celle de savoir si la croissance des petites entreprises est plus rapide que celle des grandes, après avoir neutralisé l’effet d’autres facteurs. La présente étude vise à répondre à la question de savoir si les petites (grandes) entreprises sont plus susceptibles d’avoir une forte croissance ou plus sujettes à réduire rapidement leurs effectifs, et si la relation avec la forte croissance (le déclin rapide) est influencée par l’âge de l’entreprise.

Pour estimer la relation statistique entre les taux de croissance, d’une part, et l’âge et la taille des entreprises, d’autre part, on utilise le modèle de régression suivant :

$g_{i t}^{θ} = α^{θ} + Z Γ^{θ} + \sum_{s = 1}^{S - 1} β_{s}^{θ} \cdot 1 \cdot {i \in s} + δ_{1}^{θ} \cdot â g e i n v_{i t} + δ_{2}^{θ} \cdot â g e i n v_{i t}^{2}_{} + υ_{i t}^{θ}$

où l’indice supérieur $0 < θ < 1$ signifie que le coefficient est évalué au quantile $θ$ . L’indice $s = 1, ..., S$ indique la classe de taille, et $1 [\cdot]$ est une fonction indicatrice qui est égale à 1 si l’entreprise $i = 1, ..., N$ appartient à la classe de taille donnée au temps $t$ . La variable de comptage $â g e i n v$ est définie comme étant égale à 17 moins l’âge de l’entreprise, et est égale à 0 pour les entreprises âgées de 17 ans et plus¹⁷^,¹⁸. Le vecteur $Z$ contient les variables de contrôle (variables nominales pour l’année et l’industrie).

Les catégories omises pour les variables nominales sont une classe de taille moyenne (de 20 à moins de 50 UMM), l’année 2003 et le secteur de la fabrication (SCIAN 31 à 33). Définir $â g e i n v$ comme étant le nombre d’années de moins que la catégorie des 17 ans et plus équivaut à exclure la catégorie la plus âgée.

Les estimations ont été calculées pour un quantile sur cinq, ce qui donne un total de 19 estimations ( $θ$ = 0,05, 0,10, ..., 0,95). Les intervalles de confiance ont été calculés en utilisant les erreurs-types obtenues par une méthode bootstrap pour chaînes de Markov (en effectuant 200 itérations. Pour des renseignements détaillés sur les mécanismes de la régression quantile, voir Koenker (2005) ou Hao et Naiman (2007).

Dans le cas de la régression linéaire, l’ordonnée à l’origine correspond au taux de croissance moyen des catégories omises, et les coefficients des variables nominales donnent la variation de la moyenne qui résulte du changement de catégorie, tous les autres facteurs étant maintenus constants. Dans la régression quantile, l’ordonnée à l’origine correspond au taux de croissance des entreprises définies par les catégories omises (entreprises comptant au moins 20 UMM, mais moins de 50, et âgées de 17 ans et plus) à un point de la distribution spécifiée par $θ$ . Les coefficients $β_{s}^{θ}$ représentent les différences de taux de croissance au centile $θ$ entre le groupe de référence et les entreprises incluses dans la classe de taille $s$ , après neutralisation de l’effet de l’âge et d’autres caractéristiques. Les coefficients $δ_{1}^{θ}$ et $δ_{2}^{θ}$ peuvent être utilisés pour calculer l’effet marginal d’un rajeunissement (vieillissement) d’un an sur la croissance des entreprises au quantile $θ$ , en neutralisant l’effet de la taille et d’autres caractéristiques.

7 Résultats des régressions quantiles

Les entreprises qui connaissent une forte croissance ou qui réduisent rapidement leurs effectifs sont une caractéristique dominante des données, et contribuent quantitativement de manière importante à la dynamique agrégée de la croissance. Mais quels sont les types d’entreprises les plus susceptibles d’avoir une forte croissance ou de réduire rapidement leur effectif? Les principaux résultats des régressions, présentés aux graphiques 6 à 8, portent sur deux caractéristiques, à savoir la taille et l’âge de l’entreprise.

Les graphiques 6 et 7 représentent les coefficients de classe de taille $β_{s}^{θ}$ pour les entreprises plus petites et plus grandes que le groupe de référence (entreprises comptant de 20 à moins de 50 UMM), respectivement. Les taux de croissance pour le groupe de référence sont normalisés à zéro et s’alignent donc sur l’axe horizontal. Le graphique 10 en annexe montre les taux de croissance du groupe de référence.

Les courbes des graphiques 6 et 7 montrent dans quelle mesure la croissance d’une classe de taille donnée est plus rapide (valeurs situées au-dessus de l’axe horizontal) ou plus lente (valeur située en dessous de l’axe horizontal) que celle du groupe de référence dans chaque quantile. Les courbes à pente positive (négative) signifient que la classe de taille présente une plus (moins) grande dispersion que le groupe de référence, c’est-à-dire des taux de croissance plus (moins) négatifs dans la queue gauche et des taux de croissance plus (moins) positifs dans la queue droite.

L’asymétrie se manifeste par une différence de distance par rapport à l’axe horizontal entre les côtés gauche et droit de la médiane. Une asymétrie négative signifie que les entreprises sont plus susceptibles de réduire rapidement leur effectif que de l’augmenter rapidement, tandis qu’une asymétrie positive indique un plus grand potentiel à la hausse. Si le côté gauche est plus éloigné de l’axe horizontal que le côté droit, la distribution présente une asymétrie négative. Par contre, si le côté droit est plus éloigné que le côté gauche, l’asymétrie de la distribution est positive.

En ce qui concerne la taille de l’entreprise, quatre résultats se distinguent des autres. Premièrement, les taux de croissance médians ( $θ$ =0,5, marqué par un losange dans les graphiques) ont tendance à être plus faibles pour les petites entreprises que pour celles du groupe de référence (graphique 6), et plus élevés pour les grandes entreprises que pour celles du groupe de référence (graphique 7). Les taux de croissance médians diffèrent statistiquement l’un de l’autre pour les classes d’entreprises de petite taille, mais non pour les classes d’entreprises de grande taille. Autrement dit, lorsqu’on tient compte des effets de l’âge, de l’industrie et de la période, une relation positive se dégage entre la taille et la croissance médiane pour les entreprises dont la taille est inférieure à un seuil de taille moyenne, mais non pour les entreprises dont la taille est supérieure au seuil. Ces résultats pour les médianes conditionnelles confirment les constatations de Dixon et Rollin (2012) et de Haltiwanger et coll. (2010) concernant la relation entre la croissance moyenne et la taille.

La deuxième observation est que, si la relation entre la croissance médiane et la taille est statistiquement significative pour les classes d’entreprises de petite taille, l’écart quantitatif entre les taux de croissance médian est faible dans l’ensemble des classes de taille. Les entreprises comptant de 5 à moins de 10 UMM ne grandissent que fractionnellement plus lentement que celles du groupe de référence comptant de 20 à moins de 50 UMM, et même les entreprises comptant 1 000 UMM et plus croissent à peine plus rapidement que le groupe de référence (écart entre les taux de croissance inférieur à 0,01).

La troisième constatation est que la principale différence entre les entreprises appartenant à différentes classes de taille ne concerne pas les entreprises médianes, mais celles dont la croissance ou la réduction de l’effectif est rapide. Les graphiques 6 et 7 montrent que les petites entreprises ont une croissance plus instable que les grandes. Les 10 % d’entreprises comptant moins de 5 UMM, dont la réduction de l’effectif est la plus rapide, rapetissent de 22 % plus rapidement que leurs homologues appartenant au groupe de référence, et les 10 % ayant la plus forte croissance (quantile 0,90) croissent de 6 % plus rapidement. Le graphique 7 montre que la plupart des grandes entreprises qui réduisent rapidement leurs effectifs affichent des taux de croissance qui sont moins négatifs que les entreprises correspondantes du groupe de référence, tandis que celles dont la croissance est la plus forte affichent des taux de croissance qui ont tendance à être moins positifs.

Graphique 6

Description pour graphique 6

Graphique 7

Description pour graphique 7

Enfin, l’effet de la taille sur la croissance des entreprises situées dans les queues présente une asymétrie négative, ce qui signifie que la taille a des conséquences plus importantes pour les entreprises qui réduisent rapidement leurs effectifs que pour celles dont la croissance est forte. La distance par rapport à l’axe horizontal est plus grande pour les quantiles les plus bas que pour les quantiles les plus élevés. Toutes les estimations pour le 25e centile diffèrent statistiquement de zéro, mais ce n’est pas le cas pour les estimations au 75e centile. Il existe une relation entre la taille de l’entreprise et le seuil de taux de croissance dans la queue gauche de 25 % (le taux de croissance au 25e centile est d’autant plus négatif que l’entreprise est petite), mais aucune relation de ce genre n’est observée dans la partie à forte croissance de la distribution. Les petites entreprises sont plus susceptibles de rapetisser rapidement, comme l’illustre la grande distance par rapport à l’axe horizontal pour les quantiles inférieurs. À mesure que la taille augmente, les taux de croissance dans les quantiles inférieurs deviennent moins négatifs.

En résumé, il existe une légère relation positive entre la taille de l’entreprise et la croissance type que connaissent les petites entreprises. Cependant, la différence principale entre les entreprises de diverses tailles est que les petites entreprises sont plus instables. En outre, cette instabilité découle moins d’une plus grande probabilité d’être une entreprise à forte croissance et davantage du plus grand risque de résultats négatifs que courent les petites entreprises. Une explication possible est que les petites entreprises sont moins capables que les grandes de se protéger contre les chocs négatifs. Ou bien, si les chocs négatifs sont corrélés, les entreprises qui réduisent leur effectif sont plus susceptibles d’être petites.

Les profils en fonction de l’âge sont l’opposé des profils en fonction de la taille. Comme l’âge de l’entreprise est une variable de comptage, les coefficients $δ_{1}^{θ}$ et $δ_{2}^{θ}$ peuvent être utilisés pour estimer l’effet pour une entreprise d’un rajeunissement ou d’un vieillissement d’un an. Le graphique 8 représente, pour certains âges, l’effet marginal de divers quantiles, calculés d’après les coefficients estimés :

$E M A_{â g e}^{θ} = - (δ_{1}^{θ} + 2 * δ_{2}^{θ} * â g e)$

$E M A_{â g e}^{θ}$ peut être interprété comme la différence de croissance au quantile $θ$ résultant de la survie une année supplémentaire par rapport à un âge donné.

Le graphique 8 montre que survivre une année supplémentaire réduit l’instabilité des taux de croissance à tous les âges. L’effet de l’âge est étalé vers la droite — surtout pour les très jeunes entreprises, une année d’âge supplémentaire réduit davantage les taux de croissance des entreprises ayant la croissance la plus forte qu’elle ne ralentit le déclin des entreprises réduisant le plus rapidement leur effectif. Le vieillissement de l’entreprise n’a pas d’effet important sur les taux de croissance médians, c’est-à-dire dans la partie de la distribution où se situent la plupart des entreprises.

L’effet du vieillissement de l’entreprise s’aplatit et devient plus symétrique à mesure que l’âge des entreprises augmente. Vieillir d’un an fait varier les taux de croissance de moins de 1 % dans un sens ou dans l’autre pour les entreprises de 15 ans ou plus.

Graphique 8

Description pour graphique 8

Sur le graphique 8, il est difficile de voir l’effet cumulé de nombreuses années d’âge supplémentaire. Le tableau 1 donne les taux de croissance prédits par le modèle de régression pour certaines catégories de taille et d’âge. Il révèle des écarts prononcés entre les entreprises âgées de 2 ans et de 15 ans situées dans les queues de la distribution. Pour les quantiles présentés ( $θ$ = 0,05; 0,10; 0,25; 0,50; 0,75; 0,90 et 0,95), l’écart absolu dans toutes les classes de taille entre ces deux groupes d’âge est de 0,23; 0,14; 0,02; 0,04; 0,14; 0,25 et 0,33, respectivement. Par exemple, pour la taille de référence allant de 20 à moins de 50 UMM, le taux de croissance prédit médian est de 0,03 pour les entreprises âgées de 2 ans comparativement à -0,01 pour celles âgées de 15 ans. Les chiffres correspondants pour le 10e centile sont -0,45 et -0,31, et pour le 90e centile, de 0,50 et 0,25. L’écart est plus important dans la queue droite que dans la queue gauche, et négligeable au centre de la distribution.

Ensemble, les régressions quantiles suggèrent que la taille et l’âge ne donnent lieu qu’à des différences minimales de croissance organique de l’emploi d’une année à l’autre pour la plupart des entreprises, c’est-à-dire celles situées au centre de la distribution. Par contre, ces caractéristiques importent pour les ERR et les EFC¹⁹. Les entreprises deviennent plus stables à mesure qu’elles vieillissent et augmentent de taille. Les différences les plus importantes sont qu’à n’importe quel âge, les petites entreprises sont plus susceptibles de réduire rapidement leur effectif que les grandes, tandis que les jeunes entreprises sont plus susceptibles que les entreprises plus âgées d’avoir une forte croissance.

Tableau 1 Taux de croissance prédits à différents quantiles, selon certaines catégories de taille et d'âge de l'entreprise, Canada, 2000 à 2009

8 Conclusion

La présente étude a pour objectif d’examiner la distribution des taux de croissance des entreprises au Canada de 2000 à 2009. Elle permet de constater que les distributions des taux de croissance de l’emploi au Canada ne sont pas normales ou gaussiennes. Comme il a été constaté pour d’autres pays, leur densité au centre et dans les queues est plus forte que celle de la distribution normale. Les distributions observées donnent à penser que, d’une année à l’autre, la taille de la plupart des entreprises varie très peu, mais que dans une minorité de cas, elle augmente ou diminue rapidement.

La deuxième observation est que les entreprises situées dans les queues représentent une caractéristique importante de la dynamique de l’emploi au Canada, étant à l’origine d’une part importante des emplois créés et détruits au cours de la dernière décennie.

La troisième contribution de la présente étude est l’examen, par des méthodes de régression quantile, du rôle joué par la taille et l’âge dans le rendement des entreprises situées dans les queues de la distribution. Haltiwanger et coll. (2010) et Dixon et Rollin (2012) montrent que la relation en apparence négative entre la taille et la croissance moyenne de l’emploi disparaît lorsque l’âge est ajouté comme variable explicative dans les régressions par les moindres carrés ordinaires (MCO).

Cependant, les résultats présentés ici donnent à penser que ni l’une ni l’autre de ces caractéristiques n’est particulièrement utile pour faire la distinction entre les entreprises situées au milieu de la distribution — les relations entre la croissance de l’emploi et l’âge ainsi que la taille étant plus prononcées dans les queues. Mais leur effet est asymétrique : la petite taille est plus importante que l’âge pour les ERR, tandis que l’âge, ou plus précisément le fait d’être une jeune entreprise, est un meilleur prédicteur de l’appartenance à la catégorie des EFC.

Les résultats ont certaines implications en ce qui concerne les données publiées. Premièrement, l’absence d’une forte relation entre la taille et la croissance de l’entreprise type au Canada entre 2000 et 2009 porte à croire que les résultats moyens sont influencés par des entreprises atypiques. Elle évoque la possibilité que les résultats ambigus concernant la taille et la croissance moyenne publiés pour d’autres pays, industries et périodes puissent refléter les caractéristiques particulières des EFC et à des ERR dans les échantillons employés.

Deuxièmement, une relation négative entre la taille de l’entreprise et la variance de la croissance est décrite dans la documentation existante. Les résultats obtenus dans la présente étude confirment l’existence d’une telle relation pour les entreprises canadiennes. Toutefois, la forte variance observée pour les petites entreprises provient principalement des risques négatifs, tandis que le risque positif est une fonction inverse de l’âge.

L’étude laisse entendre que pour mieux comprendre la dynamique des entreprises, il ne faut pas se limiter à l’examen des premier et deuxième moments de la distribution. Les travaux de recherche à venir se concentreront sur la variation des moments d’ordre plus élevé de la distribution des taux de croissance des entreprises selon l’industrie et au cours du cycle économique.

9 Annexe

Graphique 9

Description pour graphique 9

Graphique 10

Description pour graphique 10

Notes

Les chiffres concernant Google sont tirés de http://www.google.com/about/company/history et des rapports annuels de Google pour 2004, 2010 et 2011, qui peuvent être consultés aux adresses http://investor.google.com\pdf\2004_google_annual_report.pdf; http://investor.google.com\pdf\2010_google_annual_report.pdf; et http://investor.google.com\pdf\2011_google_annual_report.pdf.
Les chiffres pour Research In Motion sont tirés des rapports annuels de 1998 et 2011, qui peuvent être consultés aux adresses http://www.rim.com/investors/documents/pdf/annual/1998rim_ar.pdf et http://www.rim.com/investors/documents/pdf/annual/2011rim_ar.pdf.
Les chiffres pour Nortel proviennent des états financiers annuels de 2008 (http://www.nortel-canada.com/wp-content/uploads/2011/11/2008_nnc_annual_financial_statements.pdf) et du rapport annuel de 2005 (http://www.sec.gov/Archives/edgar/data/72911/999999999706021043/9999999997-06-021043-index.htm).
Stanley et coll. (1996) suggère que la relation entre la variance et la taille pourrait, en fait, être régie par une loi de puissance avec une pente comprise entre -0,17 et -0,21 pour les grandes entreprises américaines. Bottazzi et coll. (2011) constatent une relation similaire pour les entreprises manufacturières françaises, mais Bottazzi et coll. (2007) n’observent aucune relation entre la taille et la variance pour les entreprises manufacturières italiennes. Par contre, Perline et coll. (2006) observent une relation légèrement positive entre la taille et la variance pour un échantillon de petites entreprises américaines.
Pour la théorie des entreprises en tant qu’ensembles de ressources, voir Penrose (1959).
Ces auteurs définissent les entreprises à forte incidence comme étant des entreprises qui ont au moins doublé leurs ventes sur une période de quatre ans, et dont la croissance tant absolue que relative de l’effectif a été importante.
Les estimations portant sur plusieurs années de croissance sont souvent utilisées pour traiter la question de la régression vers la moyenne, qui est fréquente dans les ensembles de données au niveau de l’entreprise.
Voir Baldwin et coll. (1992) pour une description de la construction de la base de données.
Les données administratives du PALE sont structurées au niveau de l’« entreprise statistique », pour laquelle il existe un ensemble complet d’états financiers. Pour simplifier, cette unité statistique est appelée « entreprise » dans la présente étude.
Au Canada, les secteurs de l’enseignement et de la santé sont financés en grande partie par le secteur public. Les entreprises appartenant aux secteurs exclus ont d’autres motivations que celles du secteur des entreprises — elles ne maximisent pas nécessairement les profits.
Aucune mesure directe de l’effectif n’est disponible dans le PALE — l’effectif de l’entreprise est imputé en utilisant l’information annuelle sur la masse salariale.
Si une entreprise est présente dans plusieurs provinces, son nombre national d’UMM correspond à la somme de ses nombres provinciaux d’UMM. En outre, la même catégorie de taille est utilisée dans toutes les provinces, parce que la taille de l’entreprise est considérée comme une caractéristique nationale. Toutefois, l’industrie dominante pour une entreprise donnée peut varier d’une province à l’autre.
L’exclusion des entreprises qui disparaissent un an avant leur disparition nécessiterait l’utilisation de données pour trois années consécutives.
Selon le théorème central limite (TCL), un grand nombre de chocs dont les distributions sont indépendantes devraient résulter en une distribution normale, ou gaussienne, quelles que soient les distributions exactes qui les produisent, à condition qu’aucun des chocs ne soit dominant et que tous aient une variance finie.
Pour des renseignements détaillés sur les distributions de Laplace et les processus stochastiques qui leur donnent naissance, voir Reed (2007).
Les graphiques 4 et 5 ont également été produits en utilisant des classes de taille et d’âge plus étroites. La même tendance a été observée – les queues sont plus lourdes pour les groupes d’entreprises plus petites et plus jeunes.
L’âge maximal qui peut être systématiquement déterminé pour toutes les années étudiées est 16 ans.
Des résultats similaires à ceux exposés dans le présent document ont été obtenus en utilisant un modèle de régression contenant des variables indicatrices utilisant des tranches d’âge plutôt qu’une variable de comptage.
Des régressions quantiles ont été effectuées pour les industries des biens et services séparément, en se servant du même modèle que dans cette étude. Une comparaison des résultats n’a démontré aucune différence entre les profils des deux secteurs.

Date de modification :: 2015-11-27

Sélection de la langue

Recherche et menus

Recherche