Direction des études analytiques : documents de recherche
Réseaux d’entreprises, frontières et intégration économique régionale
 Consulter la version la plus récente.
Consulter la version la plus récente.
Information archivée dans le Web
L’information dont il est indiqué qu’elle est archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Elle n’est pas assujettie aux normes Web du gouvernement du Canada et elle n’a pas été modifiée ou mise à jour depuis son archivage. Pour obtenir cette information dans un autre format, veuillez communiquer avec nous.
Remerciements
Les auteurs remercient Robby Bemrose pour son aide à la création de la base de données sur les réseaux d’entreprises et Steven Brakman pour ses commentaires sur une version antérieure du présent document. Les auteurs reconnaissent également le soutien financier d’Innovation, Sciences et Développement économique Canada, qui a soutenu la production des estimations du commerce interrégional et l’estimation des effets des réseaux d’entreprises sur le commerce.
Résumé
Bien que la présence d’effets de frontières provinciales, à savoir la relative faiblesse du commerce interprovincial comparativement au commerce intraprovincial, soit bien établie, leur cause demeure obscure. Analyser les sources de l’effet des frontières est important, car une telle analyse fournit aux décideurs politiques beaucoup plus de renseignements pour leur permettre d’orienter leurs efforts. Dans ce document, les auteurs font un pas dans cette direction en tâchant de déterminer si une partie de l’effet des frontières peut être attribuée à la manière dont les entreprises à unités multiples organisent leur production à l’intérieur et à l’extérieur des frontières provinciales. Des réseaux d’unités d’exploitation contrôlés par la même entreprise abaissent le coût du commerce en expédiant des biens entre les unités, alors que de la valeur est ajoutée par l’intermédiaire de la chaîne de production ou par l’utilisation de chaînes d’approvisionnement communes en amont et en aval. Les coûts d’exploitation plus élevés de ces réseaux dans de multiples provinces peuvent constituer un obstacle pour les réseaux d’entreprises. En combinant des mesures du commerce régional et des réseaux d’entreprises sur une période de neuf ans (2004 à 2012), l’étude a testé ces propositions. Selon l’étude, alors que de nombreuses entreprises gèrent des réseaux dans de multiples provinces, les réseaux d’entreprises se dissipent aux frontières provinciales et cela a d’importantes répercussions sur le commerce. En outre, si on utilise un modèle gravitationnel, les effets des frontières provinciales chutent de moitié après avoir tenu compte des réseaux d’entreprises. Cela découle à la fois des frontières provinciales constituant un obstacle pour les réseaux d’entreprises et des réseaux qui traversent les frontières provinciales qui agissent moins comme un complément au commerce qu’un substitut pour ce même commerce.
Sommaire
Bien que la présence d’effets de frontières provinciales, à savoir la relative faiblesse du commerce interprovincial comparativement au commerce intraprovincial, soit bien établie, leur cause demeure obscure. Analyser les sources de l’effet des frontières est important, car une telle analyse fournit aux décideurs politiques beaucoup plus de renseignements pour leur permettre d’orienter leurs efforts. Dans ce document, les auteurs font un pas dans cette direction en tâchant de déterminer si une partie de l’effet des frontières peut être attribuée à la manière dont les entreprises à unités multiples organisent leur production à l’intérieur et à l’extérieur des frontières provinciales. Des réseaux d’unités d’exploitation contrôlés par la même entreprise abaissent le coût du commerce en expédiant des biens entre les unités, alors que de la valeur est ajoutée par l’intermédiaire de la chaîne de production ou par l’utilisation de chaînes d’approvisionnement communes en amont et en aval. Les coûts plus élevés d’exploitation de ces réseaux dans de multiples provinces peuvent constituer un obstacle pour les réseaux d’entreprises qui facilitent le commerce. Cet élément peut transformer l’effet complémentaire des réseaux d’entreprises sur le commerce en un effet de substitution pour le commerce. Combinés, une plus faible présence au-delà des frontières provinciales et des effets de substitution de commerce provoqués par des coûts aux frontières peuvent aider à expliquer l’importance de l’effet des frontières provinciales.
Dans le présent document, l’effet des réseaux d’entreprises sur les effets des frontières est examiné en combinant des mesures du commerce régional et des réseaux d’entreprises sur une période de neuf ans (2004 à 2012). Voici, notamment, les questions auxquelles on tente de répondre dans l’étude :
- La distance et les frontières provinciales sont-elles associées à l’élargissement des réseaux d’entreprises des unités d’exploitation dans les régions?
Les liens des réseaux d’entreprises s’affaiblissent avec la distance. Ce point s’applique également aux entreprises qui assument des coûts pour l’organisation de leur production sur de plus grandes distances. Les liens des réseaux d’entreprises faiblissent également quand on passe d’une province à une autre. Après avoir tenu compte de la distance, les liens des réseaux d’entreprises sont environ 19 % plus faibles entre les provinces qu’à l’intérieur de celles-ci, selon l’étude. - Les réseaux d’entreprises agissent-ils comme un complément ou un substitut pour le commerce entre les régions?
Étant donné la distance croissante et la présence de frontières provinciales, l’effet de complémentarité des réseaux d’entreprises sur le commerce diminue. De même, à des distances suffisamment longues et quand le commerce se fait entre les provinces, les réseaux passent d’un état de complément à un de substitut pour le commerce. Autrement dit, quand un échange commercial se produit à plus de 1 200 km et traverse une frontière provinciale, l’effet des réseaux d’entreprises sur le commerce passe de celui de complément à celui de substitut. Pour de nombreuses relations commerciales provinciales importantes (p. ex. les relations Alberta-Ontario), l’effet du réseau d’entreprises sur le commerce est négatif. - Dans quelle mesure les réseaux d’entreprises tiennent-ils compte de l’effet des frontières provinciales?
Toutes choses étant égales par ailleurs, le commerce entre les frontières provinciales représente environ 60 % du commerce intraprovincial. Toutefois, lorsque la force des liens des réseaux d’entreprises est prise en considération, cette proportion augmente pour se situer à 80 %.
1 Introduction
Les coûts du commerce se sont révélés avoir un effet important sur le degré d’intégration économique entre les régions et les pays (Anderson et van Wincoop, 2004; Chaney, 2008; Behrens et Brown, 2018). Bien que l’ampleur de ces coûts puisse être estimée assez facilement, leurs sources sont beaucoup plus difficiles à discerner. En outre, bien que les coûts de transport au Canada représentent une contribution importante aux coûts du commerce totaux (Behrens et Brown, 2018)Note 1, la forte présence d’effets des frontières provinciales donne à penser qu’il faut quand même tenir compte d’autres facteurs (Bemrose, Brown et Tweedle, 2017). Contrairement aux États-Unis, où des données et des méthodes raffinées ont réduit à zéro les estimations des effets des frontières à l’échelle des États (Hillberry et Hummels, 2008), au Canada, on retrouve encore des indications que les frontières provinciales ont de l’importance (Agnosteva, Anderson et Yotov, 2014; Albrecht et Tombe, 2016), les effets mesurant environ 6,9 % en termes d’équivalents tarifaires (Bemrose, Brown et Tweedle, 2017). La question suivante est évidente : « Quels sont les coûts du commerce qui sous-tendent ces effets de frontière? » ou, peut-être plus précisément dans ce cas, « Est-ce que les frontières et les coûts qu’elles entraînent pour les entreprises interviennent pour réduire la capacité des entreprises à atténuer les coûts du commerce? »
Parmi les coûts du commerce les plus importants, on retrouve ceux que les entreprises assument quand elles se livrent à des transactions commerciales (Williamson, 1979) qui, à leur tour, influencent les structures des échanges (Rauch, 1999). Pour minimiser ces coûts, il se révèle parfois avantageux pour l’entreprise d’étendre ses activités au-delà des frontières. Comme les entreprises prennent de l’expansion dans de nouvelles régions, le commerce peut être induit au moment où elles s’engagent dans des échanges intra-entreprises à faible coût ou qu’elles élargissent leurs chaînes d’approvisionnement existantes. Dans le premier cas, il convient de mentionner qu’environ un tiers du commerce international se produit à l’intérieur des entreprises (Antràs, 2003; Antràs et Helpman, 2004). Dans le second cas, il est démontré que les entreprises qui sont reprises adaptent par la suite leurs technologies de production, y compris les destinations d’expédition en aval et probablement leurs chaînes d’approvisionnement en amont, pour correspondre plus étroitement à celles de l’entreprise qui les acquièrent (Atalay, Hortaçsu et Syverson, 2014).
Bien que le rôle du commerce intra-entreprise sur la scène internationale soit bien connu, on en connaît relativement peu sur le rôle du commerce intra-entreprise au niveau infranational (Anderson, 2011; Atalay, Hortaçsu et Syverson, 2014), ou, de façon plus générale, sur l’effet des réseaux d’entreprises sur le commerce. En particulier, un facteur qui sous-tend l’intégration des économies provinciales par le commerce de biens peut être important : les liens intra-entreprises qui s’étendent au-delà des frontières provinciales ou l’absence de tels liens (Helliwell,1998). En conséquence, le présent document vise à examiner la nature des réseaux d’entreprises au Canada, leur relation avec le commerce régional de biens et dans quelle mesure ces réseaux tiennent compte de l’effet des frontières régionales sur les flux des échanges. En particulier, l’analyse aborde les questions suivantes :
- Dans quelle mesure la cohésion d’une économie provinciale est-elle assurée par des entreprises à emplacements multiples (réseaux d’entreprises)?
- Avec quelle facilité ces réseaux d’entreprises dépassent-ils les frontières provinciales? Autrement dit, comme pour le commerce, les réseaux d’entreprises (c.-à-d. les emplacements d’exploitation contrôlés par la même entreprise) peuvent être plus courants à l’intérieur des frontières provinciales, car les entreprises peuvent engager des frais supplémentaires lorsqu’elles se lancent sur de nouveaux marchés provinciaux (p. ex. l’adaptation à un nouvel ensemble de règlements). Par ailleurs, ils peuvent être plus courants quand l’accès aux marchés (p. ex. l’admissibilité à soumissionner pour des contrats gouvernementaux) passe par la démonstration d’une présence physique dans la province (Chaundy, 2016).
- Dans quelle mesure ces réseaux d’entreprises influencent-ils l’intégration provinciale par le commerce de biens? Plus particulièrement, dans quelle mesure les réseaux d’entreprises tiennent-ils compte des effets des frontières provinciales? Les réseaux d’entreprises améliorent-ils le commerce en réduisant les coûts de transaction ou réduisent-ils les échanges en permettant aux entreprises d’économiser sur les coûts du commerce en produisant des biens dans les marchés locaux?
Pour aborder ces questions, des renseignements sur le commerce de biens et les réseaux d’entreprises dans les régions sont examinés. Le commerce est mesuré en utilisant le Fichier des transports terrestres (FTT) nouvellement créé par Statistique Canada, lequel se construit depuis un ensemble de dossiers de transactions codées géographiquement pour former un ensemble cohérent d’évaluations de la valeur du commerce dans les régions. Les réseaux d’entreprises sont mesurés en utilisant le Registre des entreprises (RE), lequel contient des renseignements sur la structure des entreprises (c.-à-d. les entreprises et les unités d’exploitation qu’elles contrôlent [c.-à-d. les usines de production]) et l’emplacement des unités d’exploitation. En utilisant une géographie commune, ces deux ensembles de données peuvent être combinés pour fournir une mesure des liens commerciaux entre les régions et les liens d’entreprises. En outre, les deux fichiers couvrent une période de neuf ans (2004 à 2012), procurant des mesures sur les réseaux d’entreprises et le commerce en fonction du temps au moyen d’un panel géographiquement uniforme de régions. Bien que la période de l’étude se termine en 2012, la valeur de l’analyse repose sur la révélation de la relation sous-jacente entre les réseaux d’entreprises, le commerce et les effets des frontières provinciales qui ne varieront probablement pas au fil du temps.
Ces travaux contribuent à deux grands domaines de recherche : les frontières et les obstacles au commerce ainsi que les réseaux d’entreprises.
1.1 Frontières et obstacles au commerce
Tenir compte des réseaux d’entreprises peut aider à analyser l’effet des frontières provinciales. Les obstacles génériques au commerce ont été examinés dans plusieurs études et peuvent être importants (pour en avoir un aperçu, veuillez consulter Anderson et van Wincoop, 2004). Tout naturellement, les entreprises cherchent à minimiser ces coûts. Les multinationales, par exemple, peuvent utiliser des filiales pour réduire les coûts du commerce associés à des problèmes d’exécution de contrats (Yeaple, 2013). À cet égard, les entreprises comptant des chaînes d’approvisionnement intégrées s’élargissent et s’engagent dans le commerce intra-entreprise pour minimiser de tels coûts; cette approche mène à la complémentarité de l’investissement et du commerce. Toutefois, une recherche récente a montré que ce commerce intra-entreprise ne fait pas toujours partie de la chaîne d’approvisionnement, même quand la filiale est une industrie en amont de l’entreprise canadienne (Ramondo, Rappoport et Ruhl, 2016), un résultat qui semble s’appliquer également aux entreprises canadiennes intégrées verticalement (Atalay, Hortaçsu et Syverson, 2014). La signification de cette documentation est que l’incidence des réseaux d’entreprises sur le commerce pourrait se révéler moindre que ce que nous avions pensé au départ.
Tout de même, la relation entre les réseaux d’entreprises et le commerce pourrait aller au-delà de cette vision plus limitée. L’asymétrie de l’information qui, par exemple, prend la forme de relations qu’ont les entreprises dans différentes destinations de commerce, a été utilisée pour expliquer la structure du commerce international (Chaney, 2014). La propriété des entreprises permet à une entreprise d’accroître la connaissance locale des destinations, en réduisant cette asymétrie informationnelle, ce qui incite au commerce entre les régions. En outre, si les entreprises maintiennent leur réseau de fournisseurs en amont, c’est-à-dire leur chaîne d’approvisionnement, alors qu’elles élargissent leur réseau d’emplacements d’exploitation vers l’extérieur, le commerce peut être induit. Ainsi, que ce soit par atténuation des coûts des transactions intra-entreprises, par réduction de l’asymétrie informationnelle ou par élargissement des chaînes d’approvisionnement, l’expansion des réseaux d’entreprises peut être complémentaire au commerce.
Par ailleurs, les entreprises peuvent également utiliser leurs filiales locales pour neutraliser les obstacles commerciaux. Elles peuvent le faire pour surmonter les coûts de transport, pour adapter leurs produits et services aux besoins locaux (p. ex. pour tenir compte des différences dans la réglementation), ou pour satisfaire aux exigences en matière de contenu local pour certains contrats gouvernementaux (Chaundy, 2016). De ce point de vue, le commerce et l’investissement peuvent constituer des substituts. Si l’influence principale des réseaux d’entreprises sur le commerce est complémentaire, ces réseaux peuvent aider à tenir compte des effets des frontières provinciales dans les cas où il est moins probable que ces entreprises étendent leurs activités à d’autres provinces. Bien sûr, l’inverse est vrai s’il existe des substituts.
Le présent document contribue à l’étude des obstacles commerciaux, car on y examine l’association des réseaux d’entreprises avec des obstacles au commerce provincial au Canada. Il s’apparente étroitement à la littérature qui établit un lien entre les réseaux d’affaires et les réseaux sociaux d’immigrants et le commerce agrégé, à commencer par Rauch (1999, 2001). L’idée est que les immigrants établissent des liens entre leurs contacts dans leur pays d’origine et leur nouveau pays et que les pays fassent plus de commerce qu’ils n’en auraient fait autrement sans ces liens. Toutefois, cette étude est axée sur un canal particulier d’une entreprise propriétaire d’emplacements d’exploitation dans différentes régions et sur l’effet cumulatif de ces liens sur le commerce régional. À cet égard, ce travail a beaucoup en commun avec Combes, Lafourcade et Mayer (2005), qui ont constaté que les réseaux d’entreprises et la migration réduisaient les obstacles intranationaux mesurés, et Germendia et coll. (2012), qui ont examiné l’effet des réseaux et de la migration et découvert que ceux-ci réduisaient les effets des frontières provinciales espagnoles, les réseaux d’entreprises étant plus importants. Toutefois, le présent document va au-delà du travail de Combes, Lafourcade et Mayer (2005) et Garmendia et coll. (2012) en utilisant des méthodes par panel pour réguler l’endogénéité et aborder des questions relatives à la complémentarité et à la substituabilité entre l’investissement et le commerce régional de biens.
1.2 Réseaux d’entreprises
De nombreuses études ont porté sur les réseaux d’entreprises, leurs caractéristiques et leurs répercussions sur la productivité et le commerce. Dans ce cas, les caractéristiques spatiales suscitent un intérêt, mais les travaux actuels sont également liés aux champs de recherche plus vastes abordés dans ces études.
En termes descriptifs, Atalay et coll. (2011) ont démontré la prévalence des réseaux d’entreprises et leurs relations à la taille des entreprises (sur le plan des relations avec les clients et les fournisseurs), et Lim (2017) a démontré les répercussions des coûts fixes sur l’établissement des relations entre entreprises. Un résultat important de l’étude est qu’il a été démontré que la réduction des coûts du commerce dans la chaîne d’approvisionnement augmente la productivité des entreprises dans les réseaux d’entreprises japonais (Bernard, Moxnes et Saito, 2015), ce qui complète le travail antérieur sur les keiretsu japonais (Belderbos et Sleuwaegen, 1996, 1998; Head, Ries et Spencer, 2004). Ces résultats portent à croire que des obstacles provinciaux entravent l’établissement de réseaux d’entreprises et, en fin de compte, que les économies en ce qui concerne les coûts du commerce peuvent avoir des répercussions sur la productivité.
S’appuyant sur ces résultats, les auteurs de l’étude ont pris du recul pour examiner les réseaux eux-mêmes, plus particulièrement l’importance de la distance et des frontières. Cela est crucial car, pour que les réseaux d’entreprises comptent pour le commerce transfrontalier, ils doivent également être moins courants au-delà des frontières. La documentation existante n’aborde pas cet aspect et c’est sur ce point que repose une contribution supplémentaire. Cela a trait aux travaux portant sur le choix d’une entreprise multinationale d’ouvrir une nouvelle filiale étrangère (investissement en installations nouvelles) ou de prendre le contrôle d’un emplacement existant (c.-à-d. par des fusions et des acquisitions). Le fait que les fusions et les acquisitions représentent une forme dominante d’investissement direct étranger donne à penser qu’une entreprise multinationale a recours à une acquisition pour partiellement surmonter les obstacles réglementaires et informationnels que la frontière représente (Nocke et Yeaple, 2007), car il doit être plus facile de respecter la réglementation locale en acquérant quelque chose qui existe déjà et qui respecte déjà cette réglementation.
Le reste du présent document est structuré de la façon suivante. La section 2 s’inspire de la documentation théorique et empirique sur les multinationales pour échafauder un ensemble d’hypothèses sur l’élargissement de réseaux d’entreprises au-delà de l’espace et des frontières et la relation entre les réseaux d’entreprises et le commerce. La section 3 porte sur les sources de données et les méthodes utilisées pour mesurer les réseaux d’entreprises. La section 4 fournit une description des réseaux d’entreprises provinciaux et une analyse économétrique des facteurs qui influencent les réseaux d’entreprises à l’échelle provinciale et dans des régions plus définies. La section 5 présente les répercussions des réseaux d’entreprises sur le commerce. Elle est suivie des conclusions (section 6) et de l’annexe.
2 Entreprises à unités multiples et commerce
Pour mettre le présent document en contexte, il est nécessaire de retourner aux raisons fondamentales pour lesquelles les entreprises choisissent d’exploiter des unités multiples et les raisons pour lesquelles, parfois, il est avantageux de localiser des unités à l’extérieur des frontières, que ce soit à l’échelle nationale ou infranationale et d’examiner ce que cette approche sous-entend au sujet du commerce interrégional. Il est utile d’aborder ces questions et leurs hypothèses tacites de manière séquentielle, plutôt que de les traiter toutes en même temps.
2.1 Pourquoi les entreprises ont-elles recours à des unités multiples?
On trouve trois types d’entreprises à unités multiplesNote 2 (Caves, 1996) : 1) horizontales (unités qui produisent les mêmes biens ou services), 2) verticales (unités qui sont reliées fonctionnellement par des liens amont-aval) et 3) diversifiées (unités qui ne sont reliées ni horizontalement ni verticalement; les investissements peuvent être perçus comme une stratégie de diversification du portefeuille). Dans le cas présent, l’accent est mis sur les entreprises liées horizontalement et verticalement. Les entreprises se structurent horizontalement pour internaliser le marché pour des actifs propres, alors que celles qui se structurent verticalement internalisent les marchés pour des biens intermédiaires. Toutefois, les entreprises liées verticalement n’ont pas nécessairement besoin de faire du commerce en interne, car
« [...] il peut y avoir des économies de coûts de transactions dans l’approvisionnement des matières premières qui vont au-delà des intrants nécessaires de la simple production d’une usine. Il est possible de réaliser des économies dans le réseau de transport pour des expéditions de biens finis qui vont au-delà de la simple production d’une usine. » (Caves, 1996, p. 6.)
Cela correspond aux données sur la structure des échanges intra-entreprises nationaux (Atalay, Hortaçsu et Syverson, 2014) et internationaux (Ramondo, Rappoport et Ruhl, 2016). En outre, les économies réalisées en élaborant une structure liée horizontalement ou verticalement doivent être comparées aux coûts de gestion de ces activités. Comme ces coûts augmentent, les entreprises ont plus tendance à effectuer davantage de transactions sans lien de dépendance. Une dimension à laquelle on pourrait s’attendre (Duranton et Puga, 2005) et pour laquelle on pourrait découvrir (Behrens et Sharunova, 2015; Baldwin et Brown, 2005) des indications que des coûts de gestion sont effectivement à la hausse est la distance entre les unités. Par exemple, des unités d’exploitation d’une entreprise à unités multiples sont plus compactes géographiquement qu’un ensemble sélectionné aléatoirement d’entreprises à une seule unité dans la même industrie (Behrens et Sharunova, 2015). Bien entendu, on comprend que, comme la distance entre des unités probables augmente, les avantages d’internaliser les marchés pour des actifs propres sont proportionnellement plus susceptibles d’être dépassés par le coût de gestion d’activités éloignées. Cela mène à la première hypothèse de l’étude.
Hypothèse 1 (H1) : Un compromis entre des économies réalisées de l’exploitation d’entreprises à unités multiples et le coût de gestion de ces activités devant être envisagé, la fréquence des liens des réseaux d’entreprises chutera avec la distance entre les régions.
2.2 Quand les entreprises étendent-elles leurs activités au-delà des frontières?
Lorsqu’il traverse les frontières, l’entrepreneur doit assumer des coûts fixes supplémentaires pour apprendre la manière de fonctionner dans un secteur de compétence différent, que ce soit un pays ou une province dans ce cas.
« L’entrepreneur type, originaire d’un quelconque pays particulier, apporte à ses activités commerciales des connaissances générales acquises dans son système juridique et social et sa “façon particulière de faire les choses”. » (Caves, 1996, p. 57 et 58.) L’avantage que comportent les coûts de transaction de l’entreprise à unités multiples est requis pour contrebalancer ces coûts. Les mêmes principes s’appliquent aux marchés nationaux. « En effet, l’expansion initiale des entreprises à un statut de marché national dans l’économie américaine du 19e siècle a été apparemment assez semblable à leur évolution au statut d’entreprise multinationale plus récemment. » (Kindleberger, 1969, p. 33 à 35.) Ce compromis mène à la deuxième hypothèse.
Hypothèse 2 (H2) : Les entreprises sont moins susceptibles d’établir des réseaux d’entreprises au-delà des frontières provinciales, en raison du coût d’exploitation plus élevé dans plusieurs provinces.
La relation opposée pourrait tenir si les règles d’approvisionnement du gouvernement stipulaient que les entreprises doivent avoir une présence physique dans une province pour être admissibles à des contrats (Chaundy, 2016). Il est peu probable que cette forme particulière de règle de passation des marchés détermine la structure globale d’investissement. Par conséquent, l’hypothèse H2 est conservée comme hypothèse principale.
2.3 De quelle manière les réseaux d’entreprises influencent-ils le commerce?
On relève deux perspectives pertinentes. La première est un modèle de base de commerce et d’investissement qui peut s’appliquer pour démontrer que les coûts croissants du commerce (p. ex. les tarifs ou les coûts de transport) se traduiront par une baisse des exportations qui correspond à une hausse de la production locale. Ainsi, des coûts croissants du commerce transforment l’effet des réseaux d’entreprises qui passe de l’état de complément au commerce à un état de substitut pour celui-ci. Cette relation linéaire se maintient lorsqu’on observe une baisse des rendements d’échelle, mais ne se produit pas lorsqu’on observe des rendements croissants, une situation où la production se fait soit sur le plan national soit à l’étranger. Brainard (1997) a montré que les ventes des entreprises affiliées d’entreprises multinationales américaines (comme une proportion de ces ventes plus les exportations américaines) augmentaient avec les coûts de transport. La conclusion plus générale qui en découle est que plus les coûts du commerce sont élevés, plus grande est la proportion des ventes des entreprises multinationales dans le pays hôte dans lequel cette production est comptabilisée comme étant locale. L’hypothèse suivante repose sur cette constatation.
Hypothèse 3 (H3) : Des coûts du commerce plus élevés, associés à la distance ou aux frontières, pour une entreprise donnée, transforment l’effet des réseaux d’entreprises sur le commerce qui passe de positif à négatif (de complément à substitut).
La seconde perspective est plus subtile, mais pourrait être aussi importante ou plus importante. Conformément au cadre de la Transaction Cost Economics (TCE), les entreprises s’organisent pour minimiser « [...] les coûts de production et les activités logistiques associées de l’entreprise » (Caves, 1996, p. 2, caractères gras ajoutés). Un des avoirs particuliers de l’entreprise qui contribuent à l’expansion horizontale ou verticale des activités de l’entreprise est sa capacité logistique telle qu’exprimée par sa chaîne d’approvisionnement. Pour les entreprises de vente au détail et en gros, leur capacité à monter et à gérer des chaînes d’approvisionnement est probablement un de leurs atouts les plus importants. Selon la perspective de la TCE, même quand il n’existe aucun lien de propriété, le besoin d’une certaine forme d’entente contractuelle signifie que le changement de fournisseurs a un coût (Williamson, 2008). En fait, Atalay, Hortaçsu et Syverson (2014) ont constaté que, après l’achat d’une unité, sa technologie de production et ses destinations d’expédition ressemblent de plus en plus à celles de l’entreprise qui l’acquiert. Ainsi, les entreprises, indépendamment de leurs structures horizontales ou verticales, tendent à maintenir leurs chaînes d’approvisionnementNote 3. Comme les entreprises s’étendent à de nouveaux domaines (ou contrats), il en va de même pour leurs chaînes d’approvisionnement. Par conséquent, même en l’absence de relation intrants-extrants entre les unités, le commerce entre les régions peut augmenter simplement parce que les entreprises ont un réseau établi de fournisseurs qui les suit. Toutefois, encore une fois, un coût accompagne le maintien de ces réseaux dans l’espace, et sur des distances plus longues, il est moins probable que ceux-ci seront maintenus, car les coûts supplémentaires de transport dépassent les coûts d’utilisation moindres d’un réseau existant de fournisseurs. Cela nous mène à la quatrième et dernière hypothèse.
Hypothèse 4 (H4) : L’effet des réseaux d’entreprises sur le commerce diminue avec la distance, alors que le coût de maintien des chaînes d’approvisionnement l’emporte sur leurs avantages.
Bien entendu, les hypothèses H3 et H4 sont équivalentes d’après ce que l’on a observé. Ainsi, il ne sera pas possible d’établir une distinction entre les deux processus. Toutefois, il sera possible d’établir si des relations commerciales dans l’espace cadrent avec les deux.
3 Méthodologie
L’analyse est fondée sur la mesure des réseaux d’entreprises et le commerce entre les régions. Le premier nécessite des renseignements détaillés sur la structure des entreprises et leurs emplacements, alors que le second nécessite des renseignements sur le commerce de biens dans une unité géographique similaire. Chacune de ces sources de données est décrite de façon séquentielle ci-dessous, en commençant par les réseaux d’entreprises.
3.1 Définir et mesurer les réseaux d’entreprises
L’étude cherche à mesurer à quel point les régions sont liées par des réseaux d’entreprises et à mesurer l’association entre ces réseaux et le flux des échanges. Par leur nature même, les réseaux d’entreprises sont constitués d’entreprises à unités multiples ou de ce qu’on appellera ici des « entreprises à emplacements multiples » afin de respecter les règles d’affectation des noms du RE. Deux unités géographiques sont liées si des emplacements d’exploitation dans chacune d’elles font partie de la même entreprise (à emplacements multiples). Par exemple, Toronto et Halifax sont liées par un réseau d’entreprises si une chaîne de supermarchés gère des emplacements aux deux endroits. Une manière simple de mesurer des réseaux d’entreprises entre deux régions est de compter le nombre d’emplacements d’exploitation d’une unité géographique qui font partie de la même entreprise à unités multiples exerçant ses activités dans les deux régions.Note 4
La figure 1 illustre ce point sur le plan conceptuel. Une entreprise a un emplacement dans la région et deux emplacements dans la région , alors que l’entreprise a deux emplacements dans la région et la région . Ainsi, du point de vue de la région , le nombre d’emplacements liés à est de trois, alors que le nombre d’emplacements dans la région liés à est de quatre. Il convient de noter que l’entreprise à emplacements multiples a un emplacement à , mais aucun à , et ainsi ses emplacements ne sont pas comptés lorsque nous tenons compte des emplacements dans liés à . En termes officiels, la force des connexions d’un réseau d’entreprises () de la région à la région pour chaque entreprise est calculée de la manière suivante :
(1)
Où est le nombre d’emplacements d’exploitation de l’entreprise dans la région . Comme cela ressort de cette équation et de l’exemple décrit ci-dessus, les liens d’entreprises sont bidirectionnels, mais asymétriques.
L’équation (1) est utilisée pour l’analyse des réseaux d’entreprises entre des unités géographiques pour deux raisons. En premier lieu, elle peut être dérivée d’un modèle de formule réduit, dont les détails sont présentés dans la sous-section 4.1. En second lieu, elle sert de fondement à l’analyse de la relation entre les réseaux d’entreprises et les flux des échanges qui nécessitent que les mesures des réseaux se fassent d’une manière légèrement différente.

Description de la figure 1
Le titre de la figure 1 est « Réseaux d’entreprises conceptuels ».
Le diagramme illustre des emplacements possibles de différentes entreprises dans différentes régions.
On retrouve trois régions, représentées par des hexagones, portant les mentions « Région », « Région » et « Région » . Les hexagones sont contigus (ils sont joints sur deux côtés) et sont représentés par une ligne noire.
Dans la région : l’entreprise a un emplacement , l’entreprise a deux emplacements et l’entreprise a un emplacement .
Dans la région : l’entreprise a deux emplacements , l’entreprise a deux emplacements et l’entreprise n’a aucun emplacement.
Dans la région : l’entreprise a un emplacement (), l’entreprise a deux emplacements (, ) et l’entreprise a un emplacement ().
La source de ce diagramme est « Statistique Canada, composition des auteurs ».
Selon l’équation (1), le commerce serait tributaire de la présence d’un réseau d’entreprises et de la pondération de la taille de l’entreprise telle que mesurée par le nombre de ses emplacements d’exploitation dans . Toutefois, sur la base de paires, l’effet des réseaux sur le commerce dépend des emplacements de l’entreprise dans les deux régions. Une façon simple de saisir les liens d’entreprises bilatéraux des régions et est de tenir compte de l’asymétrie sous-entendue par l’équation (1) pour également saisir les liens de à :
(2)
La mesure additive agrégée représente ainsi la totalité des liens entre et , où est une mnémonique pour « additive ». Cette mesure additive donne probablement une bonne représentation des connaissances accumulées des entreprises sur les marchés dans les deux régions, mais elle ne tient pas entièrement compte du potentiel du commerce intra-entreprise, car on ne prend pas en considération la taille et les industries auxquelles les emplacements appartiennent.
Il est possible d’utiliser d’autres méthodes de mesure des réseaux d’entreprises. L’étude évalue plusieurs spécifications différentes, y compris la restructuration du problème en matière de définition mathématique type d’un réseau (un ensemble de nœuds et d’arêtes), et vérifie les différentes manières de pondérer les liens pour tenir compte du nombre d’emplacements et de la taille des entreprises qui peuvent caractériser le potentiel de commerce. Les résultats de ces spécifications sont similaires; ces formulations et résultats sont présentés dans l’annexe.
3.2 Données
Ces mesures des réseaux d’entreprises nécessitent une méthode d’identification des entreprises à unités multiples dans des régions infranationales. Le Registre des entreprises (RE) de Statistique Canada est un répertoire qui contient toutes les entreprises au Canada, dans lequel les entreprises sont définies comme étant à unités multiples si elles ont plus d’un emplacement d’exploitation. Par exemple, une entreprise manufacturière est considérée comme étant à unités multiples si elle possède plus d’une usine (emplacement d’exploitation). Mesurer les réseaux d’entreprises à partir du RE est possible, car il procure des renseignements sur la structure d’exploitation d’une entreprise, son emplacement géographique et son industrie (niveau à six chiffres du Système de classification des industries de l’Amérique du Nord). En utilisant les renseignements sur la géographie et l’industrie également disponibles, il est alors possible d’évaluer si une telle entreprise exploite des emplacements à l’intérieur d’une ou de plusieurs unités géographiques, par industrie.
Au fil du temps, le RE a subi des modifications qui ont amélioré la couverture statistique des entreprises au Canada. Toutefois, sur le plan analytique, cela représente un défi, car des modifications apportées à la structure des entreprises peuvent compromettre la cohérence longitudinale du RE. Par exemple, l’inclusion de données fiscales détaillées supplémentaires (relevés T4) dans le RE en 2009 a amélioré la couverture des entreprises à provinces multiples. Toutefois, cela donne lieu à de nombreuses créations longitudinalement contradictoires d’emplacements appartenant à des entreprises à unités multiples en 2008 et en 2009. Pour améliorer la cohérence longitudinale du fichier, des indicateurs accessibles dans le RE ont été utilisés pour exclure des entreprises touchées par des modifications dans la structure du RE. La période de 2004 à 2012 est utilisée de sorte qu’elle coïncide avec la période couverte par le FTT, qui est employée pour mesurer le flux des échanges régionaux.
3.2.1 Ventilation sectorielle
L’étude est axée sur le secteur des entreprises et offre une ventilation sectorielle, définie comme suit : une entreprise à unités multiples est dite être dans le secteur des biens si chacun de ses emplacements d’exploitation produit des biens. De même, une entreprise à unités multiples appartient au secteur des services si tous ses emplacements d’exploitation sont dans le secteur des services. Les entreprises à unités multiples qui ont à la fois des emplacements d’exploitation produisant des biens et des services sont dites être dans le secteur des biens hybrides, car elles sont liées à la fois au secteur des biens et au secteur des services. Il convient de noter que le secteur des biens hybrides contient uniquement des emplacements qui appartiennent à des entreprises à unités multiples. En moyenne au cours de la période allant de 2004 à 2012, les entreprises de secteur des services seulement constituaient presque 75 % des emplacements d’exploitation du secteur des entreprises. On compare cela à 23,2 % des emplacements d’exploitation dans le secteur des biens seulement et à 2,2 % des emplacements d’exploitation dans le secteur des biens hybrides (voir le tableau 1).
| Secteur | Part en pourcentage des emplacements d’exploitation |
|---|---|
| pourcentage | |
| Biens seulement | 23,2 |
| Biens hybrides | 2,2 |
| Services seulement | 74,6 |
| Ensemble du secteur des entreprises | 100,0 |
| Source : Statistique Canada, calculs des auteurs. | |
Cette répartition par industrie pourrait avoir un effet important, car on s’attend à ce que les entreprises se comportent différemment dans le secteur des entreprises. Par exemple, les producteurs de biens qui sont incités à garder leurs installations de production à proximité pour minimiser les coûts de gestion de leurs installations (Duranton et Puga, 2005) ou de tirer avantage des économies des divers emplacements (p. ex. liens amont-aval, bassin de main-d’œuvre et retombées de connaissances). En revanche, les fournisseurs de services ne sont pas confrontés aux mêmes coûts de gestion d’unités multiples à diverses distances, car le processus de production est souvent (mais pas toujours) moins compliqué que celui de la production de biens. L’expansion des entreprises de biens et de services dans de nouveaux marchés peut également produire un effet différentiel sur le commerce. Pour de nombreuses entreprises de services, en raison du fait qu’elles nécessitent un contact avec le client (p. ex. les magasins de détail), une expansion entraîne habituellement la recherche de nouveaux marchés géographiques, tout en tentant de ne pas empêcher les clients de se rendre dans des installations existantes (effet de substitution).
Bien entendu, l’expansion des entreprises de services peut également induire le commerce si l’expansion dans de nouvelles régions comporte l’extension de chaînes d’approvisionnement existantes. Les mêmes mesures incitatives peuvent également valoir pour les entreprises produisant des biens, mais une expansion peut également induire plus d’échanges commerciaux par le commerce en amont et en aval au sein de l’entreprise (effet complémentaire). En dernier lieu, par rapport au secteur des biens hybrides, comme les entreprises de ce secteur sont par définition à unités multiples, elles sont probablement de plus grande taille que les entreprises de biens seulement ou de services seulement. Ainsi, bien qu’elles soient également confrontées à des coûts de gestion d’unités multiples, elles ont probablement la capacité d’absorber ces coûts s’ils sont fixes. En conséquence, il est possible que ces entreprises étendent plus facilement leurs activités aux autres provinces. La façon dont l’expansion des entreprises à unités multiples est liée au commerce dépendra de la concentration relative des unités produisant des biens et des services à l’intérieur de l’entreprise même et, par conséquent, il s’agit d’une question empirique.
3.3 Données sur le commerce
Le Fichier des transports terrestres (FTT) de Statistique Canada est utilisé pour mesurer les flux des échanges régionaux (veuillez consulter l’annexe pour obtenir plus de renseignements sur le montage du fichier). Il s’agit d’une base de données sur le commerce régional au Canada de 2004 à 2012, laquelle englobe les biens transportés par camion et par chemin de fer. Les flux des échanges sont calculés en fonction des échanges interprovinciaux et intraprovinciaux totaux par produit de base et par année pour mieux rendre compte du commerce total de biens au Canada. La base de données contient des données sur les expéditions mesurées en fonction du produit de base, du tonnage, de la valeur, de la distance et du coût entre les points d’origine et de destination géocodés. Ces derniers permettent de mesurer le commerce entre un nombre pratiquement illimité de régions. Cela est important à la lumière des problèmes associés à l’agrégation géographique, notamment le problème de l’unité de surface modifiable. De façon générale, la manière de préciser les unités géographiques, qu’elles soient standard ou non, importe et peut avoir des répercussions sur les modèles d’interaction spatiale comme le modèle gravitationnel utilisé dans la présente étude.
Dans cette optique, l’étude fait appel à deux unités géographiques standard, soit les provinces et les grandes régions économiques (GRE), et à une unité géographique non standard, à savoir des grilles hexagonales (voir carte 1), pour mesurer les flux des échangesNote 5. L’étude suit l’approche de Bemrose, Brown et Tweedle (2017) en utilisant des grilles hexagonales de 225 km de côté. À l’aide des codes postaux des emplacements d’exploitation, des GRE et des unités géographiques hexagonales sont créées. Sans l’éliminer complètement, cette stratégie aide à atténuer la sensibilité des résultats à des biais associés à l’agrégation géographique qui altèrent les unités géographiques standard, puisque les hexagones sont identiques et spatialement indépendants (Arbia, 1989). Il convient de noter que les hexagones qui traversent les frontières provinciales sont séparés et traités comme des unités géographiques distinctes.
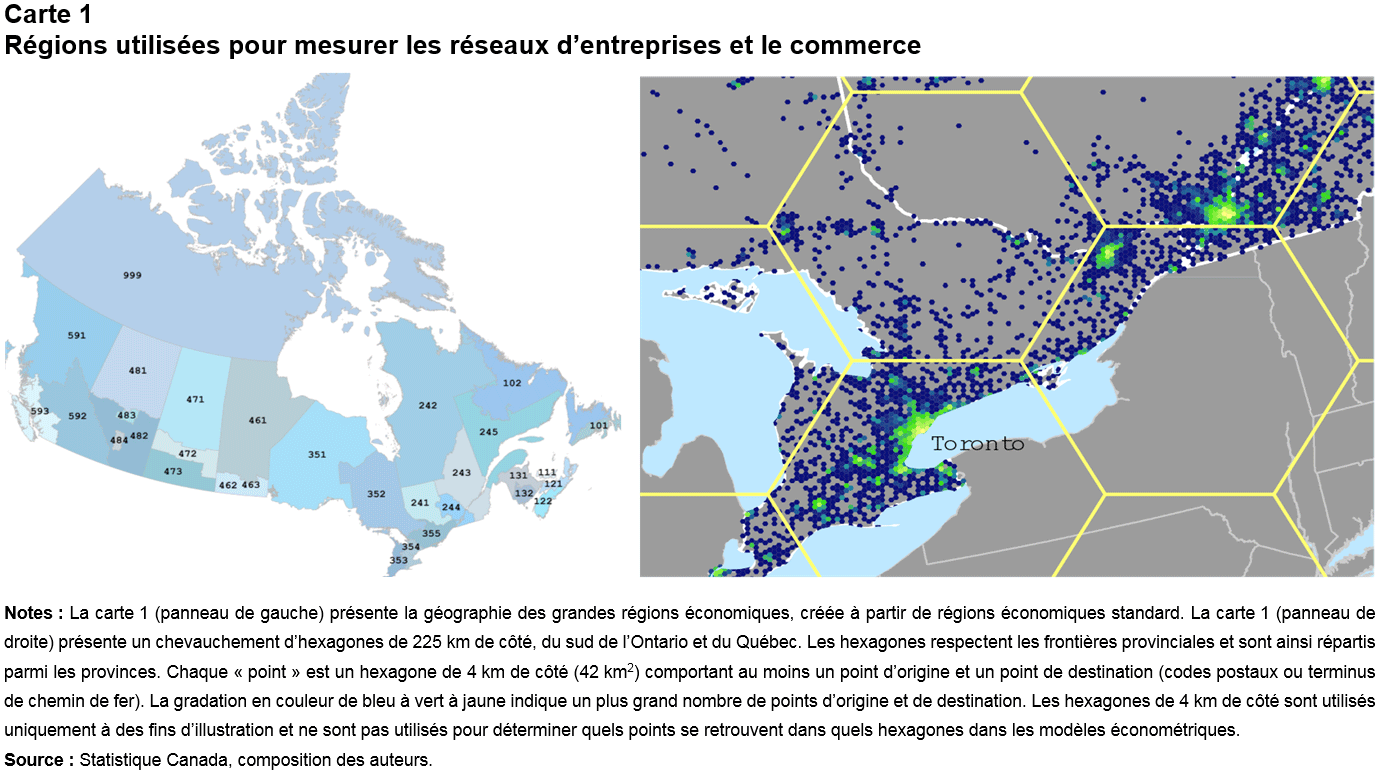
Description de la carte 1
Le titre de la carte 1 est « Régions utilisées pour mesurer les réseaux d’entreprises et le commerce ».
La carte 1 comporte deux panneaux (gauche et droit).
La carte 1 (panneau de gauche) est une carte des grandes régions économiques du Canada, lesquelles sont présentées dans diverses nuances de couleurs et identifiées avec des nombres à trois chiffres (à des fins d’illustration).
La carte 1 (panneau de droite) représente la densité des emplacements dans le Fichier des transports terrestres ainsi que les grilles hexagonales qui composent les unités géographiques dans le document. Elle couvre le sud de l’Ontario et une partie du Québec. L’emplacement de Toronto est indiqué sur la carte.
Les notes ci-dessous se rapportant à la figure comportent plus de renseignements.
Notes : La carte 1 (panneau de gauche) présente la géographie des grandes régions économiques, créée à partir de régions économiques standard. La carte 1 (panneau de droite) présente un chevauchement d’hexagones de 225 km de côté, du sud de l’Ontario et du Québec. Les hexagones respectent les frontières provinciales et sont ainsi répartis parmi les provinces. Chaque « point » est un hexagone de 4 km de côté (42 km2) comportant au moins un point d’origine et un point de destination (codes postaux ou terminus de chemin de fer). La gradation en couleur de bleu à vert à jaune indique un plus grand nombre de points d’origine et de destination. Les hexagones de 4 km de côté sont utilisés uniquement à des fins d’illustration et ne sont pas utilisés pour déterminer quels points se retrouvent dans quels hexagones dans les modèles économétriques.
La source de la carte 1 est « Statistique Canada, composition des auteurs ».
Pour obtenir de plus amples renseignements, veuillez communiquer avec Statistique Canada à STATCAN.infostats-infostats.STATCAN@canada.ca.
À cette fin, les flux des échanges entre les points d’origine et de destination sont mesurés à ces différentes unités géographiques. De manière similaire, il était possible de mesurer les réseaux d’entreprises entre les différents niveaux de géographie comme le résultat de la disponibilité des données géocodées sur les codes postaux dans le RE. Par conséquent, l’ensemble de données qui en découle mesure non seulement les flux des échanges entre une paire particulière de points d’origine et de destination, mais également le nombre d’emplacements d’exploitation au point d’origine qui appartiennent aux entreprises ayant des emplacements également au point de destination, de 2004 à 2012. De cette manière, l’étude peut également mesurer les réseaux d’entreprises à différents niveaux géographiques.
Les données sont limitées dans le sens qu’elles ne permettent pas d’identifier des entreprises qui font du commerce entre elles; c’est-à-dire que seules les régions peuvent être relevées. L’identification découle d’une variation des liens au sein des réseaux d’entreprises entre les paires de régions et au fil du temps. Toutefois, cette stratégie empirique peut permettre d’en apprendre beaucoup. Elle offre un moyen d’examiner si l’effet bien documenté des frontières sur le commerce est également présent dans les réseaux d’entreprises. Ces données servent également à évaluer si les réseaux sont importants pour le commerce entre les régions et s’ils tiennent lieu de complément ou de substitut globalement et selon le secteur d’industrie. Quoique l’âge de ces données peut être perçu comme une limite, il est peu probable que la relation de base sous-jacente entre les réseaux d’entreprises, le commerce et les effets des frontières provinciales change beaucoup au cours du temps. Par exemple, il a été démontré que les effets mêmes des frontières provinciales sont très persistants, sans tendance à la baisse ou à la hausse identifiable entre 2004 et 2012 (Bemrose, Brown et Tweedle, 2017).
À la section suivante (section 4), on commence l’analyse en examinant dans quelle mesure les réseaux d’entreprises sont touchés par la distance et les effets des frontières provinciales après avoir tenu compte de la taille relative des deux régions liées par des entreprises, par secteur. Cet examen est suivi d’une analyse des réseaux d’entreprises sur le commerce (section 5).
4 Analyse des réseaux d’entreprises
Il est bien établi, dans la littérature sur le commerce, que la distance et les frontières provinciales influent sur le niveau des échanges intraprovinciaux et interprovinciaux (ou régionaux) au Canada (Agnosteva, Anderson et Yotov, 2014; Bemrose, Brown et Tweedle, 2017; Albrecht et Tombe, 2016). De manière similaire, l’étude porte sur la facilité avec laquelle les réseaux d’entreprises traversent les frontières, toutes choses étant égales par ailleurs. Au départ, cela suppose l’élaboration d’un cadre empirique qui, bien que ne reposant pas sur des microfondations explicites, fournit certaines orientations essentielles sur la façon dont l’expansion spatiale des réseaux entre les régions peut être estimée.
4.1 Modèle de réseaux d’entreprises
Le modèle est fondé sur une prémisse contrefactuelle très simple. Autrement dit, si aucun coût n’est associé à la construction, l’achat et l’exploitation d’emplacements à diverses distances (c.-à-d. aucune prise en compte de la friction de distance), alors la probabilité prévue qu’un emplacement d’exploitation dans fasse partie d’une entreprise exerçant des activités dans doit être tributaire du nombre d’entreprises exerçant des activités dans () et de leur probabilité sous-jacente () d’être une entreprise à unités multiples. En retour, cela dépendra d’un vecteur () qui caractérise la population des entreprises dans (p. ex. leurs industries, leurs tailles et leurs structures de gestion). Par conséquent, la part prévue d’emplacements d’exploitation dans qui font partie d’une entreprise exerçant des activités dans devrait être tributaire de la part pondérée du () de de toutes les entreprises. En termes officiels, cela peut être exprimé comme
(3)
À partir de l’équation (3), la proportion d’emplacements d’exploitation à unités multiples ()Note 6 dans liés à , , par rapport à la prémisse contrefactuelle est définie comme
(4)
en supposant qu’il n’existe aucune friction de la distance dans l’espace, on s’attend à ce que = 1. Mais s’il existe un coût de développement pour les réseaux d’entreprises, alors on s’attendrait à ce que Note 7. La résolution (4) pour se traduit par :
(5)
laquelle peut être estimée par log-linéarisation et en tenant compte des inconnus , et . Cela est réalisé en définissant et en substituant les effets fixes pour et, pour simplifier les choses, pour . , lequel tient compte de la variation dans les coûts de gestion de réseaux d’un point à l’autre , est défini comme suit :
(6)
où est la distance entre et , et et sont des variables binaires interprovinciales et interrégionales, respectivement. Ainsi, la force des liens de réseau entre et est tributaire de la propension de à générer et à d’absorber des liens de réseau conditionnés sur les coûts associés à l’établissement et à l’exploitation d’unités selon la distance et les frontières. À l’instar de Head et Mayer (2014), nous avons utilisé un estimateur du pseudo maximum de vraisemblance de Poisson (Poisson-PML) pour évaluer l’équation ci-dessus dans une formule de section transversale :
(7)
où est un terme d’erreurs multiplicatif. Nous évaluons (7) dans les trois unités géographiques (c.-à-d. les provinces, les GRE et les grilles hexagonales [de 225 km de côté]) pour le secteur des entreprises dans son ensemble et chacun des secteurs. L’analyse commence au niveau provincial et passe ensuite au niveau infraprovincial.
4.2 Réseaux d’entreprises provinciaux
L’analyse au niveau provincial de l’agrégation se déroule initialement en établissant une description de base du modèle de connexions de réseau dans les provinces par secteur. Cela permet d’avoir une première compréhension intuitive des évaluations des modèles qui suivent quand l’équation (7) est estimée, produisant le premier test des hypothèses H1 et H2, à savoir que les réseaux d’entreprises se dissipent avec la distance et en traversant les frontières provinciales.
4.2.1 Décrire les réseaux d’entreprises
Pour commencer, il est utile d’examiner l’importance relative des entreprises à unités multiples au Canada. Le tableau 2 présente la structure des entreprises et la répartition par secteur des emplacements d’exploitation dans le secteur des entreprises. La plupart des emplacements d’exploitation dans le secteur des entreprises font partie d’entreprises à emplacement unique (90,9 %) plutôt que d’entreprises à unités multiples (9,1 %). Toutefois, les entreprises à unités multiples contribuent grandement à l’économie canadienne : elles constituent juste un peu plus de 40 % de tous les emploisNote 8. Le secteur des biens seulement est constitué principalement d’emplacements d’exploitation qui sont de nature simple (98,6 %), alors que le secteur des services seulement comprend plus d’emplacements qui appartiennent à des entreprises à unités multiples (8,8 %). Selon leur définition, tous les emplacements d’exploitation du secteur des biens hybrides appartiennent à des entreprises à unités multiples.
Comme l’analyse cherche à tester l’effet des frontières provinciales sur les réseaux d’entreprises, elle présente la part des emplacements à unités multiples qui font partie des entreprises ayant des emplacements dans au moins deux provinces. Dans l’ensemble, 69,3 % des emplacements d’exploitation appartenant à des entreprises à unités multiples dans le secteur des entreprises sont également à provinces multiples. Cela reflète grandement la part élevée des biens hybrides, où 85,2 % des emplacements d’exploitation sont à provinces multiples. Les parts du secteur des services seulement (65,7 %) et du secteur des biens seulement (33,3 %) sont un peu plus faibles.
| Secteur | Structure des entreprises | |||
|---|---|---|---|---|
| Total | Unique | Multiple | Plusieurs provinces | |
| pourcentage | ||||
| Biens seulement | 100,0 | 98,6 | 1,4 | 33,3 |
| Services seulement | 100,0 | 91,2 | 8,8 | 65,7 |
| Biens hybrides | 100,0 | Note ...: n'ayant pas lieu de figurer | 100,0 | 85,2 |
| Ensemble du secteur des entreprises | 100,0 | 90,9 | 9,1 | 69,3 |
|
... n'ayant pas lieu de figurer Notes : « Unique » fait référence à des emplacements qui appartiennent à des entreprises ayant un emplacement unique et « Multiple » fait référence à des emplacements qui appartiennent des entreprises ayant des emplacements multiples. Pour les entreprises à emplacements multiples, « Plusieurs provinces » est un sous-ensemble d’emplacements qui appartiennent à une entreprise ayant des emplacements dans plus d’une province. Source : Statistique Canada, calculs des auteurs. |
||||
L’intensité des liens de réseaux d’entreprises qui traversent les frontières provinciales peut être calculée en prenant le nombre d’emplacements d’exploitation dans la province liés à la province en proportion de de tous les emplacements d’exploitation d’entreprises à unités multiples : . Le nombre d’emplacements d’exploitation d’entreprises à unités multiples est utilisé pour normaliser ses liens extérieurs, car ceux-ci forment le bassin d’unités où les entreprises ont le potentiel d’avoir des liens avec d’autres provinces. Pour rendre cela concret, le tableau 3 présente des réseaux d’entreprises provinciaux pour l’Ontario, en utilisant la répartition par secteur décrite ci-dessus.
Pour l’ensemble du secteur des entreprises, un examen superficiel des parts donne à penser que les emplacements d’exploitation qui appartiennent à des entreprises à provinces multiples ont tendance à être concentrés près de la province d’exploitation. C’est-à-dire que la plupart des entreprises à unités multiples n’exercent pas d’activités à l’extérieur de la province. Quand elles en ont, on observe une tendance, bien qu’elle ne soit pas universelle, de leurs liens à se dissiper avec la distance. Par exemple, parmi tous les emplacements d’exploitation dans le secteur des entreprises en Ontario, 30,9 % appartiennent également à des entreprises ayant des activités au Québec. Ces liens se dissipent à mesure que l’on se déplace vers l’est, 22,8 % des emplacements en Ontario appartenant également à des entreprises au Nouveau-Brunswick, 24,3 %, à des entreprises en Nouvelle-Écosse, 14,7 %, à des entreprises à l’Île-du-Prince-Édouard et 18,8 %, à des entreprises à Terre-Neuve-et-Labrador. On retrouve des liens plus forts dans les provinces de l’Ouest, 30,9 % des emplacements en Ontario étant également liés à l’Alberta et à la Colombie-Britannique.
Ces résultats agrégés masquent certaines différences importantes dans des secteurs. Il convient de noter que le secteur des biens seulement est très concentré et comporte peu de liens traversant les frontières provinciales. Bien que le Québec demeure la province la plus liée à l’Ontario, seulement 13,1 % des emplacements d’exploitation en Ontario appartiennent à des entreprises qui ont également des activités au Québec. Ces liens diminuent rapidement avec la distance. À l’exception de l’Alberta et de la Colombie-Britannique, les autres parts provinciales demeurent bien en dessous de 5 %. Le secteur des services seulement montre une plus grande dispersion provinciale dans les réseaux d’entreprises que pour les biens. L’Ontario a plus de liens avec les provinces de l’Ouest que partout ailleurs dans ce secteur, juste un peu plus de 28 % des emplacements en Ontario étant liés à des emplacements en Alberta et en Colombie-Britannique. On observe également de forts liens avec le Québec comme auparavant (27,5 %), mais également avec le Nouveau-Brunswick (20,9 %) et la Nouvelle-Écosse (22,3 %). En dernier lieu, les réseaux d’entreprises provinciaux dans les biens hybrides tendent à se concentrer autour des provinces voisines, mais elles sont également dispersées dans tout le Canada. Notamment, 50,4 % des emplacements sont liés au Québec et 38,0 % au voisin à l’ouest de l’Ontario, soit le Manitoba.
| Secteur | Part de sa propre province : | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T.-N.-L. | Î.-P.-É. | N.-É. | N.-B. | Qc | Ont. | Man. | Sask. | Alb. | C.-B. | |
| pourcentage | ||||||||||
| Biens seulement | 2,3 | 1,0 | 3,5 | 3,2 | 13,1 | 100,0 | 4,4 | 3,1 | 9,3 | 9,2 |
| Services seulement | 17,3 | 14,4 | 22,3 | 20,9 | 27,5 | 100,0 | 24,9 | 21,8 | 28,3 | 28,5 |
| Biens hybrides | 28,2 | 18,6 | 37,3 | 35,3 | 50,4 | 100,0 | 38,0 | 34,6 | 47,0 | 45,9 |
| Ensemble du secteur des entreprises | 18,8 | 14,7 | 24,3 | 22,8 | 30,9 | 100,0 | 26,6 | 23,5 | 30,9 | 30,9 |
|
Notes : En prenant l’Ontario comme référence, chaque élément représente une partie de ces emplacements qui font partie de l’entreprise ayant des activités dans la province associée. Veuillez prendre note que les éléments ne totaliseront pas 100 % (totaux de sa propre province), car les liens sont asymétriques. Par définition,
et le total pour l’Ontario sera alors de 100 %. Source : Statistique Canada, calculs des auteurs. |
||||||||||
Comme l’exemple de l’Ontario le montre, les économies provinciales sont reliées par des liens d’entreprises. Les liens d’entreprises qui traversent les frontières provinciales sont plus susceptibles d’être établis avec des provinces voisines. Viennent ensuite les provinces comportant les plus grands marchés (p. ex. la Colombie-Britannique et l’Alberta dans l’exemple des réseaux d’entreprises de l’Ontario). Bien que l’analyse descriptive montre l’importance de la distance et des frontières provinciales dans les divers secteurs de l’industrie, il s’agit d’un test limité axé sur une province effectué sans contrôle de la capacité de la région de destination () à absorber les liens des réseaux. L’équation (5) porte à croire qu’une telle mesure est nécessaire.
4.2.2 Évaluations des modèles
Le tableau 4 présente les résultats de la régression au niveau provincial pour tous les secteurs. L’analyse est axée, en premier lieu, sur le secteur des entreprises (modèle 1). Les résultats montrent que les liens des réseaux d’entreprises baissent avec la distance et, que lorsqu’on traverse les frontières provinciales, la baisse résulte de l’effet des frontières provinciales. L’effet des frontières provinciales de 0,71 laisse entendre que les réseaux d’entreprises du secteur des entreprises sont probablement 29 % moins élevés entre les provinces qu’à l’intérieur de celles-ci. Ajouter un terme quadratique sur la distance pour tenir compte de ses effets non linéaires possibles se traduit par des évaluations négligeables de la distance et un effet de frontière légèrement plus fort. Comme la prochaine sous-section le démontrera, mesurer des réseaux dans des régions plus définies permet de mieux tester si la distance a un effet non linéaire sur la distance et si les effets des frontières sont sensibles aux unités géographiques choisies. Il a été démontré que c’était le cas de ce dernier élément quand on mesure les effets des frontières sur le commerce (p. ex. Hillberry et Hummels, 2008; Bemrose, Brown et Tweedle, 2017). Néanmoins, ces résultats constituent un test de base des deux premières hypothèses, qui révèle que la distance a un effet négatif sur les réseaux (H1) et que les frontières provinciales font de même (H2).
On s’attend à ce que les résultats changent, plus particulièrement en ce qui a trait à l’influence de la distance, quand ils sont désagrégés par secteur. Pour les producteurs de biens (biens hybrides ou biens seulement), on prévoit que les réseaux d’entreprises diminueront rapidement avec la distance pour les raisons invoquées ci-dessus (p. ex. le coût plus élevé d’organiser la production de biens sur de longues distances). Cela provient des données. L’effet de la distance a été beaucoup plus négatif pour les secteurs des biens hybrides et des biens seulement que pour le secteur des services. L’effet des frontières provinciales a été négatif pour les secteurs des biens hybrides et des biens seulement, mais significatif uniquement pour le secteur des biens seulement. Le secteur des services seulement, du fait qu’il constitue la plus grande partie du secteur des entreprises, a produit des résultats qui sont assez similaires.
| Secteur des entreprises | Biens hybrides | Biens seulement | Services seulement | |||||
|---|---|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,146Note ** | 0,407 | −0,211Note ** | 0,335 | −0,586Note ** | −0,777 | −0,114Note ** | 0,440 |
| Erreur-type | 0,0197 | 0,3740 | 0,0172 | 0,3380 | 0,0777 | 0,8580 | 0,0213 | 0,3880 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,0373 | Note ...: n'ayant pas lieu de figurer | −0,0368 | Note ...: n'ayant pas lieu de figurer | 0,0131 | Note ...: n'ayant pas lieu de figurer | −0,0373 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,0246 | Note ...: n'ayant pas lieu de figurer | 0,0224 | Note ...: n'ayant pas lieu de figurer | 0,0594 | Note ...: n'ayant pas lieu de figurer | 0,0255 |
| Interprovincial | ||||||||
| Coefficient | −0,347Note ** | −0,483Note ** | −0,00487 | −0,139 | −1,040Note ** | −0,998Note ** | −0,464Note ** | −0,600Note ** |
| Erreur-type | 0,0835 | 0,1440 | 0,0705 | 0,1200 | 0,1610 | 0,2420 | 0,0898 | 0,1530 |
| Constante | ||||||||
| Coefficient | 8,514Note ** | 6,609Note ** | 7,641Note ** | 5,765Note ** | 7,311Note ** | 7,971Note ** | 7,937Note ** | 6,032Note ** |
| Erreur-type | 0,138 | 1,290 | 0,133 | 1,166 | 0,584 | 2,915 | 0,144 | 1,343 |
| Observations (nombre) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Effet de frontière (valeur) | 0,71 | 0,62 | 1,00 | 0,87 | 0,35 | 0,37 | 0,63 | 0,55 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||||
4.3 Réseaux d’entreprises infraprovinciaux
Les tableaux 5-1 et 5-2 présentent les résultats de la régression pour des réseaux d’entreprises en utilisant des GRE et des hexagones de 225 km de côté. De manière intuitive, ces unités géographiques plus fines offrent un test plus robuste de l’effet des frontières provinciales sur les réseaux, car elles représentent mieux le modèle actuel de connexions des réseaux qui tend à être de plus petite taille, alors que les provinces, en particulier les plus grandes, tendent à obscurcir ces connexions, laissant peut-être les réseaux intraprovinciaux paraître plus forts qu’ils ne le sont en réalité. L’utilisation d’unités géographiques plus définies promet également d’offrir une perspective plus nuancée sur la manière dont les entreprises organisent leur production dans l’espace.
L’effet de mesurer les réseaux d’entreprises dans des unités géographiques infraprovinciales est de réduire sensiblement l’effet estimé des frontières, mais jamais de les éliminer complètement, peu importe l’unité géographique ou la spécification de modèle utilisée. En mettant l’accent sur le secteur des entreprises, pour les GRE, les réseaux interprovinciaux tendent à être environ 19 % plus faibles que les réseaux à l’intérieur des provinces. Ce résultat est invariant sur le plan qualitatif selon les deux unités géographiques et les spécifications de modèle. En ampleur, il est inférieur à l’effet des frontières estimé quand les provinces sont utilisées comme unités d’analyse, mais il demeure significatif sur le plan économique.
Parmi les trois secteurs (biens hybrides, biens seulement et services seulement), les effets des frontières provinciales tendent à être les plus faibles pour les biens hybrides et les plus forts pour les biens seulement, les services se retrouvant au milieu. Cela peut être observé plus facilement quand l’analyse porte sur les résultats en utilisant le terme quadratique de distance (modèle 2), lequel tend à offrir continuellement le plus faible effet de frontières pour les biens. Les raisons pour lesquelles il en est ainsi laissent place à l’interprétation. Une hypothèse raisonnable est que, lorsque le coût d’acquisition ou de construction de nouveaux emplacements d’exploitation hors des frontières provinciales est fixe (p. ex. l’adaptation à un des systèmes de réglementation différents), les plus grandes entreprises sont peut-être mieux en mesure d’amortir ces coûts sur un volume plus important de ventes. Par conséquent, si on considère les biens hybrides comme étant les plus importants parmi les secteurs, les résultats seront cohérents avec cette interprétation. Toutefois, il reste encore du travail à accomplir pour tester ces hypothèses plus en profondeur.
Comme il est mentionné plus tôt, les entreprises produisant des biens sont incitées à maintenir la production à proximité, alors que les fournisseurs de services pourraient être plus enclins à rechercher de nouveaux marchés. Comme le montre le modèle 1, la distance présente l’effet le plus négatif sur les réseaux pour les secteurs des biens seulement et des biens hybrides par rapport au secteur des services seulement. Cela est valable, peu importe l’unité géographique choisie. En outre, pour les producteurs de biens, les réseaux interrégionaux sont beaucoup plus faibles que les réseaux intrarégionaux, alors que cela n’est pas le cas, en termes relatifs, pour le secteur des biens hybrides ou le secteur des services seulement. Cette constatation concorde avec l’hypothèse selon laquelle seuls les producteurs de biens construiraient des installations sur de plus longues distances dans le but de pénétrer de nouveaux marchés. On constate cela dans le secteur des biens seulement et sur le plan de la mesure des réseaux à l’aide de l’unité géographique hexagonale. Ici, le terme quadratique sur la distance est positif, mais faiblement significatif.
En dernier lieu, ces estimations sont reprises au moyen d’une mesure des réseaux pondérée par le nombre d’emplois qui tient compte de la taille des emplacements d’exploitation pour le secteur des entreprises en utilisant l’unité géographique hexagonale. Il en a résulté des estimations qualitativement semblables (voir le tableau 9 en annexe).
| Secteur des entreprises | Biens hybrides | Biens seulement | Services seulement | |||||
|---|---|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,131Note ** | 0,4420Note ** | −0,198Note ** | 0,5150Note ** | −0,392Note ** | 1,5180Note ** | −0,0996Note ** | 0,4070Note ** |
| Erreur-type | 0,00899 | 0,09110 | 0,00860 | 0,07190 | 0,06090 | 0,27400 | 0,00941 | 0,10300 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,0400Note ** | Note ...: n'ayant pas lieu de figurer | −0,0498Note ** | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | −0,0353Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,00621 | Note ...: n'ayant pas lieu de figurer | 0,00493 | Note ...: n'ayant pas lieu de figurer | 0,02060 | Note ...: n'ayant pas lieu de figurer | 0,00698 |
| Interprovincial | ||||||||
| Coefficient | −0,206Note ** | −0,240Note ** | −0,0768Note ** | −0,119Note ** | −0,707Note ** | −0,674Note ** | −0,258Note ** | −0,289Note ** |
| Erreur-type | 0,0246 | 0,0260 | 0,0207 | 0,0191 | 0,1160 | 0,0974 | 0,0280 | 0,0301 |
| Interrégional | ||||||||
| Coefficient | −0,235Note ** | −0,493Note ** | 0,00469 | −0,319Note ** | −1,046Note ** | −1,770Note ** | −0,301Note ** | −0,530Note ** |
| Erreur-type | 0,0497 | 0,0632 | 0,0476 | 0,0468 | 0,1230 | 0,1540 | 0,0518 | 0,0711 |
| Constante | ||||||||
| Coefficient | 7,919Note ** | 6,197Note ** | 6,916Note ** | 4,777Note ** | 5,683Note ** | −0,173 | 7,406Note ** | 5,880Note ** |
| Erreur-type | 0,0709 | 0,2780 | 0,0749 | 0,2240 | 0,3790 | 0,8700 | 0,0720 | 0,3130 |
| Observations (nombre) | 900 | 900 | 900 | 900 | 900 | 900 | 900 | 900 |
| Effet de frontière (valeur) | 0,81 | 0,79 | 0,93 | 0,89 | 0,49 | 0,51 | 0,77 | 0,75 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||||
| Secteur des entreprises | Biens hybrides | Biens seulement | Services seulement | |||||
|---|---|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,154Note ** | −0,107 | −0,214Note ** | 0,126Tableau 5-2 Note † | −0,617Note ** | −1,224Note ** | −0,121Note ** | −0,184Note * |
| Erreur-type | 0,00664 | 0,08440 | 0,00598 | 0,07070 | 0,05570 | 0,32500 | 0,00736 | 0,09220 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,00320 | Note ...: n'ayant pas lieu de figurer | −0,0235Note ** | Note ...: n'ayant pas lieu de figurer | 0,0445Tableau 5-2 Note † | Note ...: n'ayant pas lieu de figurer | 0,00434 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,00581 | Note ...: n'ayant pas lieu de figurer | 0,0049 | Note ...: n'ayant pas lieu de figurer | 0,0241 | Note ...: n'ayant pas lieu de figurer | 0,00634 |
| Interprovincial | ||||||||
| Coefficient | −0,218Note ** | −0,220Note ** | −0,100Note ** | −0,117Note ** | −0,507Note ** | −0,508Note ** | −0,271Note ** | −0,268Note ** |
| Erreur-type | 0,0181 | 0,0186 | 0,0144 | 0,0142 | 0,0824 | 0,0844 | 0,0217 | 0,0222 |
| Interrégional | ||||||||
| Coefficient | −0,177Note ** | −0,197Note ** | 0,0583 | −0,0901Tableau 5-2 Note † | −0,734Note ** | −0,517Note ** | −0,247Note ** | −0,220Note ** |
| Erreur-type | 0,0442 | 0,0561 | 0,0421 | 0,0506 | 0,1160 | 0,1580 | 0,0457 | 0,0586 |
| Constante | ||||||||
| Coefficient | 4,094Note ** | 3,954Note ** | 3,128Note ** | 2,104Note ** | 1,666Note * | 3,425Note ** | 3,545Note ** | 3,735Note ** |
| Erreur-type | 0,0859 | 0,2700 | 0,1230 | 0,2360 | 0,7050 | 1,1260 | 0,0858 | 0,2950 |
| Observations (nombre) | 7 306 | 7 306 | 7 306 | 7 306 | 7 306 | 7 306 | 7 306 | 7 306 |
| Effet de frontière (valeur) | 0,80 | 0,80 | 0,90 | 0,89 | 0,60 | 0,60 | 0,76 | 0,76 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||||
5 Réseaux d’entreprises et commerce
L’étude se tourne maintenant vers le cœur de l’analyse et soulève deux questions connexes. En premier lieu, quelles sont l’ampleur et la direction de l’influence des réseaux d’entreprises sur le commerce interrégional? En d’autres mots, si les réseaux sont importants, agissent-ils comme un complément ou comme un substitut au commerce? En second lieu, quelles sont l’ampleur et la direction de l’effet des réseaux d’entreprises sur le commerce conditionnel aux coûts du commerce, si ces coûts sont associés à la distance ou aux frontières provinciales? Comme il est mentionné dans l’introduction, on suppose que, avec des coûts du commerce croissants associés à la distance et aux frontières, les économies de coûts que représente pour les entreprises le maintien des chaînes d’approvisionnement existantes (qu’elles soient internes ou externes à l’entreprise) peuvent être épuisées, ce qui incite les entreprises à rechercher de nouveaux fournisseurs plus près. Ainsi, on s’attend à ce que, étant donné que les distances sont plus longues entre les régions et les frontières, l’effet des réseaux d’entreprises sur le commerce passe de positif (un effet complémentaire) à négatif (un effet de substitution).
Sur le plan économétrique, l’étude permet d’aborder ce point en deux étapes. La première étape maintient l’approche transversale utilisée ci-dessus. Cela offre un test de base de la relation entre les réseaux et le commerce, mais il s’agit d’un test qui peut être endogène (p. ex. à la suite d’un biais causé par une variable manquante). Dans la seconde étape, on aborde ce point en établissant un panel de régions et en utilisant un estimateur par différence première.
5.1 Estimations transversales
Comme c’est maintenant la norme dans la littérature, un modèle de commerce évalué tient compte de la capacité des unités géographiques à générer et à absorber un commerce et d’une mesure des coûts du commerce entre elles. On définit ce modèle comme suit :
(8)
où est la valeur des expéditions de biens entre les régions et , et où et tiennent compte de la sortie et du potentiel de marché de et de la taille et du niveau de concurrence de , respectivement. Les coûts du commerce () sont pris en compte en fonction de la distance entre et () et d’un ensemble de variables binaires qui tiennent compte des effets des échanges intraprovinciaux () et intrarégionaux ().
(9)
Comme on s’attend également à ce que les réseaux d’entreprises réduisent les coûts du commerce, leur mesure bilatérale () est également incluse avec les autres mesures des coûts du commerce. L’analyse vérifie l’effet des réseaux d’entreprises dans le secteur des entreprises sur le commerce.
Pour en savoir davantage sur la construction et l’analyse en utilisant la mesure multiplicative des réseaux d’entreprises, veuillez consulter l’annexe.
Le modèle est estimé pour les hexagones de 225 km de côté (tableau 6). Le modèle de référence, lequel exclut les réseaux, est le modèle 1. Comme prévu, ce modèle montre que la distance présente un fort effet négatif sur le commerce. De plus, l’effet des frontières provinciales sur le commerce est négatif et indique que le commerce interprovincial correspond à environ 59 % du niveau du commerce intraprovincial, toutes choses étant égales par ailleurs. Bien qu’un modèle plus parcimonieux soit utilisé ici, ce résultat est qualitativement semblable aux résultats de Bemrose, Brown et Tweedle (2017).
Le modèle 2 comprend la mesure additive des réseaux d’entreprises du secteur des entreprises. L’effet des réseaux d’entreprises sur le commerce est positif. Cela donne à penser, au moins sur la base des données transversales, que les réseaux d’entreprises dans l’ensemble tendent à compléter le commerce, plutôt qu’à se substituer à celui-ci. Toutefois, leur inclusion réduit d’environ de moitié l’effet des frontières provinciales sur le commerce.
| Modèle 1 | Modèle 2 | |
|---|---|---|
| Coefficient | −0,828Note ** | −0,792Note ** |
| Erreur-type | 0,0635 | 0,0673 |
| Interprovincial | ||
| Coefficient | −0,466Note ** | −0,236Note * |
| Erreur-type | 0,0875 | 0,1010 |
| Interrégional | ||
| Coefficient | 0,1200 | 0,0948 |
| Erreur-type | 0,1280 | 0,1300 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | 0,585Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,111 |
| Constante | ||
| Coefficient | 17,13Note ** | 14,10Note ** |
| Erreur-type | 0,763 | −1,031 |
| Observations (nombre) | 7 306 | 7 189 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||
5.2 Estimations d’après le panel
Comme il est mentionné ci-dessus, en raison d’un biais causé par une variable manquante et d’une causalité inverse, les estimations transversales peuvent être endogènes par rapport à la mesure des réseaux. Une causalité inverse peut constituer un sujet de préoccupation, car un commerce croissant pourrait inciter les entreprises à construire des emplacements d’exploitation dans ces nouveaux marchés. Toutefois, à ce jour, la plus grande partie des données empiriques et théoriques donnent à penser que les flux d’échanges suivent l’expansion des réseaux, c’est-à-dire que les entreprises utilisent leurs contacts (c.-à-d. leur réseau) pour découvrir de nouveaux marchés (Chaney, 2014). À partir de là, la causalité inverse ne semble pas représenter une source importante de biais. Des biais causés par une variable manquante peuvent provenir de différences inexpliquées dans la structure de l’industrie. En supposant que ceux-ci sont fixes sur de courtes périodes, une première différenciation permet également à l’étude de tester en outre l’effet des coûts du commerce sur les réseaux d’entreprises. Comme les coûts du commerce augmentent, on s’attend à ce que l’effet des réseaux sur le commerce passera du commerce complémentaire (positif) au commerce de substitution (négatif). Le test pour cet aspect permet de vérifier les hypothèses H3 et H4. Comme on prévoit que les coûts du commerce seront directement proportionnels à la distance et aux frontières provinciales, l’analyse détermine l’effet de la croissance des réseaux () sur la croissance du commerce en utilisant la distance entre les régions () et en examinant si le flux traverse les frontières provinciales (). Officiellement, on définit ce modèle comme suit :
(10)
le niveau différé de commerce () étant compris afin d’intégrer la régression à la moyenne. Pour réduire l’effet de bruit dans les données, dans l’étude, le panel de neuf ans est divisé en trois sous-périodes (), soit 2004 à 2006, 2007 à 2009 et 2010 à 2012, et la moyenne des variables est calculée au cours des années de chaque périodeNote 9. En dernier lieu, les effets fixes par période () sont inclus pour tenir compte de l’inflation et des macrochocs. Les périodes sont ensuite différenciées pour obtenir (10), lequel est estimé en utilisant les moindres carrés ordinaires (MCO).
Sur le plan des résultats, l’analyse commence par une estimation de l’effet des réseaux d’entreprises du secteur des entreprises (biens et services) sur le commerce dans deux unités géographiques, dans les GRE et dans les hexagones de 225 km de côté, présentée dans les tableaux 7-1 et 7-2. L’incidence des réseaux d’entreprises dans le secteur des entreprises sur le commerce est négatif et significatif seulement pour les GRE (voir le tableau 7-1, modèle 1). La relation entre les réseaux et le commerce est beaucoup plus claire quand son effet est conditionné sur la distance et les frontières provinciales. En ce qui concerne les résultats pour le secteur des entreprises pour les GRE, l’effet des réseaux d’entreprises sur le commerce est positifNote 10. Toutefois, leur effet chute avec la distance et les frontières provinciales (voir le tableau 7-1, modèle 2). Cela vaut également pour les secteurs (biens hybrides, biens seulement et services seulement) parmi les deux unités géographiques, bien que parfois, l’effet est plus faible, plus particulièrement en ce qui concerne les effets des réseaux d’entreprises de biens seulement. En utilisant les résultats pour les GRE, à tout juste plus de 3 300 km, l’effet des réseaux d’entreprises du secteur des entreprises sur le commerce se révèle négatif, passant de complément à substitut pour le commerceNote 11. C’est un peu moins que la distance de conduite de Toronto à Calgary. Ce résultat suppose évidemment que le commerce doit traverser des frontières provinciales. L’effet de conditionnement des frontières provinciales sur l’influence des réseaux sur le commerce est également négatif et significatif pour les deux unités géographiques. Selon des estimations pour les GRE, si les flux des échanges traversent une frontière provinciale, l’effet des réseaux d’entreprises sur le commerce se révèle négatif à juste au-dessus de 1 200 km. Ainsi, si l’on s’inspire d’Engel et Rogers (1996), l’effet des frontières provinciales est équivalent à l’ajout de 2 100 km au trajet entre des provinces. Un trajet sur cette distance engagerait un coût de transport ad valorem d’environ 5,7 % (Behrens et Brown, 2018). Cela signifie que, pour de nombreuses paires importantes de régions interprovinciales (p. ex. Ontario-Alberta), l’effet des réseaux d’entreprises sur le commerce est négatif. Ces résultats correspondent aux hypothèses H3 et H4. Autrement dit, comme les coûts du commerce augmentent en raison de la distance et des frontières, les réseaux d’entreprises passent d’un état de complément à un état de substitut pour les flux des échanges, alors que la production (H3) et l’approvisionnement des entrants (c.-à-d. les chaînes d’approvisionnement) (H4) se déplacent vers la destination.
| Secteur des entreprises | Biens hybrides | Biens seulement | Services seulement | |||||
|---|---|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,300Note ** | −0,420Note ** | −0,278Note ** | −0,332Note ** | −0,196Note ** | −0,223Note ** | −0,310Note ** | −0,408Note ** |
| Erreur-type | 0,0444 | 0,0527 | 0,0425 | 0,0475 | 0,0304 | 0,0328 | 0,0450 | 0,0516 |
| Coefficient | −5,263Note ** | 35,350Note ** | 0,145 | 16,580Note ** | −0,156Tableau 7-1 Note † | 2,138Note ** | −4,284Note ** | 31,740Note ** |
| Erreur-type | 1,2600 | 5,0140 | 0,5000 | 3,0210 | 0,0817 | 0,4960 | 1,2610 | 4,9230 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −4,467Note ** | Note ...: n'ayant pas lieu de figurer | −1,761Note * | Note ...: n'ayant pas lieu de figurer | −0,355Tableau 7-1 Note † | Note ...: n'ayant pas lieu de figurer | −4,293Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 1,213 | Note ...: n'ayant pas lieu de figurer | 0,743 | Note ...: n'ayant pas lieu de figurer | 0,182 | Note ...: n'ayant pas lieu de figurer | 1,188 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −4,363Note ** | Note ...: n'ayant pas lieu de figurer | −1,923Note ** | Note ...: n'ayant pas lieu de figurer | −0,256Note ** | Note ...: n'ayant pas lieu de figurer | −3,733Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,582 | Note ...: n'ayant pas lieu de figurer | 0,396 | Note ...: n'ayant pas lieu de figurer | 0,066 | Note ...: n'ayant pas lieu de figurer | 0,559 |
| Observations (nombre) | 1 740 | 1 740 | 1 740 | 1 740 | 1 206 | 1 206 | 1 740 | 1 740 |
| R au carré | 0,190 | 0,245 | 0,173 | 0,199 | 0,176 | 0,194 | 0,194 | 0,237 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||||
| Secteur des entreprises | Biens hybrides | Biens seulement | Services seulement | |||||
|---|---|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,349Note ** | −0,372Note ** | −0,353Note ** | −0,367Note ** | −0,235Note ** | −0,248Note ** | −0,353Note ** | −0,379Note ** |
| Erreur-type | 0,0156 | 0,0177 | 0,0160 | 0,0166 | 0,0302 | 0,0305 | 0,0159 | 0,0177 |
| Coefficient | 0,077 | 10,400Note ** | 0,772Note ** | 6,615Note ** | −0,204Note ** | 1,089Note * | −0,474 | 9,856Note ** |
| Erreur-type | 0,3440 | 3,9270 | 0,2690 | 1,5650 | 0,0673 | 0,4830 | 0,3060 | 2,9270 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −1,644Note * | Note ...: n'ayant pas lieu de figurer | −0,984Tableau 7-2 Note † | Note ...: n'ayant pas lieu de figurer | −0,324 | Note ...: n'ayant pas lieu de figurer | −1,994Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,663 | Note ...: n'ayant pas lieu de figurer | 0,563 | Note ...: n'ayant pas lieu de figurer | 0,226 | Note ...: n'ayant pas lieu de figurer | 0,678 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −1,256Note * | Note ...: n'ayant pas lieu de figurer | −0,670Note ** | Note ...: n'ayant pas lieu de figurer | −0,143Tableau 7-2 Note † | Note ...: n'ayant pas lieu de figurer | −1,221Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,5400 | Note ...: n'ayant pas lieu de figurer | 0,2360 | Note ...: n'ayant pas lieu de figurer | 0,0816 | Note ...: n'ayant pas lieu de figurer | 0,4040 |
| Observations (nombre) | 5 389 | 5 389 | 5 241 | 5 241 | 1 736 | 1 736 | 5 337 | 5 337 |
| R au carré | 0,210 | 0,223 | 0,209 | 0,213 | 0,179 | 0,187 | 0,214 | 0,230 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||||
6 Conclusions
Cet article offre une vue d’ensemble des réseaux d’entreprises et des structures des échanges intraprovinciales et interprovinciales au Canada. Les distances et les frontières influencent négativement les réseaux d’entreprises ainsi que les flux des échanges. On le voit dans les statistiques descriptives et peut-être davantage dans leurs effets estimés. Ces structures correspondent aux coûts plus élevés associés à la gestion d’unités d’exploitation sur des distances plus grandes et à l’établissement d’activités dans une autre province. À leur tour, les réseaux d’entreprises tendent à être associés de manière positive avec les flux des échanges, c’est-à-dire qu’ils agissent comme un complément au commerce. Toutefois, l’effet des réseaux d’entreprises sur le commerce est conditionnel aux variables associées à des coûts du commerce plus élevés. Notamment, étant donné une distance croissante et l’existence de frontières provinciales, l’effet de complémentarité des réseaux d’entreprises sur le commerce diminue. En outre, à des distances suffisamment longues et quand le commerce traverse des frontières, les réseaux passent plutôt d’un état de complément à un état de substitut pour le commerce. Ainsi, les frontières provinciales semblent réduire le degré auquel la cohésion de l’économie est assurée par des réseaux d’entreprises et le degré auquel ces réseaux peuvent faciliter le commerce. En fait, selon l’étude, après avoir tenu compte des réseaux d’entreprises, le coefficient de l’effet estimé des frontières provinciales chute de moitié.
Bien entendu, de nombreux ajouts peuvent être faits à cette analyse. À l’aide de tableaux d’entrées-sorties, il est possible de définir si les unités d’exploitation liées sont en aval ou en amont, ce qui fournit une meilleure mesure du degré auquel le commerce reflète ces relations fonctionnelles. Toutefois, l’étape suivante ultime consisterait à passer des mesures des réseaux et des flux parmi des régions agrégées, par lesquelles l’effet pur du commerce intra-entreprise est obscurci, à une base de données dans laquelle les expéditions intra-entreprises et interentreprises sont mesurées. À l’aide de renseignements détaillés sur l’emplacement où les envois sont ramassés et livrés, combinés à des renseignements sur l’emplacement et l’industrie des unités dans le Registre des entreprises, et d’autres sources, il serait possible de construire une telle base de données. L’analyse sera élargie lorsque des données plus récentes seront disponibles. Toutefois, parce que les relations relevées sont très persistantes, les résultats dont on a discuté dans la présente étude ne sont pas susceptibles de varier au cours du temps. Il s’agit d’une étape qui sera entreprise lorsque l’occasion se présentera.
7 Annexe
7.1 Fichier sur les transports de surface
Les données sur le commerce figurent dans le Fichier sur les transports de surface (FTS) de Statistique Canada. Le FTS combine des données de l’Enquête sur l’origine et la destination des marchandises transportées par camion et des lettres de transport ferroviaire pour les années 2002 à 2012. En outre, il offre des estimations sur la valeur du commerce des biens entre des régions au Canada et entre le Canada et les États-Unis. Fait à noter, il exclut les biens transportés par air, par pipeline et par eau.
Le FTS fournit également des données sur la distance des réseaux, c’est-à-dire la distance réelle parcourue pour un envoi de biens. Cela donne une mesure plus précise de la distance parcourue par les biens à l’intérieur des régions et entre les régions au Canada. Pour le présent document, la distance des réseaux est disponible pour l’échantillon au complet jusqu’aux paires de grandes régions économiques. Pour les hexagones de 225 km de côté, on retrouve des paires d’hexagones ayant des données manquantes sur la distance des réseaux. Dans ces cas, la distance orthodromique, une mesure couramment utilisée dans la littérature, est convertie en une distance de réseaux en utilisant un modèle. On réalise cela en effectuant une régression de la distance des réseaux sur un polynôme de la distance orthodromique et en utilisant des valeurs prédites pour les données manquantes. Pour les paires propres aux hexagones, la distance orthodromique à l’intérieur de l’hexagone est mesurée en tant que rayon d’un cercle d’une surface égale à celle de l’hexagone. Une description détaillée du FTS et de son élaboration est fournie dans l’article de Bemrose, Brown et Tweedle (2017).
7.2 Autres résultats
D’autres options de mesure des réseaux utilisées sont présentées dans l’étude. Une mesure fondée sur la définition mathématique d’un réseau (ou diagramme), que certains lecteurs connaissent peut-être mieux, est exposée ici. Souvenez-vous que l’objectif de la présente étude est de décrire les réseaux d’entreprises dans les régions, puis d’examiner la façon dont ces réseaux d’entreprises peuvent faciliter le commerce.
Prenons le réseau d’une entreprise , , dans lequel les nœuds, , sont des emplacements d’exploitation. Nous ne connaissons rien des relations entre les emplacements d’exploitation sinon qu’ils sont gérés par la même entreprise. On suppose que le réseau est complet, ce qui signifie qu’il y a des arêtes entre chaque paire de nœuds et dans .
Le diagramme des réseaux d’entreprises au niveau de l’économie dans son ensemble est l’union de tous les réseaux d’entreprises individuels,
(A1)
Pour ce qui est de l’effet des réseaux sur le commerce, l’échange se produit au niveau régional, entre des entreprises et à l’intérieur de celles-ci. Il est donc logique de traduire le diagramme en un diagramme régional dans lequel les nœuds sont des régions et les arêtes sont pondérées pour refléter la densité des connexions des entreprises dans le sous-jacent entre les paires de régions.
Le réseau régional est maintenant , dans lequel correspond à des régions, lesquelles peuvent être des provinces, des régions économiques ou d’autres unités géographiques. Le problème consiste alors à traduire la série d’ensembles d’arêtes d’entreprises () dans l’ensemble d’arêtes régionales ( ). Il existe peu d’options pour réaliser cette opération, alors qu’il convient de noter que le but est de représenter ce que le réseau d’entreprises signifie pour le commerce de biens.
L’idée de base est d’additionner les arêtes dans l’ensemble des régions à l’intérieur de chaque entreprise, puis d’agréger les données dans l’ensemble des entreprises dans l’économie. Cela donne un poids des arêtes dans le réseau régional de
(A2)
où est une entreprise, et sont des emplacements et et sont des régions. Dans le cas le plus simple, chaque arête d’entreprise a un poids 1. Pour s’harmoniser avec la notation utilisée dans le corps de l’article, écrire le nombre de nœuds dans un réseau comme , ce qui donne la mesure
(A3)
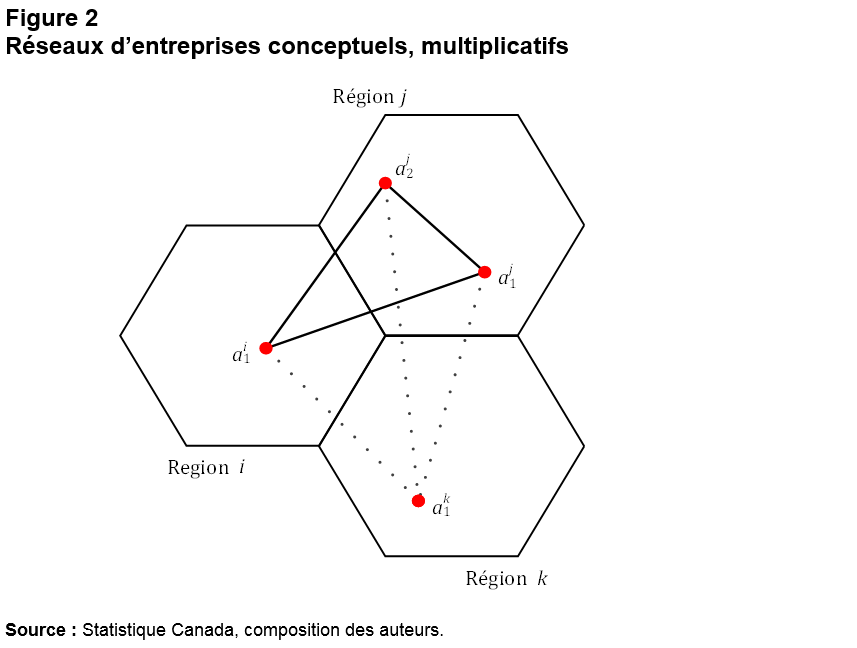
Description de la figure 2
Le titre de la figure 2 est « Réseaux d’entreprises conceptuels, multiplicatifs ».
Le diagramme illustre des liens possibles entre les emplacements d’une entreprise dans différentes régions.
On retrouve trois régions, représentées par des hexagones et portant les mentions « Région », « Région » et « Région ». Les hexagones sont contigus : ils sont joints sur deux côtés et sont représentés par une ligne noire.
L’entreprise a un emplacement dans la région , deux emplacements dans la région et un emplacement dans la région .
On observe des lignes pleines entre tous les emplacements dans les régions et , et des lignes pointillées de ces régions vers la région .
La source de la figure 2 est « Statistique Canada, composition des auteurs ».
Il s’ensuit que chaque emplacement doit diviser son attention entre les autres emplacements (sur le plan des biens, si un établissement échange avec les autres emplacements dans une entreprise, il doit diviser les biens physiques qu’il envoie entre les emplacements, en suivant un raisonnement semblables pour les intrants intermédiaires, le temps passé à communiquer et l’établissement de contacts). Prenons de nouveau une paire géographique : chaque emplacement dans est un partenaire d’échange potentiel pour tous les emplacements de l’entreprise dans . Comme on peut l’observer dans la figure 2, à l’intérieur d’une entreprise, on constate deux liens entre et . Toutefois, il existe également des liens dans la région . Dans ce cas, la force des liens bilatéraux de l’entreprise entre la région et est le nombre de liens potentiels entre et réduits par le nombre d’emplacements de l’entreprise dans toutes les régions. En termes mathématiques, cela se traduit par la pondération de chaque arête par le nombre total d’emplacements dans chaque entreprise, . Entrer ces poids dans les équations d’agrégation donne ce qui suit :
(A4)
Dans ce document, cette mesure est appelée , où est une mnémonique pour « multiplicative ». Cela correspond aux travaux de Combes, Lafourcade et Mayer (2005) et de Garmendia et coll. (2012). Toutefois, ces auteurs n’écartent pas la mesure des réseaux par le nombre d’unités dans l’entreprise, comme dans l’Équation (2).
Le nombre d’unités dans une entreprise donne une mesure directe de la taille de l’entreprise, mais celle-ci pourrait ne pas être complète. Par exemple, la question se pose facilement à savoir s’il est approprié de traiter des réseaux pour des dépanneurs et des supermarchés en utilisant le même nombre d’unités comme équivalents. Alors que les deux peuvent avoir les mêmes liens de réseau entre deux régions, les supermarchés sont probablement plus importants en ce qui a trait aux emplois. À leur tour, les emplois peuvent avoir des répercussions sur les flux des échanges, car les entreprises ont la capacité de générer plus de commerce interrégional. Dans la configuration d’un réseau, il est simple d’intégrer le poids des emplois dans le poids des arêtes des entreprises, en modifiant le poids de l’arête de à , dans lequel est le nombre d’emplois à l’emplacement de l’entreprise , et est le nombre total d’emplois dans l’entreprise . Par conséquent, l’analyse franchit l’étape supplémentaire de pondérer les comptes par le nombre d’emplois. Toutefois, lorsqu’on applique cela, aucune différence qualitative n’est observée dans les résultats.
7.2.1 Réseaux d’entreprises multiplicatifs
Les tableaux 8-1 et 8-2 présentent les résultats de l’association entre les réseaux d’entreprises multiplicatifs et les flux des échanges par les GRE et les hexagones de 225 km de côté en utilisant un modèle par panel de différence première. L’effet de la mesure des réseaux d’entreprises multiplicatifs est essentiellement négligeable. En ce qui concerne les résultats pour les GRE (tableau 8-1), les estimations sont significatives seulement pour les modèles entièrement précisés en utilisant des réseaux d’entreprises dans le secteur des biens hybrides. Les réseaux d’entreprises ont des répercussions positives sur les flux des échanges, mais le font à une échelle moindre pour les régions qui sont plus éloignées (comme le montre le coefficient négatif sur le paramètre d’interaction entre les réseaux d’entreprises et la distance). Cela correspond aux principales conclusions de la présente étude. Par ailleurs, contrairement à ce que montrent les résultats de l’étude, les réseaux d’entreprises interprovinciaux augmentent leurs effets principaux sur le commerce. Tous ces résultats ne sont plus valables quand les hexagones de 225 km de côté sont utilisés (tableau 8-2); dans ce cas, les résultats sont peu significatifs pour tous les modèles entièrement précisés.
7.2.2 Réseaux d’entreprises pondérés par le nombre d’emplois
Les trois mesures principales (, et ) utilisées dans cette étude sont élargies de façon à englober leurs versions pondérées par le nombre d’emplois. Plus particulièrement, l’équation (1) peut être redéfinie comme suit :
(A5)
où est le nombre d’emplois des emplacements d’exploitation de l’entreprise dans la région (qui possède également des emplacements dans la région ). De façon similaire, les équations (2) et (3) peuvent également être réécrites comme suit :
(A6)
Le mesure additive agrégée représente ainsi les liens de réseaux pondérés par le nombre d’emplois entre et . Il convient de noter que la mesure multiplicative, , est maintenant normalisée par le nombre total d’emplois de l’entreprise, . Les tableaux 9, 10 et 11 présentent de nouvelles estimations des principaux résultats reposant sur des réseaux d’entreprises du secteur des entreprises pondérés par le nombre d’emplois pour des hexagones de 225 km de côté. Tous les résultats sont valables. L’étendue des réseaux d’entreprises est influencée négativement par la distance et les frontières, l’inclusion de la mesure des réseaux d’entreprises réduisant l’effet des frontières provinciales d’environ de moitié, et l’influence positive des réseaux d’entreprises sur le commerce chute avec la distance lorsqu’on traverse des frontières.
| Secteur des entreprises | Biens hybrides | Biens seulement | Services seulement | |||||
|---|---|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,279Note ** | −0,279Note ** | −0,277Note ** | −0,285Note ** | −0,189Note ** | −0,189Note ** | −0,282Note ** | −0,282Note ** |
| Erreur-type | 0,0426 | 0,0428 | 0,0425 | 0,0425 | 0,0298 | 0,0298 | 0,0427 | 0,0429 |
| Coefficient | −0,117 | 0,1750 | −0,0180 | 2,1400Note * | 0,0039 | −0,394 | −0,335 | −0,115 |
| Erreur-type | 0,2870 | 1,8700 | 0,1550 | 0,9660 | 0,0413 | 0,3640 | 0,2490 | 1,4920 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | 0,4070 | Note ...: n'ayant pas lieu de figurer | 2,1630Note ** | Note ...: n'ayant pas lieu de figurer | −0,0527 | Note ...: n'ayant pas lieu de figurer | −0,888 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 1,185 | Note ...: n'ayant pas lieu de figurer | 0,587 | Note ...: n'ayant pas lieu de figurer | 0,171 | Note ...: n'ayant pas lieu de figurer | 0,908 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,0891 | Note ...: n'ayant pas lieu de figurer | −0,540Note ** | Note ...: n'ayant pas lieu de figurer | 0,0574 | Note ...: n'ayant pas lieu de figurer | 0,0826 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,3610 | Note ...: n'ayant pas lieu de figurer | 0,1870 | Note ...: n'ayant pas lieu de figurer | 0,0533 | Note ...: n'ayant pas lieu de figurer | 0,2920 |
| Observations (nombre) | 1 740 | 1 740 | 1 740 | 1 740 | 1 206 | 1 206 | 1 740 | 1 740 |
| R au carré | 0,173 | 0,173 | 0,173 | 0,181 | 0,172 | 0,173 | 0,175 | 0,176 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||||
| Secteur des entreprises | Biens hybrides | Biens seulement | Services seulement | |||||
|---|---|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,350Note ** | −0,350Note ** | −0,349Note ** | −0,349Note ** | −0,230Note ** | −0,230Note ** | −0,351Note ** | −0,351Note ** |
| Erreur-type | 0,0156 | 0,0156 | 0,0159 | 0,0159 | 0,0297 | 0,0297 | 0,0158 | 0,0158 |
| Coefficient | −0,156Note * | −0,837 | −0,118Note ** | −0,256 | −0,0500 | −0,0840 | −0,142Note * | −0,183 |
| Erreur-type | 0,0725 | 0,5560 | 0,0453 | 0,3060 | 0,0416 | 0,4060 | 0,0665 | 0,4300 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,0929 | Note ...: n'ayant pas lieu de figurer | 0,0951 | Note ...: n'ayant pas lieu de figurer | 0,1300 | Note ...: n'ayant pas lieu de figurer | 0,1040 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,224 | Note ...: n'ayant pas lieu de figurer | 0,11 | Note ...: n'ayant pas lieu de figurer | 0,182 | Note ...: n'ayant pas lieu de figurer | 0,178 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | 0,10300 | Note ...: n'ayant pas lieu de figurer | 0,00885 | Note ...: n'ayant pas lieu de figurer | −0,0101 | Note ...: n'ayant pas lieu de figurer | −0,00496 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,0895 | Note ...: n'ayant pas lieu de figurer | 0,0458 | Note ...: n'ayant pas lieu de figurer | 0,0672 | Note ...: n'ayant pas lieu de figurer | 0,0693 |
| Observations (nombre) | 5 389 | 5 389 | 5 241 | 5 241 | 1 736 | 1 736 | 5 337 | 5 337 |
| R au carré | 0,211 | 0,212 | 0,208 | 0,208 | 0,175 | 0,176 | 0,214 | 0,214 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||||
| Modèle 1 | Modèle 2 | |
|---|---|---|
| Coefficient | −0,154Note ** | −0,0582 |
| Erreur-type | 0,00757 | 0,09510 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,00667 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,00653 |
| Interprovincial | ||
| Coefficient | −0,165Note ** | −0,169Note ** |
| Erreur-type | 0,0198 | 0,0203 |
| Interrégional | ||
| Coefficient | −0,215Note ** | −0,257Note ** |
| Erreur-type | 0,0474 | 0,0571 |
| Constante | ||
| Coefficient | 7,205Note ** | 6,914Note ** |
| Erreur-type | 0,118 | 0,314 |
| Observations (nombre) | 7 306 | 7 306 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||
| Modèle 1 | Modèle 2 | Modèle 3 | |
|---|---|---|---|
| Coefficient | −0,828Note ** | −0,797Note ** | −0,513Note ** |
| Erreur-type | 0,0635 | 0,0659 | 0,0694 |
| Interprovincial | |||
| Coefficient | −0,466Note ** | −0,305Note ** | −0,142Note * |
| Erreur-type | 0,0875 | 0,0966 | 0,0687 |
| Interrégional | |||
| Coefficient | 0,1200 | 0,0777 | 3,9600Note ** |
| Erreur-type | 0,128 | 0,128 | 0,463 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | 0,442Note ** | Note ...: n'ayant pas lieu de figurer |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,075 | Note ...: n'ayant pas lieu de figurer |
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,339Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,0404 |
| Constante | |||
| Coefficient | 17,13Note ** | 13,44Note ** | 13,12Note ** |
| Erreur-type | 0,763 | 1,053 | 0,864 |
| Observations (nombre) | 7 306 | 7 189 | 7 189 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
|||
| Mesure additive () | Mesure multiplicative () | |||
|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Coefficient | −0,349Note ** | −0,380Note ** | −0,349Note ** | −0,349Note ** |
| Erreur-type | 0,0156 | 0,0168 | 0,0155 | 0,0156 |
| Coefficient | 0,2540 | 5,1190Note ** | −0,106Tableau 11 Note † | −0,0516 |
| Erreur-type | 0,1710 | 1,1030 | 0,0589 | 0,2320 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,924Note ** | Note ...: n'ayant pas lieu de figurer | −0,0474 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,301 | Note ...: n'ayant pas lieu de figurer | 0,172 |
| Coefficient | Note ...: n'ayant pas lieu de figurer | −0,612Note ** | Note ...: n'ayant pas lieu de figurer | −0,00289 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,1620 | Note ...: n'ayant pas lieu de figurer | 0,0447 |
| Constante | ||||
| Coefficient | 2,128Note ** | 2,643Note ** | 2,238Note ** | 2,243Note ** |
| Erreur-type | 0,747 | 0,753 | 0,746 | 0,746 |
| Observations (nombre) | 5 389 | 5 389 | 5 389 | 5 389 |
| R au carré | 0,211 | 0,228 | 0,222 | 0,211 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||
Bibliographie
Agnosteva, D.E., J.E. Anderson et Y.V. Yotov. 2014. Intra-national Trade Costs: Measurement and Aggregation. NBER Working Paper, no 19872. Cambridge, Massachusetts : National Bureau of Economic Research.
Albrecht, L., et T. Tombe. 2016. « Internal trade, productivity, and interconnected industries: A quantitative analysis ». Canadian Journal of Economics / Revue canadienne d’économique 49 (1) : 237 à 263.
Anderson, J.E. 2011. « The Gravity Model ». Annual Review of Economics 3 (1) : 133 à 160.
Anderson, J. E., et E. van Wincoop. 2004. « Trade Costs ». Journal of Economic Literature 42 (3) : 691 à 751.
Antràs, P. , 2003. « Firms, Contracts, and Trade Structure ». The Quarterly Journal of Economics 118 (4) : 1375 à 1418.
Antràs, P., et E. Helpman. 2004. « Global Sourcing ». Journal of Political Economy 112 (3) : 552 à 580.
Arbia, G. 1989. Spatial Data Configuration in Statistical Analysis of Regional Economic and Related Problems. Dordrecht : Kluwer Academic Publishers.
Atalay, E., A. Hortaçsu, J. Roberts et C. Syverson. 2011. « Network construction of production ». Proceedings of the National Academy of Sciences of the United States of America 108 (13) : 5199 à 5202.
Atalay, E., A. Hortaçsu et C. Syverson. 2014. « Vertical Integration and Input Flows ». American Economic Review 104 (4) : 1120 à 1148.
Baldwin, J.R., D. Beckstead et A. Girard. 2002. L’importance de l’entrée dans le secteur canadien de la fabrication : document accompagné d’une annexe sur les questions de mesure. Direction des études analytiques : documents de recherche, no 189. Produit no 11F0019M au catalogue de Statistique Canada. Ottawa : Statistique Canada.
Baldwin, J.R., et W.M. Brown. 2005. Multinationales étrangères et effectif des sièges sociaux des entreprises canadiennes de fabrication. Direction des études analytiques : documents de recherche, no 34. Produit no 11F0019M au catalogue de Statistique Canada. Ottawa : Statistique Canada.
Behrens, K., et W. M. Brown. 2018. « Transport Costs, Trade, and Geographic Concentration: Evidence from Canada ». Dans Handbook of International Trade and Transportation, publié sous la direction de B. Blonigen et W. Wilson, chapitre 6, p. 188 à 225. Cheltenham : Edward Elgar.
Behrens, K., et V. Sharunova. 2015. Inter- and intra-firm linkages: Evidence from microgeographic location patterns. CEPR Discussion Papers, no. DP 10921. Londres, Royaume-Uni : Centre for Economic Policy Research.
Belderbos, R., et L. Sleuwaegen. 1996. « Japanese Firms and the Decision to Invest Abroad: Business Groups and Regional Core Networks ». The Review of Economics and Statistics 78 (2) : 214.
Belderbos, R., et L. Sleuwaegen, 1998. « Tariff jumping DFI and export substitution: Japanese electronics firms in Europe ». International Journal of Industrial Organization 16 (5) : 601 à 638.
Bemrose, R.K., W.M. Brown et J. Tweedle. 2017. Parcourir tout le trajet : estimer l’effet des frontières provinciales sur le commerce lorsque l’unité géographique compte. Direction des études analytiques : documents de recherche, no 394. Produit no 11F0019M au catalogue de Statistique Canada. Ottawa : Statistique Canada.
Bernard, A.B., A. Moxnes et Y.U. Saito. 2015. Production Networks, Geography and Firm Performance. NBER Working Paper, no 21082. Cambridge, Massachusetts : National Bureau of Economic Research.
Brainard, S.L. 1997. « An empirical assessment of the proximity-concentration trade-off between multinational sales and trade ». The American Economic Review, 87 (4) : 520 à 544.
Caves, R.E. 1996. Multinational Enterprise and Economic Analysis. Cambridge : Cambridge University Press.
Chaney, T., 2008. « Distorted gravity: the intensive and extensive margins of international trade ». The American Economic Review 98 (4) : 1707 à 1721.
Chaney, T., 2014. « The network structure of international trade ». American Economic Review 104 (11) : 3600 à 3634.
Chaundy, D., 2016. Trade Barriers in Atlantic Canada: Opportunities for Regulatory Reform. Halifax : Conseil économique des provinces de l’Atlantique.
Combes, P. P., M. Lafourcade et T. Mayer. 2005. « The trade-creating effects of business and social networks: Evidence from France ». Journal of International Economics 66 (1) : 1 à 29.
Duranton, G., et D. Puga. 2005. « From sectoral to functional urban specialisation ». Journal of Urban Economics 57 (2) : 343 à 370.
Engel, C., et J.H. Rogers. 1996. « How Wide Is the Border? » The American Economic Review 86 (5) : 1112 à 1125.
Garmendia, A., C. Llano, A. Minondo et F. Requena. 2012. « Networks and the disappearance of the intranational home bias ». Economics Letters 116 (2) : 178 à 182.
Head, K., et T. Mayer. 2014. « Gravity Equations: Workhorse, Toolkit, and Cookbook ». Dans Handbook of International Economics, publié sous la direction de R.W. Jones, P.B. Kenen, G.M. Grossmann et K. Rogoff, 4 (3) : p. 131 à 195. Oxford, Royaume-Uni et Amsterdam : Elsevier.
Head, K., J. Ries et B.J. Spencer. 2004. « Vertical Networks and US Auto Parts Exports: Is Japan Different? » Journal of Economics & Management Strategy 13 (604) : 37 à 67.
Helliwell, J.F. 1998. How Much Do National Borders Matter? Washington, D.C. : The Brookings Institution.
Hillberry, R., et D. Hummels. 2008. « Trade responses to geographic frictions: A decomposition using micro-data ». European Economic Review 52 (3) : 527 à 550.
Kindleberger, C.P. 1969. American Business Abroad: Six Lectures on Direct Investment. New Haven, Connecticut : Yale University Press. 225 p.
Lim, K., 2017. Firm-to-firm Trade in Sticky Production Networks. 2017 Annual Meeting of the Society for Economic Dynamics. Edinburgh, Écosse. 22 au 24 juin 2017. Disponible au lien suivant : https://economicdynamics.org/meetpapers/2017/paper_280.pdf (consulté le 2 mai 2018).
Nocke, V., et S. Yeaple. 2007. « Cross-border mergers and acquisitions vs. greenfield foreign direct investment: The role of firm heterogeneity ». Journal of International Economics 72 (2) : 336 à 365.
Ramondo, N., V. Rappoport et K.J. Ruhl. 2016. « Intra firm trade and vertical fragmentation in U.S. multinational corporations ». Journal of International Economics 98 (2) : 51 à 59.
Rauch, J., 1999. « Networks versus markets in international trade ». Journal of International Economics 48 (1) : 7 à 35.
Rauch, J.E. 2001. « Business and Social Networks in International Trade ». Journal of Economic Literature 39 (4) : 1177 à 1203.
Williamson, O.E. 1979. « Transaction-Cost Economics: The Governance of Contractual Relations. » The Journal of Law & Economics 22 (2) : 233 à 261.
Williamson, O.E. 2008. « Outsourcing: Transaction cost economics and supply chain management ». Journal of Supply Chain Management 44 (2) : 5 à 16.
Yeaple, S.R., 2013. « The Multinational Firm ». Annual Review of Economics 5 (1) : 193 à 217.
- Date de modification :