Direction des études analytiques : documents de recherche
Parcourir tout le trajet : estimer l’effet des frontières provinciales sur le commerce lorsque l’unité géographique compte
 Consulter la version la plus récente.
Consulter la version la plus récente.
Information archivée dans le Web
L’information dont il est indiqué qu’elle est archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Elle n’est pas assujettie aux normes Web du gouvernement du Canada et elle n’a pas été modifiée ou mise à jour depuis son archivage. Pour obtenir cette information dans un autre format, veuillez communiquer avec nous.
par Robby K. Bemrose, W. Mark Brown et Jesse Tweedle
Division de l’analyse économique
Statistique Canada
Remerciements
Les auteurs tiennent à remercier Danny Leung, Bart Los, Dennis Novy, Trevor Tombe, Dan Trefler, Yoto Yotov et les participants à la série de séminaires de la Division de l’analyse économique et de l’Université du Québec à Montréal et aux réunions du North American Regional Science Council et de la Western Regional Science Association pour leurs commentaires utiles. Les auteurs sont reconnaissants de l’aide à la recherche offerte par Javad Sadeghzadeh, Olena Melin et Afshan Dar-Brodeur.
Résumé
Pour de nombreux biens, comme les produits laitiers et les boissons alcoolisées, la présence d’obstacles (non tarifaires) importants pour le commerce provincial est largement reconnue. Si ces obstacles non tarifaires importent, le commerce intraprovincial devrait ainsi être plus vigoureux que le commerce interprovincial, toutes choses égales par ailleurs. Toutefois, il est difficile de comparer les niveaux d’échanges intraprovinciaux et interprovinciaux entre eux, puisque le commerce intraprovincial penche fortement en faveur des flux sur de courtes distances. Lorsque les flux ne sont pas correctement pris en compte par les modèles gravitationnels des échanges commerciaux, les niveaux des échanges intraprovinciaux (les effets des frontières provinciales) ont tendance à être surestimés. Pour résoudre ce problème, de nouveaux flux des échanges infraprovinciaux, élaborés à partir d’un ensemble de fichiers de transport au niveau de la transaction, sont utilisés pour estimer les effets des frontières provinciales. La sensibilité des résultats à la distance est observée en estimant des modèles sur des unités géographiques normalisées de taille variable (provinces, régions économiques, divisions de recensement) ainsi que sur des unités géographiques non normalisées (grilles hexagonales), de taille variable et différemment positionnées, et ce, en effectuant une série de simulations. Les résultats montrent que les effets des frontières provinciales diminuent à mesure que la distance est mesurée avec plus d’exactitude et que les unités géographiques sont plus précises et uniformes sur le plan de la forme et de la taille. Néanmoins, les effets de frontière se maintiennent, l’équivalent tarifaire ad valorem implicite s’établissant à 6,9 %. Cette constatation contraste avec ce qui est observé aux États-Unis, où les effets des frontières entre les États sont éliminés lorsque des approches similaires sont appliquées.
Mots clés : Effets de frontière, commerce interprovincial, coûts de transport, modèle gravitationnel
Journal of Economic Literature : R4 R15 F15
Sommaire
Pour de nombreux biens, comme les produits laitiers et les boissons alcoolisées, la présence d’obstacles (non tarifaires) importants pour le commerce provincial est largement reconnue. Si ces obstacles non tarifaires importent, le commerce intraprovincial devrait ainsi être plus vigoureux que le commerce interprovincial, toutes choses égales par ailleurs. Toutefois, il est difficile de comparer les niveaux d’échanges intraprovinciaux et interprovinciaux entre eux, puisque le commerce intraprovincial penche fortement en faveur des flux sur de courtes distances. Lorsque les flux ne sont pas correctement pris en compte, les niveaux des échanges intraprovinciaux (les effets des frontières provinciales) ont tendance à être surestimés.
Pour résoudre ce problème, des flux des échanges infraprovinciaux, élaborés à partir d’un ensemble de fichiers de transport au niveau de la transaction, sont utilisés pour estimer les effets des frontières provinciales pour la période allant de 2004 à 2012. Chaque livraison est mesurée en fonction de la valeur, du coût, de la distance d’expédition, du point d’origine et du point de destination. Selon les points d’origine et de destination (latitude et longitude), les flux entre des régions de toutes tailles peuvent être utilisés, ce qui permet d’estimer les flux entre les régions à l’intérieur et à l’extérieur des frontières provinciales.
L’analyse montre que le commerce intraprovincial est toujours plus vigoureux que ne l’est le commerce interprovincial lorsqu’on considère la distance entre les régions commerciales ainsi que la capacité des unités d’échange à générer et à absorber les flux commerciaux. La vigueur relative du commerce intraprovincial dépend des unités géographiques utilisées pour mesurer le commerce. Lorsque les unités géographiques utilisées sont les provinces, les échanges au sein de la province sont estimés être 2,26 fois plus grands que les échanges interprovinciaux. Cette observation laisse entendre que les obstacles au commerce interprovincial sont équivalents à l’imposition d’un droit de douane ad valorem de 13,6 %. Lorsque les régions infraprovinciales sont utilisées plutôt que les provinces, l’équivalent tarifaire lié à l’effet de frontière diminue pour se situer à 6,9 %. Cette estimation plus faible s’est avérée robuste après avoir fait l’objet d’un grand nombre de tests statistiques, ce qui contraste également avec ce qui est observé aux États-Unis, où les effets des frontières entre les États sont éliminés lorsque des approches similaires sont appliquées.
1. Introduction
Pour certains biens, comme les produits laitiers et les boissons alcoolisées, on observe la présence d’obstacles (non tarifaires) importants au commerce interprovincial. Toutefois, la mesure dans laquelle ces obstacles ont une incidence sur le niveau des échanges interprovinciaux n’est pas claire. L’une des façons d’évaluer cet élément est de déterminer si les provinces font davantage d’échanges au sein d’elles-mêmes qu’entre elles. Si les obstacles non tarifaires sont importants, leur empreinte devrait ainsi être visible dans le profil des échanges provinciaux.
Les efforts visant à étudier si c’est le cas ont été entravés par un manque de données permettant d’estimer le flux des échanges à l’intérieur des provinces, puisque le commerce entre les provinces est comparé à ces flux intérieurs. Le problème est résolu en élaborant des estimations des échanges intraprovinciaux et interprovinciaux à partir d’un ensemble de flux au niveau de la transaction. Au moyen d’un modèle gravitationnel des échanges, la présente étude compare les échanges entre les régions à l’intérieur des provinces aux échanges entre les provinces, fournissant ainsi une estimation de la mesure dans laquelle les économies provinciales sont intégrées en raison du commerce. Autrement dit, il s’agit d’une estimation de la mesure dans laquelle les frontières provinciales freinent le commerce provincial, ce qui est communément appelé « l’effet de frontière ».
En s’appuyant sur les premiers travaux menés par McCallum (1995), une abondante documentation a été consacrée à la mesure de l’effet de frontière, à l’échelle nationale et infranationale. Au fil du temps, les effets de frontière estimés ont diminué, puisque les premières spécifications de McCallum ont été modifiées pour tenir compte des effets de l’accès au marché et de la concurrence (Anderson et van Wincoop, 2003; Anderson et Yotov, 2010), les estimations de la distance ont été affinées (Head et Mayer, 2010) et de nouveaux estimateurs ont été appliqués (Head et Mayer, 2014). Pourtant, la documentation a régulièrement indiqué que le commerce est plus vigoureux à l’intérieur des pays qu’entre eux.
Bien qu’une grande partie de la documentation portait sur la mesure de l’effet de frontière entre les pays, les mêmes méthodes ont été appliquées aux régions infranationales. La documentation portant sur les effets des frontières infranationales pointe également vers une réduction des effets lorsque des méthodes plus précises sont appliquées. Dans certains cas, cela a conduit à l’élimination complète de l’effet de frontière. Aux États-Unis, les estimations initialement élevées des effets des frontières entre les États (Wolf, 2000) ont été réduites en appliquant des mesures plus précises de la distance (Hillberry et Hummels, 2003; Head et Mayer, 2010; Crafts et Klein, 2015), en restreignant le flux des échanges aux expéditions provenant des fabricants uniquement (Hillberry et Hummels, 2003), en utilisant une spécification en panel et en contrôlant la migration interne (Millimet et Osang, 2007). On a aussi utilisé des unités géographiques plus précises pour définir les unités d’échanges infranationales (Hillberry et Hummels, 2008; voir aussi Coughlin et Novy, 2016).
Deux stratégies peuvent être utilisées pour élaborer une estimation des effets des frontières provinciales. La première stratégie consiste à affiner les estimateurs types actuels afin d’atténuer les erreurs de mesure et les biais dus aux variables omises. Il s’agit de l’approche utilisée par Agnosteva, Anderson et Yotov (2014), qui profitent de la nature par panel des mesures actuelles du commerce intraprovincial et interprovincial pour estimer les effets des frontières provinciales. La deuxième stratégie, et sans doute une stratégie complémentaire, utilisée dans la présente étude vise à améliorer les données sur le commerce intraprovincial et interprovincial afin de répondre aux préoccupations soulevées dans la documentation tout en utilisant une stratégie d’estimation pour réduire les biais restants.
Une attention particulière est accordée à l’influence de la distance mesurée (Head et Mayer, 2010) et à l’unité géographique (Hillberry et Hummels, 2003 et 2008). Head et Mayer (2010) montrent que les mesures inexactes de la distance peuvent biaiser les estimations de l’effet de frontière vers le haut, puisque les distances intrarégionales ont tendance à être surestimées par rapport aux distances interrégionales. En estimant la distance en fonction des flux de point à point des marchandises, ce biais est effectivement éliminé. Hillberry et Hummels (2008) démontrent que, lorsque la taille de l’unité géographique de l’analyse est réduite, les obstacles estimés aux échanges entre les États sont réduits à zéro. Les obstacles entre les États sont un biais dû à l’échelle géographique utilisée pour obtenir des estimations. Cet effet s’explique par le plus grand nombre de flux sur de courtes distances pour des biens intermédiaires qui sont traités dans la Commodity Flow Survey (CFS) des États-Unis, ce qui se traduit par des estimations inexactes quant à la distance parcourue par les biens. Une entrave au présent travail, en particulier dans le contexte canadien, est le manque de données infraprovinciales détaillées qui tiendrait compte de l’effet de biais des flux sur de courtes distances. Le problème est résolu en tirant profit des microdonnées utilisées pour calculer les flux commerciaux intraprovinciaux et interprovinciaux.
L’analyse montre que le commerce intraprovincial est toujours plus vigoureux que le commerce interprovincial lorsqu’on considère la distance entre les régions commerciales ainsi que la capacité des unités d’échange à générer et à absorber les flux commerciaux. La vigueur relative du commerce intraprovincial dépend des unités géographiques utilisées pour la mesurer et, dans une moindre mesure, de la mesure de distance utilisée. Lorsqu’on utilise les régions infraprovinciales plutôt que les provinces, l’équivalent tarifaire de l’effet de frontière passe de 13,6 % à 6,9 %. Cet équivalent tarifaire correspond à l’estimation qui se maintient après l’application d’un vaste ensemble de vérifications visant à atténuer les effets de biais vers le haut découlant de l’erreur de spécification du modèle (effets non linéaires de la distance) et de l’unité géographique (taille et emplacement de l’unité géographique). Il s’agit, par conséquent, d’une estimation faible et prudente qui contraste fortement avec les estimations enregistrées aux États‑Unis, où l’application d’approches similaires élimine les effets des frontières entre les États.
Le reste de l’article est organisé de la façon suivante. La section 2 (Élaboration des données) examine la méthode utilisée pour estimer les échanges entre les unités géographiques infraprovinciales et dresse un portrait du commerce canadien intérieur. Une attention particulière est accordée à la façon dont ces estimations sont étalonnées en fonction des totaux des échanges intraprovinciaux et interprovinciaux connus et à la validité sous-jacente de ces estimations. La section 3 (Modèle et stratégie d’estimation) décrit la structure du modèle d’échanges et la détermination d’un estimateur approprié. La section 4 (Estimations du modèle) présente des estimations intraprovinciales et interprovinciales normalisées et des estimations des échanges en fonction des unités géographiques infraprovinciales ainsi qu’un ensemble de vérifications de la robustesse testant les biais liés à l’erreur de spécification et au problème d’unité spatiale modifiable (Modifiable Areal Unit Problem — MAUP). La section 5 (Équivalent tarifaire de l’effet de frontière) estime les équivalents tarifaires des obstacles au commerce interprovincial sous forme agrégée et par marchandise. La section 6 (Conclusion) présente un sommaire des résultats et de leurs effets.
2. Élaboration des données
Jusqu’à présent, l’analyse du commerce intérieur du Canada s’est limitée à l’échelle provinciale, en se fondant sur les tableaux du commerce des comptes provinciaux d’entrées-sorties ou sur la structure des échanges provinciaux déclarés dans l’Enquête annuelle des manufactures (voir Brown [2003] pour obtenir des renseignements sur cette structure). Le présent document élabore un nouvel ensemble de données de point à point flexible au niveau de la transaction qui permet de mesurer le flux des échanges entre un ensemble presque illimité d’unités géographiques infraprovinciales, fournissant ainsi un moyen d’aborder un bon nombre des enjeux économétriques soulevés dans la documentation. Puisque cette base de données est nouvelle, il est utile de décrire la façon dont elle a été créée ainsi que certaines de ses caractéristiques de base.
2.1 Création de la base de données
Les données proviennent du fichier des transports terrestres (FTT) de Statistique Canada qui fournit des estimations de la valeur des biens échangés entre les régions au Canada et entre le Canada et les États-Unis. Le FTT est tiré de l’Enquête sur l’origine et la destination des marchandises transportées par camion (ODMTC) et de bordereaux d’expédition par chemin de fer pour la période allant de 2002 à 2012, l’analyse se concentrant sur la période allant de 2004 à 2012Note 1. Puisque ces données sont élaborées à partir de données provenant de lettres de transport d’entreprises de camionnage et de bordereaux d’expédition par chemin de fer, le FTT, dans sa forme originale, constitue un « fichier logistiqueNote 2 ».
Le FTT mesure la circulation des marchandises à partir du point où elles sont ramassées jusqu’au point où elles sont déposées. Ces points ne représentent pas nécessairement les endroits où les marchandises sont fabriquées ou sont utilisées. Toutefois, l’analyse exige que la base de données puisse saisir le niveau des échanges entre les régions infraprovinciales, ce qui est intégré comme concept dans le modèle gravitationnel des échanges appliqué dans le cas présent. L’objectif de l’analyse présente beaucoup de points communs avec les objectifs prévus lors de l’élaboration des comptes provinciaux d’entrées-sorties :
« Lorsqu’on analyse l’interdépendance économique, il est nécessaire de maintenir le lien entre les sources d’approvisionnement initiales et les consommateurs finaux, par bien ou service. Par conséquent, le point d’origine (c.-à-d. la source d’approvisionnement initiale) est celui où les biens et services sont produits ou celui où les biens sont vendus à même les stocks des producteurs, des grossistes et des détaillants. Le point de destination (c.-à-d. le consommateur final) est le point où les biens et services sont achetés à titre d’articles de consommation courante, d’éléments de la formation de capital, d’intrants dans le processus de production d’autres biens et services, ou d’ajouts aux stocks. » (Généreux et Langen, 2002, p. 7.)
Afin de convertir le FTT, en passant d’un fichier logistique à un fichier portant sur les échanges, les flux des échanges provinciaux provenant des comptes d’entrées-sorties sont utilisés pour étalonner les flux intraprovinciaux et interprovinciaux par marchandise. Un poids est accordé à chaque transaction dans le FTT, ce qui fait en sorte que l’agrégat s’ajoute au total pour le flux intraprovincial ou interprovincial correspondant provenant des tableaux d’entrées-sorties. La procédure d’établissement de données repères et, en particulier, l’établissement d’une concordance entre les codes de la Classification des produits par entrées-sorties (CPES) et les codes de la Classification type des biens transportés (CTBT) (Statistique Canada, s.d.a) dans le FTT, sont présentés à l’annexe A.3. Un résumé de la procédure est présenté ici.
La valeur nominale des échanges entre les régions infraprovinciales (ci-après régions) et , , est la somme de la valeur du poids de sondage de la livraison indexé par entre la région d’origine et la région de destination Note 3, multipliée par le poids de référence pour la livraison :
Le poids de référence pour la livraison correspond au poids de l’enquête pour la livraison, , multiplié par le poids de référence de la paire de provinces pour la marchandise expédiée; la notation pour la paire de provinces et le produit est supprimée afin de simplifier l’exposé. Le poids de référence est déterminé de sorte que les échanges entre une paire de provinces donnée (ou à l’intérieur d’une même province) s’ajoutent aux totaux connus pour les comptes commerciaux provinciaux par marchandise et par année.
La figure 1 illustre la procédure d’établissement de données repères. Prenons un exemple simple de flux de véhicules fabriqués à divers endroits en Ontario et finalement utilisés à divers endroits au Manitoba et en Saskatchewan. Les véhicules peuvent d’abord être livrés à un centre de distribution au Manitoba, et une partie de la livraison envoyée en Saskatchewan, ce qui est représenté par les flux non pondérés dans le quadrant supérieur gauche de la figure. D’un point de vue logistique, il s’agit d’une représentation correcte des flux, mais d’un point de vue commercial, le flux de l’Ontario, où les véhicules sont fabriqués, jusqu’en Saskatchewan, où ils sont utilisés, est sous-estimé, et le flux du Manitoba jusqu’à la Saskatchewan est quant à lui surestimé. Comme l’illustre la figure 1 (quadrant supérieur droit), l’établissement de données repères d’après les tableaux d’entrées-sorties fait augmenter les flux de l’Ontario à la Saskatchewan et réduit (à zéro) ceux allant du Manitoba à la Saskatchewan.
La stratégie de pondération repose sur l’existence d’un flux dans le FTT entre chaque paire de provinces. Autrement, il n’y a rien à pondérer à la hausse (ou à la baisse) : . Le résultat est l’absence de flux entre les paires de provinces (moitié inférieure de la figure 1). Si ces « liens brisés » sont trop fréquemment observés ou corrélés avec la distance entre les paires de provinces, l’établissement de données repères se traduit par des estimations biaisées. Une source de biais est simplement remplacée par une autre.

Description de la figure 1
Le titre de la figure 1 est « Transformation des flux logistiques en flux commerciaux, ensembles de liens complets et brisés ».
Le diagramme illustre le processus d’établissement des points de référence, représenté par quatre triangles délimités par des flèches de différentes largeurs. Les triangles ne sont pas tous complètement délimités, puisque les flèches représentent les flux des échanges. Sur les trois pointes de chacun des quatre triangles se trouvent de petits triangles désignés Ontario, Manitoba et Saskatchewan. L’Ontario est la province d’origine des flux commerciaux.
Deux de ces quatre triangles représentent l’ensemble de liens complets, un pour les véhicules non étalonnés et l’autre pour les véhicules étalonnés.
Dans le triangle pour les véhicules non étalonnés, les biens sont expédiés entre l’Ontario, le Manitoba et la Saskatchewan.
Dans le triangle pour les véhicules étalonnés, les biens sont expédiés seulement entre l’Ontario et le Manitoba et entre l’Ontario et la Saskatchewan.
Les deux autres triangles représentent l’ensemble de liens brisés, un pour les véhicules non étalonnés et l’autre pour les véhicules étalonnés.
Dans le triangle pour les véhicules non étalonnés, les biens sont expédiés seulement entre l’Ontario et le Manitoba et entre le Manitoba et la Saskatchewan.
Dans le triangle pour les véhicules étalonnés, les biens sont expédiés seulement entre l’Ontario et le Manitoba. La source de la figure 1 est « Statistique Canada ».
Le tableau 1 présente le rapport des flux interprovinciaux et intraprovinciaux du FTT pondérés en fonction des flux actuels provenant des tableaux d’entrées-sorties. Puisque les provinces de l’Atlantique présentaient un plus grand nombre de liens brisés, en particulier avec l’Ouest canadien, les données ont été agrégées pour l’établissement de données repères. En conséquence, relativement peu de paires de provinces affichent une importante perte d’échanges. Le pourcentage global correspond à 99 % des niveaux commerciaux en ce qui a trait aux entrées-sorties. Les flux intraprovinciaux ont tendance à enregistrer une moins grande perte, mais cette tendance est faible. Autrement, il ne semble pas y avoir de pertes importantes liées à la distance. Par exemple, la perte observée pour les exportations des régions de l’Atlantique vers l’Alberta ou la Colombie-Britannique est sensiblement la même que celle observée pour l’Ontario. L’effet de ces liens brisés est testé de façon plus poussée ci-dessous en estimant le modèle gravitationnel au moyen des flux provinciaux dérivés des entrées-sorties et des flux pondérés; les deux ensembles de données fournissent des résultats similaires sur le plan qualitatif (voir la section 4).
| Destination | ||||||||
|---|---|---|---|---|---|---|---|---|
| Provinces de l’Atlantique | Qc | Ont. | Man. | Sask. | Alb. | C.-B. | Total | |
| pourcentage | ||||||||
| Origine | ||||||||
| Provinces de l’Atlantique | 99 | 99 | 89 | 94 | 77 | 94 | 89 | 95 |
| Québec | 99 | 99 | 100 | 98 | 94 | 98 | 98 | 99 |
| Ontario | 100 | 100 | 100 | 99 | 98 | 100 | 100 | 100 |
| Manitoba | 93 | 97 | 95 | 96 | 95 | 97 | 95 | 96 |
| Saskatchewan | 87 | 96 | 96 | 95 | 98 | 97 | 97 | 97 |
| Alberta | 89 | 97 | 98 | 97 | 99 | 100 | 100 | 99 |
| Colombie-Britannique | 96 | 82 | 99 | 97 | 96 | 99 | 98 | 97 |
| Total | 98 | 99 | 99 | 97 | 98 | 99 | 98 | 99 |
| Note : Les proportions sont établies en fonction des niveaux moyens des échanges entre 2004 et 2012. Source : Statistique Canada, calculs des auteurs. |
||||||||
Bien que l’établissement de données repères tienne compte des niveaux d’échanges intraprovinciaux et interprovinciaux, la structure des échanges, particulièrement à l’intérieur des provinces, peut quant à elle être touchée par le fonctionnement du système de transport ou de distribution. Autrement dit, la prévalence des flux sur de plus courtes distances, dictés par la logistique, peut être plus grande. Cela entraîne des répercussions importantes puisque, lorsqu’ils sont mis en commun avec les flux interprovinciaux, ces flux intraprovinciaux sur de plus courtes distances tendent à être sous-estimés, ce qui a pour effet de biaiser vers le haut les effets des frontières interprovinciales estimés.
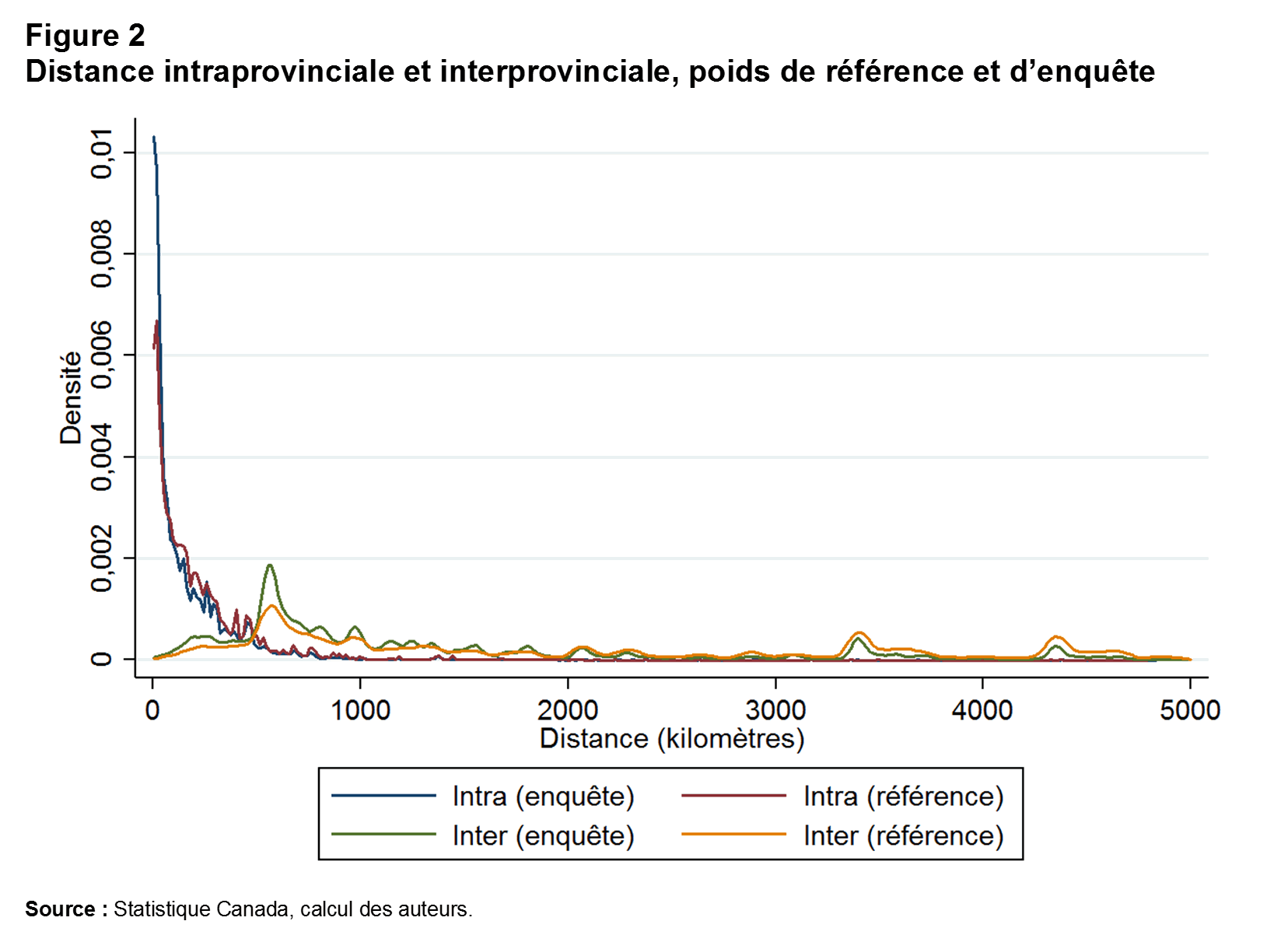
Comme dans le petit exemple simple précédent, l’établissement de données repères devrait faire en sorte d’étendre davantage le commerce interprovincial, puisque les flux sur de courtes distances (vers, ou depuis, les centres de distribution ou les grossistes) sont pondérés vers le bas et que les flux sur de plus longues distances, à partir du point où les biens sont produits jusqu’au point où ils sont utilisés, sont pondérés vers le haut. Le phénomène est clairement illustré à la figure 2 qui présente les noyaux de densité des distances de livraisons, les poids d’enquête et la pondération des points de référence et des poids d’enquête ensemble ainsi que les distances de livraisons divisées entre les flux interprovinciaux et intraprovinciaux. Comme prévu, pour les livraisons interprovinciales, l’établissement des données repères tend à réduire l’importance des flux sur de plus courtes distances (moins de 1 000 km) et à accroître l’importance des flux sur de plus longues distances, particulièrement ceux excédant 3 000 km. Pour le commerce intraprovincial, après l’établissement des données repères, les flux sur de courtes distances sont réduits, puisque les marchandises importées (par exemple, les chaussures et les vêtements) qui sont distribuées localement sont pondérées à la baisse. Pourtant, à l’intérieur des provinces, la prévalence des flux sur de courtes distances, dictés par la logistique, peut être plus grande. Cet effet peut être testé en déterminant si la distance a un effet plus marqué sur le commerce intraprovincial que sur le commerce interprovincial. Les résultats indiquent que ce n’est pas le cas (l’annexe B.1 aborde ce sujet en détail).
Description de la figure 2
Le titre de la figure 2 est « Distance intraprovinciale et interprovinciale, poids de référence et d’enquête ».
Il s’agit d’un graphique linéaire des noyaux de densité.
L’axe horizontal est « Distance (kilomètres) ». Il commence à 0 et se termine à 5 000, avec une ligne guide tous les 1 000 points.
L’axe vertical est « Densité ». Il commence à 0 et se termine à 0,01, avec une ligne guide pour chaque 0,002 point.
Il y a 4 séries dans cette figure.
Le titre de la série 1 est « Intra (enquête) », soit la densité de la distance intraprovinciale pondérée par les poids d’enquête. Elle est vraiment haute au départ, puis elle diminue significativement après environ 100 kilomètres, pour ensuite rester plane.
Le titre de la série 2 est « Intra (référence) », soit la densité de la distance intraprovinciale pondérée par les poids de référence. Elle est vraiment haute au départ, puis elle diminue significativement après environ 100 kilomètres, pour ensuite rester plane. Elle n’est pas aussi haute que pour la série 1 au départ, mais elle la croise à 50 kilomètres environ et elle demeure plus élevée que la série 1 par la suite.
Le titre de la série 3 est « Inter (enquête) », soit la densité de la distance interprovinciale pondérée par les poids d’enquête. Elle est basse au départ, puis elle connaît un pic à environ 500 kilomètres et demeure relativement constante par la suite, avec une pointe à environ 3 400 kilomètres et 4 400 kilomètres. Elle est plus haute que pour les séries 1 et 2.
Le titre de la série 4 est « Inter (référence) », soit la densité de la distance interprovinciale pondérée par les poids de référence. Elle est basse au départ, puis elle connaît un pic à environ 50 kilomètres et demeure relativement constante par la suite, avec une pointe à environ 3 400 kilomètres et 4 400 kilomètres. Elle est plus haute que pour les séries 1 et 2. Elle est légèrement plus basse que la série 3 avant 2 000 kilomètres, puis légèrement plus haute par la suite.
La source de la figure 2 est « Statistique Canada, calcul des auteurs ».
Pour de plus amples renseignements, veuillez communiquer avec Statistique Canada à STATCAN.infostats-infostats.STATCAN@canada.ca.
2.2 Structure des échanges
Avant d’estimer les obstacles au commerce interprovincial, il est utile de dresser un portrait des échanges entre les provinces et entre les régions infraprovinciales.
Le tableau 2 montre la structure des exportations entre les provinces (et le Canada atlantique), présentant une moyenne pour la période allant de 2004 à 2012. À l’exception de la Saskatchewan, du Manitoba et du Canada atlantique, la majorité des échanges se produit à l’intérieur des provinces. Cela n’est pas nécessairement dû aux obstacles interprovinciaux, mais possiblement à l’incidence de la distance sur les flux commerciaux (figure 2). Le tableau 2 illustre également la tendance des provinces à échanger avec les provinces voisines. Le marché d’exportation le plus important du Canada atlantique est le Québec; celui de la Saskatchewan est l’Alberta. Cependant, bien que les flux intraprovinciaux soient importants, la structure des échanges à l’intérieur des provinces n’est pas connue.
| Provinces de l’Atlantique | Qc | Ont. | Man. | Sask. | Alb. | C.-B. | Total | |
|---|---|---|---|---|---|---|---|---|
| pourcentage | ||||||||
| Provinces de l’Atlantique | 28 | 34 | 24 | 5 | 1 | 5 | 4 | 100 |
| Québec | 1 | 67 | 22 | 1 | 1 | 4 | 3 | 100 |
| Ontario | 1 | 11 | 76 | 2 | 1 | 6 | 4 | 100 |
| Manitoba | 1 | 7 | 18 | 48 | 6 | 14 | 6 | 100 |
| Saskatchewan | 0 | 4 | 13 | 8 | 44 | 24 | 6 | 100 |
| Alberta | 0 | 4 | 9 | 4 | 5 | 68 | 10 | 100 |
| Colombie-Britannique | 0 | 5 | 8 | 2 | 2 | 15 | 68 | 100 |
| Total | 1 | 23 | 42 | 4 | 4 | 16 | 10 | 100 |
| Note : Les parts sont établies en fonction des niveaux moyens des échanges entre les régions pour la période allant de 2004 à 2012. La somme des pourcentages peut ne pas être égale à 100 % en raison de l’arrondissement. Source : Statistique Canada, calculs des auteurs. |
||||||||
La structure des échanges intraprovinciaux et interprovinciaux est déterminée par un ensemble discret de points d’origine et de destination. La carte 1 affiche les emplacements qui sont desservis par camion ou par transport ferroviaire. Chaque point représente un emplacement participant aux échanges, générant une zone potentielle où des biens seront très probablement fabriqués et utilisés. Sur cette zone, une unité géographique donnée (province, région économique (RE), division de recensement (DR) ou autre configuration) est superposée afin de générer un ensemble de flux agrégés.
Comme le montre la carte 1, bien que la plupart des échanges se produisent à l’intérieur des provinces, il semble que le plus fort potentiel d’échanges se situe dans des zones encore plus concentrées géographiquement. Cette observation se confirme lorsqu’on calcule la valeur du commerce total (exportations plus importations) dans l’ensemble des RE en pourcentage de l’ensemble du commerce de biens au Canada. Une petite minorité de RE représente une part disproportionnée du commerce intérieur. Parmi les 73 RE, trois d’entre elles (Toronto, Montréal et péninsule de HamiltonNiagara) représentent 30 % de la valeur des biens expédiés au Canada. La RE de Toronto a enregistré un plus grand nombre d’échanges intérieurs et extérieurs que toute autre province, à l’exception de l’Ontario et du Québec. Ainsi, la compréhension du commerce provincial passe par la compréhension des échanges entre les régions infraprovinciales, en particulier dans les grands centres urbains.

Description de la carte 1
Le titre de la carte 1 est « Densité des points d’origine et de destination ».
La carte présente le Canada et montre les limites provinciales et territoriales.
Elle indique la densité des emplacements dans le Fichier des transports terrestres (FTT).
Les endroits affichant une grande quantité d’activité commerciale au Canada sont marqués en rouge.
Les endroits présentant la plus grande activité commerciale sont concentrés autour des grandes villes : Toronto, Ottawa, Montréal, Québec, Calgary, Edmonton et Vancouver.
Les autres endroits enregistrent une quantité moyenne d’activités commerciales.
Il y a moins d’activité dans les zones rurales.
Les notes pour la carte 1 sont les suivantes :
Notes : Chaque point représente un hexagone de 4 km de côté (42 km2) comportant une ou plusieurs origines/destinations (code postal ou terminus de chemin de fer). La gradation de couleur du jaune à l’orange au rouge dénote un plus grand nombre d’origines/destinations.
La source de la carte 1 est « Statistique Canada, calcul des auteurs ».
Pour de plus amples renseignements, veuillez communiquer avec Statistique Canada à STATCAN.infostats-infostats.STATCAN@canada.ca.
3. Modèle et stratégie d’estimation
L’estimation des effets des frontières provinciales repose sur l’élaboration de données de qualité suffisante pour générer des estimations bien fondées ainsi que sur un modèle et un estimateur appropriés pour les données.
3.1 Modèle d’échanges
En règle générale, dans les articles publiés (Head et Mayer, 2014)Note 4, les échanges commerciaux entre les régions et sont traités comme une fonction multiplicative de la capacité de de desservir les marchés d’exportation , comme la capacité d’absorption du marché d’exportation dans et comme une mesure qui rend compte de l’effet des coûts du commerce entre et :
où est un terme constant. On peut exprimer cette forme générale comme un modèle gravitationnel structurel :
où est la valeur de la production dans et est la somme des exportations entre tous les partenaires commerciaux (y compris lui-même) , et est la valeur de consommation dans et est la somme des importations entre tous les partenaires commerciaux (y compris lui-même) . Les termes et sont des termes de résistance multilatérale (Anderson et van Wincoop, 2003), où
est une mesure de l’accès au marché pour la région exportatrice , et mesure le niveau de la concurrence dans le marché . Les coûts commerciaux sont pris en compte en fonction de la distance entre et et d’un ensemble de variables binaires qui tiennent compte des échanges intraprovinciaux et intrarégionaux .
3.2 Estimateur
On peut estimer l’équation (3) en substituant des effets fixes pour et , en ajoutant un terme d’erreurs multiplicatif et en établissant l’exposant du côté droit :
où et prennent en compte la production de et le potentiel de marché de et la taille de et le niveau de concurrence de , respectivement.
Cette stratégie d’estimation est devenue la méthode normalisée pour estimer le modèle gravitationnelNote 5 (Anderson et Yotov, 2012), et ce, en raison de la facilité d’estimation et parce que les effets fixes peuvent récupérer des données inobservables propres aux points d’origine et de destination qui peuvent biaiser les estimations basées sur des données complètes (Anderson, 2010; Head et Mayer, 2014).
Le biais attribuable à une variable manquante est particulièrement important dans le présent travail. Bien que tous les efforts soient faits pour assigner les flux des échanges là où les biens sont effectivement fabriqués et utilisés, il peut y avoir des cas où un point de destination agit comme centre de distribution, gonflant ainsi son niveau d’exportations et d’importations. En outre, certaines provinces (par exemple, la Colombie-Britannique) peuvent avoir des liens plus étroits avec les marchés internationaux que d’autres provinces, ce qui réduit leur rôle en tant que partenaire commercial national. Dans les deux cas, les effets fixes devraient tenir compte de ces variables inobservables qui influent sur le niveau des échanges à l’intérieur d’une région et à l’extérieur de celle-ci (Head et Mayer, 2014).
La méthode des moindres carrés ordinaires (MCO), soit l’approche normalisée pour estimer l’équation (5), introduit deux sources potentielles de biais. Tout d’abord, les estimations obtenues par les MCO pour un modèle log-linéaire multiplicatif sont biaisées en présence d’erreurs hétéroscédastiques (Santos Silva et Tenreyro, 2006). Ensuite, les estimations obtenues par les MCO sont biaisées dans les cas comportant un plus grand nombre de flux nuls, lesquels sont écartés lorsque le modèle gravitationnel est estimé au moyen de la méthode des MCO (Head et Mayer, 2014). Cette dernière source de biais est particulièrement importante dans le cas présent, puisque les modèles sont estimés en utilisant les flux entre les régions infraprovinciales, ce qui se traduit par un grand nombre de flux nuls entre les paires de régions commerciales.
La première étape pour résoudre ces problèmes est de déterminer si le terme d’erreurs est hétéroscédastique. Pour ce faire, le test Manning et Mullahy (2001) est appliqué. Il est estimé en fonction des spécifications suivantes :
où est le niveau logarithmique prévu des échanges d’après les estimations obtenues par les MCO à l’équation (5) et est la différence entre les données et les valeurs prédites à partir du même estimateur. Sans flux nuls, Head et Mayer (2014) obtiennent lorsque le processus de génération de données produit des erreurs normales logarithmiques, mais lorsque le processus produit des erreurs hétéroscédastiques (Poisson). Au tableau 3, les estimations de sont présentées pour les estimations par province, par RE et par DR. Pour les échanges provinciaux, l’estimation ponctuelle pour est de 2,11, ce qui sous-entend des erreurs normales logarithmiques. Toutefois, lorsque le modèle est estimé par RE et par DR, les estimations ponctuelles pour sont d’environ 1,7. Pour les RE, où la proportion de flux nuls est d’environ 8 %, l’estimation se rapproche de l’estimation attendue d’après les simulations de Monte Carlo (figure 4, dans Head et Mayer, 2014). En ce qui concerne les estimations pour les DR, où près de la moitié des paires affichent des flux nuls, la valeur attendue de est de 1,6, et l’estimation réelle est de 1,7. Cette estimation se rapproche de celle relevée par Head et Mayer lorsqu’ils obtiennent des estimations de à partir de données réelles. En conséquence, dans les deux cas, l’estimation pour est significativement différente de 2, ce qui donne à penser que l’estimateur par les MCO est inapproprié.
| Unité géographique | κ | Intervalle de confiance à 95 % |
Nombre d’observations |
|
|---|---|---|---|---|
| Borne inférieure | Borne supérieure | |||
| Province | 2,11 | 1,92 | 2,30 | 100 |
| Région économique | 1,71 | 1,68 | 1,74 | 5 069 |
| Division de recensement | 1,68 | 1,67 | 1,69 | 47 156 |
| Notes : κ estimé à partir de l’équation (6) en utilisant les flux des échanges entre les provinces, les régions économiques et les divisions de recensement. Lorsque κ est significativement différent de 2, le test peut être interprété comme indiquant que les moindres carrés ordinaires ne sont pas l’estimateur approprié. Source : Statistique Canada, calculs des auteurs. |
||||
La seconde étape consiste à évaluer l’estimateur approprié en présence de flux nuls et d’erreurs hétéroscédastiques. D’après les résultats de la simulation de Monte Carlo, Head et Mayer (2014) constatent que l’estimateur du pseudo maximum de vraisemblance de Poisson (PMV-Poisson) tend à produire le moins de biais. Il s’agit ainsi de l’estimateur privilégié, en particulier lorsque les estimations sont basées sur des flux entre les régions infraprovinciales. Il est également privilégié puisqu’il reproduit parfaitement les estimations du modèle d’équations structurelles (Fally, 2015) d’Anderson et van Wincoop (2003).
3.3 Géographie et estimation
L’analyse repose sur l’agrégation des données ponctuelles en un ensemble d’unités géographiques. Les unités établies en fonction de la Classification géographique type (appelées ci-après unités géographiques normalisées, par exemple, les RE et les DR) ne constituent que l’un d’un nombre presque illimité d’unités géographiques possibles. Comme l’ont démontré Hillberry et Hummels (2008), les estimations des obstacles au commerce peuvent être fortement influencées par l’unité géographique choisie.
Les conclusions d’Hillberry et Hummels (2008) constituent un exemple de problème d’unité spatiale modifiable (MAUP) [traduction] : « [...] la sensibilité des résultats d’analyse à la définition des unités pour lesquelles des données réelles sont recueillies » (Fotheringham et Wong, 1991, p. 1025). Le MAUP est caractérisé à la fois par un effet d’échelle et de zonage. Autrement dit, les résultats analytiques dépendent de la résolution spatiale (effet d’échelle) et de la morphologie (effet de zonage) de l’unité géographique utilisée pour agréger les données (Páez et Scott, 2005).
Ces problèmes se posent pour les statistiques multivariées, y compris les modèles d’interaction spatiale comme le modèle gravitationnel (Fotheringham et Wong, 1991; Amrhein et Flowerdew, 1992; Briant, Combes et Lafourcade, 2010). En particulier, Briant, Combes et Lafourcade (2010) montrent que les résultats des modèles gravitationnels sont plus sensibles aux effets d’échelle et moins sensibles aux effets de zonage. Toutefois, ces problèmes sont jugés secondaires par rapport aux problèmes de spécification du modèle (par exemple, le biais dû aux variables omises). Néanmoins, comme le démontre Amrhein (1995), un MAUP peut survenir même lorsque les problèmes de spécification sont pris en compte.
Ainsi, les effets d’agrégation géographique doivent être pris en compte. Pour ce faire, il faut appliquer différentes unités géographiques aux données. Deux stratégies sont alors utilisées. La première consiste à déterminer la sensibilité des résultats lors de l’application des unités géographiques normalisées, à savoir définir les régions d’échanges en fonction des provinces, des RE et des DR. La deuxième stratégie tire profit de l’interprétation d’Arbia (1989) qui montre que les biais résultant des effets d’échelle et de zonage de l’unité géographique peuvent être minimisés en s’assurant que les unités géographiques sont identiques et spatialement indépendantes. Une grille hexagonaleNote 6 est superposée aux points d’origine et de destination géocodés, créant ainsi une unité géographique identique et spatialement indépendante (carte 2). Les hexagones qui traversent les frontières provinciales sont séparés et traités comme des unités géographiques discrètes.
Toutefois, même si l’utilisation d’unités géographiques hexagonales contribue possiblement à minimiser le biais créé par l’agrégation des données, elle ne l’élimine pas complètement. Les problèmes soulevés par l’effet d’échelle et de zonage subsistent. Puisqu’il n’existe aucune échelle théoriquement prédéterminée pour les hexagones, la sensibilité des résultats quant à la taille doit être testée. La couverture géographique des hexagones de 75 km et de 225 km de côté illustrée aux cartes A-1 et B-1 (à la carte 2) présente un exemple de cette constatation. Les plus petits hexasgones couvrent des parties de régions métropolitaines, tandis que les plus grands hexagones peuvent en englober plusieurs. De même, bien que la forme des hexagones ne change pas, le zonage demeure important puisque les hexagones sont positionnés de façon arbitraire sur les points d’origine et de destination. À la carte A-1, Toronto est répartie sur deux hexagones, tandis qu’à la carte A-2, elle est répartie sur trois. Les effets d’échelle et de zonage sont testés en exécutant le modèle pour différentes échelles et différents zonages.

Description de la carte 2
Le titre de la carte 2 est « Taille et positionnement des grilles hexagonales ».
La carte contient quatre cartes : carte A-1, carte A-2, carte B-1, carte B-2. Chaque carte représente la même zone. Ces quatre cartes représentent la densité des emplacements dans le Fichier des transports terrestres (FTT), ainsi que les grilles hexagonales qui composent les unités géographiques dans le présent document.
Les notes pour la carte 2 sont les suivantes :
Notes : Les cartes A-1 et A-2 présentent deux différentes superpositions des hexagones de 75 km de côté sur le sud de l’Ontario et le Québec, où chaque point représente un point d’origine et de destination. Les cartes B-1 et B-2 présentent la même chose, mais avec les hexagones de 225 km de côté. Les hexagones doivent respecter les limites provinciales et sont répartis entre les provinces.
La source de la carte 2 est « Statistique Canada, calcul des auteurs ».
Pour de plus amples renseignements, veuillez communiquer avec Statistique Canada à STATCAN.infostats-infostats.STATCAN@canada.ca.
4. Estimations du modèle
Dans cette section, les effets de frontière sont estimés en utilisant des estimations du flux des échanges à l’échelle de la province, ce qui fournit un scénario de base. Les effets de frontière sont ensuite estimés au moyen d’unités géographiques infraprovinciales. Cela constitue la base de l’analyse. Le reste de la discussion porte sur un ensemble de vérifications de la robustesse, en accordant une attention particulière à la sensibilité des estimations aux MAUP, aux autres spécifications du modèle ou à une combinaison de ces éléments.
4.1 Estimations types selon la province
Les obstacles interprovinciaux au commerce sont mesurés en comparant les niveaux agrégés des échanges intraprovinciaux et interprovinciaux. Cette comparaison poursuit plusieurs objectifs. Premièrement, en comparant le niveau réel des échanges interprovinciaux aux estimations de référence, la sensibilité des résultats à la perte d’échanges due à l’établissement de données repères peut être déterminée. Deuxièmement, les estimations obtenues par les MCO, par le PMV-Poisson et par le PMV-Gamma peuvent être comparées sans flux nuls. En fonction de leurs conditions de premier ordre, l’estimateur Poisson met davantage l’accent sur l’écart absolu entre les flux réels et prévus, tandis que les estimations obtenues par les MCO et le PMV-Gamma mettent l’accent sur l’écart en pourcentage et, ainsi, devraient donner des résultats similaires (Head et Mayer, 2014). Troisièmement, les résultats provinciaux servent de points référence pour comparer les obstacles estimés au commerce interprovincial en analysant les échanges entre les régions infraprovinciales.
Le tableau 4-1 montre les effets estimés de la distance et de la province sur le commerce provincial, au moyen des flux basés sur les entrées-sorties et ceux dérivés après l’établissement de données repères. Le modèle est estimé en utilisant une version de l’équation (5), modifiée de façon appropriée, et en utilisant le niveau moyen des échanges provinciaux de 2004 à 2012 comme variable dépendante. Plusieurs observations peuvent être dégagées de ce tableau.
Premièrement, les estimations reposant sur les flux d’entrées-sorties et les flux pondérés sont similaires. Les estimations pour la province même ont tendance à être moindres lorsque les estimations de référence sont utilisées, mais l’effet est relativement faible, particulièrement lorsque l’estimateur Poisson est utilisé. Puisqu’il y a relativement peu de perte de généralité résultant de l’établissement de données repères, le reste de la discussion porte sur ces estimations.
Deuxièmement, il existe des effets de frontière, peu importe l’estimateur utilisé. L’estimateur par les MCO, lequel n’est pas significatif pour les flux pondérés, fait exception. Lorsqu’on utilise les estimations de référence des entrées-sorties, les effets de frontière varient de 1,61 (MCO) à 2,26 (Poisson). Autrement dit, les échanges à l’intérieur de la province sont de 61 % à 126 % plus élevés que les échanges interprovinciaux lorsque la distance et la résistance multilatérale sont prises en compte.
L’avantage d’établir les estimations des échanges à partir des données de livraison est qu’il est possible d’obtenir une mesure plus précise de la distance parcourue par les biens à l’intérieur des provinces et entre elles. La sensibilité des résultats à la mesure de la distance peut être testée en comparant les estimations fondées sur la distance du réseau à celles fondées sur la distance orthodromique, laquelle est habituellement utilisée dans la documentation (annexe A.4).
| Distance du réseau | ||||||
|---|---|---|---|---|---|---|
| Entrées-sorties | Référence | |||||
| MCO | Poisson | Gamma | MCO | Poisson | Gamma | |
| Distance | ||||||
| Coefficient | -1,025Note ** | -0,661Note ** | -0,999Note ** | -1,077Note ** | -0,686Note ** | -1,0780Note ** |
| Erreur-type | 0,0458 | 0,0496 | 0,0453 | 0,0576 | 0,0522 | 0,0537 |
| Dans la province | ||||||
| Coefficient | 0,607Note ** | 0,865Note ** | 0,775Note ** | 0,479 | 0,816Note ** | 0,634Note * |
| Erreur-type | 0,2230 | 0,0807 | 0,1900 | 0,2890 | 0,0827 | 0,2540 |
| Constante | ||||||
| Coefficient | 12,31Note ** | 9,916Note ** | 12,42Note ** | 11,70Note ** | 9,515Note ** | 12,08Note ** |
| Erreur-type | 0,4100 | 0,5590 | 0,3730 | 0,6300 | 0,8770 | 0,5350 |
| Effet de frontière | 1,83 | 2,38 | 2,17 | 1,61 | 2,26 | 1,89 |
| Valeur R au carré | 0,954 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,959 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Nombre d’observations | 100 | 100 | 100 | 100 | 100 | 100 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||
| Distance orthodromique | ||||||
|---|---|---|---|---|---|---|
| Entrées-sorties | Référence | |||||
| MCO | Poisson | Gamma | MCO | Poisson | Gamma | |
| Distance | ||||||
| Coefficient | -1,058Note ** | -0,778Note ** | -1,037Note ** | -1,100Note ** | -0,806Note ** | -1,106Note ** |
| Erreur-type | 0,0462 | 0,0571 | 0,0436 | 0,0613 | 0,0591 | 0,0564 |
| Dans la province | ||||||
| Coefficient | 0,747Note ** | 0,780Note ** | 0,840Note ** | 0,653Note * | 0,728Note ** | 0,743Note ** |
| Erreur-type | 0,1940 | 0,0907 | 0,1710 | 0,2740 | 0,0882 | 0,2490 |
| Constante | ||||||
| Coefficient | 12,01Note ** | 10,49Note ** | 12,17Note ** | 11,29Note ** | 10,12Note ** | 11,70Note ** |
| Erreur-type | 0,4050 | 0,5470 | 0,3600 | 0,6440 | 0,8480 | 0,5350 |
| Effet de frontière | 2,11 | 2,18 | 2,32 | 1,92 | 2,07 | 2,10 |
| Valeur R au carré | 0,956 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,959 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Nombre d’observations | 100 | 100 | 100 | 100 | 100 | 100 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||
La façon dont la distance est mesurée a de l’importance. En moyenne, la distance du réseau est 33 % plus grande que la distance orthodromique. En raison de la compression de la distance, le paramètre de distance devrait être davantage négatif pour les estimations fondées sur la distance orthodromique, ce qui est vrai, quel que soit l’estimateur (voir le tableau 4-2). Par ailleurs, les distances orthodromiques à l’intérieur des provinces sont, en termes relatifs, surestimées (annexe A.4), ce qui biaise à la hausse l’effet à l’intérieur de la province. L’estimateur par les MCO et l’estimateur Gamma montrent cet effet, contrairement à l’estimateur Poisson, dont le coefficient de distance semble plutôt mettre le biais en évidence.
4.2 Estimations selon les unités géographiques infraprovinciales
Les estimations des effets des frontières provinciales fondées sur la comparaison des flux du commerce intraprovincial et interprovincial peuvent demeurer biaisées si ces unités ne captent pas efficacement la structure des échanges. Comme le montrent Hillberry et Hummels (2008), si les flux sur de courtes distances prédominent et ne sont pas correctement captés par la mesure de la distance interne, l’effet de frontière estimé peut être biaisé à la hausse.
Pour mieux établir la présence et la vigueur des effets des frontières provinciales, les flux commerciaux intraprovinciaux et interprovinciaux sont mesurés au moyen d’unités géographiques infraprovinciales de différentes tailles et morphologies. Puisque les échanges peuvent être observés à la fois à l’intérieur des unités géographiques infraprovinciales et entre de telles unités, une variable binaire est incluse pour le commerce à l’intérieur de l’unité (dans la région). Cette variable devrait prendre en compte les non-linéarités dans l’effet de la distance pour les flux sur de plus courtes distances ou les différences dans la nature des échanges dans la région ou entre les régions. Les échanges dans la région sont plus susceptibles de comprendre des flux sur de courtes distances entre les fabricants et les centres de distribution, entre les centres de distribution et les magasins (Hillberry et Hummels, 2003) et entre les fournisseurs en amont et les utilisateurs en aval pour les entrées intermédiaires (Hillberry et Hummels, 2008).
En se concentrant sur les unités infraprovinciales, on introduit le problème de flux nuls entre les unités d’échanges. L’ensemble des unités d’échanges est défini comme étant les unités utilisant ou fabricant les biens. Les unités qui ne prennent pas part au commerce des biens, soit au sein d’elles-mêmes ou avec les autres unités, sont exclues. Cela peut découler du fait que l’on n’observe aucune production mesurable de biens dans l’unité ou découler d’une variabilité d’échantillonnage. Puisque les estimations sont fondées sur la valeur moyenne des échanges sur neuf ans, l’ampleur de l’effet de la variabilité d’échantillonnage risque d’être faible. Bien sûr, les unités incluses dans l’ensemble d’unités d’échanges n’entretiennent pas de relations commerciales avec toutes les unités potentielles, ce qui entraîne des flux nuls. Les flux nuls peuvent être dus au hasard (encore une fois, la variabilité d’échantillonnage), ou ils peuvent être de nature structurelle (les producteurs engagent des coûts supérieurs au seuil de démarcation). Pour permettre la présence de flux nuls, l’estimateur Poisson est utilisé. Pour les flux nuls, la distance entre les régions est mesurée en distance orthodromiqueNote 7.
Sur les quatre unités géographiques utilisées dans le cadre de l’analyse, deux (les RE et les DR) s’appuient sur les unités géographiques normalisées; les deux autres sont des grilles hexagonales de 75 km et de 225 km de côté. Si les hexagones faisaient plus de 225 km de côté, certaines des plus petites provinces en comporteraient très peu. Par ailleurs, des hexagones de moins de 75 km de côté entraîneraient un si grand nombre d’effets fixes devant être estimés que l’estimateur PMV-Poisson ne pourrait converger de manière fiable. Le tableau 5 présente les caractéristiques des unités.
| Norme | Hexagones | |||
|---|---|---|---|---|
| Régions économiques |
Divisions de recensement |
225 km de côté | 75 km de côté | |
| Unités géographiques | nombre | |||
| Total | 76 | 288 | 90 | 511 |
| Ensemble des unités d’échanges | 73 | 282 | 90 | 380 |
| Superficie | kilomètres carrés | |||
| Moyenne | 74 930 | 19 397 | 131 528 | 14 614 |
| Écart-type | 129 347 | 59 759 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Minimum | 247 | 193 | 131 528 | 14 614 |
| 25e centile | 10 416 | 1 863 | 131 528 | 14 614 |
| Médiane | 20 880 | 3 771 | 131 528 | 14 614 |
| 75e centile | 77 903 | 15 202 | 131 528 | 14 614 |
| Maximum | 747 158 | 747 158 | 131 528 | 14 614 |
| ... n'ayant pas lieu de figurer Notes : L’ensemble des unités d’échanges est défini comme les unités géographiques participant à des échanges commerciaux mesurés, excluant celles dans les territoires. La superficie des unités géographiques infraprovinciales est calculée pour l’ensemble des unités d’échanges. Source : Statistique Canada, calculs des auteurs. |
||||
En optant pour les RE comme unité d’échanges, le paramètre de distance tend à être moins négatif que pour les estimations fondées sur la province, et la région est susceptible de prendre en compte l’effet non linéaire des flux sur de courtes distances (tableau 6). L’estimation pour la province est plus faible, se traduisant en un effet de frontière de 2,10. En utilisant les DR, c’est-à-dire une unité élémentaire fondamentale des RE, le nombre de paires d’échanges potentielles passe de 5 329 à 79 524. Pour cet ensemble beaucoup plus grand de plus petites unités d’échanges, l’effet de frontière diminue pour s’établir à 1,97.
Tant pour les petits que pour les grands hexagones, les effets dans la région ne sont pas statistiquement significatifs et les effets dans la province demeurent quant à eux significatifs, mais nettement inférieurs à ceux observés pour les unités géographiques normalisées. Le résultat est un effet de frontière qui tombe dans une fourchette restreinte allant de 1,60 (grands hexagones) à 1,62 (petits hexagones). En d’autres mots, on estime que le commerce intraprovincial est de 60 % à 62 % plus vigoureux que le commerce interprovincial, toutes choses égales par ailleurs (tableau 6).
| Unité géographique | |||||
|---|---|---|---|---|---|
| Type | Hexagone | Région de tri d’acheminement | |||
| Région économique |
Division de recensement |
225 km de côté |
75 km de côté |
||
| Distance | |||||
| Coefficient | -0,551Note ** | -0,573Note ** | -0,820Note ** | -0,742Note ** | -0,426Note ** |
| Erreur-type | 0,0461 | 0,0278 | 0,0620 | 0,0357 | 0,0146 |
| Dans la région | |||||
| Coefficient | 0,408Note ** | 0,467Note ** | -0,101 | -0,0215 | 1,052Note ** |
| Erreur-type | 0,1380 | 0,1210 | 0,1270 | 0,1170 | 0,0966 |
| Dans la province | |||||
| Coefficient | 0,743Note ** | 0,679Note ** | 0,472Note ** | 0,483Note ** | 0,909Note ** |
| Erreur-type | 0,0951 | 0,0633 | 0,0872 | 0,0783 | 0,0421 |
| Constante | |||||
| Coefficient | 6,981Note *** | 7,094Note *** | 3,142Note *** | 2,540Note *** | 2,015Note *** |
| Erreur-type | 0,4900 | 0,3590 | 0,7760 | 0,4770 | 0,3830 |
| Effet de frontière | 2,10 | 1,97 | 1,60 | 1,62 | 2,48 |
| Nombre d’observations | 5 329 | 77 274 | 8 619 | 132 862 | 2 574 640 |
Source : Statistique Canada, calculs des auteurs. |
|||||
Ces résultats contrastent avec ceux de Hillberry et Hummels (2008), qui constatent que l’effet des frontières entre les États est un biais dû à l’unité géographique utilisée pour mesurer le commerce intérieur. Toutefois, dans leur analyse, les effets de frontière disparaissaient seulement lorsqu’on avait recours à une unité géographique encore plus précise que celle utilisée dans la présente étude, à savoir les codes ZIP américains à cinq chiffres. Pour tenir compte de cette observation, le modèle a été exécuté de nouveau en utilisant les régions de tri d’acheminement (RTA), soit le plus proche équivalent canadien des codes postaux américainsNote 8. Les estimations ponctuelles pour la province demeuraient positives et significatives (tableau 6), mais à un niveau plus élevé que pour les autres unités géographiques. Même avec une unité géographique très précise, les effets des frontières provinciales se maintiennent : une observation robuste et s’appliquant à un large ensemble de spécifications (partie 4.3.4).
Les estimations des effets des frontières provinciales et infraprovinciales indiquent que l’unité géographique choisie a de l’importance, mais les données permettant de tirer des conclusions solides demeurent insuffisantes. Deux questions doivent être réglées. La première est la mesure dans laquelle les résultats sont sensibles aux MAUP, notamment les effets d’échelle et de zonage (taille et emplacement des hexagones). Il est difficile de savoir si les variations dans les effets des frontières provinciales parmi les hexagones de différentes tailles (ou en l’absence de ceux-ci) sont compensées par la variabilité résultant du positionnement des hexagones. La deuxième question est de savoir si un effet non linéaire de la distance sur les échanges a une incidence sur les estimations des effets des frontières provinciales. L’élasticité de la distance varie selon les unités géographiques et les estimateurs et, comme Head et Mayer (2014) l’indiquent, une variation du terme de la distance entre les estimateurs Poisson et Gamma peut être le signe d’une erreur de spécification du modèle, ce que présente le tableau 4. Ainsi, il est nécessaire d’évaluer plus rigoureusement la façon dont l’unité géographique et la spécification du modèle, particulièrement les effets non linéaires de la distance, ont une incidence sur les effets de frontière estimés.
4.3 Robustesse des estimations infraprovinciales
La robustesse des estimations est testée en quatre étapes. La première teste la sensibilité des résultats aux MAUP. La deuxième vérifie si un effet non linéaire de la distance sur les échanges peut avoir une incidence sur les estimations des effets des frontières provinciales. La troisième combine les deux premières étapes en déterminant jusqu’à quel point les résultats sont sensibles lorsque le MAUP et l’effet non linéaire de la distance sont pris en compte. La quatrième étape renvoie à l’analyse de Hillberry et Hummel (2008) afin de déterminer si les effets des frontières provinciales se maintiennent lorsque les RTA sont utilisées comme unités d’échanges après l’application de leur spécification et de leur estimateur ainsi que du modèle entièrement spécifié.
4.3.1 Problème d’unité spatiale modifiable
Pour vérifier la sensibilité des résultats au MAUP, les modèles sont exécutés de nouveau sur des grilles hexagonales de différentes tailles et décalées de façon aléatoire. Pour une taille donnée d’hexagone, la grille est superposée à la masse terrestre du Canada, et chaque point d’origine et de destination est codé de manière à correspondre à sa province et à son hexagone respectif. Le centroïde de chaque hexagone est ensuite déplacé vers un point aléatoire à l’intérieur d’un cercle circonscrit par ses frontières. L’ensemble des points est limité au cercle circonscrit, puisque le fait de les glisser sur plus d’une unité ne fait que reproduire le motif. Les points d’origine et de destination sont recodés pour représenter leur province et leur hexagone. La grille est décalée de façon aléatoire 100 foisNote 9, générant un ensemble de paramètres qui décrit la sensibilité des estimations par rapport à l’emplacement de la grille (MAUP, effet de zonage) pour une taille donnée d’hexagone. Cet exercice est répété pour sept tailles d’hexagones différentes, augmentant par tranche de 25 km de côté, pour passer de 75 km à 225 km. Cela permet de constater la mesure dans laquelle les résultats sont sensibles à la taille des hexagones (effet d’échelle et MAUP).
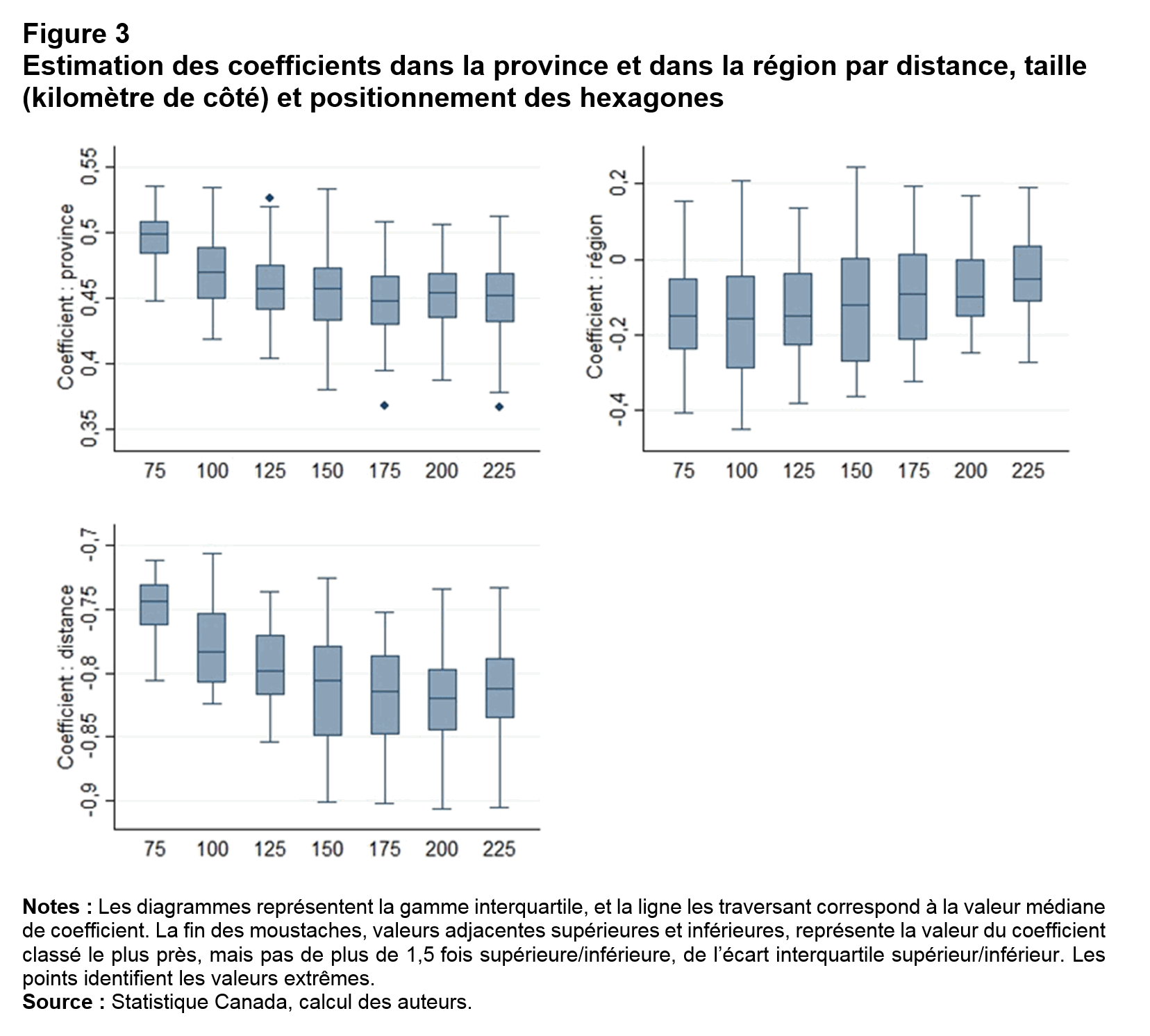
Pour représenter la répartition des coefficients découlant des simulations pour les principales variables province, région (hexagone) et distance la figure 3 présente des diagrammes de quartiles selon la taille des hexagones. Les boîtes représentent l’écart interquartile, et la ligne les traversant correspond à la valeur médiane du coefficient. Le point terminal des moustaches (valeurs adjacentes supérieures et inférieures) représente la valeur du coefficient classé le plus près de l’écart interquartile supérieur (inférieur), sans être supérieur (inférieur) à 1,5 fois l’écart. Les points désignent les valeurs extrêmes.
Description de la figure 3
Le titre de la figure 3 est : « Estimation des coefficients dans la province et dans la région par distance, taille (kilomètre de côté) et positionnement des hexagones ».
Cette figure comporte trois diagrammes de quartiles pour l’estimation des coefficients de régression.
L’axe horizontal de chaque diagramme compte sept catégories : 75, 100, 125, 150, 175, 200 et 225.
L’axe vertical du premier diagramme est « Coefficient : dans la province ». Il commence à 0,35 et se termine à 0,55, avec des lignes guide pour chaque 0,05.
La valeur médiane du premier diagramme pour la catégorie 75 est 0,5. La valeur médiane pour la catégorie 225 est 0,45. Les autres valeurs médianes se trouvant entre ces deux valeurs.
L’axe vertical du deuxième diagramme est « Coefficient : dans la région ». Il commence à -0,4 et se termine à 0,2, avec des lignes guide pour chaque 0,2.
La valeur médiane du deuxième diagramme pour la catégorie 75 est environ -0,15. La valeur médiane pour la catégorie 225 est environ -0,05. Les autres valeurs médianes se trouvant entre ces deux valeurs. Le tracé supérieur de chaque catégorie dans le deuxième diagramme est supérieur à 0.
L’axe vertical du troisième diagramme est « Coefficient : distance ». Il commence à -0,9 et se termine à -0,7, avec des lignes guide pour chaque 0,05.
La valeur médiane du troisième diagramme pour la catégorie 75 est environ -0,75. La valeur médiane pour la catégorie 225 est environ -0,82. Les autres valeurs médianes se trouvant entre ces deux valeurs.
Les notes pour la figure 3 sont les suivantes :
Notes : Les diagrammes représentent la gamme interquartile, et la ligne les traversant correspond à la valeur médiane de coefficient. La fin des moustaches, valeurs adjacentes supérieures et inférieures, représente la valeur du coefficient classé le plus près, mais pas de plus de 1,5 fois supérieure/inférieure, de l’écart interquartile supérieur/inférieur. Les points identifient les valeurs extrêmes.
La source de la figure 3 est « Statistique Canada, calcul des auteurs ».
Pour de plus amples renseignements, veuillez communiquer avec Statistique Canada à STATCAN.infostats-infostats.STATCAN@canada.ca.
En ce qui a trait aux résultats pour la province, les valeurs médianes des coefficients varient de 0,50 pour les plus petits hexagones à 0,45 pour les plus grands (effet d’échelle), et les coefficients convergent asymptotiquement vers la valeur médiane inférieure au fur et à mesure que la taille des hexagones augmente. Ces résultats concordent avec les observations de Coughlin et Novy (2016) qui affirment que si les échanges au sein de petites unités sont particulièrement vigoureux, au fur et à mesure que la taille de l’unité augmente, les effets de frontière tendent à diminuer. L’emplacement de la grille hexagonale (effet de zonage) a un effet plus considérable sur les estimations, puisque la différence entre les valeurs adjacentes inférieures et supérieures du diagramme est plus grande que celle entre les médianes des hexagones de différentes tailles. Cette observation contraste avec celle de Briant, Combes et Lafourcade (2010), qui constatent que l’effet d’échelle est plus considérable que celui de zonage. De façon plus générale, le fait de passer à une unité géographique uniforme entraîne un effet qualitatif sur l’effet de frontière estimé et ce résultat se maintient lorsqu’on tient compte de l’effet de la taille et de l’emplacement des hexagones sur les estimations.
4.3.2 Effets non linéaires de la distance
Les variations dans les résultats entre les hexagones de différentes tailles peuvent provenir d’un effet non linéaire de la distance sur les échanges, dont l’une des manifestations est l’effet négatif de la taille de l’hexagone sur le coefficient de la distance (figure 3). Au fur et à mesure que les hexagones deviennent plus petits, la distance de livraison moyenne diminue. Si ces flux sur de courtes distances plus répandus sont sous-estimés, l’effet des frontières provinciales, lui, sera surestimé, puisque les échanges intraprovinciaux se produisent sur de plus courtes distances que les échanges interprovinciaux (figure 2). Cela semble être le cas, puisqu’il existe une association positive entre les coefficients de la province et ceux de la distance (figure 3).
Pour au moins deux raisons, on s’attend à ce que l’effet de la distance sur les échanges varie. Premièrement, les prix facturés par les entreprises de camionnage, par exemple, comprennent des composantes de coûts fixes et variables (parcours de ligne). Puisque les coûts fixes par livraison sont d’environ 200 $ et que les coûts de parcours de ligne augmentent pour se situer à environ 0,80 $ par kilomètre (Brown, 2015), les prix incluant les coûts de transport seront effectivement uniformes sur de courtes distances. Deuxièmement, le regroupement endogène de fournisseurs en amont et d’entreprises en avalNote 10 ainsi que de réseaux de distribution en étoileNote 11 (Hillberry et Hummels, 2008) peut donner lieu à un large volume d’échanges sur de courtes distances et à une chute abrupte lorsque la distance de livraison va au-delà du « coin de la rue ». Les prix uniformes sur les courtes distances, combinés aux effets de regroupement ou de distribution, créent un ensemble complexe d’attentes. Pour ce qui est des flux sur de très courtes distances, l’effet de la distance sur les échanges peut être négatif (du moins après un court plateau), mais l’effet négatif de la distance sur les échanges au-delà de ces flux sur de très courtes distances devrait être initialement faible, puis se renforcer au fur et à mesure que les coûts variables surpassent l’effet des coûts fixes sur les tarifs de transport. Cette tendance qui se dégage des données fait en sorte qu’il faut aller au-delà de la forme quadratique type pour tenir compte des non-linéarités.
Pour tenir compte des effets non linéaires de la distance, le modèle est estimé de nouveau à l’aide d’une spline comportant des nœuds à 25 km, à 100 km et à 500 km (tableau 7) en utilisant les grilles hexagonales pour les estimations du tableau 6Note 12. D’après les résultats des hexagones plus petits, les élasticités de la distance concordent avec une forte baisse des livraisons sur de très courtes distances (reflétant le regroupement d’usines liées aux entrées-sorties, par exemple), tandis que l’effet non significatif de la distance pour les flux de 25 à 100 km concorde avec les tarifs de transports relativement constants qui sont facturés par les entreprises pour de courtes distances. Lorsque l’effet non linéaire de la distance est pris en compte, le coefficient pour la province est davantage similaire pour les diverses catégories de taille d’hexagone. Toutefois, en raison de la sensibilité des résultats quant à l’emplacement des grilles hexagonales, pour cet ensemble unique d’estimations ponctuelles, il est difficile de déterminer la similitude des estimations de l’effet de frontière entre les grands et les petits hexagones.
Finalement, une variable binaire est ajoutée pour les hexagones partageant une frontière (régions contiguës). On s’attend à ce que cette mesure de contiguïté tienne compte des flux sur de courtes distances traversant les frontières. Pour les grands et les petits hexagones, le coefficient de la région contiguë est non significatif, tandis que le coefficient pour la province diminue tout en restant significatif.
| Hexagone : 225 km de côté | Hexagone : 75 km de côté | |||
|---|---|---|---|---|
| Modèle 1 | Modèle 2 | Modèle 1 | Modèle 2 | |
| Distance | ||||
| 0 km à 25 km | ||||
| Coefficient | -1,356Note ** | -1,338Note ** | -0,932Note ** | -0,923Note ** |
| Erreur-type | 0,284 | 0,281 | 0,122 | 0,122 |
| 25 km à 100 km | ||||
| Coefficient | -0,544 | -0,561 | -0,268 | -0,276 |
| Erreur-type | 0,471 | 0,469 | 0,227 | 0,227 |
| 100 km à 500 km | ||||
| Coefficient | -0,836Note ** | -0,720Note ** | -0,711Note ** | -0,801Note ** |
| Erreur-type | 0,1190 | 0,1200 | 0,0598 | 0,0915 |
| Plus de 500 km | ||||
| Coefficient | -0,818Note ** | -0,772Note ** | -0,862Note ** | -0,858Note ** |
| Erreur-type | 0,0854 | 0,1090 | 0,0684 | 0,0689 |
| Dans la région | ||||
| Coefficient | -0,0608 | 0,2330 | 0,312Tableau 7 Note † | 0,1790 |
| Erreur-type | 0,173 | 0,237 | 0,161 | 0,199 |
| Dans la province | ||||
| Coefficient | 0,458Note ** | 0,412Note ** | 0,431Note ** | 0,418Note ** |
| Erreur-type | 0,0839 | 0,0755 | 0,0713 | 0,0709 |
| Régions contigües | ||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | 0,195 | Note ...: n'ayant pas lieu de figurer | -0,132 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | 0,1380 | Note ...: n'ayant pas lieu de figurer | 0,0972 |
| Constante | ||||
| Coefficient | 4,513Note ** | 4,184Note ** | 2,638Note ** | 2,746Note ** |
| Erreur-type | 0,807 | 0,833 | 0,494 | 0,501 |
| Effet de frontière | 1,58 | 1,51 | 1,54 | 1,52 |
| Nombre d’observations | 8 619 | 8 619 | 132 862 | 132 862 |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||
4.3.3 Effets non linéaires de la distance et problème d’unité spatiale modifiable
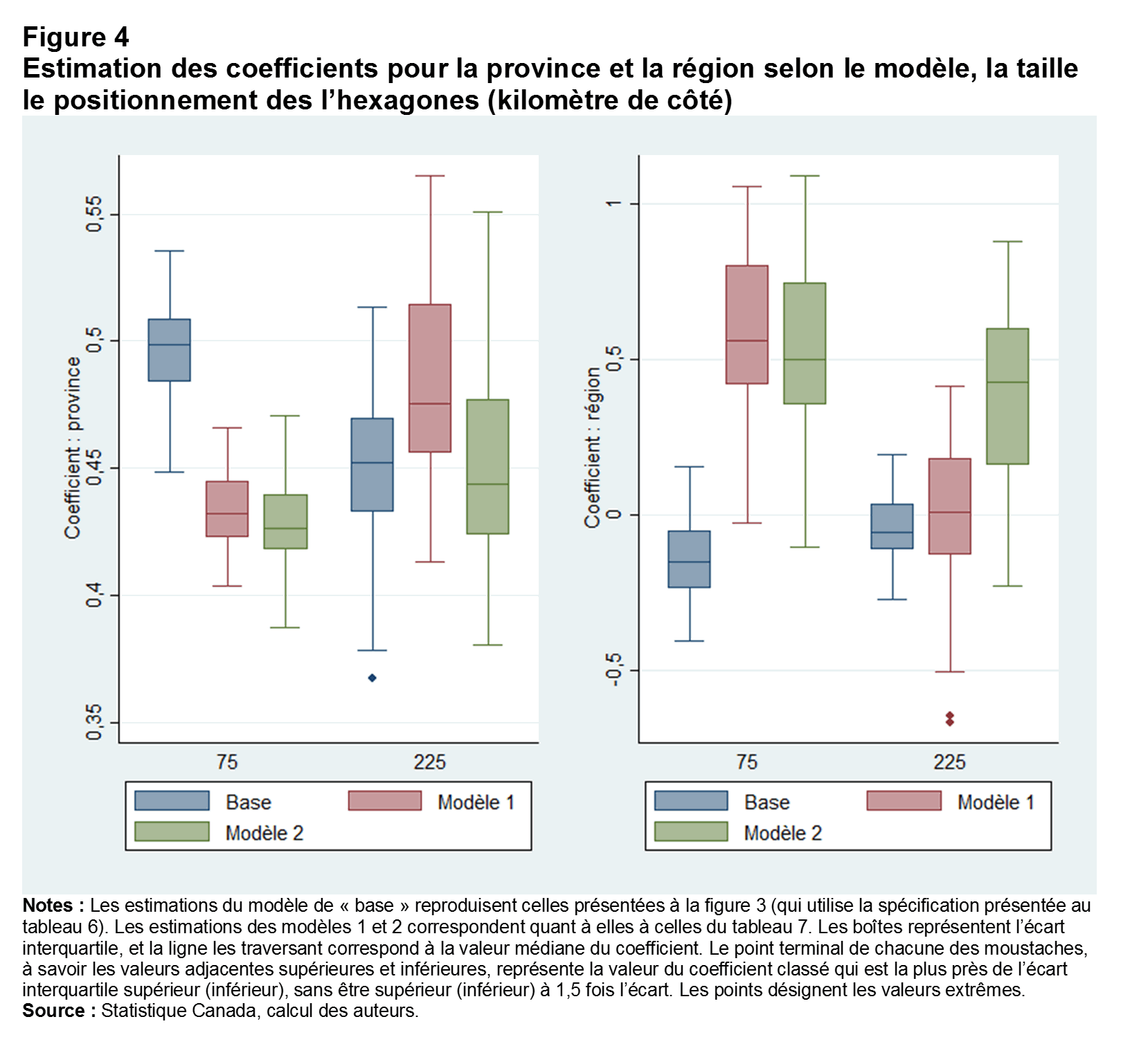
La vérification suivante vise à déterminer si le fait de tenir compte des effets non linéaires de la distance réduit le degré de variation des résultats entre les différentes tailles et les divers positionnements des hexagones. Encore une fois, cette vérification se fait par perturbation aléatoire des grilles hexagonales pour les plus grands hexagones (225 km de côté) et les plus petits (75 km de côté) et également pour les diverses spécifications du modèle. Les estimations du modèle de « base » reproduisent celles de la figure 3 (qui utilise la spécification du tableau 6). Les estimations des modèles 1 et 2 correspondent quant à elles à celles du tableau 7. Lorsque l’effet non linéaire de la distance est pris en compte, le coefficient médian des petits hexagones est réduit, mais celui des grands hexagones (figure 4) augmente, inversant ainsi la tendance illustrée à la figure 3. Lorsque la contiguïté est ajoutée au modèle (modèle 2), des effets des frontières provinciales statistiquement indiscernables pour les petits et les grands hexagones sont produits. Les coefficients des hexagones convergent également, mais seulement lorsque la contiguïté est prise en compte. Bien que les tendances centrales des distributions des coefficients des petits et des grands hexagones soient les mêmes, leurs variances ne le sont pas : les grands hexagones affichent un écart interquartile deux fois plus grand que celui des petits hexagones. Dans ce contexte, les effets de frontière des petits hexagones sont plus fiables.
Description de la figure 4
Le titre de la figure 4 est « Estimation des coefficients dans la province et dans la région par modèle, taille de l’hexagone (kilomètre de côté) et positionnement ».
Cette figure comporte deux diagrammes des quartiles pour l’estimation des coefficients de régression.
L’axe horizontal de chaque diagramme a deux catégories : 75 et 225.
Chaque catégorie dans chaque diagramme comporte trois séries : la série 1 est étiquetée « Base », la série 2 « Modèle 1 » et la série 3 est étiquetée « Modèle 2 ».
L’axe vertical du premier diagramme est « Coefficient : dans la province ».
Dans le premier diagramme, les valeurs médianes pour les trois séries à la catégorie 75 sont les suivantes : série 1, 0,5; série 2, environ 0,44; série 3, environ 0,43.
Dans le même diagramme, les valeurs médianes pour les trois séries à la catégorie 225 sont les suivantes : série 1, 0,45; série 2, environ 0,47; série 3, environ 0,45.
L’axe vertical du deuxième diagramme est « Coefficient : dans la région ».
Dans le deuxième diagramme, les valeurs médianes pour les trois séries à la catégorie 75 sont les suivantes : série 1, -0,1; série 2, environ 0,5; série 3, environ 0,5.
Dans le même diagramme, les valeurs médianes pour les trois séries à la catégorie 225 sont les suivantes : série 1, environ -0,1; série 2, environ 0,0; série 3, environ 0,45.
Les notes pour la figure 4 sont les suivantes :
Notes : Les estimations du modèle de « base » reproduisent celles présentées à la figure 3 (qui utilise la spécification présentée au tableau 6). Les estimations des modèles 1 et 2 correspondent quant à elles à celles du tableau 7. Les boîtes représentent la gamme interquartile, avec la ligne traversant la boîte représentant la valeur médiane de coefficient. La fin des moustaches, valeurs adjacentes supérieures et inférieures, représente la valeur du coefficient classé le plus près, mais pas de plus de 1,5 fois supérieure (inférieure), de l’écart interquartile supérieur (inférieur). Les points identifient les valeurs extrêmes.
La source de la figure 4 est « Statistique Canada, calcul des auteurs ».
Pour de plus amples renseignements, veuillez communiquer avec Statistique Canada à STATCAN.infostats-infostats.STATCAN@canada.ca.
4.3.4 Effets des frontières provinciales selon les régions de tri d’acheminement
Comme dernière vérification de la robustesse, l’analyse revisite Hillberry et Hummels (2008), ce qui permet de constater que les effets des frontières entre les États sont éliminés lorsque les échanges sont mesurés en utilisant les codes ZIP à cinq chiffres. Cela nécessite en premier lieu l’utilisation de l’estimateur (MCO) et la spécification du modèle (terme quadratique de la distance) provenant de leur analyse, puis l’application de l’estimateur privilégié (Poisson) et du modèle (effets de la distance estimés à l’aide d’une spline) utilisés précédemment.
Bien que le modèle et les estimateurs puissent être égalés, les résultats peuvent varier en raison des différences dans les données sous-jacentes. Premièrement, puisque les données du CFS utilisées par Hillberry et Hummels (2008) sont fondées sur les expéditeurs, il est possible que les livraisons soient limitées à celles des fabricants et qu’elles excluent celles des grossistes et des distributeurs. Toutefois, puisque les données utilisées sont fondées sur les transporteurs, il est impossible de faire la distinction entre les deux. Dans la mesure où les livraisons des grossistes sont plus localisées, il est plus probable que les échanges soient plus vigoureux sur de courtes distances, ce qui serait pris en compte par le terme pour la région (RTA).
Deuxièmement, puisque les estimations sont basées sur la moyenne des flux sur neuf années au sein des RTA, il est probable que les données comportent un plus grand nombre de flux par rapport aux données du CFS. En raison de cela et de la géographie du Canada, les données des RTA sont pondérées en fonction de flux sur de plus longues distances. La distance moyenne de livraison entre les RTA est de 1 679 km (1 049 miles), tandis que la distance moyenne de livraison entre les codes ZIP est de 837 km (523 miles) (Hillberry et Hummels, 2008). Puisque l’élasticité de la distance augmente (en termes absolus) en fonction de la distance de livraison, l’effet de la distance devrait être plus grand dans la présente analyse.
Le tableau 8 comprend les estimations, les trois premières colonnes illustrant le modèle équivalent à celui de Hillberry et Hummel (2008, tableau 2). La première colonne contient les estimations obtenues par les MCO; la deuxième et la troisième colonne comprennent les estimations obtenues par la méthode Poisson sans flux nuls et avec flux nuls, respectivement. Lorsque l’effet de la distance est évalué en utilisant une distance moyenne de 837 km, l’élasticité est de -0,42, soit plus du double de l’estimation de -0,19 basée sur les codes ZIP. Également, l’estimation ponctuelle pour la région (RTA) est beaucoup plus élevée. Ces disparités étaient attendues, en raison des différences dans les données sous-jacentes. Plus précisément, l’effet pour la province est positif et significatif lorsque l’estimateur, le modèle et l’unité géographique utilisés sont identiques à ceux d’Hillberry et Hummels.
L’application de l’estimateur Poisson réduit l’effet de la distance, puisque le plus grand nombre (généralement) de flux de courte distance a plus de poids. Lorsqu’il est évalué à une distance de 837 km, l’effet de la distance entraîne une élasticité de -0,25, et cette dernière est seulement légèrement inférieure en valeur absolue lorsqu’on ajoute les flux nuls. L’estimateur Poisson produit également de plus petits effets, mais qui sont toujours significatifs, pour la région et la province. L’inclusion de flux nuls se traduit par un coefficient positif de la distance jusqu’à 5 km, puis par une estimation ponctuelle à la baisse par la suite. Le fait d’ajouter les flux nuls augmente également les estimations ponctuelles pour la région et la province. L’effet fortement non linéaire de la distance que l’on observe lorsque l’estimateur Poisson est appliqué donne à penser que l’incidence de la distance sur les échanges doit être traitée de manière flexible. Cela est accompli en estimant une spline pour la distance.
| MCO | Poisson | |||||
|---|---|---|---|---|---|---|
| Modèle 1 | Modèle 1 | Modèle 2 | Modèle 3 | Modèle 4 | ||
| Distance | ||||||
| Coefficient | -0,490Note ** | -0,0105 | 0,217Note ** | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Erreur-type | 0,0220 | 0,0517 | 0,0566 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Distance au carré | ||||||
| Coefficient | 0,0104Note ** | -0,0353Note ** | -0,0661Note ** | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Erreur-type | 0,00178 | 0,00446 | 0,00479 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Distance | ||||||
| 0 km à 25 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | -0,0678 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,0587 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| 0 km à 10 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,303Note ** | Note ...: n'ayant pas lieu de figurer |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,110 | Note ...: n'ayant pas lieu de figurer |
| 0 km à 5 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,542Note * |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,245 |
| 5 km à 10 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,0223 |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,3470 |
| 10 km à 25 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | -0,461Note ** | -0,393Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,116 | 0,131 |
| 25 km à 100 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | -0,296Note ** | -0,198Note ** | -0,206Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,0668 | 0,0669 | 0,0667 |
| 100 km à 500 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | -0,497Note ** | -0,507Note ** | -0,505Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,0377 | 0,0374 | 0,0375 |
| Plus de 500 km | ||||||
| Coefficient | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | -0,767Note ** | -0,764Note ** | -0,764Note ** |
| Erreur-type | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,0235 | 0,0235 | 0,0235 |
| Dans la région | ||||||
| Coefficient | 2,357Note ** | 1,316Note ** | 1,494Note ** | 1,472Note ** | 1,561Note ** | 1,551Note ** |
| Erreur-type | 0,1040 | 0,1010 | 0,1010 | 0,1040 | 0,0998 | 0,1010 |
| Dans la province | ||||||
| Coefficient | 1,211Note ** | 0,468Note ** | 0,616Note ** | 0,592Note ** | 0,592Note ** | 0,593Note ** |
| Erreur-type | 0,0154 | 0,0361 | 0,0385 | 0,0393 | 0,0393 | 0,0393 |
| Constante | ||||||
| Coefficient | -3,117Note ** | 1,618Note ** | 1,123Note ** | 1,416Note ** | 0,793Tableau 8 Note † | 0,551 |
| Erreur-type | 0,217 | 0,399 | 0,408 | 0,415 | 0,442 | 0,472 |
| Nombre d’observations | 652 214 | 652 214 | 2 574 640 | 2 574 640 | 2 574 640 | 2 574 640 |
| Effet de frontière | 3,36 | 1,60 | 1,85 | 1,81 | 1,81 | 1,81 |
| Élasticité de la distance à 837 km | -0,42 | -0,25 | -0,23 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| Comprend les flux nuls | non | non | oui | oui | oui | oui |
... n'ayant pas lieu de figurer
Source : Statistique Canada, calculs des auteurs. |
||||||
Le modèle 2 utilise la même structure que le modèle 1 au tableau 7; il comporte des nœuds à 25 km, à 100 km et à 500 km. L’effet des frontières provinciales observé est plus faible que lorsque la forme quadratique est utilisée, mais il demeure significatif. Contrairement à ce que l’on observe lorsque les hexagones sont utilisés, aucun effet négatif important sur la distance ne ressort entre 0 et 25 km. Plutôt, puisque la grande majorité des RTA sont petites et situées dans des régions métropolitaines, l’effet des flux sur de courtes distances est pris en compte par le terme pour la région et présente un coefficient positif élevé. Les hexagones, dont la répartition selon la taille n’est pas associée à la densité des flux sur de courtes distances, affichent une relation plus faible. Le fait de subdiviser davantage les effets de la distance sur les livraisons sur de courtes distances révèle une association positive pour la distance entre 0 et 10 km (modèle 3) et entre 0 et 5 km (modèle 4). À de si courtes distances, l’augmentation de la distance a peu d’effet sur les coûts des échanges, mais elle entraîne une augmentation apparente du nombre de sources potentielles de la demande. Les effets des frontières provinciales estimés sont inchangés lorsque ces changements sont apportés à la spécification. En bref, contrairement aux observations de Hillberry et Hummels (2008), l’adoption de très petites unités d’échanges n’élimine pas les effets de frontière. Par conséquent, les effets des frontières provinciales, bien que sensibles à la spécification et à la géographie, ne sont jamais éliminés. Toutefois, la question de savoir s’ils sont significatifs sur le plan économique reste entière.
5. Équivalent tarifaire de l’effet de frontière
Pour estimer l’équivalent tarifaire de l’effet des frontières provinciales, l’approche de Head et Mayer (2014, p. 32 à 34) est appliquée. Comme précédemment, indique le coefficient de l’effet des frontières provinciales, lequel reflète la réduction des coûts des échanges entre les régions infraprovinciales par le simple fait de faire partie de la même province. Puisque , où et sont les coûts des échanges interprovinciaux et intraprovinciaux, respectivement, et est l’élasticité des échanges en ce qui concerne les coûts de transport, si est le tarif qui doit être supprimé pour équivaloir le coût de déplacement des biens à l’intérieur des provinces et entre elles, l’équivalent tarifaire du commerce interprovincial est
où est l’équivalent tarifaire des obstacles au commerce à l’intérieur de la province, lesquels sont présumés être nuls. Par conséquent, la seule donnée manquante est l’élasticité du coût des échanges pour le commerce :
où est 1 plus les coûts de transport ad valorem, et sont, respectivement, les effets fixes du point d’origine et de destination et est le terme d’erreurs. Les coûts de transport ad valorem sont tirés du FTT, lequel indique le prix facturé aux expéditeurs et la valeur estimée de chaque livraison. L’élasticité des prix estiméeNote 13 en fonction de l’équation (8) est de -6,40, ce qui se situe entre la médiane (-5,03) et la moyenne (-6,74) des élasticités des prix indiquées dans la méta-analyse de Head et Mayer (2014).
Pour le coefficient médian de l’effet des frontières provinciales pour l’hexagone de 75 km de côté (figure 4, modèle 2), ou 6,9 %. Au moyen d’une méthodologie différente, Agnosteva, Anderson et Yotov (2014) arrivent à une estimation plus faible, mais statistiquement indiscernableNote 14, de 5,6 %.
Les équivalents tarifaires de l’effet de frontière parmi les unités géographiques normalisées et hexagonales sont présentés au graphique 1 et illustrent les répercussions de l’unité d’échanges choisie. Les hexagones utilisent les estimations ponctuelles médianes provenant des simulations présentées aux figures 3 et 4. Les estimations provinciales sont les plus élevées : elles se situent à 13,6 %. Elles sont suivies de près des équivalents tarifaires établis en fonction des RE et des DR, qui sont de 12,3 % et de 11,2 % respectivement. L’imposition d’une unité géographique hexagonale uniforme entraîne la baisse la plus notable du taux tarifaire. Au fur et à mesure que les hexagones deviennent plus grands, les estimations ponctuelles convergent vers un équivalent tarifaire de 7,3 %. L’équivalent tarifaire pour les hexagones de 75 km et de 225 km de côté qui tiennent compte de l’effet non linéaire de la distance et de la contiguïté (figure 4, modèle 2) produit les estimations les plus faibles, lesquelles sont essentiellement indiscernables. Par conséquent, dans le modèle entièrement spécifié, la taille de l’hexagone choisi n’entraîne que peu de conséquences. À 6,9 %, les hexagones de 75 km de côté produisent l’estimation privilégiée, en raison du plus petit écart interquartile par rapport aux hexagones de 225 km de côté. Comparativement à cette estimation, le fait de s’appuyer sur les échanges provinciaux augmenterait les estimations de l’effet de frontière de 6,7 points de pourcentage, une différence substantielle. Si on la replace dans son contexte, cette valeur est supérieure au taux tarifaire moyen du Canada (4,9 %)Note 15.
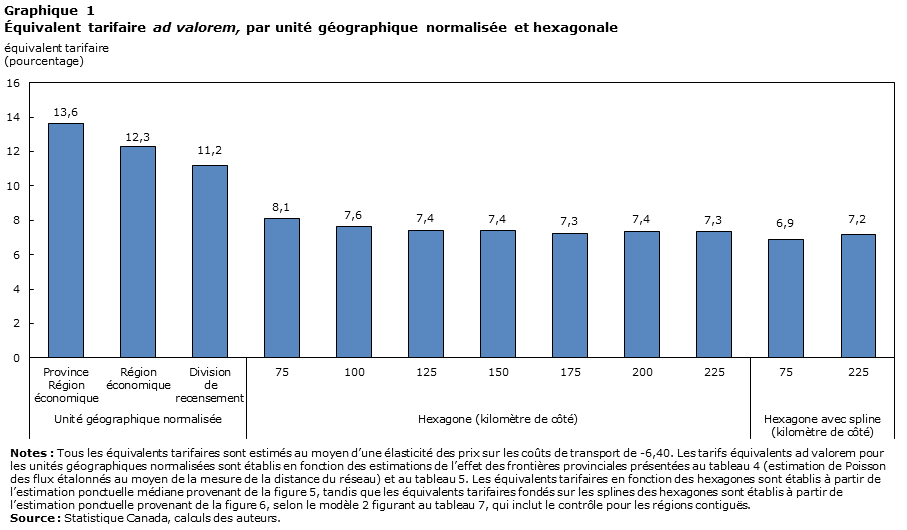
Tableau de données du graphique 1
| équivalent tarifaire | |
|---|---|
| valeur | |
| Unité géographique normalisée | |
| Province | 13,6 |
| Région économique | 12,3 |
| Division de recensement | 11,2 |
| Hexagone (kilomètre de côté) | |
| 75 | 8,1 |
| 100 | 7,6 |
| 125 | 7,4 |
| 150 | 7,4 |
| 175 | 7,3 |
| 200 | 7,4 |
| 225 | 7,3 |
| Hexagone avec spline (kilomètre de côté) | |
| 75 | 6,9 |
| 225 | 7,2 |
|
Notes : Tous les équivalents tarifaires sont estimés au moyen d’une élasticité des prix sur les coûts de transport de ‑6,40. Les tarifs équivalents ad valorem pour les unités géographiques normalisées sont établis en fonction des estimations de l’effet des frontières provinciales présentées au tableau 4 (estimation de Poisson des flux étalonnés au moyen de la mesure de la distance du réseau) et au tableau 5. Les équivalents tarifaires en fonction des hexagones sont établis à partir de l’estimation ponctuelle médiane provenant de la figure 5, tandis que les équivalents tarifaires fondés sur les splines des hexagones sont établis à partir de l’estimation ponctuelle provenant de la figure 6, selon le modèle 2 figurant au tableau 7, qui inclut le contrôle pour les régions contiguës. Source : Statistique Canada, calculs des auteurs. |
|
| Marchandise | Équivalent tarifaire |
|---|---|
| coefficient | |
| Grains et autres produits de récoltes | 0,07Note * |
| Animaux vivants | 0,09Note * |
| Poissons et fruits de mer, vivants, frais, réfrigérés ou congelés | -0,01 |
| Autres produits agricoles | 0,14Note * |
| Produits forestiers et services connexes | 0,32 |
| Minerais et concentrés de métaux | -0,23Note * |
| Minéraux non métalliques | 0,09 |
| Boissons alcoolisées et produits du tabac | 0,01 |
| Aliments et boissons non alcoolisées | 0,04Note * |
| Produits textiles, vêtements et produits en cuir et matériel similaire | 0,04Note * |
| Produits en bois | 0,12Note * |
| Pâte de bois, papier et produits en papier | 0,20Note * |
| Produits imprimés et services connexes | 0,07Note * |
| Produits raffinés du pétrole (sauf les produites pétrochimiques) | 0,02Note * |
| Produits chimiques | 0,02 |
| Produits en plastique et en caoutchouc | 0,08Note * |
| Produits minéraux non métalliques | 0,24Note * |
| Produits métalliques de première transformation | 0,06Note * |
| Produits métalliques usinés | 0,08Note * |
| Machinerie industrielle | 0,02Note * |
| Ordinateurs et produits électroniques | 0,01 |
| Matériel, appareils, et composants électriques | 0,02Note * |
| Pièces de véhicules à moteur | 0,11Note * |
| Matériel de transport | 0,03Note * |
| Meubles et produits connexes | 0,08Note * |
| Autres produits fabriqués et travail à forfait | 0,05Note * |
Source : Statistique Canada, calculs des auteurs. |
|
L’équivalent tarifaire de l’effet de frontière par marchandise est calculé en estimant l’effet de frontière par marchandise et l’élasticité des échanges par rapport aux coûts des transports . La signification statistique de l’effet de frontière est indiquée aux côtés du coefficient de l’équivalent tarifaire (tableau 9). L’effet de frontière est faible et statistiquement non significatif pour de nombreuses marchandises, notamment le matériel de transport, les machines industrielles et les produits pétroliers raffinés. Pour d’autres produits, qui sont en grande partie des biens intermédiaires (par exemple, les pièces de véhicules motorisés), un effet de frontière apparent ressort, reflétant potentiellement une variation de la demande industrielle entre les frontières provinciales. Par exemple, la majeure partie de la demande de pièces automobiles provient des usines d’assemblage concentrées en Ontario. Toutefois, pour d’autres marchandises, il peut y avoir un biais d’agrégation. Aucun effet de frontière significatif n’est observé pour les boissons alcoolisées et les produits du tabac, mais cela s’explique en grande partie par l’inclusion des produits du tabac. Lorsque les données sont désagrégées, la tendance attendue émerge : les équivalents tarifaires pour les boissons très alcoolisées, le vin et le brandy ainsi que la bière sont de 8 %, de 56 % et de 2 %Note 16, respectivement. Les produits laitiers pourraient être considérés de la même manière, mais les agrégations de marchandises dans les données de camionnage sont trop grandes pour décomposer les flux de produits laitiers afin d’estimer l’effet de frontière avec exactitude.
6. Conclusions
En raison d’un manque de données géographiquement détaillées sur le commerce à l’intérieur des provinces et entre elles, les effets des frontières intranationales sont difficiles à mesurer. En utilisant un nouveau fichier de données de transport flexible au niveau de la transaction pour générer des flux commerciaux régionaux à l’intérieur des provinces et entre elles, la présente analyse montre que peu importe le modèle ou l’unité géographique choisis, les effets des frontières provinciales se maintiennent, l’équivalent tarifaire ad valorem implicite s’établissant à 6,9 %. Cela contraste avec les estimations pour les États-Unis, où les effets des frontières entre les États sont éliminés lorsque des approches similaires sont appliquées. Bien que la présence d’effets des frontières provinciales concorde avec une certaine influence modératrice sur les obstacles non tarifaires au commerce interprovincial, elle ne rend pas compte, comme telle, de tous les obstacles, puisque les effets de frontière captent de multiples facteurs qui ont une incidence sur le commerce interprovincial.
Plusieurs observations fondées sur des méthodes peuvent être tirées de la présente analyse. Premièrement, bien que les résultats soient sensibles à la taille de l’unité géographique choisie (province, région économique, division de recensement ou hexagone), aucune relation linéaire simple n’existe entre la taille (moyenne) de l’unité géographique et les effets de frontière. En fait, la forme uniforme (hexagone) s’avère plus importante que la taille de l’unité géographique. Cela confirme la constatation d’Arbia (1989), selon laquelle les biais résultant de l’échelle et du zonage de l’unité géographique sont minimisés lorsqu’on utilise des unités identiques.
Deuxièmement, le fait tenir compte de l’effet non linéaire de la distance est tout aussi important, sinon plus, que le fait de contrôler l’unité géographique (problème d’unité spatiale modifiable MAUP). L’association négative entre la taille de l’hexagone et les effets de frontière découlant d’une relation non linéaire entre la distance et les échanges comme l’ont prédit Coughlin et Novy (2016) est effectivement éliminée lorsque ces non-linéarités sont explicitement prises en compte. Néanmoins, la prise en considération du MAUP demeure utile, puisque celui-ci fournit un moyen de tester la spécification du modèle.
D’autres travaux sont nécessaires afin de déterminer les effets des obstacles non tarifaires provinciaux sur les effets de frontière estimés parce qu’il est nécessaire de disposer de données directes sur l’ampleur de ces obstacles et sur d’autres facteurs qui ont une incidence sur le commerce interprovincial (par exemple, les liens solides et les flux migratoires entre les frontières provinciales). En outre, bien que l’analyse ait été en mesure d’estimer les effets des frontières provinciales, les conséquences sur le plan du bien-être général résultant de leur élimination ne sont pas mesurées dans la présente étude. Néanmoins, comme Albrecht et Tombe (2016) le démontrent, celles-ci peuvent être considérables.
Annexe A Annexe des données
A.1 Évaluation des livraisons
Les lettres de transport sur lesquelles le Fichier des transports terrestres (FTT) repose indiquent les marchandises et le tonnage de chaque livraison, mais pas sa valeur. Pour estimer la valeur, une mesure de la valeur par tonne est nécessaire. Cette mesure est extraite d’un fichier commercial expérimental au niveau de la transaction qui mesure la valeur et le tonnage des biens en fonction des marchandises détaillées dans le Système harmonisé de désignation et de codification des marchandises (SH) de 2008. Puisque le fichier commercial détermine le mode utilisé pour chaque livraison, la valeur par tonne pour chaque marchandise varie également selon le mode utilisé. Les indices des prix à l’exportation sont utilisés pour projeter les estimations de la valeur par tonne au fil du temps (voir Brown [2015] pour obtenir une description détaillée).
A.2 Géocodage des points d’origine et de destination des livraisons
Selon les données sur les codes postaux de l’Enquête sur l’origine et la destination des marchandises transportées par camion (ODMTC) et les codes unifiés des localités desservies provenant des bordereaux d’expéditions par chemin de fer, chaque livraison est géocodée (attribution d’une latitude et d’une longitude pour l’origine et la destination) de 2004 à 2012. Ces données sont utilisées pour générer une classification géographique type en date de 2006 (Statistique Canada, s.d.b). En conséquence, chaque point d’origine et de destination est codé par rapport à sa région économique (RE), à sa division de recensement (DR) et à sa subdivision de recensement unifiée (SRU). Avant 2004, l’Enquête ODMTC n’utilisait pas les codes postaux pour distinguer les points d’origine et de destination. Pour ces années, les flux sont codés uniquement relativement aux RE. Puisque la latitude et la longitude sont attribuées aux points d’origine et de destination, d’autres régions géographiques non normalisées peuvent être appliquées, comme les grilles hexagonales de la présente analyse. L’imputation d’un peu plus de la moitié des codes postaux seulement réduit probablement leur exactitude. Néanmoins, lorsqu’ils étaient cartographiés, les codes postaux imputés et non imputés présentaient des modèles géographiques semblables.
A.3 Poids de référence
L’un des principaux objectifs lors de la création du fichier est de faire en sorte que la valeur des échanges en fonction des livraisons dans le FTT s’ajoute aux totaux des échanges connus par marchandise provenant du fichier des flux du commerce interprovincial. Pour ce faire, deux problèmes doivent être surmontés, puisque les fichiers représentent des concepts commerciaux différents et qu’ils utilisent des classifications des marchandises également différentes.
Dans le fichier des flux du commerce interprovincial, l’origine représente un point de production et la destination représente un point de consommation. Toutefois, dans le FTT, l’origine représente le point où la livraison est ramassée et la destination représente le point où la livraison est déposée, et le fichier comprend notamment les entrepôts qui servent de points de cheminement pour le transport. Une marchandise fabriquée au Québec et consommée en Colombie-Britannique serait ainsi enregistrée comme un flux du Québec jusqu’à la Colombie-Britannique dans la base de données sur les flux du commerce interprovincial, mais ce flux peut avoir de multiples points d’origine et de destination dans le FTT si le produit passe par divers entrepôts dans différentes provinces en cours de livraison. Par exemple, un flux commercial du Québec à la Colombie-Britannique peut être enregistré comme un flux du Québec jusqu’à l’Ontario, puis comme un autre de l’Ontario jusqu’à la Colombie-Britannique. En conséquence, le FTT surestime les flux entre les provinces rapprochées et sous-estime les flux entre les provinces plus éloignées, ce qui peut biaiser à la hausse les effets de frontière. L’établissement de données repères est une tentative ayant pour but de repondérer les livraisons terrestres pour refléter le concept des flux du commerce interprovincial.
Les deux fichiers utilisent des systèmes de classification de marchandises connexes, mais différents en pratique. Bien que les deux systèmes de classification des marchandises soient conçus à partir du SH fondé sur les marchandises, les classifications agrégées qui en découlent sont suffisamment différentes pour entraîner l’élimination des correspondances biunivoques entre les deux. Le FTT utilise la classification type des biens transportés (CTBT) (Statistique Canada, s.d.a), tandis que le fichier des flux du commerce interprovincial utilise la Classification des produits par entrées-sorties (CPES). À tous les niveaux d’agrégation, certains codes de la CTBT correspondent à des codes de la CPES multiples, et vice versa. En raison du nombre élevé de correspondances multiples, on ne cherche pas à forcer un code de la CPES donné à correspondre à un code de la CTBT donné. L’objectif consiste plutôt à étalonner le FTT de manière à ce qu’il représente les mêmes valeurs que le fichier des flux interprovinciaux sans qu’il soit nécessaire de déterminer quelles marchandises transportées représentent quelles marchandises d’entrées-sorties. Plutôt que de tenter de forcer une correspondance biunivoque entre les fichiers, les poids de référence sont configurés de manière à ce que les flux s’ajoutent aux flux totaux de marchandises générés par le système des entrées-sorties. Ce processus comporte une série d’étapes.
À la première étape, chaque fichier est agrégé de manière à inclure les valeurs des flux par année, province d’origine, province de destination et type de marchandise (CTBT pour le FTT et CPES pour le fichier des flux commerciaux interprovinciaux). Cette agrégation génère deux vecteurs de la valeur des échanges commerciaux pour les flux de marchandises de la CPES et les flux de marchandises de la CTBT : et , respectivement.
À la deuxième étape, on établit une correspondance entre la CTBT et la CPES par paire de provinces et par année. À cette fin, on utilise des appariements « un à plusieurs » entre la CTBT et le SH et entre la CPES et le SH, qui sont ensuite combinés pour former un appariement « plusieurs à plusieurs » entre la CTBT et la CPES pour obtenir une matrice de concordance qui sera utilisée à la troisième et dernière étape.
À la dernière étape, les poids de référence sont calculés. Pour chaque année et chaque paire de provinces d’origine et de destination, les deux vecteurs de marchandises, et , sont combinés à la matrice de concordance , dans laquelle toutes les valeurs sont 0 ou 1 (selon qu’une marchandise de la CTBT donnée correspond à une marchandise de la CPES donnée). Si on définit le nombre de marchandises de la CPES comme et le nombre de marchandises de la CTBT comme , alors a une longueur , a une longueur et est une matrice . Le problème d’étalonnage peut être exprimé ainsi :
où est la matrice des valeurs d’étalonnage, et est le produit par élément de matrice (produit Hadamard). Toute qui permet de résoudre ce système d’équations étalonne selon à . Le problème consiste à trouver une solution aux équations sachant que est inconnu. Une solution classique consiste à forcer à être biunivoque de manière à ce que si , alors pour toutes les situations et pour toutes les situations , où et sont des composantes de . Ainsi, la matrice comporte uniquement des valeurs non nulles , et le poids de référence est . Dans ce cas, la concordance serait statique; il ne serait pas nécessaire d’établir une concordance par année, et encore moins par paire de provinces. Cependant, cette approche élimine des volumes considérables de renseignements relatifs aux relations commerciales sous-jacentes entre les provinces, puisque le profil des échanges de marchandises varie d’une paire de provinces à l’autre. Par exemple, les marchandises faisant l’objet d’un appariement forcé pourraient ne pas se trouver dans les échanges entre les deux provinces. Par conséquent, la concordance de référence doit refléter et en fait tirer parti de ces différences.
Afin de préserver l’information dans le contexte d’un problème de concordance « plusieurs à plusieurs » particulièrement difficile dans , chaque élément de est divisé en deux parties, , où :
L’équation (9) est le produit des parts commerciales des flux de la CTBT et de la CPES mis en concordance. On suppose que les flux de la CTBT et de la CPES constituent une représentation fidèle des tendances commerciales et qu’ils proposent des valeurs de référence appropriées. est la valeur permettant de résoudre l’équation
pour chaque équation dans le système, selon la convention voulant que si , ou que la somme du terme gauche de l’équation (10) est zéro. Il ne reste plus qu’à calculer une seule valeur de référence pour un code de la CTBT donné par
qui est considérée comme le poids de référence pour toutes les expéditions de marchandises de la CTBT pour cette année et cette paire de provinces d’origine et de destination. En d’autres mots, est la somme des valeurs de la colonne de .
Encore ici, toute valeur qui permet de résoudre cette équation sera une valeur de référence, mais on choisit de maximiser les renseignements fournis. Plus spécifiquement, on choisit pour utiliser la valeur d’un flux de marchandises de la CTBT relativement aux flux de la CTBT totaux qui pointe vers le même code de la CPES , et aussi pour utiliser la valeur du flux de ce code de la CPES relativement à tous les codes de la CPES vers lesquels pointe la marchandise de la CTBT . En outre, bien qu’il ne soit pas possible de comparer deux marchandises directement, la valeur totale des échanges commerciaux de référence est identique à la valeur totale des échanges interprovinciaux (pour chaque observation année-province-année), puisque
Ainsi, la procédure permet d’atteindre l’objectif ultime, c’est-à-dire que la somme des flux commerciaux soit égale à des totaux connus extraits des comptes provinciaux.
Dans certaines situations, l’échantillon des expéditions n’englobera pas l’ensemble des marchandises de la CTBT entre deux provinces au cours d’une année donnée (figure 1 à la sous-section 2.1). Dans la présente situation, pour certaines marchandises de la CPES , l’élément du vecteur est zéro parce que pour toutes les marchandises possibles qui correspondent à (celles pour lesquelles ). Dans ce cas, l’élément est inclus dans le total des échanges interprovinciaux, mais la valeur correspondante est zéro pour le terme droit de l’équation, ce qui signifie que le total des échanges dans le FTT est inférieur au total des échanges dans les flux interprovinciaux,
Finalement, dans le corps principal du texte, l’indice est supprimé de sorte que le poids de référence est .
A.4 Comparaison entre les distances du réseau et les distances orthodromiques intraprovinciales et interprovinciales
L’analyse repose sur la distance du réseau entre les points d’origine et de destination géocodés, ce qui correspond aux distances intraprovinciales et interprovinciales moyennes au niveau de la transaction. Traditionnellement, les distances intraprovinciales et interprovinciales sont calculées au moyen de la distance orthodromique origine-destination, pondérée selon la population (ci-après, la distance orthodromique), entre les unités infraprovinciales (voir, par exemple, Brown et Anderson, 2002). Cette distance est calculée pour l’ensemble des unités infraprovinciales (DR) à l’intérieur de chaque province pour le commerce intraprovincial et entre les ensembles d’unités infraprovinciales pour chaque paire de provinces :
où et répertorient les provinces, et répertorient les DR, est la population de la DR, et correspond à la distance orthodromique entre les centroïdes des DR. Pour le commerce intraprovincial , la distance à l’intérieur des DR correspond au rayon d’un cercle d’une superficie égale à celle de la DR : .
On peut supposer que la distance du réseau surpasse toujours celle de la distance orthodromique. Toutefois, puisque la distance (du réseau) réellement parcourue est biaisée en faveur des déplacements sur de courtes distances, lorsque ceux-ci sont plus fréquents (par exemple, pour le commerce intraprovincial ou le commerce entre des provinces contiguës), la distance du réseau mesurée peut s’avérer plus courte que la distance orthodromique. Autrement dit, pour la distance orthodromique, lorsqu’on maintient la population constante, la distance entre les paires de DR rapprochées est pondérée de la même façon qu’entre les DR plus éloignées. Ainsi, puisqu’elles sont extraites à partir de déplacements réels, les estimations de la distance du réseau pour les paires de RD rapprochées auront un poids plus élevé.
Cette tendance est évidente dans les données présentées au tableau A.1, qui présente la distance du réseau et la distance orthodromique à l’intérieur des provinces et entre elles. En moyenne, la distance du réseau est de 33 % plus grande que la distance orthodromique. Toutefois, cela reflète la tendance des distances intraprovinciales et de celles entre les provinces contiguës à être plus près de la distance du réseau (ou parfois moindres). La distance du réseau, à l’intérieur de la province, entre les provinces contiguës et entre les provinces non contiguës, est plus élevée de 9 %, 25 % et 38 % que la distance orthodromique, respectivement. Les provinces de l’Atlantique, qui forment un archipel de facto et dont les distances du réseau interne surpassent naturellement les distances orthodromiques par une large marge (tableau A.1), sont l’exception.
Deux implications pour l’analyse économétrique découlent de ces tendances liées à la distance. Premièrement, puisque la distance orthodromique est moindre que la distance de réseau, l’élasticité de la distance sera moins grande lorsque la distance du réseau est utilisée. Deuxièmement, les distances orthodromiques intraprovinciales relativement plus courtes auront tendance à gonfler le coefficient de commerce intraprovincial (effet de frontière), puisque le commerce intraprovincial est surestimé en raison de la distance réelle parcourue. Les deux effets sont apparents dans les estimations.
| T.-N.-L. | Î.-P.-É. | N.-É. | N.-B. | Qc | Ont. | Man. | Sask. | Alb. | C.-B. | |
|---|---|---|---|---|---|---|---|---|---|---|
| kilomètres | ||||||||||
| Élément A — Distance du réseau | ||||||||||
| Terre-Neuve-et-Labrador | 386 | 1 364 | 1 226 | 1 344 | 1 567 | 2 789 | 4 650 | 5 223 | 6 074 | 6 902 |
| Île-du-Prince-Édouard | 1 412 | 61 | 333 | 272 | 1 115 | 1 706 | 3 584 | 4 209 | 4 810 | 5 696 |
| Nouvelle-Écosse | 1 326 | 324 | 136 | 389 | 1 173 | 1 815 | 3 616 | 4 308 | 4 977 | 5 802 |
| Nouveau-Brunswick | 1 359 | 240 | 396 | 153 | 692 | 1 357 | 3 293 | 3 946 | 4 588 | 5 307 |
| Québec | 1 478 | 1 095 | 1 222 | 728 | 280 | 584 | 2 459 | 3 114 | 3 734 | 4 607 |
| Ontario | 2 818 | 1 730 | 1 819 | 1 456 | 599 | 191 | 2 026 | 2 798 | 3 429 | 4 320 |
| Manitoba | 4 573 | 3 526 | 3 627 | 3 236 | 2 410 | 1 707 | 213 | 654 | 1 340 | 2 207 |
| Saskatchewan | 5 249 | 4 127 | 4 322 | 3 929 | 3 118 | 2 692 | 621 | 221 | 683 | 1 570 |
| Alberta | 5 806 | 4 907 | 4 908 | 4 578 | 3 720 | 3 248 | 1 316 | 660 | 219 | 905 |
| Colombie-Britannique | 6 873 | 5 750 | 5 872 | 5 476 | 4 640 | 4 283 | 2 244 | 1 631 | 1 010 | 204 |
| Élément B — Distance orthodromique | ||||||||||
| Terre-Neuve-et-Labrador | 261 | 715 | 762 | 894 | 1 407 | 1 987 | 3 056 | 3 539 | 4 056 | 4 717 |
| Île-du-Prince-Édouard | 715 | 39 | 193 | 211 | 756 | 1 322 | 2 547 | 3 071 | 3 621 | 4 274 |
| Nouvelle-Écosse | 762 | 193 | 143 | 290 | 805 | 1 344 | 2 635 | 3 167 | 3 723 | 4 374 |
| Nouveau-Brunswick | 894 | 211 | 290 | 140 | 578 | 1 134 | 2 377 | 2 909 | 3 464 | 4 115 |
| Québec | 1 407 | 756 | 805 | 578 | 208 | 615 | 1 893 | 2 442 | 3 010 | 3 648 |
| Ontario | 1 987 | 1 322 | 1 344 | 1 134 | 615 | 226 | 1 541 | 2 107 | 2 688 | 3 292 |
| Manitoba | 3 056 | 2 547 | 2 635 | 2 377 | 1 893 | 1 541 | 145 | 604 | 1 173 | 1 780 |
| Saskatchewan | 3 539 | 3 071 | 3 167 | 2 909 | 2 442 | 2 107 | 604 | 234 | 628 | 1 233 |
| Alberta | 4 056 | 3 621 | 3 723 | 3 464 | 3 010 | 2 688 | 1 173 | 628 | 221 | 709 |
| Colombie-Britannique | 4 717 | 4 274 | 4 374 | 4 115 | 3 648 | 3 292 | 1 780 | 1 233 | 709 | 213 |
| pourcentage | ||||||||||
| Élément C — Différence entre la distance du réseau et la distance orthodromique | ||||||||||
| Terre-Neuve-et-Labrador | 48 | 91 | 61 | 50 | 11 | 40 | 52 | 48 | 50 | 46 |
| Île-du-Prince-Édouard | 98 | 59 | 72 | 29 | 47 | 29 | 41 | 37 | 33 | 33 |
| Nouvelle-Écosse | 74 | 67 | -5 | 34 | 46 | 35 | 37 | 36 | 34 | 33 |
| Nouveau-Brunswick | 52 | 14 | 37 | 9 | 20 | 20 | 39 | 36 | 32 | 29 |
| Québec | 5 | 45 | 52 | 26 | 34 | -5 | 30 | 28 | 24 | 26 |
| Ontario | 42 | 31 | 35 | 28 | -3 | -15 | 31 | 33 | 28 | 31 |
| Manitoba | 50 | 38 | 38 | 36 | 27 | 11 | 47 | 8 | 14 | 24 |
| Saskatchewan | 48 | 34 | 36 | 35 | 28 | 28 | 3 | -6 | 9 | 27 |
| Alberta | 43 | 36 | 32 | 32 | 24 | 21 | 12 | 5 | -1 | 28 |
| Colombie-Britannique | 46 | 35 | 34 | 33 | 27 | 30 | 26 | 32 | 43 | -5 |
| Source : Statistique Canada, calculs des auteurs. | ||||||||||
Annexe B Vérifications de la robustesse
B.1 Contrôle de l’effet différentiel sur la distance pour le commerce intraprovincial et interprovincial
Si le commerce intraprovincial comporte un grand ensemble de flux logistiques tronqués, le paramètre de la distance pour les flux intraprovinciaux devrait être plus négatif que celui pour les flux interprovinciaux, dont la structure découle de l’étalonnage des flux des comptes entrées-sorties provinciaux. Pour vérifier cet effet, une version modifiée de l’équation (5) est estimée,
Le paramètre de la distance peut varier entre les flux intraprovinciaux et interprovinciaux au moyen d’une variable indicatrice pour les flux intraprovinciaux Note 17. Si l’effet de troncature prédomine, le paramètre de la distance pour le commerce intraprovincial devrait être plus négatif que celui pour le commerce interprovincial. Pour isoler cet effet, le modèle est estimé au moyen d’effets fixes distincts pour le point d’origine et de destination pour le commerce intraprovincial et interprovincial, où indique l’ensemble des régions intraprovinciales. Les flux intrarégionaux sont exclusNote 18. Lorsqu’il était estimé au niveau de la RE, le paramètre de la distance était de -0,769 pour le commerce interprovincial, mais significativement moins négatif pour le commerce intraprovincial (-0,601) . Lorsqu’il était estimé au niveau de la DR, une sous-unité de la RE, il n’y avait pas de différence significative entre les paramètres de la distance pour le commerce intraprovincial . Dans la mesure où elle est présente, la troncature des flux intraprovinciaux ne semble pas suffisante pour biaiser les estimations.
B.2 Estimations par année
Les estimations sont présentées pour la moyenne des échanges répartie sur la période d’étude de neuf ans allant de 2004 à 2012. Cette période est suffisamment longue pour observer des changements découlant d’initiatives stratégiques ou de changements au sein de la macroéconomie. Pour tenir compte de ces effets, le modèle de base a été estimé avec toutes les variables interagissant avec les effets fixes dans le temps (l’année 2004 étant exclue). Que le modèle soit estimé sur la base des provinces, des RE ou des DR comme unités d’échanges, aucune différence significative dans les coefficients n’a été observée au fil des ans (tableau B.1). Par conséquent, les estimations fondées sur le niveau des échanges moyen rapporté dans le contenu principal du présent document dressent un portrait raisonnable de l’effet des frontières provinciales sur toute la période.
| Province | Unité géographique | ||
|---|---|---|---|
| Région économique | Division de recensement | ||
| Dans la province | |||
| Coefficient | 0,756Note ** | 0,752Note ** | 0,747Note ** |
| Erreur-type | 0,113 | 0,128 | 0,093 |
| 2005 | |||
| Coefficient | -0,021 | 0,027 | 0,072 |
| Erreur type | 0,149 | 0,194 | 0,150 |
| 2006 | |||
| Coefficient | -0,0449 | 0,0256 | 0,0595 |
| Erreur-type | 0,143 | 0,180 | 0,134 |
| 2007 | |||
| Coefficient | 0,0548 | 0,1170 | 0,1170 |
| Erreur-type | 0,144 | 0,189 | 0,128 |
| 2008 | |||
| Coefficient | 0,028 | 0,128 | 0,146 |
| Erreur-type | 0,151 | 0,187 | 0,145 |
| 2009 | |||
| Coefficient | -0,0173 | -0,0310 | -0,0495 |
| Erreur-type | 0,158 | 0,173 | 0,131 |
| 2010 | |||
| Coefficient | 0,0663 | 0,1470 | 0,0619 |
| Erreur-type | 0,180 | 0,196 | 0,134 |
| 2011 | |||
| Coefficient | 0,0192 | -0,0619 | -0,1420 |
| Erreur-type | 0,174 | 0,190 | 0,132 |
| 2012 | |||
| Coefficient | 0,2630 | -0,0598 | -0,1030 |
| Erreur-type | 0,248 | 0,171 | 0,127 |
| Valeur R au carré | 0,875 | 0,721 | 0,983 |
| Nombre d’observations | 900 | 47 961 | 713 480 |
Source : Statistique Canada, calculs des auteurs. |
|||
B.3 Estimations différentielles des effets de frontière pour le Québec
Pour vérifier les effets du Québec sur le commerce intérieur, on a fait interagir la province avec une variable indicatrice pour les flux commerciaux internes du Québec. Bien que l’estimation ponctuelle sur le paramètre d’interaction soit positive, elle n’est pas significativement différente de zéro (tableau B.2).
| Distance | Estimations |
|---|---|
| 0 km à 25 km | |
| Coefficient | -0,931Note *** |
| Erreur-type | 0,122 |
| 25 km à 100 km | |
| Coefficient | -0,273 |
| Erreur-type | 0,225 |
| 100 km à 500 km | |
| Coefficient | -0,803Note *** |
| Erreur-type | 0,092 |
| Plus de 500 km | |
| Coefficient | -0,877Note ** |
| Erreur-type | 0,066 |
| Dans la région | |
| Coefficient | 0,176 |
| Erreur-type | 0,198 |
| Dans la province | |
| Coefficient | 0,346Note *** |
| Erreur-type | 0,0844 |
| Dans la province × Québec | |
| Coefficient | 0,244 |
| Erreur-type | 0,209 |
| Régions contigües | |
| Coefficient | -0,139 |
| Erreur-type | 0,097 |
| Constante | |
| Coefficient | 2,819Note ** |
| Erreur-type | 0,503 |
| Nombre d’observations | 132 862 |
Source : Statistique Canada, calculs des auteurs. |
|
Bibliographie
Agnosteva, D.E., J.E. Anderson, et Y.V. Yotov. 2014. Intra-national Trade Costs: Measurement and Aggregation. NBER Working Papers no 19872. Cambridge, Massachusetts : National Bureau of Economic Research.
Albrecht, L., et T. Tombe. 2016. « Internal trade, productivity, and interconnected industries: A quantitative analysis ». Revue canadienne d’économique 49 (1).
Amrhein, C.G. 1995. « Searching for the elusive aggregation effect: Evidence from statistical simulation ». Environment and Planning A 27 (1) : 105 à 119.
Amrhein, C.G., et R. Flowerdew. 1992. « The effect of data aggregation on a Poisson regression model of Canadian migration ». Environment and Planning A 24 (10) : 1381 à 1391.
Anderson, J.E. 2010. The Gravity Model. NBER Working Papers no 16576. Cambridge, Massachusetts : National Bureau of Economic Research.
Anderson, J.E., et E. van Wincoop. 2003. « Gravity with gravitas: A solution to the border puzzle ». American Economic Review 93 (1) : 170 à 192.
Anderson, J.E., et Y.V. Yotov. 2010. « The changing incidence of geography ». American Economic Review 100 (5) : 2157 à 2186.
Anderson, J.E., et Y.V. Yotov. 2012. Gold Standard Gravity. NBER Working Papers, no 17835. Cambridge, Massachusetts : National Bureau of Economic Research.
Arbia, G. 1989. Spatial Data Configuration in Statistical Analysis of Regional Economic and Related Problems. Dordrecht, Pays-Bas : Kluwer Academic Publishers.
Baldwin, J.R., et W. Gu. 2009. « The impact of trade on plant scale, production-run length and diversification ». Dans Producer Dynamics: New Evidence from Micro Data, publié sous la direction de T. Dunne, J.B. Jensen, et M. Roberts, vol. : 68 de Studies in Income and Wealth. National Bureau of Economic Research. Chicago : University of Chicago Press.
Behrens, K., T. Bougna, et W.M. Brown. 2015. The World Is Not Yet Flat: Transportation Costs Matter! CEPR Discussion Paper no. 10356. London : Centre for Economic Policy Research.
Briant, A., P.-P. Combes, et M. Lafourcade. 2010. « Dots to boxes: Do the size and shape of spatial units jeopardize economic geography estimations? ». Journal of Urban Economics 67 (3) : 287 à 302.
Brown, W.M. 2003. Vaincre les distances, vaincre les frontières : comparaison des échanges régionaux en Amérique du Nord. Série de documents de recherche sur l’analyse économique, no 8. Produit no 11F0027M au catalogue de Statistique Canada. Ottawa : Statistique Canada.
Brown, W.M. 2015. « How much thicker is the Canada–U.S. border? The cost of crossing the border by truck in the pre- and post-9/11 eras ». Research in Transportation Business and Management 16 : 50 à 56.
Brown, W.M., et W.P. Anderson. 2002. « Spatial markets and the potential for economic integration between Canadian and U.S. regions ». Papers in Regional Science 81 (1) : 99 à 120.
Coughlin, C.C., et D. Novy. 2016. Estimating Border Effects: The Impact of Spatial Aggregation. Federal Reserve Bank of St. Louis Working Paper Series, no. 2016-006A. St. Louis, Missouri : Federal Reserve Bank of St. Louis.
Crafts, N., et A. Klein. 2015. « Geography and intra-national home bias: U.S. domestic trade in 1949 and 2007 ». Journal of Economic Geography 15 (3) : 477 à 497.
Fally, T. 2015. « Structural gravity and fixed effects ». Journal of International Economics 97 (1) : 76 à 85.
Fotheringham, A.S., et M.E. O’Kelly. 1989. Spatial Interaction Models: Formulations and Applications. Dordrecht, Pays-Bas : Kluwer Academic Publishers.
Fotheringham, A.S., et D.W.S. Wong. 1991. « The modifiable areal unit problem in multivariate statistical analysis ». Environment and Planning A 23 (7) : 1025 à 1044.
Généreux, P.A., et B. Langen. The Derivation of Provincial (Inter-regional) Trade Flows: The Canadian Experience. Paper presented at the 14th International Input-Output Techniques Conference, Montréal, 10 au 15 octobre 2002.
Head, K., et T. Mayer. 2010. « Illusory border effects: Distance mismeasurement inflates estimates of home bias in trade ». Dans The Gravity Model in International Trade: Advances and Applications, publié sous la direction de P.A.G. van Bergeijk et S. Brakman, chapitre 6, p. 165 à 192. Cambridge : Cambridge University Press.
Head, K., et T. Mayer. 2013. « What separates us? Sources of resistance to globalization ». Revue canadienne d’économique 46 (4) : 1196 à 1231.
Head, K., et T. Mayer. 2014. « Gravity equations: Workhorse, toolkit, and cookbook ». Dans Handbook of International Economics, publié sous la direction de G. Gopinath, E. Helpman, et K. Rogoff, vol. 4, chapitre 3, p. 131 à 195. Amsterdam : North Holland.
Hillberry, R., et D. Hummels. 2003. « Intranational home bias: Some explanations ». Review of Economics and Statistics 85 (4) : 1089 à 1092.
Hillberry, R., et D. Hummels. 2008. « Trade responses to geographic frictions: A decomposition using micro-data ». European Economic Review 52 (3) : 527 à 550.
Manning, W., et J. Mullahy. 2001. « Estimating log models: To transform or not to transform? ». Journal of Health Economics 20 (4) : 461 à 494.
McCallum, J. 1995. « National borders matter: Canada–U.S. regional trade patterns ». American Economic Review 85 (3) : 615 à 623.
Melitz, M.J., et G.I.P. Ottaviano. 2008. « Market size, trade and productivity ». Review of Economic Studies 75 (1) : 295 à 316.
Millimet, D.L., et T. Osang. 2007. « Do state borders matter for U.S. intranational trade? The role of history and internal migration ». Revue canadienne d’économique 40 (1) : 93 à 126.
Páez, A., et D.M. Scott. 2005. « Spatial statistics for urban analysis: A review of techniques with examples ». GeoJournal 61 (1) : 53 à 67.
Santos Silva, J.M.C., et S. Tenreyro. 2006. « The log of gravity ». Review of Economics and Statistics 88 (4) : 641 à 658.
Sen, A., et T. Smith. 1995. Gravity Models of Spatial Interaction Behavior. Berlin : Springer.
Statistique Canada, s.d.a. Classification type des biens transportés (CTBT) 1996. Dernière mise à jour le 17 avril 2015. Disponible au lien suivant : http://www.statcan.gc.ca/fra/sujets/norme/ctbt/ctbtmenu (consulté le 26 janvier 2017).
Statistique Canada, s.d.b. Classification géographique type (CGT) 2006 - Volume I La classification. Dernière mise à jour le 30 janvier 2017. Archivé. Disponible au lien suivant : http://www.statcan.gc.ca/fra/sujets/norme/cgt/2006/2006-ind-fin (consulté le 8 février 2017).
Wolf, H.C. 2000. « Intranational Home Bias in Trade ». Review of Economics and Statistics 82 (4) : 555 à 563.
Groupe de la Banque mondiale. 2016. Taux des droits de douane, nation la plus favorisée, moyenne simple, tous produits (%) (Graphique et tableau donnant un aperçu par pays). Données annuelles de 1996 à 2012. Disponible au lien suivant : http://donnees.banquemondiale.org/indicateur/TM.TAX.MRCH.SM.FN.ZS (consulté le 17 janvier 2017).
- Date de modification :