Direction des études analytiques : documents de recherche
Transmission intergénérationnelle du revenu : nouvelles données pour le Canada
 Consulter la version la plus récente.
Consulter la version la plus récente.
Information archivée dans le Web
L’information dont il est indiqué qu’elle est archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Elle n’est pas assujettie aux normes Web du gouvernement du Canada et elle n’a pas été modifiée ou mise à jour depuis son archivage. Pour obtenir cette information dans un autre format, veuillez communiquer avec nous.
par Wen-Hao Chen et Yuri Ostrovsky, Division de l'analyse sociale et de la modélisation, Statistique Canada
et Patrizio Piraino, Université de Cape Town, Afrique du Sud
Remerciements
Les auteurs tiennent à remercier Miles Corak pour ses observations très détaillées et pertinentes à propos d'une version antérieure de l'article. Les opinions exprimées sont celles des auteurs et ne représentent pas forcément les points de vue de Statistique Canada. Toute erreur est la seule responsabilité des auteurs.
Résumé
La présente étude fait appel à une version actualisée d'un ensemble unique de données administratives pour le Canada afin de déterminer l'incidence de la variation des gains au cours du cycle de vie et du biais lié aux erreurs dans les variables sur les estimations de l'élasticité intergénérationnelle du revenu. Les résultats révèlent des niveaux supérieurs de la persistance intergénérationnelle des gains et du revenu par rapport aux études antérieures. Le biais lié au cycle de vie dans les estimations antérieures explique près des deux tiers de la divergence, alors que le biais lié aux erreurs dans les variables rend compte de l'autre tiers. L'étude montre que ces biais ont une moins grande incidence sur les filles que sur les fils. On utilise également l'ensemble de données amélioré pour réexaminer les tendances non linéaires de la transmission intergénérationnelle du revenu au Canada. Les résultats donnent à penser que la mobilité limitée dans les segments supérieurs de la répartition explique la majeure partie de la persistance du revenu moyen au fil des générations, alors que l'on constate une mobilité considérablement plus élevée chez les enfants de pères à faible revenu. Une comparaison des résultats de l'analyse avec ceux d'études réalisées dans d'autres pays révèle que les tendances non linéaires observées au Canada sont quelque peu différentes de celles que l'on observe aux États-Unis et se rapprochent des tendances constatées dans les pays de l'Europe du Nord.
Classification du Journal of Economic Literature : J62, D31, D63
Mots-clés : inégalité des gains, mobilité intergénérationnelle
Sommaire
Dans le cadre des études comparatives de la mobilité intergénérationnelle des gains et du revenu, le Canada se classe généralement comme l'un des pays les plus mobiles parmi les économies avancées comme le Danemark, la Finlande et la Norvège. L'affirmation selon laquelle le Canada est une société hautement mobile est fondée sur les estimations de l'élasticité intergénérationnelle du revenu dont font état Corak et Heisz (1999). Corak et Heisz ont utilisé les données d'une version antérieure de la base de données sur la mobilité intergénérationnelle du revenu (base de DMIR), qui fait le suivi du revenu des jeunes Canadiens uniquement jusqu'au début de la trentaine. Des publications théoriques récentes proposent toutefois que la relation entre le revenu à vie des enfants et celui des parents ne peut pas être estimée avec exactitude si l'on n'observe pas le revenu des enfants à la mi-carrière. C'est ce qu'on appelle le biais lié au cycle de vie.
La présente étude se penche sur cette question en réexaminant l'importance de la mobilité intergénérationnelle des gains et du revenu au Canada à l'aide d'une version actualisée de la base de DMIR qui fait le suivi des enfants jusqu'à la mi-quarantaine avancée, ce qui permet d'observer le revenu à la mi-carrière. Ces renseignements sont cruciaux pour une analyse intergénérationnelle; les ouvrages publiés montrent que le biais découlant de la variation liée au cycle de vie peut être considérablement atténué si l'on compare les gains des pères à ceux de leurs enfants à un âge proche de la mi-carrière. L'étude examine aussi la divergence de la mobilité intergénérationnelle au sein de la population. Grâce à près de 250 000 observations, l'étude permet de déterminer le degré de transmission intergénérationnelle d'un bout à l'autre de la répartition du revenu.
L'analyse empirique réalisée dans le cadre de l'étude est fondée sur la base de DMIR de Statistique Canada, qui a été constituée à partir de divers fichiers d'impôt afin de coupler les enfants et leurs parents. La base de DMIR comprend des données sur les jeunes qui étaient âgés de 16 à 19 ans en 1982 et dont les données de l'impôt ont pu être couplées à celles de leurs parents grâce aux numéros d'assurance sociale des parents et des enfants et aux données du fichier sur la famille T1 de Statistique Canada. Les données portent sur plus de 20 années de gains pour les parents (1978 à 1999) et les enfants (1986 à 2008) aux fins de comparaison du revenu des enfants et des parents à l'étape principale de leur cycle de vie.
Les résultats de l'analyse montrent encore que le Canada est une société mobile, mais pas dans la mesure où on le croyait. La nouvelle estimation de l'élasticité des gains de père en fils s'établit à environ 0,32, une valeur sensiblement supérieure à celles qui ont été rapportées dans les ouvrages publiés (qui s'établissaient autour de 0,2); le biais lié au cycle de vie explique à lui seul environ les deux tiers de la divergence entre les premières estimations et le nouveau résultat. La persistance intergénérationnelle tend à être plus élevée lorsque le revenu du marché (c.-à-d. la somme des gains et des revenus d'un travail indépendant et de placements) est mesuré. Cela semble indiquer que d'autres mécanismes, comme la transmission des emplois ou des aptitudes entrepreneuriales, pourraient intervenir. Fait intéressant à souligner, l'analyse montre aussi que l'élasticité père-fille est beaucoup moins sensible à ces biais. En outre, l'article décrit une tendance claire de non-linéarité en ce qui concerne la transmission intergénérationnelle des gains et du revenu au Canada. Plus particulièrement, le chemin vers le sommet de la répartition semble particulièrement difficile pour les fils de pères à faible revenu. En revanche, il semble que ces mêmes fils avaient une forte probabilité d'atteindre la classe moyenne. Les institutions sociales pourraient entre autres expliquer cette dernière constatation. Enfin, le présent article montre que la tendance de non-linéarité peut être très mal interprétée si le biais lié au cycle de vie n'est pas pris en compte comme il se doit, particulièrement dans la partie supérieure de la répartition.
1 Introduction
Dans le cadre des études comparatives de la mobilité intergénérationnelle des gains et du revenu, le Canada est considéré généralement comme l'un des pays les plus mobiles parmi les économies avancées (Björklund et Jäntti, 2010; Corak, 2013; Solon, 2002). On a souvent recours à un graphique connu, que l'on appelle la « courbe de Gatsby le Magnifique », pour illustrer la relation entre l'inégalité du revenu et la mobilité sociale; selon ce graphique, le Canada est l'un des pays ayant la mobilité la plus élevée et se compare à cet égard au Danemark, à la Finlande et à la NorvègeNote 1. L'affirmation selon laquelle le Canada est une société hautement mobile est fondée principalement sur les estimations de l'élasticité intergénérationnelle du revenu (EIR) dont font état Corak et Heisz (1999) ainsi que Fortin et Lefebvre (1998). Bien que ces études minutieuses offrent les meilleures estimations de l'EIR en fonction des données disponibles au moment de leur réalisation, des ouvrages récents indiquent que ces estimations pourraient être biaisées en raison, surtout, de la variation liée au cycle de vie (Mazumder, 2005; Haider et Solon, 2006; Böhlmark et Lindquist, 2006).
En l'absence de données sur les gains à vie, les estimations de l'EIR peuvent être influencées par des erreurs de mesure dans les deux membres de l'équation. Un biais lié au cycle de vie peut se produire dans l'analyse de la mobilité entre père et enfant lorsque les gains permanents de l'enfant, calculés par approximation des gains annuels ou moyens sur une courte période, sont observés à une étape de la vie active de l'enfant où les gains ne se rapprochent pas beaucoup de ceux que l'enfant touchera au cours de sa vie. Haider et Solon (2006) ont montré que ce type de biais entraîne généralement des estimations plus faibles de l'EIR lorsqu'on utilise les gains de début (ou de fin) de vie active. Cette constatation correspond à ce que l'on trouve dans les ouvrages publiés, qui montrent que les estimations les plus faibles de l'EIR figurent souvent dans des études où les gains des fils sont observés à des âges moins avancés (Solon, 1999). C'est également évident pour Corak et coll. (2014), qui constatent que l'estimation de l'EIR pour le Canada augmente, pour passer de 0,22 à 0,26, lorsque les gains des fils sont observés à 35 ans au lieu de 30 ans, ce qui donne à penser que les effets du cycle de vie ne devraient pas non plus être ignorés au CanadaNote 2.
En plus du biais lié au cycle de vie, les estimations de l'EIR pourraient aussi être influencées par le biais classique lié aux erreurs dans les variables (erreur de mesure dans le second membre de l'équation), qui se produit lorsque les gains à vie des pères ne sont pas mesurés comme il se doit. Corak et Heisz (1999), par exemple, ont remédié à ce problème en utilisant une moyenne sur cinq ans, plutôt que les gains d'une seule année pour obtenir une mesure indirecte des gains à vie du père. Bien qu'une telle pratique réduise le biais lié aux erreurs dans les variables, elle ne l'élimine pas nécessairement en entier si le nombre d'années utilisé pour calculer les moyennes n'est pas assez élevé. Mazumder (2005) a montré que même des estimations fondées sur les gains moyens sur une période de cinq ans peuvent présenter un biais important lié aux erreurs dans les variables.
L'objectif principal de la présente étude est donc de réexaminer l'importance de la mobilité intergénérationnelle des gains et du revenu au Canada en tenant compte des problèmes d'estimation soulevés dans les ouvrages publiés à ce sujet. À l'aide de données longitudinales sur les gains d'un nombre d'années considérablement supérieur à celui de l'étude antérieure, la présente analyse fait ressortir la sensibilité des estimations de l'EIR aux biais liés au cycle de vie et aux erreurs dans les variables et surtout, elle passe en revue la question de la non-linéarité dans la transmission intergénérationnelle des gains. Des mesures améliorées des gains permanents des pères et des enfants pourraient avoir une incidence différente sur la persistance intergénérationnelle estimée dans différents segments de la répartition. On emploie des spécifications de régression polynomiale et quantile pour étudier cette possibilité. Grâce à près de 250 000 observations, il est possible d'examiner les différences dans le degré de mobilité intergénérationnelle d'un bout à l'autre de la répartition du revenu.
L'analyse empirique est fondée sur une version augmentée de la base de données sur la mobilité intergénérationnelle du revenu (base de DMIR), un ensemble de données de qualité supérieure couplant les données administratives des parents et des enfants au Canada. Grâce à ces données, il est possible d'introduire deux nouveaux éléments essentiels qui ne se trouvaient pas dans les études antérieures. D'abord, la base de DMIR mise à jour contient les données d'un échantillon exceptionnellement grand par rapport aux versions antérieures, en plus d'offrir des données fiscales couvrant une période beaucoup plus longue pour les enfants, lesquels peuvent maintenant être observés depuis la fin de l'adolescence jusqu'à la mi-quarantaine avancée. Ces renseignements sont essentiels pour vérifier l'incidence du biais lié au cycle de vie sur les estimations de l'EIR, les études publiées montrant que ce biais peut être considérablement atténué si l'on compare les gains des pères avec ceux de leurs enfants à l'approche de la mi-carrière (Grawe, 2006; Haider et Solon, 2006; Gouskova, Chiteji et Stafford, 2010). Ensuite, au lieu d'établir une moyenne du revenu sur une période arbitraire du calendrier, on calcule la moyenne pour une fourchette d'âge particulière. Comme on dispose de données valides sur une période allant jusqu'à 22 ans, le revenu à vie des pères est estimé en calculant la moyenne du revenu gagné de 35 à 55 ans. Cette méthode devrait réduire considérablement, voire éliminer, le biais d'atténuation découlant des erreurs de mesure du revenu permanent des pères.
Les résultats de l'analyse effectuée dans la présente étude indiquent que les études antérieures surestimaient l'ampleur de la mobilité intergénérationnelle des gains et du revenu au Canada. La nouvelle estimation de l'élasticité des gains de père en fils s'établit à environ 0,32, un résultat qui est sensiblement supérieur aux valeurs mentionnées dans les ouvrages publiés antérieurement (qui s'établissaient autour de 0,2). L'omission du biais lié au cycle de vie explique environ les deux tiers de la différence entre la dernière estimation et les précédentes, alors que le biais lié aux erreurs dans les variables rend compte du dernier tiers. Fait intéressant, l'analyse effectuée dans le cadre de la présente étude montre aussi que l'élasticité de père en fille est beaucoup moins sensible à ces biais. Enfin, l'étude révèle que l'incidence de ces biais est plus prononcée au sommet de la répartition du revenu et montre une tendance claire de non-linéarité dans la transmission intergénérationnelle des gains et du revenu au Canada. Plus particulièrement, le chemin pour atteindre le sommet de la répartition semble assez difficile pour les fils de pères à faible revenu. En revanche, ces mêmes fils semblent avoir une forte probabilité d'atteindre la classe moyenne.
Le reste de l'article est présenté comme suit. La section 2 décrit les données et le calcul des gains et du revenu permanents. La section 3 examine les sources de biais découlant des mesures imparfaites du revenu à vie et la façon dont ces biais peuvent influer sur les estimations de l'EIR. La section 4 présente les nouvelles estimations de la mobilité intergénérationnelle des gains et du revenu au Canada pour les paires père-fils et père-fille. La section 5 traite de la question de la non-linéarité et la section 6 présente les conclusions de l'étude.
2 Données et calcul du revenu à vie
L'analyse empirique réalisée dans le cadre de l'étude est fondée sur les dossiers fiscaux couplés des parents et de leurs descendants provenant d'une version actualisée de la base de données sur la mobilité intergénérationnelle du revenu (base de DMIR). Corak et Heisz (1999) présentent une description détaillée de la base de DMIR originale, qui couvrait la période de 1978 à 1995. Essentiellement, la base de DMIR est composée de trois sous-échantillons d'enfants âgés de 16 à 19 ans — en i) 1982, ii) 1984 et iii) 1986 — dont les dossiers fiscaux ont été couplés à ceux de leurs parents à partir des numéros d'assurance sociale des parents et des enfants et des données du fichier sur la famille T1 (FFT1) de Statistique Canada. Pour améliorer la couverture, les paires enfant-parent sont tirées du fichier FFT1 pour toutes les années de la période allant de 1982 à 1986. Lorsque des paires sont repérées pour plusieurs années, on conserve les plus anciennes. Une fois le lien enfant-parent établi, il est possible de retracer les gains annuels des enfants et des parents à partir de 1978 jusqu'à la dernière année pour laquelle des données sont disponibles (1995 dans la base de DMIR originale et 2008 dans la version actualisée) grâce aux fichiers d'impôt annuels (T1) et aux identificateurs longitudinaux uniques des participants fondés sur le numéro d'assurance sociale.
Le nombre d'années relativement faible pendant lesquelles les fils et les filles pouvaient être observés à l'âge adulte constitue l'une des limites de la version originale de la base de DMIR. Par exemple, même la cohorte d'enfants la plus âgée (celle des enfants nés entre 1963 et 1966) ne pouvait être observée que jusqu'à l'âge de 29 à 32 ans (en 1995). Les observations portant sur les deux autres cohortes d'enfants étaient limitées à des âges encore moins avancés. La version récemment mise à jour de la base de DMIR a la même structure que l'originale et porte sur les trois mêmes cohortes d'enfants, mais la période d'échantillonnage s'étend jusqu'en 2008. On peut donc maintenant observer les enfants de la cohorte de 1963 à 1966 jusqu'à l'âge de 42 à 45 ans et ceux des cohortes de 1965 à 1968 et de 1967 à 1970 jusqu'aux âges de 40 à 43 ans et de 38 à 41 ans, respectivement. La présente analyse est axée principalement sur la cohorte des enfants nés entre 1963 et 1966 et leurs pères.
Il importe de souligner qu'il n'a pas été possible de distinguer toutes les paires père-enfant dans la base de DMIR. Tout d'abord, un lien générationnel ne peut pas être établi si l'enfant vivant avec ses parents n'a pas produit de déclaration de revenus de 1982 à 1986. Il n'est pas possible non plus d'établir un lien générationnel pour les enfants de familles pour lesquelles on ne dispose pas de données sur le père pour la période allant de 1982 à 1986. Enfin, on n'a pas pu établir de lien père-enfant pour les enfants dont les dossiers n'ont pu être liés à aucune familleNote 3. Tout comme dans les études de Solon (1992) et de Corak et Heisz (1999), la présente analyse ne porte que sur l'aîné ou l'aînée lorsque plusieurs fils ou filles sont appariés au même père.
L'analyse examine trois mesures du revenu différentes : les gains, le revenu du marché et le revenu total. Les gains correspondent à la somme de la rémunération salariale figurant sur les feuillets T4 produits par les employeurs et des autres revenus d'emploi, y compris les pourboires, les gratifications et les allocations de présence. Le revenu du marché comprend en plus les revenus locatifs, les revenus d'un travail indépendant ainsi que les revenus tirés d'actifsNote 4. Le revenu total s'entend de la somme du revenu du marché et des transferts gouvernementaux, comme les prestations d'assurance-emploi et les prestations de retraite, à l'exclusion des impôtsNote 5. Tous les montants sont exprimés en dollars constants de 2010.
2.1 Une mesure améliorée des gains à vie et du revenu des pères
Il est bien connu, dans les ouvrages publiés, que l'utilisation du revenu annuel courant ou d'une seule année de revenu comme mesure indirecte du revenu permanent peut entraîner d'importants biais liés aux erreurs dans les variables dans l'estimation de l'EIR (Solon, 1999). L'une des solutions courantes consiste à utiliser des moyennes pluriannuelles pour réduire la composante transitoire du revenu. Toutefois, en l'absence d'un historique complet des données recueillies pendant toute la vie, le nombre d'années pour lesquelles les chercheurs peuvent observer le revenu est assez limité (généralement entre trois et cinq ans). Bien qu'il semble se dégager un consensus selon lequel des moyennes pluriannuelles constituent de meilleures mesures du revenu permanent que des données portant sur une seule année, il est peu question du nombre exact d'années nécessaires pour le calcul des moyennes. Une moyenne sur cinq ans est-elle suffisante pour obtenir une mesure indirecte du revenu à vie? À partir d'un ensemble unique (mais assez petit) de données d'enquête et de données administratives couplées, Mazumder (2005) conclut que des mesures indirectes sur une courte période du revenu permanent des pères sont quand même susceptibles d'introduire un biais, car la variance de la composante transitoire change considérablement en fonction de l'âge.
En outre, l'âge auquel la moyenne du revenu du père est calculée est souvent négligé dans les études publiées. Corak et Heisz (1999), par exemple, ont calculé le revenu permanent des pères en établissant la moyenne de leur revenu annuel pendant la période allant de 1978 à 1982. Toutefois, il est possible que certains pères de l'échantillon aient été trop jeunes ou trop vieux pendant la période observée et que, par conséquent, la moyenne ne représente pas correctement leur revenu permanent. Le tableau 1 en annexe donne la répartition selon l'âge des pères de la base de DMIR. De fait, près du quart des pères de l'échantillon pourraient être considérés comme étant trop jeunes ou trop vieux pendant la période de 1978 à 1982 : environ 5,3 % des pères avaient moins de 34 ans au début de 1978 et près de 18 % avaient 56 ans ou plus à la fin de 1982. Comme on pouvait s'y attendre, les gains de ces pères étaient sensiblement inférieurs à ceux de leurs contreparties dans la force de l'âge actif. Même dans ce dernier groupe, on constate une certaine variation : les gains moyens tendent à être plus élevés chez les pères de 41 à 45 ans pendant la période de 1978 à 1982.
Pour améliorer la mesure du revenu à vie des pères, on a calculé la moyenne de leur revenu annuel entre 35 et 55 ans, à condition que ce revenu ait été positif (500 $ et plus en dollars constants de 2010) pour au moins 10 de ces 21 années. La restriction relative à l'âge permet de s'assurer que les moyennes des revenus des pères de l'échantillon sont calculées à une étape comparable du cycle de vie et qu'elles sont donc moins influencées par les composantes transitoires généralement plus importantes en début et en fin de vie active. En restreignant l'échantillon aux pères ayant 10 années (non consécutives) ou plus de revenus positifs, on réduit davantage la variation introduite par quelques années à revenu élevé ou faible à l'âge où les pères sont les plus actifs. Soulignons que pour chaque père de la base de DMIR, les données sur les gains et le revenu étaient disponibles pour la période allant de 1978 à 1999. Cela signifie que pour les différentes cohortes de pères, la moyenne des gains peut être calculée à différentes années (voir le tableau 2 en annexe)Note 6. En raison du critère d'au moins 10 années de gains positifs et des restrictions relatives à l'âge (35 à 55 ans) et à la période (1978 à 1999), seuls les pères nés entre 1932 et 1955 pouvaient être inclus dans l'échantillonNote 7. Il importe de souligner que la mesure proposée est considérée comme une mesure indirecte améliorée du revenu à vie, plutôt qu'une mesure réelle du revenu. L'échantillon final comportait 356 321 pères (ayant des gains à vie positifs) qui pouvaient être appariés à un enfantNote 8. De ces pères, 56,4 % appartenaient à la cohorte de 1932 à 1938 et 40,2 %, à la cohorte de 1939 à 1945. Seulement 3,4 % étaient nés au cours de la période de 1946 à 1955.
3 Évaluation empirique du biais lié au cycle de vie et du biais lié aux erreurs dans les variables
À l'aide de données des États-Unis, Haider et Solon (2006) ont montré qu'il est possible de réduire considérablement le biais découlant de la variation liée au cycle de vie si l'on mesure les gains des enfants à la mi-carrière. Toutefois, la détermination de l'âge qui permet de réduire le biais lié au cycle de vie est une tâche empirique. Il importe de souligner qu'aux fins de la présente analyse, cet âge peut être propre à chaque pays. Dans la section qui suit, on applique le modèle généralisé des erreurs dans les variables de Haider et Solon aux données de la base de données sur la mobilité intergénérationnelle du revenu (base de DMIR), bien que le but de l'exercice ne soit pas d'examiner formellement le lien entre les gains annuels et les gains à vie, comme l'ont fait Haider et Solon (2006), puisqu'un tel examen exige des données historiques sur toute la durée de vie qui n'existent pas dans la base de DMIRNote 9. En outre, la présente analyse reposait sur un échantillon d'hommes liés de façon intergénérationnelle à un certain point de leur vie, qui ne peut être comparé aux échantillons plus vastes utilisés dans les études axées principalement sur la variation des gains au cours du cycle de vie. En conséquence, la section qui suit ne vise qu'à illustrer le biais des estimations de l'EIR, lorsque les gains à vie des pères et des enfants ne peuvent pas être mesurés avec exactitude.
Selon les conventions des ouvrages publiés sur la question, on peut décrire la relation entre les revenus des pères et ceux des fils à l'aide d'un modèle simple s'écrivant comme suit :
où est le logarithme du revenu à vie de l'enfant (ou du père), est une erreur aléatoire non corrélée avec , et correspond à l'EIR. Comme on ne connaît généralement pas le revenu permanent ni des pères ni des fils, toute tentative de mesure de cette variable à l'aide de données annuelles ou même de moyennes pluriannuelles (des méthodes courantes dans les études publiées) peut donner lieu à des estimations biaisées de l'EIR en raison des erreurs de mesure qui peuvent se produire dans les deux membres de l'équation. Pour tenir compte de ce fait, la présente analyse est faite selon le modèle de Haider et Solon (2006) et définit le premier membre de l'équation (gains des enfants, dans le cas présent) comme suit :
où correspond au revenu à vie calculé par approximation de (gains annuels à l'âge ), est un terme de perturbation aléatoire non corrélé avec et et est le coefficient de pente de la régression dite « ascendante » de sur . Supposons que l'on veuille estimer (1). En substituant (2) dans (1), on obtient
Par conséquent, (plutôt que ) correspond à la limite de probabilité du coefficient estimé sur . L'estimateur des moindres carrés ordinaires (MCO) de (1) est donc convergent uniquement lorsque . Un biais lié au cycle de vie se produit donc lorsque , et ce résultat peut varier en fonction de l'âge auquel les revenus sont observés. Haider et Solon (2006) en ont fait la démonstration pour les États-Unis. Les profils de varient sensiblement tout au long du cycle de vie : le profil commence à 0,24 à 19 ans, augmente jusqu'à environ 1 à 32 ans, puis diminue vers la fin de la vie active.
Le graphique 1 illustre les estimations de à partir des données de la base de DMIR dont il est question plus haut. Ces estimations correspondent aux coefficients de pente dans la régression ascendante du logarithme des gains annuels à l'âge sur le logarithme des gains à vie (équation 2). Comme il est expliqué plus haut, les gains à vie sont établis en calculant la moyenne des gains de 35 à 55 ans (sous réserve de gains positifs pour au moins 10 années). Cette mesure indirecte peut être considérée comme une estimation de la borne supérieure des gains à vie, puisqu'elle exclut les années de faibles gains (c.-à-d. le début et la fin du cycle de vie). Néanmoins, dans la mesure où les gains au plus fort de la vie active sont plus représentatifs des valeurs à vie (Haider et Solon, 2006; Böhlmark et Lindquist, 2006), les coefficients des régressions ascendantes peuvent fournir une indication de l'existence d'un biais lié au cycle de vie dans les estimations antérieures de l'EIR au Canada. Les résultats illustrés au graphique 1 montrent que n'est pas égal à 1 pendant tout le cycle de vie. La valeur s'établit à 0,47 à 25 ans et augmente graduellement pour atteindre 1 au début de la quarantaine. Elle continue à augmenter, jusqu'à environ 1,14 à 52 ans, puis redescend à moins de 1 après 56 ans. Fait important à souligner, les résultats illustrés au graphique 1 montrent que les estimations de l'EIR pourraient être considérablement sous-évaluées lorsqu'on observe les gains des fils à un jeune âge. Ces résultats semblent justifier la réévaluation des estimations antérieures. Le graphique 1 indique aussi qu'il est possible d'atténuer le biais découlant de la variation liée au cycle de vie en mesurant les gains des fils à la fin de la trentaine ou au début de la quarantaine (en tenant compte du fait que dans la présente analyse, la mesure du revenu permanent pourrait surestimer les gains à vie).

Tableau de données pour le graphique 1
| Âge | Régression ascendante du logarithme des gains annuels sur le logarithme des gains à vie | Intervalle de confiance à 95 % (limite inférieure) | Intervalle de confiance à 95 % (limite supérieure) |
|---|---|---|---|
| coefficient | |||
| 25 | 0,4733 | 0,3466 | 0,5999 |
| 26 | 0,4837 | 0,3932 | 0,5742 |
| 27 | 0,5491 | 0,4850 | 0,6131 |
| 28 | 0,6277 | 0,5807 | 0,6748 |
| 29 | 0,6231 | 0,5868 | 0,6595 |
| 30 | 0,6617 | 0,6346 | 0,6888 |
| 31 | 0,6755 | 0,6541 | 0,6969 |
| 32 | 0,7073 | 0,6911 | 0,7234 |
| 33 | 0,7390 | 0,7260 | 0,7520 |
| 34 | 0,7565 | 0,7462 | 0,7668 |
| 35 | 0,8215 | 0,8135 | 0,8294 |
| 36 | 0,8508 | 0,8443 | 0,8572 |
| 37 | 0,8697 | 0,8644 | 0,8749 |
| 38 | 0,8989 | 0,8943 | 0,9034 |
| 39 | 0,9161 | 0,9121 | 0,9201 |
| 40 | 0,9407 | 0,9372 | 0,9443 |
| 41 | 0,9617 | 0,9585 | 0,9650 |
| 42 | 0,9824 | 0,9794 | 0,9853 |
| 43 | 1,0028 | 1,0001 | 1,0055 |
| 44 | 1,0213 | 1,0188 | 1,0239 |
| 45 | 1,0354 | 1,0330 | 1,0379 |
| 46 | 1,0523 | 1,0499 | 1,0546 |
| 47 | 1,0730 | 1,0706 | 1,0753 |
| 48 | 1,0942 | 1,0918 | 1,0966 |
| 49 | 1,1134 | 1,1109 | 1,1159 |
| 50 | 1,1309 | 1,1283 | 1,1336 |
| 51 | 1,1385 | 1,1357 | 1,1413 |
| 52 | 1,1402 | 1,1372 | 1,1432 |
| 53 | 1,1338 | 1,1306 | 1,1371 |
| 54 | 1,1239 | 1,1202 | 1,1276 |
| 55 | 1,0920 | 1,0878 | 1,0963 |
| 56 | 0,9928 | 0,9875 | 0,9981 |
| 57 | 0,9334 | 0,9273 | 0,9395 |
| 58 | 0,8757 | 0,8688 | 0,8827 |
| 59 | 0,8202 | 0,8122 | 0,8283 |
| 60 | 0,7717 | 0,7622 | 0,7812 |
|
Notes : L'échantillon est composé de personnes ayant des gains à vie positifs. Pour chaque personne de l'échantillon, les gains à vie sont établis en calculant la moyenne des revenus de 35 à 55 ans, sous réserve d'un revenu positif de 500 $ et plus pour au moins 10 années. Tous les gains sont rajustés selon l'Indice des prix à la consommation en dollars constants de 2010. Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
|||
Haider et Solon (2006) ont aussi étudié l'erreur de mesure du second membre de l'équation. La variable explicative non observée (ici, les gains à vie du père) est calculée par approximation des gains annuels à l'âge , :
L'équation (4) correspond à ce qu'on appelle une « régression inverse » de sur , et la limite de probabilité du coefficient de pente estimé est
où
Quand , correspond simplement au biais d'atténuation classique. Toutefois, dépend aussi de la valeur de . Haider et Solon (2006) soutiennent que dans de rares cas, peut correspondre à un biais d'amplification, plutôt qu'à un biais d'atténuation.
On se sert de la mesure des gains à vie pour estimer les trajectoires de pour les Canadiens de sexe masculin (graphique 2). Comme on s'y attendait, l'utilisation des gains annuels dans le second membre de la régression pour produire des mesures indirectes des valeurs à vie entraîne un biais d'atténuation important (trait plein). Ce biais est particulièrement prononcé lorsque les gains courants sont observés au début ou à la fin du cycle de vie et demeure important (autour de 0,60) lorsque les gains sont mesurés aux années correspondant à la mi-carrière. Ces constatations vont dans le sens de celles de Björklund (1993) et de Böhlmark et Lindquist (2006) pour la Suède ainsi que de celles de Haider et Solon (2006) pour les États-Unis.
Dans la pratique, les chercheurs utilisent souvent des moyennes pluriannuelles plutôt que des gains annuels comme mesure indirecte des gains à vie. Dans quelle mesure une telle pratique réduit-elle le biais lié aux erreurs dans les variables? Pour répondre à cette question, on réévalue les régressions inverses en remplaçant les gains annuels courants par les gains annuels moyens sur une période de cinq ans, centrée à un âge particulierNote 10. Le graphique 2 (trait discontinu) révèle que le biais d'atténuation peut être réduit considérablement si, au lieu d'utiliser les gains annuels, on se sert des moyennes quinquennales pour produire une mesure indirecte des gains à vie. La valeur estimée de peut atteindre 0,85 lorsqu'on utilise les moyennes pluriannuelles des gains à mi-carrière. Le graphique 2 appuie en outre les résultats de Mazumder (2005), qui soutient que même des estimations fondées sur des moyennes quinquennales peuvent toujours être soumises à un biais non négligeable lié aux erreurs dans les variables. Dans l'ensemble, les résultats présentés aux graphiques 1 et 2 semblent indiquer que les études antérieures pourraient avoir sous-estimé l'EIR au Canada.

Tableau de données pour le graphique 2
| Âge | Régression inverse des gains à vie sur les gains annuels | Intervalles de confiance à 95 % (limite inférieure) | Intervalles de confiance à 95 % (limite supérieure) | Régression inverse des gains à vie sur les gains annuels « moyens » (moyenne sur ± 2 ans à chaque âge) |
|---|---|---|---|---|
| coefficient | ||||
| 25 | 0,2894 | 0,2120 | 0,3669 | 0,4913 |
| 26 | 0,3095 | 0,2516 | 0,3674 | 0,5948 |
| 27 | 0,3822 | 0,3377 | 0,4268 | 0,6611 |
| 28 | 0,4198 | 0,3884 | 0,4513 | 0,6695 |
| 29 | 0,4218 | 0,3972 | 0,4464 | 0,7253 |
| 30 | 0,4630 | 0,4440 | 0,4820 | 0,7411 |
| 31 | 0,4679 | 0,4531 | 0,4828 | 0,7631 |
| 32 | 0,5038 | 0,4923 | 0,5154 | 0,7735 |
| 33 | 0,5089 | 0,5000 | 0,5178 | 0,7879 |
| 34 | 0,5136 | 0,5065 | 0,5206 | 0,8104 |
| 35 | 0,5463 | 0,5410 | 0,5516 | 0,8268 |
| 36 | 0,5589 | 0,5546 | 0,5631 | 0,8337 |
| 37 | 0,5836 | 0,5801 | 0,5871 | 0,8493 |
| 38 | 0,5867 | 0,5837 | 0,5897 | 0,8523 |
| 39 | 0,5973 | 0,5947 | 0,5999 | 0,8545 |
| 40 | 0,6006 | 0,5984 | 0,6029 | 0,8571 |
| 41 | 0,6050 | 0,6029 | 0,6070 | 0,8586 |
| 42 | 0,6122 | 0,6103 | 0,6140 | 0,8562 |
| 43 | 0,6158 | 0,6141 | 0,6175 | 0,8570 |
| 44 | 0,6199 | 0,6184 | 0,6215 | 0,8563 |
| 45 | 0,6209 | 0,6195 | 0,6224 | 0,8537 |
| 46 | 0,6214 | 0,6200 | 0,6228 | 0,8502 |
| 47 | 0,6157 | 0,6143 | 0,6170 | 0,8411 |
| 48 | 0,6069 | 0,6056 | 0,6083 | 0,8281 |
| 49 | 0,5886 | 0,5873 | 0,5899 | 0,8111 |
| 50 | 0,5660 | 0,5647 | 0,5673 | 0,7900 |
| 51 | 0,5446 | 0,5433 | 0,5459 | 0,7670 |
| 52 | 0,5174 | 0,5160 | 0,5187 | 0,7398 |
| 53 | 0,4869 | 0,4855 | 0,4883 | 0,7069 |
| 54 | 0,4432 | 0,4418 | 0,4447 | 0,6680 |
| 55 | 0,3888 | 0,3873 | 0,3903 | 0,6227 |
| 56 | 0,3042 | 0,3026 | 0,3058 | 0,5704 |
| 57 | 0,2604 | 0,2587 | 0,2621 | 0,5073 |
| 58 | 0,2274 | 0,2256 | 0,2292 | 0,4339 |
| 59 | 0,1967 | 0,1948 | 0,1987 | Note ...: n'ayant pas lieu de figurer |
| 60 | 0,1662 | 0,1642 | 0,1683 | Note ...: n'ayant pas lieu de figurer |
|
... n'ayant pas lieu de figurer Notes : L'échantillon est composé de personnes ayant des gains à vie positifs. Pour chaque personne de l'échantillon, les gains à vie sont établis en calculant la moyenne des revenus de 35 à 55 ans, sous réserve d'un revenu positif de 500 $ et plus pour au moins 10 années. Tous les gains sont rajustés selon l'Indice des prix à la consommation en dollars constants de 2010. Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||||
3.1 Comparaison internationale des profils de biais
Dans la présente section, on compare les profils de biais du Canada à ceux d'autres pays. Cette comparaison pourrait permettre de mieux comprendre ce qui explique les différences entre les pays en ce qui concerne la transmission intergénérationnelle des gains. Quelques études portant sur l'association entre le revenu courant et le revenu à vie ont été réalisées. Haider et Solon (2006) ont été les premiers à proposer des estimations empiriques de et de fondées sur des données sur les gains couvrant presque toute la vie active des participants à un panel aux États-Unis. Deux autres études, à notre connaissance, reproduisent la méthode de Haider et Solon pour d'autres pays : celle de Böhlmark et Lindquist (2006) pour la Suède et celle de Brenner (2010) pour l'Allemagne, à partir des données de l'impôt de la Suède et du German Socio-Economic Panel, respectivementNote 11.
Les estimations de et obtenues dans le cadre de ces études sont présentées aux parties A et B du graphique 3 respectivement. Pour améliorer la comparabilité, les données sur les Canadiens sont limitées à celles des hommes nés durant la période allant de 1939 à 1945, une cohorte d'un groupe d'âge comparable à celui des cohortes de l'Allemagne et de la Suède, mais tout de même dix ans plus jeune que la cohorte des États-Unis. Le profil canadien porte sur une période plus courte, parce que la base de DMIR comprend des données sur les gains sur une période maximale de 21 ans. En règle générale, en ce qui concerne la valeur estimée de , les quatre études montrent que le scénario classique d'une valeur pendant tout le cycle de vie ne s'applique pas. En conséquence, l'utilisation des gains annuels du début de la vie active pour obtenir une mesure indirecte des gains à vie comme variable dépendante entraînerait un biais d'atténuation.
On constate aussi une similitude quant au moment (ou à l'âge) où le biais lié au cycle de vie est réduit. Pour les Canadiens, l'estimation de semble s'approcher de 1 à 40 ans, alors dans les trois autres pays, cela se produit plus tôt, soit vers la mi-trentaine. Ce résultat pourrait s'expliquer par le fait que la mesure des gains à vie au Canada dans la présente étude est surestimée par définition (parce que la moyenne des gains de chaque participant est calculée à un âge où il est le plus actif). Toutefois, les intervalles de confiance à 95 % associés à ces profils se chevauchent à la mi-carrière, soit de 40 à 41 ans. Après 41 ans, les profils de biais de chaque pays commencent à se différencier. Pour les États-Unis, les gains au cours de la vie sont sous-estimés à partir de la mi-carrière, alors que la situation semble être inversée pour l'Allemagne, où la valeur de continue de croître jusqu'à 44 ans et demeure au-dessus de 1 jusqu'à la fin de la vie active. Les profils du Canada et de la Suède se ressemblent un peu, en ce sens que dans les deux pays, la valeur estimée de atteint un sommet autour de 50 ans puis diminue par la suite, le recul étant plus prononcé pour les Canadiens (ce qui, encore une fois, pourrait s'expliquer par la mesure particulière utilisée ici).
Ces tendances permettent de mieux comprendre les comparaisons internationales de la transmission intergénérationnelle des gains. Tout d'abord, même lorsqu'on tient compte des différences dans la constitution de l'échantillon et dans la méthodologie, les estimations de l'EIR peuvent varier d'un pays à l'autre, en raison des différences dans l'âge auquel les gains des fils sont observés, toutes choses étant égales par ailleursNote 12. Par exemple, l'utilisation des gains des fils de la mi-quarantaine à la mi-cinquantaine tend à induire un biais d'atténuation pour les États-Unis, mais un biais d'amplification pour les trois autres pays. En revanche, le biais lié au cycle de vie semble être considérablement réduit pour tous les pays lorsque les gains des fils sont observés vers 40 ans.
En ce qui concerne la trajectoire de (partie B), tous les pays affichent un profil similaire en U inversé pendant le cycle de vie. L'utilisation des gains courants pour produire une mesure indirecte des gains à vie comme variable indépendante entraîne un biais vers le bas lorsqu'on utilise des gains du début et de la fin de la vie active. Dans tous les cas, le biais est plus petit à la mi-carrière, mais demeure bien en deçà de un. Cela semble indiquer qu'il n'est pas possible d'éliminer complètement le biais découlant de l'erreur de mesure dans le second membre de l'équation, quel que soit le stade de la vie active. Fait intéressant à souligner, comme la valeur de est d'environ 1 pour les quatre pays autour de 40 ans, correspond au biais d'atténuation attribuable à l'erreur de mesure classique. Encore une fois, les différences des valeurs de entre pays sont plus marquées au début et à la fin de la vie active.

Tableau de données pour le graphique 3
| Âge (à l'observation des gains) | Estimation de | Estimation de | ||||||
|---|---|---|---|---|---|---|---|---|
| Hommes canadiens 1939 à 1945 | Hommes américains 1931 à 1933 | Hommes allemands 1939 à 1944 | Hommes suédois 1939 à 1943 | Hommes canadiens 1939 à 1945 | Hommes américains 1931 à 1933 | Hommes allemands 1939 à 1944 | Hommes suédois 1939 à 1943 | |
| coefficient | ||||||||
| 20 | Note ...: n'ayant pas lieu de figurer | 0,251 | -0,055 | 0,020 | Note ...: n'ayant pas lieu de figurer | 0,199 | -0,016 | 0,020 |
| 21 | Note ...: n'ayant pas lieu de figurer | 0,171 | 0,013 | -0,050 | Note ...: n'ayant pas lieu de figurer | 0,094 | 0,003 | -0,010 |
| 22 | Note ...: n'ayant pas lieu de figurer | 0,284 | 0,139 | 0,160 | Note ...: n'ayant pas lieu de figurer | 0,144 | 0,038 | 0,050 |
| 23 | Note ...: n'ayant pas lieu de figurer | 0,317 | 0,215 | 0,165 | Note ...: n'ayant pas lieu de figurer | 0,258 | 0,087 | 0,050 |
| 24 | Note ...: n'ayant pas lieu de figurer | 0,405 | 0,278 | 0,280 | Note ...: n'ayant pas lieu de figurer | 0,352 | 0,106 | 0,090 |
| 25 | Note ...: n'ayant pas lieu de figurer | 0,432 | 0,400 | 0,370 | Note ...: n'ayant pas lieu de figurer | 0,652 | 0,211 | 0,110 |
| 26 | Note ...: n'ayant pas lieu de figurer | 0,541 | 0,457 | 0,560 | Note ...: n'ayant pas lieu de figurer | 0,620 | 0,282 | 0,325 |
| 27 | Note ...: n'ayant pas lieu de figurer | 0,508 | 0,537 | 0,670 | Note ...: n'ayant pas lieu de figurer | 0,696 | 0,359 | 0,455 |
| 28 | Note ...: n'ayant pas lieu de figurer | 0,643 | 0,643 | 0,720 | Note ...: n'ayant pas lieu de figurer | 0,684 | 0,371 | 0,410 |
| 29 | Note ...: n'ayant pas lieu de figurer | 0,760 | 0,683 | 0,780 | Note ...: n'ayant pas lieu de figurer | 0,629 | 0,412 | 0,437 |
| 30 | Note ...: n'ayant pas lieu de figurer | 0,835 | 0,738 | 0,810 | Note ...: n'ayant pas lieu de figurer | 0,630 | 0,460 | 0,370 |
| 31 | Note ...: n'ayant pas lieu de figurer | 0,945 | 0,817 | 0,880 | Note ...: n'ayant pas lieu de figurer | 0,644 | 0,472 | 0,400 |
| 32 | Note ...: n'ayant pas lieu de figurer | 0,993 | 0,883 | 0,840 | Note ...: n'ayant pas lieu de figurer | 0,625 | 0,496 | 0,490 |
| 33 | 0,6745 | 1,270 | 0,905 | 0,950 | 0,5209 | 0,527 | 0,487 | 0,490 |
| 34 | 0,6924 | 0,869 | 0,981 | 1,040 | 0,5389 | 0,756 | 0,512 | 0,440 |
| 35 | 0,7748 | 0,947 | 0,984 | 1,000 | 0,5558 | 0,700 | 0,576 | 0,500 |
| 36 | 0,8121 | 0,812 | 0,985 | 0,820 | 0,5694 | 0,803 | 0,567 | 0,550 |
| 37 | 0,8391 | 0,981 | 1,028 | 0,865 | 0,5909 | 0,688 | 0,580 | 0,600 |
| 38 | 0,8799 | 1,062 | 0,950 | 0,890 | 0,5834 | 0,640 | 0,632 | 0,508 |
| 39 | 0,9024 | 1,170 | 1,073 | 0,900 | 0,5943 | 0,573 | 0,588 | 0,504 |
| 40 | 0,9494 | 1,144 | 1,023 | 1,000 | 0,5891 | 0,578 | 0,649 | 0,500 |
| 41 | 0,9945 | 0,948 | 1,104 | 1,180 | 0,5837 | 0,630 | 0,585 | 0,385 |
| 42 | 1,0359 | 0,821 | 1,202 | 1,200 | 0,5833 | 0,700 | 0,561 | 0,425 |
| 43 | 1,0696 | 0,818 | 1,226 | 1,070 | 0,5800 | 0,663 | 0,570 | 0,500 |
| 44 | 1,0849 | 0,860 | 1,316 | 1,030 | 0,5812 | 0,667 | 0,531 | 0,580 |
| 45 | 1,0931 | 0,860 | 1,282 | 1,032 | 0,5827 | 0,642 | 0,557 | 0,482 |
| 46 | 1,1078 | 0,904 | 1,267 | 1,011 | 0,5834 | 0,568 | 0,578 | 0,565 |
| 47 | 1,1237 | 0,764 | 1,266 | 1,010 | 0,5680 | 0,628 | 0,569 | 0,410 |
| 48 | 1,1342 | 0,722 | 1,291 | 1,100 | 0,5489 | 0,594 | 0,578 | 0,480 |
| 49 | 1,1495 | 0,725 | 1,248 | 1,200 | 0,5281 | 0,584 | 0,602 | 0,385 |
| 50 | 1,1626 | 0,756 | 1,263 | 1,320 | 0,5043 | 0,519 | 0,552 | 0,350 |
| 51 | 1,1734 | 0,762 | 1,258 | 1,220 | 0,4792 | 0,512 | 0,569 | 0,360 |
| 52 | 1,1676 | 0,788 | 1,258 | 1,150 | 0,4416 | 0,484 | 0,554 | 0,412 |
| 53 | 1,1502 | 0,776 | 1,170 | 1,150 | 0,4133 | 0,477 | 0,561 | 0,460 |
| 54 | 1,1248 | 0,770 | 1,199 | 1,000 | 0,3776 | 0,456 | 0,519 | 0,365 |
| 55 | 1,0740 | 0,776 | 1,114 | 1,140 | 0,3309 | 0,429 | 0,481 | 0,495 |
| 56 | 0,9651 | 0,799 | 1,234 | 1,190 | 0,2597 | 0,423 | 0,471 | 0,475 |
| 57 | 0,8995 | 0,763 | 1,237 | 1,130 | 0,2229 | 0,379 | 0,440 | 0,460 |
| 58 | 0,8371 | 0,723 | 1,232 | 1,180 | 0,1963 | 0,368 | 0,380 | 0,460 |
| 59 | 0,7891 | 0,704 | 1,225 | 1,020 | 0,1754 | 0,315 | 0,354 | 0,510 |
| 60 | 0,7371 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 0,1521 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
|
... n'ayant pas lieu de figurer Sources : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu, pour les données du Canada; S. Haider et G. Solon, 2006, « Life-cycle Variation in the Association Between Current and Lifetime Earnings », pour les données des États-Unis; J. Brenner, 2010, « Life-cycle Variations in the Association Between Current and Lifetime Earnings: Evidence from German Natives and Guest Workers » pour les données de l'Allemagne; A. Böhlmark et M.J. Lindquist, 2006, « Life-cycle Variations in the Association Between Current and Lifetime Income: Replication and Extension for Sweden » pour les données de la Suède. |
||||||||
4 Nouvelles données concernant la mobilité intergénérationnelle des gains et du revenu au Canada
À quel point les estimations de l'élasticité intergénérationnelle au Canada sont-elles influencées par l'utilisation de mesures indirectes inexactes des gains à vie des pères et des fils? Pour répondre à cette question, deux scénarios faisant appel à des mesures différentes des gains à vie des pères sont présentés ci-dessous. Afin de permettre la comparaison des résultats avec ceux des études antérieures, le premier scénario reprend les paramètres de Corak et Heisz (1999) et définit les gains des pères comme la moyenne sur cinq ans pendant la période de 1978 à 1982.
Le trait plein du graphique 4 correspond aux estimations de l'EIR obtenues par une régression des MCO en vertu du scénario 1 pour différents âges d'observation des gains des fils. Dans l'ensemble, l'EIR estimée suit une trajectoire concave, ce qui reflète les différences au cours du cycle de vie dans l'ampleur du biais issu de l'erreur de mesure dans le premier membre de l'équation. Lorsque les gains des fils sont observés autour de 30 ans, comme l'on fait Corak et Heisz (1999), le modèle produit une estimation de (EIR) qui est presque identique à celle qu'ils ont obtenue, soit d'environ 0,227Note 13. L'élasticité estimée continue d'augmenter lorsqu'on mesure les gains des fils à des âges plus avancés. Elle atteint 0,29 lorsque les gains sont observés au début de la quarantaine (alors que la valeur de est proche de 1), ce qui indique un degré supérieur de persistance intergénérationnelle des gains.

Tableau de données pour le graphique 4
| Âge des fils | Scénario 1 : Moyenne de 1978 à 1982 (Corak et Heisz 1999) | Scénario 2 : Vie (moyenne de 35 à 55 ans) |
|---|---|---|
| coefficient | ||
| 20 | 0,016 | 0,042 |
| 21 | 0,008 | 0,042 |
| 22 | 0,036 | 0,071 |
| 23 | 0,040 | 0,080 |
| 24 | 0,083 | 0,126 |
| 25 | 0,129 | 0,172 |
| 26 | 0,164 | 0,208 |
| 27 | 0,188 | 0,232 |
| 28 | 0,204 | 0,251 |
| 29 | 0,218 | 0,258 |
| 30 | 0,226 | 0,272 |
| 31 | 0,236 | 0,284 |
| 32 | 0,248 | 0,292 |
| 33 | 0,258 | 0,298 |
| 34 | 0,268 | 0,309 |
| 35 | 0,273 | 0,311 |
| 36 | 0,277 | 0,319 |
| 37 | 0,281 | 0,319 |
| 38 | 0,281 | 0,312 |
| 39 | 0,284 | 0,318 |
| 40 | 0,286 | 0,321 |
| 41 | 0,290 | 0,322 |
| 42 | 0,291 | 0,322 |
| 43 | 0,292 | 0,320 |
| 44 | 0,292 | 0,316 |
| 45 | 0,286 | 0,323 |
|
Notes : Pour le scénario 1, les gains à vie sont établis en calculant la moyenne du revenu durant la période en années ou en âge indiquée, sous réserve d'un revenu positif de 500 $ et plus pour au moins trois années. Voir la note au bas du graphique 1. « EIR » est l'abréviation d'« élasticité intergénérationnelle du revenu ». M. Corak et A. Heisz, 1999, « The Integenerational Earnings and Income Mobility of Canadian Men: Evidence from Longitudinal Income Tax Data ». Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||
Outre le biais lié au cycle de vie, les estimations de l'EIR dépendent aussi de la façon dont les gains à vie des pères sont calculés. Dans le scénario 2, on utilise la mesure des gains à vie des pères proposée dans la présente analyse pour tenter de réduire l'erreur de mesure du second membre de l'équation. En règle générale, le scénario 2 (trait discontinu) produit une élasticité des gains supérieure à celle du premier scénario. La valeur estimée de s'accroît de trois points pour s'établir à 0,32 lorsqu'on observe les gains des fils à la mi-carrière. Le graphique 4 confirme que les erreurs de mesure des deux membres de l'équation peuvent entraîner un biais vers le bas dans les estimations de l'EIR. Plus particulièrement, le biais lié au cycle de vie du premier membre peut être important lorsque les EIR estimées sont fondées sur les gains des fils dès le début de leur vie active.
4.1 Les Canadiens sont-ils aussi mobiles qu'on le croyait?
Le tableau 1 présente de nouvelles estimations de l'EIR pour le Canada. On propose encore une fois différents scénarios pour mesurer les gains à vie des pères et des fils afin de mieux comprendre les incidences possibles des erreurs de mesure dans le premier et le second membre sur les coefficients estimés. Le scénario de base (scénario 1) repose sur une définition des gains à vie comparable à celle qu'ont utilisée Corak et Heisz (1999); le scénario 2 atténue le biais lié au cycle de vie du premier membre en observant les gains des fils à 40 ans; le scénario 3 réduit en plus le biais d'atténuation du second membre en utilisant la moyenne des gains des pères au plus fort de la vie active (de 35 à 55 ans); enfin, le dernier scénario (celui que l'on privilégie dans le contexte de la présente analyse) améliore la précision des gains à vie des fils grâce à des moyennes quinquennales à mi-carrière (c.-à-d. lorsque ceux-ci sont âgés de 38 à 42 ans). En plus des résultats pour les gains, les résultats pour le revenu du marché et le revenu total (avant impôts, après transferts) sont présentés.
En ce qui concerne les scénarios 3 et 4, l'élasticité intergénérationnelle des gains père-fils au Canada s'établit à environ 0,32, soit approximativement 46 % (ou 10 points) de plus que l'estimation généralement admise de 0,22 obtenue par Corak et Heisz (1999). Les deux sources de biais (cycle de vie et erreurs dans les variables) contribuent à la sous-évaluation des premières études. En règle générale, l'omission du biais lié au cycle de vie explique environ les deux tiers de l'écart entre l'estimation actuelle et la précédente, alors que le recours à une mesure indirecte moins exacte des gains à vie des pères rend compte du dernier tiers de l'écart. La comparaison des scénarios 3 et 4 au tableau 1 indique aussi que, lorsque les gains des fils sont observés au « bon » âge (c.-à-d. autour de la quarantaine), le fait de les remplacer par des moyennes quinquennales n'influe pas de façon importante sur l'estimation de l'EIR. Il pourrait donc être moins utile de produire une mesure indirecte des gains à vie des fils par des moyennes pluriannuelles si l'on peut observer les données sur les gains à la mi-carrière.
| Mesures indirectes | β (pères et fils) | |||||
|---|---|---|---|---|---|---|
| GainsTableau 1 - note 1 | Revenu du marchéTableau 1 - note 2 | Revenu totalTableau 1 - note 3 | ||||
| coefficient | erreur type | coefficient | erreur type | coefficient | erreur type | |
| Scénario 1 | ||||||
| Fils : à 30 ans Pères : moyenne de 1978 à 1982 |
0,227 | 0,003 | 0,230 | 0,003 | 0,222 | 0,002 |
| Scénario 2 | ||||||
| Fils : à 40 ans Pères : moyenne de 1978 à 1982 |
0,287 | 0,004 | 0,301 | 0,003 | 0,317 | 0,003 |
| Scénario 3 | ||||||
| Fils : à 40 ans Pères : moyenne de 35 à 55 ansTableau 1 - note 4 |
0,321 | 0,004 | 0,349 | 0,003 | 0,359 | 0,003 |
| Scénario 4 (modèle privilégié) | ||||||
| Fils : moyenne de 38 à 42 ansTableau 1 - note 5 Pères : moyenne de 35 à 55 ansTableau 1 - note 4 |
0,318 | 0,004 | 0,343 | 0,003 | 0,359 | 0,003 |
Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||||||
4.2 Mobilité du revenu du marché et du revenu total
En plus de contenir des données sur les gains, la base de données sur la mobilité intergénérationnelle du revenu (base de DMIR) comprend des données sur d'autres sources de revenus qui permettent aux chercheurs d'examiner la transmission intergénérationnelle du revenu du marché et du revenu total. Le fait de comprendre la mobilité du revenu peut améliorer la connaissance des mécanismes de transmission d'une génération à l'autre. Par exemple, des études antérieures ont permis d'établir des preuves manifestes d'une transmission intergénérationnelle des emplois (Kramarz et Skans, 2014), du travail indépendant (Lentz et Laband, 1990; Dunn et Holtz-Eakin, 2000; Sorensen, 2004), des postes de haut dirigeant (Pérez-González, 2006), des professions libérales (Aina et Nicoletti, 2013) et des rôles d'employeur (Corak et Piraino, 2011). Outre les transferts financiers, ces études font aussi ressortir l'importance d'autres mécanismes de transmission, comme la transmission du capital humain, des réseaux de contacts et, dans certains cas, du népotisme. Dunn et Holtz-Eakin (2000), par exemple, montrent que l'expérience de l'entrepreneuriat et le succès en affaires des parents ont une incidence importante sur la propension des enfants à devenir travailleurs indépendants.
Les études publiées indiquent que la persistance intergénérationnelle devrait être plus élevée pour le revenu du marché, puisque celui-ci comprend les revenus d'un travail indépendant et le revenu tiré d'actifs. Les résultats présentés au tableau 1 confirment cette hypothèse. L'échantillon examiné dans la présente analyse comprend en outre les paires père-fils ayant des revenus positifs d'un travail indépendant ou d'actifs. L'élasticité intergénérationnelle pour les pères et les fils affiche une autre hausse de 3 points, pour s'établir à environ 0,35 en vertu du modèle privilégié. Il importe aussi de souligner que les estimations fondées sur le scénario 1 sous-évaluent considérablement la dynamique du revenu du marché. Cela pourrait s'expliquer par le fait que les enfants travailleurs indépendants n'ont pas encore démarré — ou viennent juste de démarrer — leur entreprise lorsqu'ils sont au début de la trentaine. Il se pourrait aussi qu'en plus, le revenu d'actifs augmente plus rapidement au fil du temps pour les enfants de familles mieux nanties. En conséquence, le biais découlant de la variation liée au cycle de vie pourrait être plus prononcé pour le revenu du marché que pour les gains.
Lorsqu'on tient compte du revenu total, qui comprend aussi les transferts gouvernementaux (sauf les impôts), la mesure de l'importance de la transmission intergénérationnelle du bien-être économique au Canada se rapproche un peu plus de la réalité. Les personnes, pères et enfants, qui sont moins attachées au marché du travail sont maintenant comprises dans l'analyse, à condition qu'elles aient reçu des transferts gouvernementaux de n'importe quel ordre de gouvernement (c.-à-d. échelon local ou national). Les analyses publiées révèlent une forte corrélation intergénérationnelle pour les transferts d'aide gouvernementale (Corak, Gustaffsson et Österberg, 2004; Page, 2004). Si les enfants de pères à faible revenu sont plus susceptibles de recevoir de l'aide gouvernementale, cela pourrait se refléter dans les estimations de l'EIR. Toutefois, les résultats relatifs au revenu total présentés au tableau 1 indiquent que la persistance intergénérationnelle n'est que légèrement plus élevée, soit près de 0,36.
En résumé, les résultats présentés au tableau 1 montrent que le fait de mesurer les gains des pères et des fils de manière à réduire l'incidence des gains transitoires et le biais lié au cycle de vie mène à une EIR estimée d'environ 0,32 pour le Canada. L'élasticité est encore plus grande lorsqu'on tient compte du revenu du marché et du revenu total. Il importe de souligner que, bien que ce nouveau résultat placerait le Canada au milieu de la fourchette internationale des estimations de l'EIR (Björklund et Jäntti, 2010; Corak, 2013; Solon 2002), très peu de pays disposent de données permettant une analyse comparable à celle qui est faite ici. Les estimations qui ressemblent le plus aux coefficients de la présente étude sont probablement celles de Mazumder (2005). De fait, Mazumder a obtenu une EIR estimée d'un peu plus de 0,6 pour les États-Unis en appliquant à l'échantillon des restrictions comparables à celles qui sont utilisées ici. Comparativement à ces résultats, les estimations de la présente analyse confirment que le Canada demeure relativement plus mobile que les États-Unis. Toutefois, le « véritable » taux de transmission intergénérationnelle n'est peut-être pas aussi bas qu'on le pensait.
4.3 Différences entre les sexes en matière de mobilité intergénérationnelle du revenu
Le tableau 2 reprend les résultats de l'analyse en fonction des paires père-fille. En règle générale, la transmission intergénérationnelle des gains et du revenu est plus faible pour les filles que pour les fils. L'élasticité estimée est d'environ 0,23 pour les gains et va de 0,24 à 0,25 pour le revenu. Ces résultats semblent indiquer que la situation des filles dépend moins des gains et du revenu de leur père. Les résultats obtenus à partir du scénario de référence (scénario 1) se comparent à ceux des premières études canadiennes (Fortin et Lefebvre, 1998; Corak, 2001), qui ont également observé des élasticités intergénérationnelles des gains et du revenu pour les pères et les filles d'environ 0,2. Fait intéressant, contrairement à l'EIR père-fils, l'EIR père-fille ne semble pas être influencée par la variation liée au cycle de vie. En fait, les estimations fondées sur les gains des filles à 30 ans (scénario 1) ressemblent beaucoup à celles qui reposent sur les gains des filles à 40 ans (scénario 2).
Bien que cela puisse paraître curieux de prime abord, plusieurs facteurs peuvent expliquer ce résultat. En règle générale, les femmes sont plus susceptibles que les hommes d'interrompre leur carrière pour avoir des enfants et les élever au cours des premières années de leur vie active. Dans l'ensemble, les femmes sont moins attachées au marché du travail que les hommes. Ces constatations correspondent également aux résultats obtenus dans d'autres pays quant au rôle de l'« appariement assortatif », que les chercheurs ont désigné comme l'une des raisons possibles pour expliquer les EIR plus faibles pour les filles (voir Chadwick et Solon, 2002; Ermisch, Francesconi et Siedler, 2005; Raaum et coll., 2007). Lorsqu'il y a assortiment conjugal, les filles ayant un potentiel de gains supérieurs sont plus susceptibles d'épouser un homme ayant des gains élevés et pourraient choisir de travailler un moins grand nombre d'heures ou accepter une rémunération plus faible afin d'atteindre un meilleur équilibre entre la vie professionnelle et la vie familiale. Lorsqu'il y a appariement assortatif, les gains à vie du père pourraient être plus étroitement liés aux gains familiaux des filles (y compris ceux du conjoint) plutôt qu'à leurs propres gains.
Cela pourrait expliquer pourquoi l'EIR estimée pour les paires père-fille n'augmente pas autant que pour celles de type père-fils lorsque les gains sont mesurés dans la quarantaine. Bien que les estimations du scénario 1 puissent être soumises à un biais vers le bas en raison de la variation liée au cycle de vie, elles pourraient être moins touchées par l'appariement assortatif, puisque de nombreuses filles sont célibataires à 30 ans. En revanche, à 40 ans plusieurs filles sont mariées. En conséquence, les faibles coefficients estimés dans le scénario 2 semblent indiquer que l'appariement assortatif pourrait jouer un rôle dans la transmission intergénérationnelle du revenu de père en fille au Canada. Ils indiquent aussi que les futures études sur l'importance de la transmission intergénérationnelle du revenu pour les filles devraient tenir compte du revenu familial.
| Mesures indirectes | β (pères et filles) | |||||
|---|---|---|---|---|---|---|
| GainsTableau 2 - note 1 | Revenu du marchéTableau 2 - note 2 | Revenu totalTableau 2 - note 3 | ||||
| coefficient | erreur type | coefficient | erreur type | coefficient | erreur type | |
| Scénario 1 | ||||||
| Filles : à 30 ans Pères : moyenne de 1978 à 1982 |
0,191 | 0,004 | 0,212 | 0,003 | 0,213 | 0,003 |
| Scénario 2 | ||||||
| Filles : à 40 ans Pères : moyenne de 1978 à 1982 |
0,195 | 0,004 | 0,207 | 0,004 | 0,222 | 0,003 |
| Scénario 3 | ||||||
| Filles : à 40 ans Pères : moyenne de 35 à 55 ansTableau 2 - note 4 |
0,221 | 0,005 | 0,234 | 0,005 | 0,249 | 0,004 |
| Scénario 4 (modèle privilégié) | ||||||
| Filles : moyenne de 38 à 42 ansTableau 2 - note 5 Pères : moyenne de 35 à 55 ansTableau 2 - note 4 |
0,228 | 0,004 | 0,241 | 0,004 | 0,254 | 0,003 |
Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||||||
5 Non-linéarités
Les résultats de l'analyse de régression linéaire ci-dessus pourraient masquer des tendances non linéaires dans la transmission intergénérationnelle des gains. Diverses hypothèses ont été avancées pour expliquer les non-linéarités dans la relation entre les logarithmes des gains des pères et des fils. Par exemple, le modèle axé sur le capital humain proposé par Becker et Tomes (1986) suppose une courbe concave de la transmission intergénérationnelle des gains, les familles se trouvant au bas de la répartition des gains étant probablement plus susceptibles d'être soumises à des contraintes en matière d'emprunts. Les données empiriques relatives à cette hypothèse sont toutefois assez contradictoires. De fait, les études menées dans les pays de l'Europe du Nord révèlent plutôt une courbe convexe. Selon Bratsberg et coll. (2007), par exemple, la persistance intergénérationnelle des gains dans les pays nordiques est loin d'être linéaire, et une plus grande mobilité est observée dans les segments inférieurs de la distribution. De même, Björklund, Roine et Waldenström (2012) montrent une persistance intergénérationnelle très élevée des revenus des segments supérieurs en Suède, l'élasticité estimée s'établissant à environ 0,9, par rapport à une valeur moyenne de 0,26.
La section 5.1 présente des résultats relatifs à la non-linéarité de la persistance intergénérationnelle du revenu au Canada. L'analyse de la section précédente semble indiquer que les facteurs de transmission intergénérationnelle du revenu sont plus complexes pour les filles que pour les fils et pourraient exiger la prise en compte du revenu des conjoints. En conséquence, l'analyse ci-dessous ne porte que sur l'échantillon de paires père-fils. Comme la base de DMIR renferme des données sur près de 200 000 paires père-fils, il est possible d'examiner la non-linéarité éventuelle à un niveau plus détaillé que celui des études canadiennes précédentes.
5.1 Corrélation descriptive
On utilise une méthode descriptive et intuitive qui convient bien pour illustrer la relation entre les gains des pères et ceux des fils dans tous les segments de la répartition afin d'examiner la non-linéarité. Les pères sont répartis dans des centiles en fonction de leurs gains à vie. On obtient ainsi 100 points de données pour produire des diagrammes de dispersion. Pour chaque centile des gains des pères, le graphique 5 illustre le logarithme moyen des gains (partie A) et les parts des gains des fils et des pères (partie B). La courbe de la partie A montre clairement que la relation entre les gains des pères et les gains des fils au Canada n'est pas linéaire. Plus particulièrement, elle présente une forme quelque peu convexe. Le coefficient de pente estimé est de 0,36, mais la courbe est plate dans la partie inférieure de la répartition, augmente de façon monotone dans la partie centrale et s'accentue dans la partie supérieure. On peut tirer des renseignements intéressants de cette courbe. Tout d'abord, la mobilité des gains semble être plus élevée chez les enfants nés de pères appartenant aux 15 centiles inférieurs de la répartition des gains, puisque nombre d'entre eux se trouvent dans des centiles plus élevés que leur père. Ensuite, la persistance des gains tend à être très élevée chez les fils nés de pères appartenant aux 10 centiles supérieurs de la répartition des gains, ce qui donne à penser que la transmission intergénérationnelle des avantages est importante dans le haut de la répartition. Enfin, la persistance intergénérationnelle des gains est modérée entre le 15e et le 90e centile de la répartition des pères.
Les gains moyens d'un centile ne révèlent pas grand-chose à propos de la variation des gains à l'intérieur du centile. La partie B présente les parts des gains détenues par les fils et les pères dans chaque centile de la répartition des gains des pères. Si les gains à vie des fils dépendent de ceux du père, on pourrait s'attendre à ce que les parts des gains détenues par les fils dans chaque centile de la répartition des pères soient proches de 1 %. Inversement, une courbe s'approchant d'une ligne droite à 45 degrés indiquerait un degré élevé de persistance entre les gains des pères et ceux des fils. La partie B confirme généralement la non-linéarité de la transmission intergénérationnelle des gains dont il est question plus haut. Encore une fois, la mobilité semble être importante au bas de la répartition. Par exemple, la part des gains détenue par les pères du premier centile inférieur de la répartition n'est que de 0,1 %, alors que la part des gains des fils issus de ces familles s'élève à près de 0,8 % des gains totaux des fils. La corrélation est plus forte au milieu de la répartition, puisque les parts des gains des fils et des pères ont tendance à évoluer dans le même sens.
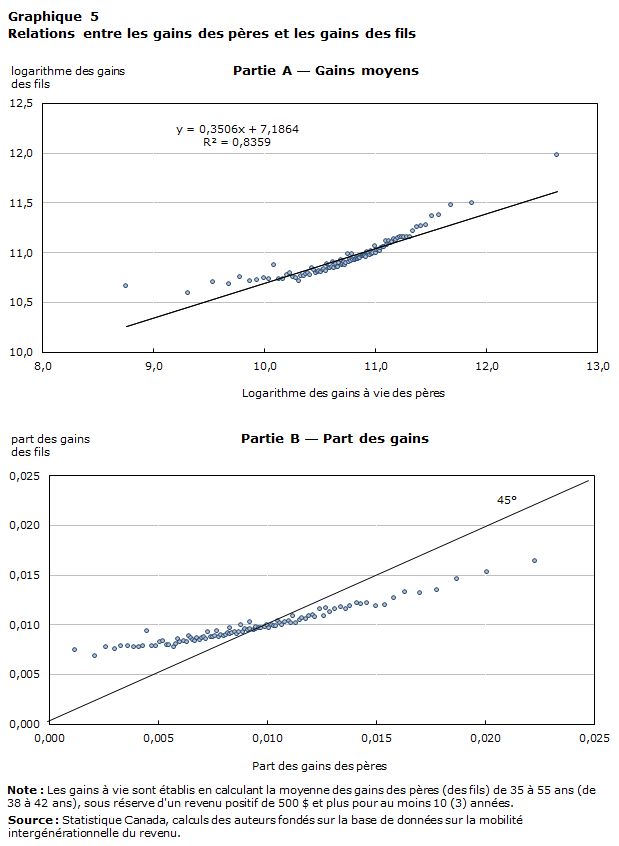
Tableau de données pour le graphique 5
| Centile de la distribution des gains des pères | Gains moyens | Part des gains | ||
|---|---|---|---|---|
| Pères | Fils | Pères | Fils | |
| logarithme | part | |||
| 1 | 8,757 | 10,663 | 0,0012 | 0,0074 |
| 2 | 9,315 | 10,593 | 0,0021 | 0,0068 |
| 3 | 9,537 | 10,699 | 0,0026 | 0,0077 |
| 4 | 9,681 | 10,685 | 0,0030 | 0,0075 |
| 5 | 9,785 | 10,753 | 0,0033 | 0,0078 |
| 6 | 9,867 | 10,707 | 0,0036 | 0,0078 |
| 7 | 9,934 | 10,724 | 0,0039 | 0,0077 |
| 8 | 9,994 | 10,740 | 0,0041 | 0,0077 |
| 9 | 10,046 | 10,735 | 0,0043 | 0,0078 |
| 10 | 10,090 | 10,868 | 0,0045 | 0,0093 |
| 11 | 10,131 | 10,732 | 0,0047 | 0,0078 |
| 12 | 10,168 | 10,734 | 0,0049 | 0,0078 |
| 13 | 10,201 | 10,775 | 0,0051 | 0,0082 |
| 14 | 10,232 | 10,787 | 0,0052 | 0,0083 |
| 15 | 10,260 | 10,746 | 0,0054 | 0,0079 |
| 16 | 10,286 | 10,741 | 0,0055 | 0,0079 |
| 17 | 10,310 | 10,711 | 0,0057 | 0,0077 |
| 18 | 10,334 | 10,761 | 0,0058 | 0,0080 |
| 19 | 10,356 | 10,760 | 0,0059 | 0,0085 |
| 20 | 10,376 | 10,783 | 0,0060 | 0,0082 |
| 21 | 10,396 | 10,788 | 0,0062 | 0,0083 |
| 22 | 10,414 | 10,767 | 0,0063 | 0,0082 |
| 23 | 10,431 | 10,837 | 0,0064 | 0,0088 |
| 24 | 10,448 | 10,825 | 0,0065 | 0,0086 |
| 25 | 10,465 | 10,790 | 0,0066 | 0,0084 |
| 26 | 10,480 | 10,803 | 0,0067 | 0,0083 |
| 27 | 10,496 | 10,816 | 0,0068 | 0,0086 |
| 28 | 10,511 | 10,806 | 0,0069 | 0,0084 |
| 29 | 10,525 | 10,821 | 0,0070 | 0,0086 |
| 30 | 10,540 | 10,835 | 0,0071 | 0,0087 |
| 31 | 10,554 | 10,807 | 0,0072 | 0,0085 |
| 32 | 10,567 | 10,882 | 0,0073 | 0,0092 |
| 33 | 10,581 | 10,840 | 0,0074 | 0,0087 |
| 34 | 10,593 | 10,842 | 0,0075 | 0,0087 |
| 35 | 10,606 | 10,855 | 0,0076 | 0,0088 |
| 36 | 10,618 | 10,901 | 0,0077 | 0,0093 |
| 37 | 10,630 | 10,840 | 0,0078 | 0,0087 |
| 38 | 10,642 | 10,878 | 0,0079 | 0,0089 |
| 39 | 10,654 | 10,852 | 0,0080 | 0,0088 |
| 40 | 10,666 | 10,854 | 0,0081 | 0,0089 |
| 41 | 10,677 | 10,888 | 0,0082 | 0,0091 |
| 42 | 10,688 | 10,925 | 0,0083 | 0,0096 |
| 43 | 10,698 | 10,870 | 0,0083 | 0,0090 |
| 44 | 10,709 | 10,880 | 0,0084 | 0,0091 |
| 45 | 10,719 | 10,900 | 0,0085 | 0,0092 |
| 46 | 10,730 | 10,874 | 0,0086 | 0,0090 |
| 47 | 10,740 | 10,890 | 0,0087 | 0,0092 |
| 48 | 10,751 | 10,978 | 0,0088 | 0,0099 |
| 49 | 10,761 | 10,903 | 0,0089 | 0,0092 |
| 50 | 10,771 | 10,934 | 0,0090 | 0,0095 |
| 51 | 10,782 | 10,910 | 0,0091 | 0,0094 |
| 52 | 10,792 | 10,980 | 0,0092 | 0,0102 |
| 53 | 10,803 | 10,925 | 0,0092 | 0,0095 |
| 54 | 10,813 | 10,918 | 0,0094 | 0,0094 |
| 55 | 10,823 | 10,933 | 0,0095 | 0,0095 |
| 56 | 10,834 | 10,945 | 0,0095 | 0,0097 |
| 57 | 10,844 | 10,933 | 0,0096 | 0,0096 |
| 58 | 10,855 | 10,937 | 0,0097 | 0,0096 |
| 59 | 10,865 | 10,944 | 0,0099 | 0,0097 |
| 60 | 10,876 | 10,963 | 0,0100 | 0,0099 |
| 61 | 10,886 | 10,966 | 0,0101 | 0,0096 |
| 62 | 10,897 | 10,958 | 0,0102 | 0,0099 |
| 63 | 10,907 | 10,962 | 0,0103 | 0,0098 |
| 64 | 10,918 | 10,954 | 0,0104 | 0,0098 |
| 65 | 10,929 | 11,001 | 0,0105 | 0,0103 |
| 66 | 10,939 | 10,991 | 0,0106 | 0,0101 |
| 67 | 10,950 | 10,969 | 0,0107 | 0,0099 |
| 68 | 10,961 | 11,015 | 0,0108 | 0,0102 |
| 69 | 10,972 | 10,977 | 0,0110 | 0,0103 |
| 70 | 10,983 | 10,993 | 0,0111 | 0,0101 |
| 71 | 10,994 | 11,058 | 0,0112 | 0,0108 |
| 72 | 11,006 | 10,997 | 0,0113 | 0,0101 |
| 73 | 11,018 | 11,020 | 0,0115 | 0,0104 |
| 74 | 11,030 | 11,024 | 0,0116 | 0,0106 |
| 75 | 11,042 | 11,017 | 0,0118 | 0,0105 |
| 76 | 11,054 | 11,044 | 0,0119 | 0,0108 |
| 77 | 11,067 | 11,054 | 0,0121 | 0,0109 |
| 78 | 11,081 | 11,057 | 0,0122 | 0,0107 |
| 79 | 11,094 | 11,112 | 0,0124 | 0,0115 |
| 80 | 11,108 | 11,070 | 0,0126 | 0,0108 |
| 81 | 11,123 | 11,116 | 0,0127 | 0,0116 |
| 82 | 11,138 | 11,091 | 0,0129 | 0,0112 |
| 83 | 11,153 | 11,106 | 0,0131 | 0,0115 |
| 84 | 11,169 | 11,130 | 0,0134 | 0,0117 |
| 85 | 11,186 | 11,124 | 0,0136 | 0,0115 |
| 86 | 11,203 | 11,147 | 0,0138 | 0,0118 |
| 87 | 11,221 | 11,157 | 0,0141 | 0,0121 |
| 88 | 11,241 | 11,151 | 0,0143 | 0,0120 |
| 89 | 11,262 | 11,148 | 0,0146 | 0,0121 |
| 90 | 11,285 | 11,156 | 0,0150 | 0,0118 |
| 91 | 11,311 | 11,153 | 0,0154 | 0,0119 |
| 92 | 11,339 | 11,212 | 0,0158 | 0,0126 |
| 93 | 11,371 | 11,254 | 0,0163 | 0,0132 |
| 94 | 11,410 | 11,260 | 0,0170 | 0,0131 |
| 95 | 11,455 | 11,273 | 0,0178 | 0,0134 |
| 96 | 11,508 | 11,365 | 0,0187 | 0,0146 |
| 97 | 11,578 | 11,377 | 0,0201 | 0,0153 |
| 98 | 11,682 | 11,472 | 0,0223 | 0,0164 |
| 99 | 11,868 | 11,490 | 0,0269 | 0,0166 |
| 100 | 12,634 | 11,979 | 0,0573 | 0,0280 |
|
Note : Les gains à vie sont établis en calculant la moyenne des gains des pères (des fils) de 35 à 55 ans (de 38 à 42 ans), sous réserve d'un revenu positif de 500 $ et plus pour au moins 10 (3) années. Pour la partie A : y = 0,3506x + 7,1864; R au carré = 0,8359. Une ligne de tendance apparaît aussi dans le graphique de la partie A. Le graphique de la partie B présente une ligne de 45 degrés dans la zone de traçage, qui débute à 0,000. Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||||
Les tendances de non-linéarité observées au graphique 5 ne semblent pas correspondre au modèle de contraintes d'emprunt de Becker et Tomes (1986) ou de Mulligan (1997), en vertu duquel on s'attend à une courbe concave de la relation entre les gains des enfants et ceux des parents. Selon les résultats de ces études, les parents de la moitié inférieure de la répartition sont plus susceptibles d'être soumis à des contraintes en matière de crédit. En vertu de certaines autres hypothèses, cela impliquerait des investissements sous-optimaux dans le capital humain des enfants se trouvant au bas de la répartition des gains des pères et donnerait donc une corrélation plus forte (c.-à-d. une courbe plus accentuée) entre les gains des pères et ceux des fils. On suppose que les contraintes d'emprunt diminuent graduellement dans les centiles supérieurs de la répartition; les gains des fils dépendraient donc moins de ceux des pères dans la moitié supérieure de la répartition.
La violation de certaines des hypothèses du modèle pourrait expliquer pourquoi on n'obtient pas la courbe concave attendue. Han et Mulligan (2001), par exemple, ont montré que l'hétérogénéité des perspectives innées de gains des enfants ainsi que de l'altruisme des parents rend difficile la vérification de l'existence de familles soumises à des contraintes en matière de crédit. La tendance à la non-linéarité observée dans les données canadiennes semble toutefois mieux correspondre aux résultats obtenus dans les pays nordiques, c'est-à-dire une courbe convexe de la relation intergénérationnelle des gains. Bratsberg et coll. (2007) soutiennent que des facteurs institutionnels pourraient expliquer pourquoi la mobilité est plus élevée au bas de la répartition. Ils avancent notamment que les systèmes d'éducation et de bien-être des pays nordiques facilitent la mobilité vers le haut des jeunes dont les parents disposent de peu de ressources. Fait intéressant à souligner, les constatations de la présente étude au Canada diffèrent des tendances estimées aux États-Unis, qui montrent une relation presque parfaitement linéaire entre les rangs des enfants et ceux des parents dans la répartition du revenu (Chetty et coll., 2014)Note 14.
En résumé, les tendances non linéaires illustrées dans le graphique 5 indiquent qu'un seul coefficient de l'EIR pourrait ne pas être suffisant pour brosser un tableau exact de la mobilité intergénérationnelle des gains au Canada. Corak et Heisz (1999) ont tiré une conclusion similaire en examinant la nature de ces non-linéarités à l'aide de matrices de transition du revenu et d'une technique non paramétrique. Ci-dessous, on utilise plutôt deux approches paramétriques différentes, c'est-à-dire une régression polynomiale de degré supérieur et une régression quantile, pour étudier les non-linéarités. Ces résultats paramétriques sont ensuite brièvement comparés aux constatations de Corak et Heisz (1999) dans la dernière section de l'article.
5.2 Régressions non linéaires : polynômes de degré supérieur
Comme l'ont montré Bratsberg et coll. (2007), on peut utiliser des formes fonctionnelles plus souples (c.-à-d. des polynômes de degré supérieur) pour estimer le modèle intergénérationnel des gains qui convient le mieux aux données. Dans la présente analyse, les coefficients d'un polynôme du quatrième degré sont estimés à partir des DIR et utilisés pour calculer l'EIR pour chaque centile de la répartition des gains des pères. Les résultats, présentés au graphique 6, confirment que le degré de mobilité intergénérationnelle des gains au Canada se caractérise par une courbe non linéaire marquée. En fait, le graphique 6 montre une trajectoire de croissance logarithmique. Plus particulièrement, l'élasticité est assez faible pour les fils appartenant aux deux centiles inférieurs de la répartition des gains des pères (environ 0,1); cela indique un degré important de mobilité vers le haut pour les fils nés d'un père à très faibles gains.
Plus loin dans la répartition des gains des pères, le degré de mobilité commence à diminuer. L'EIR estimée augmente rapidement pour atteindre 0,32 (la même valeur que le coefficient estimé à partir de la spécification linéaire) environ au 23e centile. Par la suite, la persistance des gains augmente de façon monotone avec les gains des pères. L'élasticité estimée plafonne à 0,45 au 98e centile et au 99e centile des gains des pères, ce qui semble indiquer une forte corrélation intergénérationnelle des gains dans les familles à gains très élevés.
Il ressort des données illustrées dans le graphique 6 une caractéristique importante : les estimations du modèle linéaire (0,32) semblent sous-évaluer la transmission intergénérationnelle des gains pour la majeure partie de la population. Ces résultats appuient les conclusions de Bratsberg et coll. (2007), qui soutiennent que des comparaisons transnationales de la mobilité intergénérationnelle des gains fondées sur des spécifications plus souples pourraient donner des résultats plus significatifs. De fait, la comparaison des résultats de la présente analyse avec ceux de Bratsberg et coll. donne à penser que la tendance de la mobilité intergénérationnelle des gains au Canada est très semblable à celle qu'on observe dans les pays scandinaves : une relation intergénérationnelle uniforme dans les segments inférieurs de la répartition des pères et une corrélation de plus en plus positive dans les segments intermédiaires et supérieurs. Fait intéressant, on n'observe pas cette tendance aux États-Unis ni au Royaume-Uni (Bratsberg et coll., 2007).
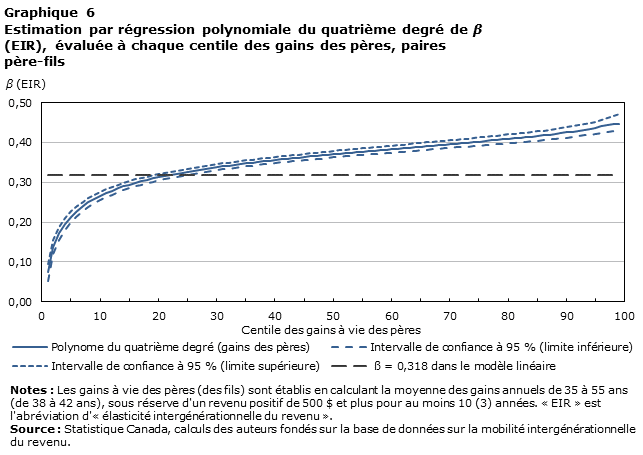
Tableau de données pour le graphique 6
| Centile des gains à vie des pères | Polynome du quatrième degré (gains des pères) | Intervalle de confiance à 95 % (limite inférieure) | Intervalle de confiance à 95 % (limite supérieure) | β = 0,318 dans le modèle linéaire |
|---|---|---|---|---|
| β (EIR) | ||||
| 0 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| 1 | 0,0743 | 0,0528 | 0,0958 | 0,318 |
| 2 | 0,1367 | 0,1189 | 0,1546 | 0,318 |
| 3 | 0,1719 | 0,1560 | 0,1879 | 0,318 |
| 4 | 0,1958 | 0,1812 | 0,2104 | 0,318 |
| 5 | 0,2134 | 0,1998 | 0,2270 | 0,318 |
| 6 | 0,2274 | 0,2146 | 0,2402 | 0,318 |
| 7 | 0,2394 | 0,2273 | 0,2514 | 0,318 |
| 8 | 0,2496 | 0,2382 | 0,2611 | 0,318 |
| 9 | 0,2584 | 0,2475 | 0,2694 | 0,318 |
| 10 | 0,2661 | 0,2556 | 0,2766 | 0,318 |
| 11 | 0,2731 | 0,2629 | 0,2832 | 0,318 |
| 12 | 0,2790 | 0,2693 | 0,2888 | 0,318 |
| 13 | 0,2846 | 0,2751 | 0,2940 | 0,318 |
| 14 | 0,2897 | 0,2805 | 0,2989 | 0,318 |
| 15 | 0,2942 | 0,2852 | 0,3032 | 0,318 |
| 16 | 0,2984 | 0,2896 | 0,3072 | 0,318 |
| 17 | 0,3025 | 0,2939 | 0,3110 | 0,318 |
| 18 | 0,3062 | 0,2978 | 0,3146 | 0,318 |
| 19 | 0,3098 | 0,3015 | 0,3180 | 0,318 |
| 20 | 0,3130 | 0,3049 | 0,3212 | 0,318 |
| 21 | 0,3161 | 0,3081 | 0,3241 | 0,318 |
| 22 | 0,3189 | 0,3109 | 0,3268 | 0,318 |
| 23 | 0,3217 | 0,3138 | 0,3295 | 0,318 |
| 24 | 0,3243 | 0,3165 | 0,3321 | 0,318 |
| 25 | 0,3268 | 0,3191 | 0,3345 | 0,318 |
| 26 | 0,3293 | 0,3216 | 0,3369 | 0,318 |
| 27 | 0,3316 | 0,3240 | 0,3392 | 0,318 |
| 28 | 0,3338 | 0,3262 | 0,3414 | 0,318 |
| 29 | 0,3360 | 0,3285 | 0,3436 | 0,318 |
| 30 | 0,3381 | 0,3306 | 0,3457 | 0,318 |
| 31 | 0,3402 | 0,3327 | 0,3477 | 0,318 |
| 32 | 0,3422 | 0,3347 | 0,3497 | 0,318 |
| 33 | 0,3441 | 0,3366 | 0,3516 | 0,318 |
| 34 | 0,3460 | 0,3385 | 0,3535 | 0,318 |
| 35 | 0,3478 | 0,3403 | 0,3553 | 0,318 |
| 36 | 0,3496 | 0,3421 | 0,3571 | 0,318 |
| 37 | 0,3512 | 0,3437 | 0,3588 | 0,318 |
| 38 | 0,3529 | 0,3454 | 0,3605 | 0,318 |
| 39 | 0,3546 | 0,3470 | 0,3622 | 0,318 |
| 40 | 0,3562 | 0,3486 | 0,3638 | 0,318 |
| 41 | 0,3578 | 0,3501 | 0,3654 | 0,318 |
| 42 | 0,3592 | 0,3516 | 0,3669 | 0,318 |
| 43 | 0,3607 | 0,3530 | 0,3684 | 0,318 |
| 44 | 0,3622 | 0,3544 | 0,3699 | 0,318 |
| 45 | 0,3636 | 0,3558 | 0,3714 | 0,318 |
| 46 | 0,3650 | 0,3572 | 0,3728 | 0,318 |
| 47 | 0,3664 | 0,3585 | 0,3743 | 0,318 |
| 48 | 0,3678 | 0,3598 | 0,3757 | 0,318 |
| 49 | 0,3691 | 0,3611 | 0,3771 | 0,318 |
| 50 | 0,3705 | 0,3624 | 0,3785 | 0,318 |
| 51 | 0,3719 | 0,3638 | 0,3800 | 0,318 |
| 52 | 0,3732 | 0,3650 | 0,3813 | 0,318 |
| 53 | 0,3745 | 0,3663 | 0,3827 | 0,318 |
| 54 | 0,3758 | 0,3675 | 0,3841 | 0,318 |
| 55 | 0,3771 | 0,3688 | 0,3855 | 0,318 |
| 56 | 0,3784 | 0,3700 | 0,3869 | 0,318 |
| 57 | 0,3797 | 0,3712 | 0,3882 | 0,318 |
| 58 | 0,3810 | 0,3724 | 0,3896 | 0,318 |
| 59 | 0,3823 | 0,3737 | 0,3910 | 0,318 |
| 60 | 0,3836 | 0,3748 | 0,3923 | 0,318 |
| 61 | 0,3849 | 0,3761 | 0,3937 | 0,318 |
| 62 | 0,3861 | 0,3772 | 0,3950 | 0,318 |
| 63 | 0,3874 | 0,3784 | 0,3963 | 0,318 |
| 64 | 0,3886 | 0,3796 | 0,3977 | 0,318 |
| 65 | 0,3899 | 0,3807 | 0,3990 | 0,318 |
| 66 | 0,3911 | 0,3819 | 0,4004 | 0,318 |
| 67 | 0,3923 | 0,3830 | 0,4017 | 0,318 |
| 68 | 0,3936 | 0,3841 | 0,4030 | 0,318 |
| 69 | 0,3948 | 0,3853 | 0,4043 | 0,318 |
| 70 | 0,3961 | 0,3864 | 0,4057 | 0,318 |
| 71 | 0,3973 | 0,3875 | 0,4071 | 0,318 |
| 72 | 0,3986 | 0,3887 | 0,4084 | 0,318 |
| 73 | 0,3999 | 0,3899 | 0,4098 | 0,318 |
| 74 | 0,4012 | 0,3911 | 0,4113 | 0,318 |
| 75 | 0,4025 | 0,3923 | 0,4127 | 0,318 |
| 76 | 0,4038 | 0,3934 | 0,4141 | 0,318 |
| 77 | 0,4051 | 0,3947 | 0,4156 | 0,318 |
| 78 | 0,4065 | 0,3959 | 0,4171 | 0,318 |
| 79 | 0,4079 | 0,3971 | 0,4186 | 0,318 |
| 80 | 0,4093 | 0,3984 | 0,4202 | 0,318 |
| 81 | 0,4107 | 0,3997 | 0,4218 | 0,318 |
| 82 | 0,4122 | 0,4009 | 0,4234 | 0,318 |
| 83 | 0,4136 | 0,4022 | 0,4250 | 0,318 |
| 84 | 0,4151 | 0,4036 | 0,4267 | 0,318 |
| 85 | 0,4166 | 0,4049 | 0,4284 | 0,318 |
| 86 | 0,4181 | 0,4062 | 0,4301 | 0,318 |
| 87 | 0,4198 | 0,4076 | 0,4319 | 0,318 |
| 88 | 0,4215 | 0,4091 | 0,4339 | 0,318 |
| 89 | 0,4233 | 0,4106 | 0,4359 | 0,318 |
| 90 | 0,4252 | 0,4123 | 0,4382 | 0,318 |
| 91 | 0,4273 | 0,4140 | 0,4405 | 0,318 |
| 92 | 0,4294 | 0,4158 | 0,4430 | 0,318 |
| 93 | 0,4318 | 0,4177 | 0,4458 | 0,318 |
| 94 | 0,4344 | 0,4198 | 0,4490 | 0,318 |
| 95 | 0,4373 | 0,4220 | 0,4525 | 0,318 |
| 96 | 0,4403 | 0,4243 | 0,4564 | 0,318 |
| 97 | 0,4438 | 0,4265 | 0,4611 | 0,318 |
| 98 | 0,4475 | 0,4280 | 0,4670 | 0,318 |
| 99 | 0,4475 | 0,4222 | 0,4729 | 0,318 |
| 100 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
|
... n'ayant pas lieu de figurer Notes : Les gains à vie des pères (des fils) sont établis en calculant la moyenne des gains annuels de 35 à 55 ans (de 38 à 42 ans), sous réserve d'un revenu positif de 500 $ et plus pour au moins 10 (3) années. « EIR » est l'abréviation d'« élasticité intergénérationnelle du revenu ». Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||||
5.3 Régressions quantiles
Bien que les résultats présentés ci-dessus indiquent une EIR non linéaire dans toute la répartition des gains des pères, il est intéressant de déterminer si la mobilité est différente dans la répartition des gains des fils. Comme l'ont souligné Mulligan (1997) et Corak et Heisz (1999), le montant optimal de l'investissement dans le capital humain réalisé par les pères peut aussi dépendre — de façon positive — des aptitudes de l'enfant. Ces auteurs soulignent que les parents les plus susceptibles d'être soumis à des contraintes en matière de crédit sont les parents à faible revenu ayant des enfants qui ont de grandes aptitudes. Cela soulève la question de la façon dont se comparent les gains des enfants ayant de grandes aptitudes provenant d'un milieu à faible revenu par rapport à ceux de leurs contreparties de familles à revenu élevé. La réponse à cette question pourrait éclairer les discussions stratégiques relatives à l'égalité des chances au Canada. Cette notion se rapporte à l'existence d'occasions économiques similaires pour les enfants ayant des aptitudes comparables, quel que soit leur milieu d'origine (Roemer, 1998).
Grawe (2004) propose d'utiliser des régressions quantiles pour examiner ce genre de question. Par exemple, l'élasticité élevée des centiles supérieurs de la répartition des gains des enfants pourrait indiquer que les enfants ayant des gains élevés viennent presque exclusivement de familles dont le père avait des gains élevés. À moins de formuler des hypothèses particulières quant au caractère héréditaire des aptitudes innées, cela peut être interprété comme une preuve d'inégalité des chances, c'est-à-dire que les enfants ayant de grandes aptitudes provenant d'un milieu à faibles gains ont peu de chance d'atteindre leur plein potentiel et d'avoir un revenu élevé une fois adultes.
Le graphique 7 présente les estimations par régression quantile pour les paires père-fils de l'échantillon de la présente étude, selon la méthode de Grawe (2004). Les estimations sont produites pour chaque centile (du 1er au 99e) des gains des fils. Les intervalles de confiance à 95 % estimés sont aussi indiqués. Les résultats des régressions quantiles montrent clairement une tendance de non-linéarité dans la répartition des gains des fils. L'élasticité des gains estimés est relativement faible (environ 0,2) dans les deux centiles inférieurs de la répartition des gains des fils, puis monte à 0,35 au 10e centile et demeure stable à environ 0,33 à 0,34 dans la moitié inférieure de la répartition. Elle diminue ensuite graduellement pour atteindre 0,27 du 80e au 85e centile, puis monte de nouveau à 0,41 au 99e centile.
Trois profils distincts de transmission intergénérationnelle des gains se dégagent de l'analyse de régression quantile. Premièrement, les coefficients de régression quantile sont assez faibles pour les fils des deux centiles inférieurs de la répartition, c'est-à-dire qu'une grande proportion des fils ayant les gains les plus faibles n'ont pas un père se trouvant lui aussi tout au bas de la répartition des gains de sa génération. Cela signifie que les fils de pères des segments de gains les plus bas sont relativement mobiles, ce qui correspond aux résultats obtenus plus haut à l'aide du modèle polynomial. Deuxièmement, du 10e au 85e centile de la répartition des gains des fils, la persistance est assez élevée au début (l'élasticité estimée est supérieure à 0,35 au 10e centile), diminue lentement dans la moitié inférieure, puis recule plus abruptement dans la moitié intermédiaire supérieure. Une élasticité plutôt élevée dans les segments intermédiaires inférieurs de la répartition des fils indique qu'une fraction considérable de fils ayant des gains intermédiaires ont un père se trouvant dans une situation économique similaire. Cette corrélation devient toutefois moins claire à mesure que les gains des fils augmentent. La mobilité des gains commence à augmenter pour les fils des segments intermédiaires supérieurs de la répartition. L'élasticité estimée diminue, passant de 0,33 à la médiane à 0,27 au 85e centile. Cela indique que les fils provenant d'un grand éventail de milieux pour ce qui est des gains ont de bonnes chances d'avoir des gains supérieurs à la moyenne une fois adultes. Troisièmement, le graphique 7 montre l'inverse des coefficients de régression quantile dans les centiles supérieurs (85e à 99e centile), ce qui révèle un degré accru de persistance des gains pour les fils ayant des gains élevés. Les coefficients estimés s'établissent à 0,38 et à 0,41 pour les deux centiles supérieurs, respectivement, ce qui signifie qu'une fraction importante de ceux qui se taillent une place dans les groupes de gains supérieurs ont un père ayant aussi des gains élevés.
Finalement, le graphique 7 semble aussi indiquer que la mobilité des gains au Canada pourrait être caractérisée par des mécanismes de transmission assez complexes. Plus particulièrement, différents facteurs d'influence parentale pourraient jouer un rôle dans les différents segments de la répartition. Au bas de la répartition, des facteurs institutionnels — comme le suggéraient les études des pays nordiques — pourraient faciliter la mobilité vers le haut des enfants issus d'un milieu à très faibles gainsNote 15. Le profil estimé pour la majeure partie de la répartition correspondrait globalement à l'hypothèse des contraintes d'emprunt : on s'attend à une relation plus forte entre les fils ayant des gains intermédiaires et les pères ayant des gains intermédiaires parce que ces pères sont plus susceptibles d'être soumis à des contraintes en matière de crédit et de ne pas être en mesure d'investir de façon optimale dans le capital humain de leurs enfants. Le profil correspondant aux segments intermédiaires supérieurs de la répartition pourrait aussi s'expliquer par un resserrement du crédit moins important pour les pères ayant des gains leur permettant d'investir de plus en plus dans le capital humain de leurs enfants. Enfin, les facteurs de transmission pourraient être encore plus complexes au sommet de la répartition, comme l'indiquent les résultats des études publiées antérieurement. Des facteurs autres que l'investissement dans le capital humain, comme le réseau de contacts ou le capital familial, pourraient avoir une plus grande influence sur la transmission intergénérationnelle des gains au sein des familles ayant les gains les plus élevés (Björklund, Roine et Waldenström, 2012; Corak et Piraino, 2011; Kramarz et Skans, 2014).
Il importe toutefois de garder à l'esprit certains points importants lorsqu'on interprète la dynamique au bas de la répartition. Il est possible que, à cette extrémité de la répartition, ce soit la mère qui assume la responsabilité des gains familiaux. Il faut aussi souligner que l'échantillon étudié exclut tous les fils élevés sans père (c.-à-d. par une mère seule), qui sont plus susceptibles de se trouver en situation de faible revenu. En outre, la qualité des données pourrait aussi poser problème, puisque les erreurs de mesure ont souvent tendance à être plus prononcées au bas de la répartition des gains ou du revenu. Un examen plus approfondi des facteurs d'influence et de leur identification s'impose, mais dépasse la portée de la présente analyse.
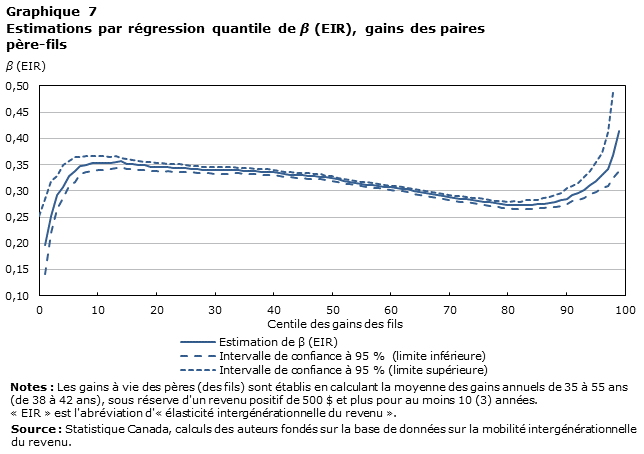
Tableau de données du graphique 7
| Centile des gains des fils | Estimation de β (EIR) | Intervalle de confiance à 95 % (limite inférieure) | Intervalle de confiance à 95 % (limite supérieure) |
|---|---|---|---|
| β (EIR) | |||
| 0 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
| 1 | 0,1969 | 0,1415 | 0,2523 |
| 2 | 0,2519 | 0,2188 | 0,2850 |
| 3 | 0,2915 | 0,2649 | 0,3181 |
| 4 | 0,3073 | 0,2860 | 0,3287 |
| 5 | 0,3290 | 0,3083 | 0,3497 |
| 6 | 0,3370 | 0,3175 | 0,3564 |
| 7 | 0,3479 | 0,3315 | 0,3643 |
| 8 | 0,3501 | 0,3350 | 0,3653 |
| 9 | 0,3524 | 0,3385 | 0,3663 |
| 10 | 0,3528 | 0,3401 | 0,3656 |
| 11 | 0,3532 | 0,3401 | 0,3663 |
| 12 | 0,3537 | 0,3416 | 0,3659 |
| 13 | 0,3543 | 0,3434 | 0,3652 |
| 14 | 0,3561 | 0,3451 | 0,3671 |
| 15 | 0,3516 | 0,3412 | 0,3620 |
| 16 | 0,3505 | 0,3408 | 0,3602 |
| 17 | 0,3496 | 0,3400 | 0,3592 |
| 18 | 0,3489 | 0,3404 | 0,3575 |
| 19 | 0,3461 | 0,3372 | 0,3551 |
| 20 | 0,3459 | 0,3372 | 0,3546 |
| 21 | 0,3450 | 0,3367 | 0,3534 |
| 22 | 0,3454 | 0,3376 | 0,3532 |
| 23 | 0,3439 | 0,3361 | 0,3517 |
| 24 | 0,3431 | 0,3358 | 0,3504 |
| 25 | 0,3432 | 0,3360 | 0,3503 |
| 26 | 0,3421 | 0,3350 | 0,3492 |
| 27 | 0,3408 | 0,3343 | 0,3473 |
| 28 | 0,3401 | 0,3335 | 0,3467 |
| 29 | 0,3394 | 0,3332 | 0,3456 |
| 30 | 0,3392 | 0,3329 | 0,3456 |
| 31 | 0,3390 | 0,3328 | 0,3453 |
| 32 | 0,3388 | 0,3326 | 0,3450 |
| 33 | 0,3394 | 0,3334 | 0,3453 |
| 34 | 0,3393 | 0,3332 | 0,3455 |
| 35 | 0,3382 | 0,3324 | 0,3440 |
| 36 | 0,3372 | 0,3312 | 0,3432 |
| 37 | 0,3373 | 0,3315 | 0,3431 |
| 38 | 0,3366 | 0,3309 | 0,3423 |
| 39 | 0,3359 | 0,3303 | 0,3415 |
| 40 | 0,3350 | 0,3293 | 0,3406 |
| 41 | 0,3334 | 0,3280 | 0,3387 |
| 42 | 0,3321 | 0,3266 | 0,3376 |
| 43 | 0,3308 | 0,3256 | 0,3359 |
| 44 | 0,3302 | 0,3250 | 0,3354 |
| 45 | 0,3294 | 0,3241 | 0,3347 |
| 46 | 0,3285 | 0,3231 | 0,3338 |
| 47 | 0,3278 | 0,3224 | 0,3332 |
| 48 | 0,3268 | 0,3216 | 0,3321 |
| 49 | 0,3257 | 0,3202 | 0,3312 |
| 50 | 0,3237 | 0,3184 | 0,3290 |
| 51 | 0,3221 | 0,3165 | 0,3277 |
| 52 | 0,3187 | 0,3134 | 0,3240 |
| 53 | 0,3170 | 0,3121 | 0,3219 |
| 54 | 0,3155 | 0,3106 | 0,3204 |
| 55 | 0,3138 | 0,3084 | 0,3192 |
| 56 | 0,3120 | 0,3071 | 0,3170 |
| 57 | 0,3112 | 0,3061 | 0,3164 |
| 58 | 0,3096 | 0,3046 | 0,3147 |
| 59 | 0,3080 | 0,3027 | 0,3133 |
| 60 | 0,3065 | 0,3011 | 0,3119 |
| 61 | 0,3048 | 0,2997 | 0,3100 |
| 62 | 0,3040 | 0,2988 | 0,3092 |
| 63 | 0,3025 | 0,2972 | 0,3079 |
| 64 | 0,3002 | 0,2945 | 0,3058 |
| 65 | 0,2978 | 0,2925 | 0,3030 |
| 66 | 0,2959 | 0,2904 | 0,3014 |
| 67 | 0,2941 | 0,2889 | 0,2993 |
| 68 | 0,2923 | 0,2872 | 0,2975 |
| 69 | 0,2897 | 0,2843 | 0,2951 |
| 70 | 0,2877 | 0,2821 | 0,2933 |
| 71 | 0,2859 | 0,2805 | 0,2914 |
| 72 | 0,2840 | 0,2784 | 0,2896 |
| 73 | 0,2837 | 0,2781 | 0,2893 |
| 74 | 0,2822 | 0,2767 | 0,2877 |
| 75 | 0,2800 | 0,2742 | 0,2858 |
| 76 | 0,2795 | 0,2732 | 0,2858 |
| 77 | 0,2780 | 0,2719 | 0,2841 |
| 78 | 0,2771 | 0,2712 | 0,2829 |
| 79 | 0,2746 | 0,2681 | 0,2812 |
| 80 | 0,2732 | 0,2665 | 0,2799 |
| 81 | 0,2720 | 0,2653 | 0,2788 |
| 82 | 0,2725 | 0,2653 | 0,2798 |
| 83 | 0,2723 | 0,2655 | 0,2791 |
| 84 | 0,2738 | 0,2661 | 0,2815 |
| 85 | 0,2742 | 0,2666 | 0,2817 |
| 86 | 0,2749 | 0,2665 | 0,2833 |
| 87 | 0,2774 | 0,2684 | 0,2864 |
| 88 | 0,2793 | 0,2696 | 0,2890 |
| 89 | 0,2819 | 0,2717 | 0,2921 |
| 90 | 0,2847 | 0,2739 | 0,2956 |
| 91 | 0,2926 | 0,2804 | 0,3048 |
| 92 | 0,2956 | 0,2828 | 0,3084 |
| 93 | 0,3006 | 0,2859 | 0,3153 |
| 94 | 0,3101 | 0,2932 | 0,3270 |
| 95 | 0,3179 | 0,2975 | 0,3382 |
| 96 | 0,3301 | 0,3054 | 0,3549 |
| 97 | 0,3406 | 0,3096 | 0,3717 |
| 98 | 0,3683 | 0,3246 | 0,4120 |
| 99 | 0,4131 | 0,3382 | 0,4879 |
| 100 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer |
|
... n'ayant pas lieu de figurer Notes : Les gains à vie des pères (des fils) sont établis en calculant la moyenne des gains annuels de 35 à 55 ans (de 38 à 42 ans), sous réserve d'un revenu positif de 500 $ et plus pour au moins 10 (3) années. « EIR » est l'abréviation d'« élasticité intergénérationnelle du revenu ». Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
|||
5.4 Revenu du marché et revenu total
Le graphique 8 montre les tendances non linéaires dans la persistance intergénérationnelle du revenu du marché (trait discontinu) et du revenu total (trait pointillé). Les résultats de la régression polynomiale (partie A) et de la régression quantile (partie B) sont présentés. En règle générale, malgré les écarts d'ordre de grandeur, les tendances de non-linéarité dans l'ensemble de la répartition sont assez semblables pour les trois mesures du revenu. Comme pour le modèle linéaire, la persistance tend à être plus élevée pour le revenu du marché et le revenu total que pour les gains. C'est notamment le cas tout en haut de la répartition : les fils des pères ayant les revenus les plus élevés sont beaucoup plus susceptibles d'avoir aussi les revenus les plus élevés à l'âge adulte.
Les différences dans la persistance générationnelle des différentes sources de revenus sont toutefois plus visibles dans les résultats de la régression quantile (partie B). Par exemple, la corrélation entre les fils à faible revenu (p. e. ceux du 10e centile) et les pères à faible revenu est plus forte que la corrélation entre les pères à faibles gains et les fils à faibles gains. En outre, la plus grande mobilité dans les segments intermédiaires supérieurs de la répartition est quelque peu limitée en ce qui concerne le revenu du marché et plus encore pour le revenu total. Contrairement aux résultats pour les gains, qui indiquent que certains fils des centiles de gains supérieurs (p. e. ceux du 85e centile) peuvent provenir de divers milieux pour ce qui est des gains, les fils ayant un revenu supérieur sont plus susceptibles d'avoir un père occupant une position semblable dans la répartition du revenu. La persistance du revenu est particulièrement prononcée au sommet de la répartition, puisqu'elle s'établit à 0,51 ou plus dans les deux centiles supérieurs du revenu total des fils. Ces résultats correspondent de façon générale à ceux des études de plus en plus nombreuses qui montrent que les familles nanties sont en mesure d'améliorer le potentiel de revenu de leurs enfants de différentes manières, par exemple au moyen de meilleurs soins, d'études au privé, du transfert des aptitudes pour l'entrepreneuriat et de liens sociaux (p. e. Duncan et Murnane, 2011).
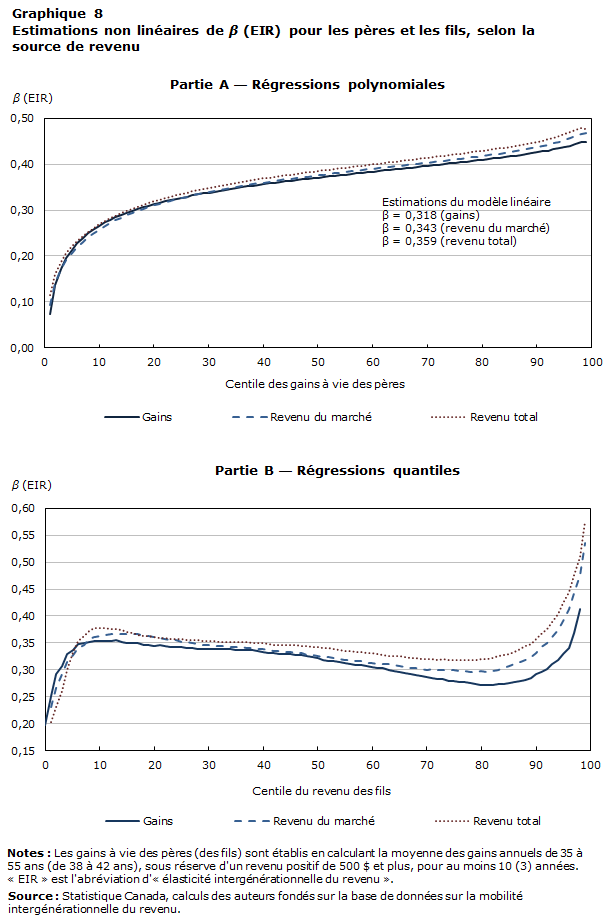
Tableau de données du graphique 8
| Centile | Régressions polynomialesgraphique 8 - note 1 | Régressions quantilesgraphique 8 - note 2 | ||||
|---|---|---|---|---|---|---|
| Gains | Revenu du marché | Revenu total | Gains | Revenu du marché | Revenu total | |
| estimation | ||||||
| 1 | 0,0743 | 0,0940 | 0,1152 | 0,1969 | 0,2301 | 0,2023 |
| 2 | 0,1367 | 0,1421 | 0,1601 | 0,2519 | 0,2666 | 0,2318 |
| 3 | 0,1719 | 0,1713 | 0,1864 | 0,2915 | 0,2922 | 0,2611 |
| 4 | 0,1958 | 0,1911 | 0,2057 | 0,3073 | 0,3150 | 0,2989 |
| 5 | 0,2134 | 0,2067 | 0,2209 | 0,3290 | 0,3278 | 0,3331 |
| 6 | 0,2274 | 0,2201 | 0,2333 | 0,3370 | 0,3412 | 0,3530 |
| 7 | 0,2394 | 0,2312 | 0,2438 | 0,3479 | 0,3469 | 0,3633 |
| 8 | 0,2496 | 0,2410 | 0,2531 | 0,3501 | 0,3573 | 0,3713 |
| 9 | 0,2584 | 0,2497 | 0,2613 | 0,3524 | 0,3612 | 0,3779 |
| 10 | 0,2661 | 0,2576 | 0,2689 | 0,3528 | 0,3624 | 0,3780 |
| 11 | 0,2731 | 0,2649 | 0,2755 | 0,3532 | 0,3645 | 0,3772 |
| 12 | 0,2790 | 0,2714 | 0,2818 | 0,3537 | 0,3660 | 0,3756 |
| 13 | 0,2846 | 0,2776 | 0,2876 | 0,3543 | 0,3662 | 0,3749 |
| 14 | 0,2897 | 0,2833 | 0,2931 | 0,3561 | 0,3667 | 0,3741 |
| 15 | 0,2942 | 0,2885 | 0,2981 | 0,3516 | 0,3672 | 0,3702 |
| 16 | 0,2984 | 0,2934 | 0,3028 | 0,3505 | 0,3668 | 0,3689 |
| 17 | 0,3025 | 0,2979 | 0,3072 | 0,3496 | 0,3660 | 0,3651 |
| 18 | 0,3062 | 0,3022 | 0,3115 | 0,3489 | 0,3633 | 0,3626 |
| 19 | 0,3098 | 0,3062 | 0,3154 | 0,3461 | 0,3634 | 0,3623 |
| 20 | 0,3130 | 0,3101 | 0,3190 | 0,3459 | 0,3613 | 0,3605 |
| 21 | 0,3161 | 0,3137 | 0,3225 | 0,3450 | 0,3585 | 0,3583 |
| 22 | 0,3189 | 0,3171 | 0,3259 | 0,3454 | 0,3565 | 0,3584 |
| 23 | 0,3217 | 0,3203 | 0,3291 | 0,3439 | 0,3551 | 0,3575 |
| 24 | 0,3243 | 0,3234 | 0,3321 | 0,3431 | 0,3549 | 0,3580 |
| 25 | 0,3268 | 0,3264 | 0,3350 | 0,3432 | 0,3521 | 0,3565 |
| 26 | 0,3293 | 0,3292 | 0,3379 | 0,3421 | 0,3516 | 0,3551 |
| 27 | 0,3316 | 0,3320 | 0,3406 | 0,3408 | 0,3493 | 0,3558 |
| 28 | 0,3338 | 0,3346 | 0,3431 | 0,3401 | 0,3486 | 0,3549 |
| 29 | 0,3360 | 0,3371 | 0,3456 | 0,3394 | 0,3467 | 0,3543 |
| 30 | 0,3381 | 0,3394 | 0,3480 | 0,3392 | 0,3458 | 0,3543 |
| 31 | 0,3402 | 0,3417 | 0,3503 | 0,3390 | 0,3449 | 0,3531 |
| 32 | 0,3422 | 0,3439 | 0,3526 | 0,3388 | 0,3439 | 0,3525 |
| 33 | 0,3441 | 0,3461 | 0,3548 | 0,3394 | 0,3436 | 0,3521 |
| 34 | 0,3460 | 0,3482 | 0,3569 | 0,3393 | 0,3426 | 0,3519 |
| 35 | 0,3478 | 0,3502 | 0,3589 | 0,3382 | 0,3424 | 0,3521 |
| 36 | 0,3496 | 0,3522 | 0,3610 | 0,3372 | 0,3416 | 0,3515 |
| 37 | 0,3512 | 0,3542 | 0,3630 | 0,3373 | 0,3407 | 0,3513 |
| 38 | 0,3529 | 0,3560 | 0,3649 | 0,3366 | 0,3398 | 0,3502 |
| 39 | 0,3546 | 0,3579 | 0,3668 | 0,3359 | 0,3389 | 0,3501 |
| 40 | 0,3562 | 0,3596 | 0,3686 | 0,3350 | 0,3382 | 0,3490 |
| 41 | 0,3578 | 0,3614 | 0,3704 | 0,3334 | 0,3369 | 0,3484 |
| 42 | 0,3592 | 0,3631 | 0,3722 | 0,3321 | 0,3358 | 0,3467 |
| 43 | 0,3607 | 0,3648 | 0,3738 | 0,3308 | 0,3349 | 0,3469 |
| 44 | 0,3622 | 0,3664 | 0,3755 | 0,3302 | 0,3337 | 0,3462 |
| 45 | 0,3636 | 0,3680 | 0,3772 | 0,3294 | 0,3327 | 0,3462 |
| 46 | 0,3650 | 0,3695 | 0,3788 | 0,3285 | 0,3314 | 0,3456 |
| 47 | 0,3664 | 0,3711 | 0,3803 | 0,3278 | 0,3308 | 0,3445 |
| 48 | 0,3678 | 0,3726 | 0,3819 | 0,3268 | 0,3284 | 0,3440 |
| 49 | 0,3691 | 0,3741 | 0,3835 | 0,3257 | 0,3267 | 0,3426 |
| 50 | 0,3705 | 0,3756 | 0,3850 | 0,3237 | 0,3260 | 0,3415 |
| 51 | 0,3719 | 0,3770 | 0,3865 | 0,3221 | 0,3244 | 0,3409 |
| 52 | 0,3732 | 0,3785 | 0,3880 | 0,3187 | 0,3236 | 0,3400 |
| 53 | 0,3745 | 0,3799 | 0,3895 | 0,3170 | 0,3220 | 0,3387 |
| 54 | 0,3758 | 0,3813 | 0,3910 | 0,3155 | 0,3201 | 0,3369 |
| 55 | 0,3771 | 0,3827 | 0,3924 | 0,3138 | 0,3188 | 0,3357 |
| 56 | 0,3784 | 0,3842 | 0,3938 | 0,3120 | 0,3178 | 0,3352 |
| 57 | 0,3797 | 0,3855 | 0,3953 | 0,3112 | 0,3169 | 0,3338 |
| 58 | 0,3810 | 0,3869 | 0,3967 | 0,3096 | 0,3156 | 0,3332 |
| 59 | 0,3823 | 0,3883 | 0,3981 | 0,3080 | 0,3131 | 0,3314 |
| 60 | 0,3836 | 0,3897 | 0,3995 | 0,3065 | 0,3123 | 0,3310 |
| 61 | 0,3849 | 0,3911 | 0,4010 | 0,3048 | 0,3106 | 0,3292 |
| 62 | 0,3861 | 0,3925 | 0,4024 | 0,3040 | 0,3103 | 0,3276 |
| 63 | 0,3874 | 0,3938 | 0,4037 | 0,3025 | 0,3099 | 0,3265 |
| 64 | 0,3886 | 0,3952 | 0,4051 | 0,3002 | 0,3086 | 0,3259 |
| 65 | 0,3899 | 0,3966 | 0,4065 | 0,2978 | 0,3072 | 0,3248 |
| 66 | 0,3911 | 0,3979 | 0,4080 | 0,2959 | 0,3056 | 0,3243 |
| 67 | 0,3923 | 0,3992 | 0,4094 | 0,2941 | 0,3037 | 0,3228 |
| 68 | 0,3936 | 0,4006 | 0,4108 | 0,2923 | 0,3025 | 0,3220 |
| 69 | 0,3948 | 0,4019 | 0,4123 | 0,2897 | 0,3014 | 0,3209 |
| 70 | 0,3961 | 0,4033 | 0,4137 | 0,2877 | 0,3001 | 0,3204 |
| 71 | 0,3973 | 0,4047 | 0,4151 | 0,2859 | 0,3006 | 0,3201 |
| 72 | 0,3986 | 0,4061 | 0,4166 | 0,2840 | 0,3002 | 0,3191 |
| 73 | 0,3999 | 0,4075 | 0,4181 | 0,2837 | 0,2997 | 0,3197 |
| 74 | 0,4012 | 0,4089 | 0,4196 | 0,2822 | 0,2990 | 0,3189 |
| 75 | 0,4025 | 0,4104 | 0,4210 | 0,2800 | 0,2988 | 0,3186 |
| 76 | 0,4038 | 0,4118 | 0,4226 | 0,2795 | 0,2986 | 0,3181 |
| 77 | 0,4051 | 0,4133 | 0,4241 | 0,2780 | 0,2974 | 0,3189 |
| 78 | 0,4065 | 0,4148 | 0,4257 | 0,2771 | 0,2960 | 0,3189 |
| 79 | 0,4079 | 0,4163 | 0,4273 | 0,2746 | 0,2964 | 0,3190 |
| 80 | 0,4093 | 0,4179 | 0,4289 | 0,2732 | 0,2972 | 0,3194 |
| 81 | 0,4107 | 0,4195 | 0,4306 | 0,2720 | 0,2966 | 0,3199 |
| 82 | 0,4122 | 0,4211 | 0,4323 | 0,2725 | 0,2978 | 0,3226 |
| 83 | 0,4136 | 0,4228 | 0,4340 | 0,2723 | 0,3004 | 0,3250 |
| 84 | 0,4151 | 0,4245 | 0,4358 | 0,2738 | 0,3033 | 0,3269 |
| 85 | 0,4166 | 0,4262 | 0,4376 | 0,2742 | 0,3064 | 0,3295 |
| 86 | 0,4181 | 0,4280 | 0,4396 | 0,2749 | 0,3114 | 0,3336 |
| 87 | 0,4198 | 0,4299 | 0,4416 | 0,2774 | 0,3144 | 0,3386 |
| 88 | 0,4215 | 0,4320 | 0,4438 | 0,2793 | 0,3183 | 0,3433 |
| 89 | 0,4233 | 0,4342 | 0,4460 | 0,2819 | 0,3245 | 0,3484 |
| 90 | 0,4252 | 0,4364 | 0,4484 | 0,2847 | 0,3318 | 0,3566 |
| 91 | 0,4273 | 0,4389 | 0,4511 | 0,2926 | 0,3417 | 0,3656 |
| 92 | 0,4294 | 0,4417 | 0,4540 | 0,2956 | 0,3496 | 0,3754 |
| 93 | 0,4318 | 0,4447 | 0,4571 | 0,3006 | 0,3617 | 0,3894 |
| 94 | 0,4344 | 0,4483 | 0,4606 | 0,3101 | 0,3740 | 0,4035 |
| 95 | 0,4373 | 0,4519 | 0,4644 | 0,3179 | 0,3898 | 0,4235 |
| 96 | 0,4403 | 0,4563 | 0,4689 | 0,3301 | 0,4124 | 0,4454 |
| 97 | 0,4438 | 0,4615 | 0,4737 | 0,3406 | 0,4421 | 0,4752 |
| 98 | 0,4475 | 0,4662 | 0,4777 | 0,3683 | 0,4765 | 0,5096 |
| 99 | 0,4475 | 0,4671 | 0,4758 | 0,4131 | 0,5359 | 0,5765 |
Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||||||
5.5 Variation et non-linéarités liées au cycle de vie
Comme dans le cas du modèle linéaire simple, il est possible que les tendances de non-linéarité ne soient pas estimées correctement si les biais liés au cycle de vie et aux erreurs dans les variables ne sont pas pris en compte comme il se doit. La distorsion risque d'être plus importante dans la partie supérieure de la répartition, puisque la plupart des enfants ayant des gains à vie élevés n'ont pas encore atteint leur plein potentiel de gains à un jeune âge. Pour valider cette hypothèse, on reprend l'analyse présentée à la section 5.4 en utilisant deux autres définitions des gains à vie des pères et des fils. Dans le premier scénario, les gains à vie des pères correspondent à la moyenne des gains sur cinq ans de 1978 à 1982, alors que les gains des fils sont ceux de l'année où ils ont 30 ans (trait discontinu). Dans le deuxième scénario, la définition des gains des pères est la même, mais on observe les gains des fils à 40 ans (trait pointillé). Comme l'indiquent les résultats à la section 5.4, les deux biais liés au cycle de vie et aux erreurs dans les variables sont susceptibles d'être présents dans le premier scénario, alors que le biais lié au cycle de vie peut être atténué dans le deuxième. Les résultats sont présentés au graphique 9, lequel fournit aussi les estimations privilégiées à titre de référence (trait plein).
De fait, le graphique 9 révèle une tendance très différente de non-linéarité lorsque les gains des fils à 30 ans sont utilisés. Dans le cas des régressions polynomiales, cela entraîne une sous-estimation de la persistance intergénérationnelle dans pratiquement toute la répartition des gains des pères. En raison de la variation liée au cycle de vie, l'importance de la corrélation entre les gains des pères et ceux des fils semble être particulièrement sous-estimée dans la partie supérieure de la répartition. Par exemple, l'élasticité estimée au 95e centile n'est que de 0,24, c'est-à-dire environ 45 % de moins que l'estimation obtenue à partir de la définition privilégiée (0,44). Lorsqu'on réduit le biais lié au cycle de vie en utilisant les gains des fils à 40 ans, la tendance de non-linéarité est presque identique à la tendance obtenue à l'aide du modèle privilégié pour presque toute la répartition. Toutefois, les estimations pour les centiles supérieurs sont quand même inférieures à celles du modèle privilégié parce que la mesure des gains des pères est moins précise.
Les résultats de la régression quantile montrent aussi que le fait de ne pas tenir compte de la variation liée au cycle de vie peut entraîner des tendances de non-linéarité considérablement biaisées. La diminution de la persistance des gains du 15e au 95e centile des gains des fils est beaucoup plus abrupte que celle qu'on obtient dans le modèle privilégié et donne à penser, à tort, que la mobilité augmente jusqu'au 95e centile de la répartition des fils. L'élasticité estimée au 95e centile descend jusqu'à 0,14 lorsque les gains des fils à 30 ans sont utilisés comme mesures indirectes des gains à vie, ce qui constitue 56 % de moins que l'estimation de 0,32 du modèle privilégié. Encore une fois, la tendance de non-linéarité s'apparente davantage à celle du modèle privilégié lorsqu'on utilise les gains des fils à 40 ans. Il est également intéressant de souligner que l'utilisation de moyennes quinquennales sur une période donnée pour les pères entraîne aussi un biais vers le bas dans les estimations par régression quantile pour les grands segments du centre de la répartition des gains des fils.
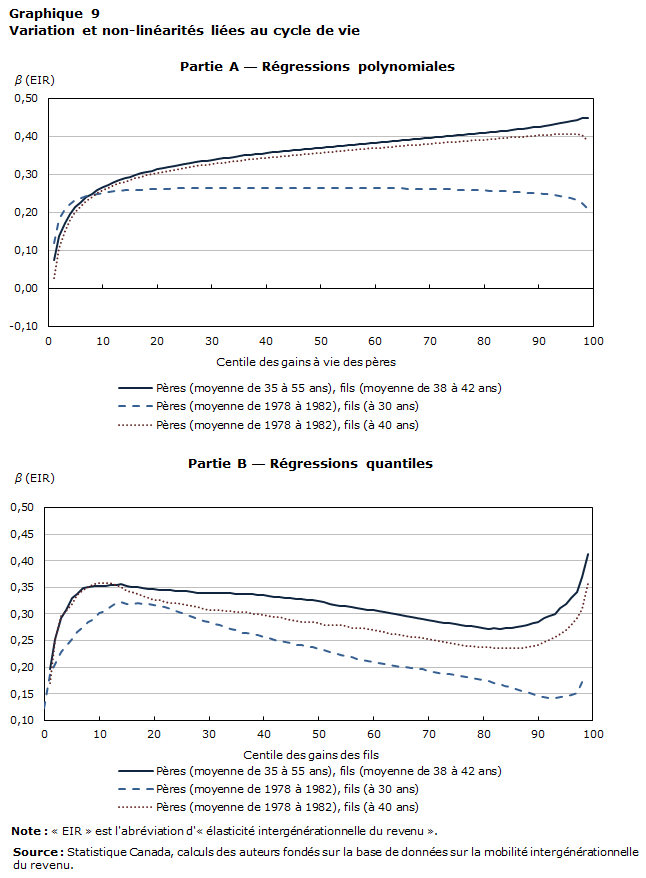
Tableau de données du graphique 9
| Centile | Régressions polynomialesGraphique 9 - note 1 | Régressions quantilesGraphique 9 - note 2 | ||||
|---|---|---|---|---|---|---|
| Pères (moyenne de 35 à 55 ans), fils (moyenne de 38 à 42 ans) | Pères (moyenne de 1978 à 1982), fils (à 30 ans) | Pères (moyenne de 1978 à 1982), fils (à 40 ans) | Pères (moyenne de 35 à 55 ans), fils (moyenne de 38 à 42 ans) | Pères (moyenne de 1978 à 1982), fils (à 30 ans) | Pères (moyenne de 1978 à 1982), fils (à 40 ans) | |
| Estimation de β (EIR) | ||||||
| 1 | 0,0743 | 0,1201 | 0,0287 | 0,1969 | 0,1229 | 0,1703 |
| 2 | 0,1367 | 0,1820 | 0,1074 | 0,2519 | 0,1872 | 0,2504 |
| 3 | 0,1719 | 0,2076 | 0,1504 | 0,2915 | 0,2053 | 0,2960 |
| 4 | 0,1958 | 0,2223 | 0,1793 | 0,3073 | 0,2278 | 0,3045 |
| 5 | 0,2134 | 0,2314 | 0,1999 | 0,3290 | 0,2397 | 0,3184 |
| 6 | 0,2274 | 0,2378 | 0,2161 | 0,3370 | 0,2527 | 0,3352 |
| 7 | 0,2394 | 0,2427 | 0,2294 | 0,3479 | 0,2653 | 0,3443 |
| 8 | 0,2496 | 0,2464 | 0,2403 | 0,3501 | 0,2759 | 0,3495 |
| 9 | 0,2584 | 0,2493 | 0,2497 | 0,3524 | 0,2853 | 0,3564 |
| 10 | 0,2661 | 0,2516 | 0,2576 | 0,3528 | 0,2900 | 0,3579 |
| 11 | 0,2731 | 0,2536 | 0,2647 | 0,3532 | 0,3023 | 0,3573 |
| 12 | 0,2790 | 0,2552 | 0,2709 | 0,3537 | 0,3061 | 0,3575 |
| 13 | 0,2846 | 0,2565 | 0,2762 | 0,3543 | 0,3137 | 0,3539 |
| 14 | 0,2897 | 0,2576 | 0,2811 | 0,3561 | 0,3203 | 0,3503 |
| 15 | 0,2942 | 0,2586 | 0,2857 | 0,3516 | 0,3224 | 0,3436 |
| 16 | 0,2984 | 0,2594 | 0,2898 | 0,3505 | 0,3186 | 0,3402 |
| 17 | 0,3025 | 0,2601 | 0,2935 | 0,3496 | 0,3188 | 0,3380 |
| 18 | 0,3062 | 0,2608 | 0,2972 | 0,3489 | 0,3201 | 0,3336 |
| 19 | 0,3098 | 0,2614 | 0,3004 | 0,3461 | 0,3187 | 0,3293 |
| 20 | 0,3130 | 0,2619 | 0,3035 | 0,3459 | 0,3184 | 0,3264 |
| 21 | 0,3161 | 0,2623 | 0,3064 | 0,3450 | 0,3170 | 0,3258 |
| 22 | 0,3189 | 0,2627 | 0,3092 | 0,3454 | 0,3151 | 0,3225 |
| 23 | 0,3217 | 0,2631 | 0,3118 | 0,3439 | 0,3122 | 0,3210 |
| 24 | 0,3243 | 0,2634 | 0,3144 | 0,3431 | 0,3086 | 0,3199 |
| 25 | 0,3268 | 0,2637 | 0,3168 | 0,3432 | 0,3060 | 0,3183 |
| 26 | 0,3293 | 0,2639 | 0,3191 | 0,3421 | 0,3021 | 0,3171 |
| 27 | 0,3316 | 0,2642 | 0,3213 | 0,3408 | 0,2979 | 0,3144 |
| 28 | 0,3338 | 0,2643 | 0,3233 | 0,3401 | 0,2947 | 0,3120 |
| 29 | 0,3360 | 0,2645 | 0,3253 | 0,3394 | 0,2908 | 0,3091 |
| 30 | 0,3381 | 0,2647 | 0,3273 | 0,3392 | 0,2866 | 0,3080 |
| 31 | 0,3402 | 0,2648 | 0,3292 | 0,3390 | 0,2839 | 0,3078 |
| 32 | 0,3422 | 0,2650 | 0,3310 | 0,3388 | 0,2818 | 0,3063 |
| 33 | 0,3441 | 0,2651 | 0,3328 | 0,3394 | 0,2790 | 0,3057 |
| 34 | 0,3460 | 0,2652 | 0,3346 | 0,3393 | 0,2760 | 0,3053 |
| 35 | 0,3478 | 0,2652 | 0,3363 | 0,3382 | 0,2719 | 0,3038 |
| 36 | 0,3496 | 0,2653 | 0,3379 | 0,3372 | 0,2692 | 0,3029 |
| 37 | 0,3512 | 0,2653 | 0,3394 | 0,3373 | 0,2649 | 0,3028 |
| 38 | 0,3529 | 0,2654 | 0,3409 | 0,3366 | 0,2641 | 0,3006 |
| 39 | 0,3546 | 0,2654 | 0,3424 | 0,3359 | 0,2619 | 0,2990 |
| 40 | 0,3562 | 0,2654 | 0,3439 | 0,3350 | 0,2596 | 0,2971 |
| 41 | 0,3578 | 0,2654 | 0,3453 | 0,3334 | 0,2567 | 0,2954 |
| 42 | 0,3592 | 0,2654 | 0,3467 | 0,3321 | 0,2552 | 0,2940 |
| 43 | 0,3607 | 0,2654 | 0,3480 | 0,3308 | 0,2517 | 0,2934 |
| 44 | 0,3622 | 0,2654 | 0,3494 | 0,3302 | 0,2488 | 0,2911 |
| 45 | 0,3636 | 0,2654 | 0,3507 | 0,3294 | 0,2464 | 0,2888 |
| 46 | 0,3650 | 0,2653 | 0,3520 | 0,3285 | 0,2450 | 0,2869 |
| 47 | 0,3664 | 0,2653 | 0,3533 | 0,3278 | 0,2423 | 0,2854 |
| 48 | 0,3678 | 0,2652 | 0,3546 | 0,3268 | 0,2408 | 0,2841 |
| 49 | 0,3691 | 0,2652 | 0,3559 | 0,3257 | 0,2386 | 0,2838 |
| 50 | 0,3705 | 0,2651 | 0,3571 | 0,3237 | 0,2370 | 0,2819 |
| 51 | 0,3719 | 0,2650 | 0,3583 | 0,3221 | 0,2340 | 0,2797 |
| 52 | 0,3732 | 0,2649 | 0,3596 | 0,3187 | 0,2323 | 0,2791 |
| 53 | 0,3745 | 0,2648 | 0,3609 | 0,3170 | 0,2291 | 0,2794 |
| 54 | 0,3758 | 0,2647 | 0,3621 | 0,3155 | 0,2260 | 0,2781 |
| 55 | 0,3771 | 0,2646 | 0,3633 | 0,3138 | 0,2234 | 0,2763 |
| 56 | 0,3784 | 0,2645 | 0,3645 | 0,3120 | 0,2205 | 0,2742 |
| 57 | 0,3797 | 0,2644 | 0,3657 | 0,3112 | 0,2184 | 0,2736 |
| 58 | 0,3810 | 0,2642 | 0,3669 | 0,3096 | 0,2149 | 0,2732 |
| 59 | 0,3823 | 0,2641 | 0,3681 | 0,3080 | 0,2131 | 0,2716 |
| 60 | 0,3836 | 0,2639 | 0,3692 | 0,3065 | 0,2114 | 0,2692 |
| 61 | 0,3849 | 0,2637 | 0,3704 | 0,3048 | 0,2095 | 0,2679 |
| 62 | 0,3861 | 0,2635 | 0,3716 | 0,3040 | 0,2079 | 0,2653 |
| 63 | 0,3874 | 0,2633 | 0,3727 | 0,3025 | 0,2058 | 0,2627 |
| 64 | 0,3886 | 0,2631 | 0,3738 | 0,3002 | 0,2043 | 0,2620 |
| 65 | 0,3899 | 0,2629 | 0,3749 | 0,2978 | 0,2024 | 0,2601 |
| 66 | 0,3911 | 0,2627 | 0,3760 | 0,2959 | 0,2010 | 0,2589 |
| 67 | 0,3923 | 0,2625 | 0,3771 | 0,2941 | 0,2000 | 0,2567 |
| 68 | 0,3936 | 0,2622 | 0,3782 | 0,2923 | 0,1989 | 0,2560 |
| 69 | 0,3948 | 0,2619 | 0,3793 | 0,2897 | 0,1971 | 0,2540 |
| 70 | 0,3961 | 0,2617 | 0,3804 | 0,2877 | 0,1955 | 0,2533 |
| 71 | 0,3973 | 0,2614 | 0,3816 | 0,2859 | 0,1928 | 0,2507 |
| 72 | 0,3986 | 0,2610 | 0,3827 | 0,2840 | 0,1914 | 0,2492 |
| 73 | 0,3999 | 0,2607 | 0,3838 | 0,2837 | 0,1896 | 0,2474 |
| 74 | 0,4012 | 0,2603 | 0,3849 | 0,2822 | 0,1878 | 0,2461 |
| 75 | 0,4025 | 0,2600 | 0,3861 | 0,2800 | 0,1860 | 0,2435 |
| 76 | 0,4038 | 0,2596 | 0,3872 | 0,2795 | 0,1844 | 0,2418 |
| 77 | 0,4051 | 0,2591 | 0,3883 | 0,2780 | 0,1834 | 0,2397 |
| 78 | 0,4065 | 0,2587 | 0,3893 | 0,2771 | 0,1816 | 0,2390 |
| 79 | 0,4079 | 0,2582 | 0,3905 | 0,2746 | 0,1789 | 0,2383 |
| 80 | 0,4093 | 0,2577 | 0,3916 | 0,2732 | 0,1773 | 0,2380 |
| 81 | 0,4107 | 0,2572 | 0,3927 | 0,2720 | 0,1756 | 0,2370 |
| 82 | 0,4122 | 0,2566 | 0,3938 | 0,2725 | 0,1730 | 0,2355 |
| 83 | 0,4136 | 0,2560 | 0,3949 | 0,2723 | 0,1707 | 0,2349 |
| 84 | 0,4151 | 0,2553 | 0,3960 | 0,2738 | 0,1687 | 0,2350 |
| 85 | 0,4166 | 0,2546 | 0,3971 | 0,2742 | 0,1651 | 0,2349 |
| 86 | 0,4181 | 0,2539 | 0,3982 | 0,2749 | 0,1627 | 0,2361 |
| 87 | 0,4198 | 0,2530 | 0,3993 | 0,2774 | 0,1590 | 0,2364 |
| 88 | 0,4215 | 0,2521 | 0,4005 | 0,2793 | 0,1556 | 0,2372 |
| 89 | 0,4233 | 0,2511 | 0,4015 | 0,2819 | 0,1523 | 0,2392 |
| 90 | 0,4252 | 0,2500 | 0,4025 | 0,2847 | 0,1492 | 0,2423 |
| 91 | 0,4273 | 0,2486 | 0,4036 | 0,2926 | 0,1463 | 0,2468 |
| 92 | 0,4294 | 0,2472 | 0,4046 | 0,2956 | 0,1443 | 0,2510 |
| 93 | 0,4318 | 0,2455 | 0,4055 | 0,3006 | 0,1419 | 0,2563 |
| 94 | 0,4344 | 0,2434 | 0,4063 | 0,3101 | 0,1427 | 0,2614 |
| 95 | 0,4373 | 0,2407 | 0,4069 | 0,3179 | 0,1432 | 0,2699 |
| 96 | 0,4403 | 0,2373 | 0,4071 | 0,3301 | 0,1451 | 0,2797 |
| 97 | 0,4438 | 0,2324 | 0,4062 | 0,3406 | 0,1474 | 0,2921 |
| 98 | 0,4475 | 0,2248 | 0,4029 | 0,3683 | 0,1521 | 0,3094 |
| 99 | 0,4475 | 0,2081 | 0,3885 | 0,4131 | 0,1712 | 0,3581 |
Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
||||||
Enfin, soulignons que Corak et Heisz (1999) ont aussi examiné la nature des non-linéarités dans la persistance intergénérationnelle des gains au Canada. Ils ont estimé un modèle non paramétrique souple à partir de l'ancienne version de la base de DMIR. Bien qu'une comparaison directe avec les résultats de la présente analyse ne soit pas possible en raison des différentes formes fonctionnelles employées, il est intéressant de souligner que Corak et Heisz (1999) ont aussi constaté une augmentation considérable de l'élasticité estimée au sommet de la répartition (au-dessus du 99e centile). Contrairement aux résultats obtenus dans la présente analyse, toutefois, ils ont trouvé une persistance moindre se situant tout juste sous le 99e centile comparativement à l'EIR estimée pour la majorité des segments supérieurs de la répartition. Il est difficile de dire si la différence est attribuable aux différentes formes fonctionnelles employées dans les deux études ou à l'ensemble de données améliorées utilisé dans la présente étude, qui tient mieux compte de la variation des gains liée au cycle de vie. Toutefois, les résultats présentés au graphique 9 indiquent que des mesures indirectes inexactes des gains à vie peuvent déformer considérablement les tendances de non-linéarité estimées dans la transmission intergénérationnelle des gains.
6 Conclusion
Il est utile de comprendre l'ampleur de la mobilité intergénérationnelle des gains et du revenu aux fins des politiques économiques et sociales. Plus particulièrement, les estimations de l'élasticité intergénérationnelle du revenu (EIR) sont souvent considérées comme des indicateurs généraux de l'égalité des chances. Toutefois, comme on ne dispose généralement pas de données historiques sur la totalité de la vie active des parents et de leurs enfants, bon nombre des estimations actuelles de l'EIR dans divers pays pourraient être concernés par les biais découlant de mesures indirectes inexactes des gains à vie. La présente étude réexamine la mesure dans laquelle la variation liée au cycle de vie et les erreurs dans les variables peuvent biaiser les estimations de l'EIR, aussi bien en ce qui concerne la moyenne que dans les différents centiles de la répartition du revenu. La nouvelle version augmentée de la base de données canadienne sur la mobilité intergénérationnelle du revenu, qui comporte des données presque complètes sur la vie active, contribuera à approfondir les connaissances à ce sujet.
L'analyse montre qu'un biais lié au cycle de vie peut se manifester à n'importe quelle étape de la vie active. Le biais tend à être plus élevé lorsque les gains annuels en début de vie active sont utilisés pour produire une mesure indirecte des gains à vie comme variable dépendante. Cette constatation correspond aux résultats obtenus à l'échelle internationale. Toutefois, l'étude montre aussi qu'il existe des différences entre les pays en ce qui concerne l'âge auquel le biais lié au cycle de vie est minimal. Cette constatation fait ressortir la difficulté de faire des comparaisons appropriées entre pays même si l'on tient compte des différences dans l'échantillon et dans la méthodologie, c'est-à-dire qu'il peut toujours y avoir une variation d'un pays à l'autre des estimations de l'EIR à cause des différents âges auxquels les gains des fils sont observés.
L'élasticité intergénérationnelle des gains au Canada est estimée à environ 0,32, une valeur supérieure à l'estimation approximative de 0,2 qu'on trouve dans les publications canadiennes. La prise en compte du biais lié au cycle de vie auquel sont soumises les premières estimations explique environ les deux tiers de la divergence, alors que le biais induit par les erreurs dans les variables rend compte du dernier tiers. L'étude montre que le biais est plus grand pour le revenu du marché et le revenu total que pour les gains seuls. Les résultats révèlent également des différences notables entre les sexes en ce qui concerne l'effet de ces biais sur les EIR estimées. L'élasticité père-fille demeure assez modeste, quel que soit l'âge auquel on observe les gains des filles. L'EIR plus faible pour les filles pourrait s'expliquer par des différences entre les sexes en matière de participation au marché du travail ainsi que par des problèmes d'estimation découlant de l'assortiment conjugal. Il serait donc utile d'examiner de plus près ces tendances dans le cadre de futures recherches.
En utilisant des données moins touchées par des erreurs de mesure que celles qui ont servi à réaliser les études précédentes, la présente analyse explique une tendance distincte de non-linéarité dans la transmission intergénérationnelle du revenu au Canada. Les résultats montrent que la relation entre les gains des pères et ceux des fils se présente sous la forme d'une courbe plutôt convexe, un résultat semblable à celui qui ressort d'études réalisées dans des pays de l'Europe du Nord, mais qui fait contraste avec la tendance linéaire observée aux États-Unis. Les régressions polynomiales et quantiles révèlent des taux de mobilité élevés tout en bas de la répartition, et une mobilité faible en haut. Les institutions sociales pourraient avoir un rôle à jouer dans ces constatations. En outre, l'étude montre que les tendances de non-linéarité peuvent être considérablement mal interprétées lorsque le biais lié au cycle de vie et le biais lié aux erreurs dans les variables ne sont pas pris en compte comme il se doit, particulièrement dans la partie supérieure de la répartition.
Annexe
| Âge en 1978 | Répartition | Gains moyens de 1978 à 1982 | |
|---|---|---|---|
| nombre | pourcent | dollars constants de 2010 | |
| 34 ans ou moins | 27 001 | 5,34 | 46 557 |
| 35 à 40 ans | 137 263 | 27,13 | 53 509 |
| 41 à 45 ans | 143 230 | 28,31 | 55 282 |
| 46 à 50 ans | 108 582 | 21,46 | 54 202 |
| 51 ans et plus | 89 910 | 17,77 | 49 252 |
| Total | 505 986 | 100,00 | 53 155 |
|
Notes : L'échantillon comprend tous les pères (de fils et de filles) associés à la cohorte de 1982 de la base DMIR. Comme les chiffres ont été arrondis, leur somme peut ne pas correspondre aux totaux indiqués. Source : Statistique Canada, calculs des auteurs fondés sur la base de données sur la mobilité intergénérationnelle du revenu. |
|||
| Nom | Cohorte de naissance du père | Père âgé de 35 ans | Père âgé de 55 ans | Âge du père (en années) | Nombre d'enregistrements de 35 à 55 ans | Nombre d'enregistrements avec gains >=500 $ | Enregistrements utilisés | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | |||||||
| A | 1925 | 1960 | 1980 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | edNote 1 | edNote 1 | edNote 1 | 3 | 3 | Non |
| B | 1935 | 1970 | 1990 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | 13 | 13 | Oui |
| C | 1940 | 1975 | 1995 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | GNote 2 | GNote 2 | edNote 1 | edNote 1 | edNote 1 | 18 | 16 | Oui |
| D | 1943 | 1978 | 1998 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | 21 | 21 | Oui |
| E | 1944 | 1979 | 1999 | edNote 1 | edNote 1 | GNote 2 | edNote 1 | edNote 1 | GNote 2 | GNote 2 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | GNote 2 | edNote 1 | edNote 1 | GNote 2 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | GNote 2 | 21 | 15 | Oui |
| F | 1950 | 1985 | 2005 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 15 | 15 | Oui |
| G | 1950 | 1985 | 2005 | edNote 1 | edNote 1 | edNote 1 | GNote 2 | GNote 2 | GNote 2 | GNote 2 | edNote 1 | edNote 1 | edNote 1 | GNote 2 | GNote 2 | edNote 1 | GNote 2 | GNote 2 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 15 | 7 | Non |
| H | 1955 | 1990 | 2010 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 10 | 10 | Oui |
| I | 1960 | 1995 | 2015 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | edNote 1 | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | Note ...: n'ayant pas lieu de figurer | 5 | 5 | Non |
... n'ayant pas lieu de figurer
|
|||||||||||||||||||||||||||
References
Aina, C. et C. Nicoletti. 2013. The intergenerational transmission of liberal professions: nepotism versus abilities. Document non publié.
Baker, M. et G. Solon. 2003. « Earnings Dynamics and Inequality among Canadian Men, 1976-1992: Evidence from Longitudinal Income Tax Records ». Journal of Labor Economics 21 (2) : 289 à 321.
Becker, G.S. et N. Tomes. 1986. « Human Capital and the Rise and Fall of Families ». Journal of Labor Economics 4 (3) : S1 à S39.
Björklund, A. 1993. « A Comparison between Actual Distributions of Annual and Lifetime Income: Sweden 1951-89 ». Review of Income and Wealth 39 (4) : 377 à 386.
Björklund, A. et M. Jäntti. 2010. « Intergenerational Income Mobility and the Role of Family Background ». Dans Oxford Handbook of Economic Inequality, publié sous la direction de W. Salverda, B. Nolan et T. Smeeding. Oxford : Oxford University Press.
Björklund, A., J. Roine et D. Waldenström. 2012. « Intergenerational top income mobility in Sweden: Capitalistic dynasties in the land of equal opportunity? ». Journal of Public Economics 96 (5-6) : 474 à 484.
Böhlmark, A. et M.J. Lindquist. 2006. « Life-Cycle Variations in the Association between Current and Lifetime Income: Replication and Extension for Sweden ». Journal of Labor Economics 24 (4): 879 à 900.
Bratsberg, B., K. Røed, O. Raaum, R. Naylor, M. Jäntti, T. Eriksson et E. Österbacka. 2007. « Nonlinearities in Intergenerational Earnings Mobility: Consequences for Cross-Country Comparisons ». The Economic Journal 117 : C72 à C92.
Brenner, J. 2010. « Life-Cycle Variations in the Association between Current and Lifetime Earnings: Evidence for German Natives and Guest Workers ». Labour Economics 17 (2) : 392 à 406.
Chadwick, L. et G. Solon. 2002. « Intergenerational Income Mobility among Daughters ». The American Economic Review 92 (1) : 335 à 344.
Chetty, R., N. Hendren, P. Kline et E. Saez. 2014. « Where is the Land of Opportunity? The Geography of Intergenerational Mobility in the United States ». The Quarterly Journal of Economics 129 (4) : 1553 à 1623.
Corak, M. 2001. « Are the Kids All Right? Intergenerational Mobility and Child Well-Being in Canada ». Dans Review of Economic Performance and Social Progress, publié sous la direction de K. Banting, A. Sharpe et F. St-Hilaire, p. 273 à 292. Montréal et Ottawa : Institut de recherche en politiques et Centre d'étude des niveaux de vie.
Corak, M. 2006. « Do Poor Children Become Poor Adults? Lessons from a Cross Country Comparison of Generational Earnings Mobility ». Dans Research on Economic Inequality, publié sous la direction de J. Creedy et G. Kalb, vol. 13 (1), p. 143 à 188. Amsterdam : Elsevier B.V.
Corak, M. 2013. Income Inequality, Equality of Opportunity, and Intergenerational Mobility. Document de travail de l'IZA no 7520. Bonn : The Institute for the Study of Labor (IZA).
Corak, M., B. Gustafsson et T. Österberg. 2004. « Intergenerational Influences on the Receipt of Unemployment Insurance in Canada and Sweden ». Dans Generational income mobility in North America and Europe, publié sous la direction de M. Corak. Cambridge, R.-U. : Cambridge University Press.
Corak, M. et A. Heisz. 1999. « The Intergenerational Earnings and Income Mobility of Canadian Men: Evidence from Longitudinal Income Tax Data ». The Journal of Human Resources 34 (3) : 504 à 533.
Corak, M., M. Lindquist et B. Mazumder. 2014. « A Comparison of Upward and Downward Intergenerational Mobility in Canada, Sweden and the United States ». Labour Economics 30 (C) : 185 à 200.
Corak, M. et P. Piraino. 2011. « The Intergenerational Transmission of Employers ». Journal of Labor Economics 29 (1) : 37 à 68.
Duncan, G.J. et R.J. Murnane. 2011. « Introduction: The American Dream, Then and Now ». Dans Whither Opportunity? Rising Inequality, Schools, and Children's Life Chances, publié sous la direction de G.J. Duncan et R.J. Murnane. New York : Russell Sage Foundation.
Dunn, T. et D. Holtz-Eakin. 2000. « Financial Capital, Human Capital, and the Transition to Self-Employment: Evidence from Intergenerational Links ». Journal of Labor Economics 18 (2) : 282 à 305.
Ermisch, J., M. Francesconi et T. Siedler. 2005. Intergenerational Economic Mobility and Assortative Mating. Document de travail no 1847. Bonn : The Institute for the Study of Labor (IZA).
Fortin, N. et S. Lefebvre. 1998. « Mobilité intergénérationnelle du revenu au Canada ». Dans Les marchés du travail, les institutions sociales et l'avenir des enfants au Canada, publié sous la direction de M. Corak. Produit no 89-553-X au catalogue de Statistique Canada. Ottawa : Statistique Canada.
Gouskova, E., N. Chiteji et F. Stafford. 2010. « Estimating the intergenerational persistence of lifetime earnings with life course matching: Evidence from the PSID ». Labour Economics 17 (3) : 592 à 597.
Grawe, N.D. 2004. « Reconsidering the Use of Nonlinearities in Intergenerational Earnings Mobility as a Test for Credit Constraints ». Journal of Human Resources 39 (3) : 813 à 827.
Grawe, N.D. 2006. « Lifecycle bias in estimates of intergenerational earnings persistence ». Labour Economics 13 (5) : 551 à 570.
Haider, S. et G. Solon. 2006. « Life-Cycle Variation in the Association between Current and Lifetime Earnings ». The American Economic Review 96 (4) : 1308 à 1320.
Han, S. et C.B. Mulligan. 2001. « Human Capital, Heterogeneity and Estimated Degree of Intergenerational Mobility ». The Economic Journal 111 (470) : 207 à 243.
Kramarz, F. et O.N. Skans. 2014. « When Strong Ties are Strong: Networks and Youth Labour Market Entry ». The Review of Economic Studies 81 : 1164 à 1200.
Lentz, B.F. et D.N. Laband. 1990. « Entrepreneurial Success and Occupational Inheritance among Proprietors ». Canadian Journal of Economics 23 (3) : 563 à 579.
Mazumder, B. 2005. « Fortunate Sons: New Estimates of Intergenerational Mobility in the United States Using Social Security Earnings Data ». The Review of Economics and Statistics 87 (2) : 235 à 255.
Mulligan, C.B. 1997. Parental Priorities and Economic Inequality. Chicago : University of Chicago Press.
Nybom, M. et J. Stuhler. 2011. « Heterogeneous Income Profiles and Life-Cycle Bias in Intergenerational Mobility Estimation ». Document de travail no 5697. Bonn : The Institute for the Study of Labor (IZA).
Oreopoulos, P. 2003. « The long-run consequences of growing up in a poor neighborhood ». Quarterly Journal of Economics 118 : 1533 à 1575.
Oreopoulos, P., M. Page et A.H. Stevens. 2008. « The intergenerational effects of worker displacement ». Journal of Labor Economics 26 : 455 à 484.
Page, M.E. 2004. « New Evidence on Intergenerational Correlations in Welfare Participation ». Dans Generational income mobility in North America and Europe, publié sous la direction de M. Corak. Cambridge, R.-U. : Cambridge University Press.
Pérez-González, F. 2006. « Inherited Control and Firm Performance ». American Economic Review 96 (5) : 1559 à 1588.
Raaum, O., B. Bratsberg, K. Røed, E. Österbacka, T. Eriksson, M. Jäntti et R.A. Naylor. 2007. « Marital sorting, household labor supply and intergenerational earnings mobility across countries ». The B.E. Journal of Economic Analysis and Policy 7 (2) : article no 7.
Roemer, J.E. 1998. Equality of opportunity. Cambridge, Massachusetts : Harvard University Press.
Statistique Canada. 2010. Intergenerational Income Data Reference Manual. Document non publié. Ottawa.
Solon, G. 1992. « Intergenerational Income Mobility in the United States ». American Economic Review 82 (3) : 393 à 408.
Solon, G. 1999. « Intergenerational Mobility in the Labor Market ». Dans Handbook of labor economics, publié sous la direction de O.C. Ashenfelter et D. Card, vol. 3A, p. 1761 à 1800. Amsterdam : Elsevier Science B.V.
Solon, G. 2002. « Cross-country differences in intergenerational earnings mobility ». Journal of Economic Perspectives 16 (3) : 59 à 66.
Sorensen, J.B. 2004. Closure and Exposure: Mechanisms in the Intergenerational Transmission of Self-employment. Document non publié.
- Date de modification :