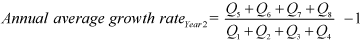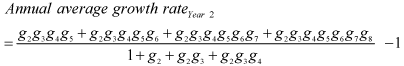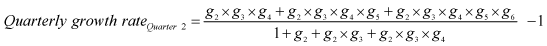Section 3: Features articles
Archived Content
Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please "contact us" to request a format other than those available.
The relationship between monthly, quarterly, and annual growth rates
by Philip Cross and Diana Wyman 1
Growth rates have a distinct dynamic: monthly growth rates have a fixed statistical relationship with quarterly growth rates, and quarterly growth rates have a fixed statistical relationship with the annual average growth rate. However, these relationships are not well understood by analysts or statisticians. While analysts occasionally make references that show an intuitive understanding of the dynamic, a fuller appreciation is required to understand how individual quarters (or months) specifically affect annual (or quarterly) averages. 2 Such knowledge helps analysts monitor how the economy is performing in a particular year without having every data point for that year, and understand why a particularly weak or strong first quarter of the year has a disproportionate impact on that year's annual growth rate.
This paper will explain the principles of growth rate relationships conceptually and mathematically by thoroughly examining the relationship between quarterly growth rates and annual average growth rates. It then applies these principles to how monthly growth relates to quarterly growth rates as well as to data with other frequencies, such as monthly growth rates and annual average growth rates and annual average growth rates and decade growth rates.
A primer on annual average growth
The annual average growth rate answers the question of what happened during one year relative to the year before. It is calculated as the percentage change between two consecutive annual levels. 3 These annual levels are the sum of the four quarterly levels of the two adjacent years, or the average if the data has been annualized. 4 The annual average growth rate does not only reflect what happened during the four quarters of one calendar year, but is affected by the pattern of quarterly growth in both years.
Annual average growth rates are calculated mainly by statistical agencies. For major economic indicators, such as real gross domestic product (GDP) and the consumer price index (CPI), annual growth is a baseline measure of how the economy is performing and how prices are changing. The annual average change in the CPI is the best-known annual average, as it is used to index the entire tax and transfer payment system as well as many wage contracts across the country. Given the significance of the annual average growth of these indicators, it is important to understand the mechanics involved in the calculation of this measure.
Outside of statistical agencies, the year-over-year growth, such as fourth-quarter-over-fourth-quarter or December-over-December change, is the more common measure of growth. Year-over-year growth rates are universally used in business reports, and show the change that occurred during the previous four quarters or twelve months, reflecting only events that occur during the calendar year. Identifying the trend that dominated either the previous four quarters or twelve months is useful for analyzing shorter-term trends, but the trade-off is the greater volatility of the year-over-year change. The year-over-year measures are susceptible to irregular events occurring in either of the two periods being compared, which may distort the identification of the underlying trend.
Figure 3.1 shows the additional volatility of the year-over-year measure compared to the annual average change for the CPI. In September 2005, for example, gasoline prices rose sharply as a result of the disruption of crude oil production in the US following Hurricane Katrina. This price increase affected the year-over-year change in the CPI in both September 2005 (when gasoline prices jumped 35%) and September 2006 (prices fell 19% compared with their spike a year earlier). While the year-over-year measure can quickly signal a shift in the underlying trend, it may provide a false signal that prices (or the economy) are accelerating or decelerating when it is actually an irregular event in the data for the current month or in the data for one year earlier that is causing the change.
Annual average growth more accurately reflects longer-term economic trends by comparing how all of the current year relates to the whole year before it. By integrating two full years of data points, the impact of irregular events is minimized, thereby emphasizing the underlying trend. In the case of 2005 and 2006, when the monthly year-over-year change was so volatile, the annual average growth rate of the CPI was remarkably stable at about 2%, versus the swing from 3.2% to 0.7% in the year-over-year measures. 5 It is this greater stability of the underlying trend that makes the annual average growth rate of the CPI the better measure for indexing wages and the tax and transfer payment system and the reason why statistical agencies calculate annual growth for most of the major economic indicators. 6
Relationship between quarterly growth and annual average growth: the concept
It is worth studying a hypothetical example to outline some of the basic principles of how annual average growth rates are determined. Figure 3.2 shows sales in a hypothetical industry rising steadily through year 1, from $100 billion (at annual rates) in the first quarter to $106 billion in the fourth quarter. The quarterly levels throughout year 2 remain unchanged, at $106 billion. This demonstrates the difference between annual average growth and fourth-quarter-over-fourth-quarter growth rates: there is zero growth between the fourth quarter of year 1 and the fourth quarter of year 2, but the annual average level of sales of $106 billion in year 2 is 2.9% above their average level of $103 billion in year 1. This is because the above-average level at the end of year 1 was maintained throughout year 2.
Figure 3.2 was a hypothetical example contrived to demonstrate how developments during a calendar year relate to the annual average for that year. Figure 3.3 shows these features in actual GDP data. Real GDP rose steadily throughout the four quarters of 2007. Output then leveled off in the first three quarters of 2008, before a large drop in the fourth quarter of the year, which left it 0.7% below the level of the fourth-quarter of 2007. Even though there were only two quarters during 2008 that posted a gain (totaling 0.3%), the average level of GDP in 2008 was $1,320 billion, or 0.7% above its average level of $1,311 billion in 2007. This was the result of the relatively high level of output reached late in 2007 being sustained through most of 2008.
Two basic principles are introduced by the examples of annual average growth in Figures 2 and 3. The first, and most important, is that annual growth rates reflect the pattern of growth in both the year being studied (year 2, or 2008 in the examples) and the previous year (year 1, or 2007, in the examples). The second is that while individual quarterly growth rates have an equal impact on the year-over-year change, they do not have an equal impact on the annual average growth rate; there is a hierarchy for which quarters have the most impact on annual average growth.
The hierarchy of the impact of quarterly growth rates on the annual average growth rate is a characteristic of growth rate dynamics. When an increase (or decrease) occurs in a quarter in either year 1 or 2, it raises (or lowers) the level on which all future increases (or decreases) are based. The growth rate of the first quarter of year 1 has no effect on the annual growth rate between years 1 and 2 because it affects the levels in both years equally. A change in the first quarter of year 2 has the largest impact on annual growth, as it raises (or lowers) the level on which all future changes within year 2 are based, while having no effect whatsoever on the level in year 1. Next to the first quarter of year 2, the growth rates of the two quarters adjacent to the first quarter of year 2 have the second-largest impact. The impact of quarters on annual average growth declines as they move away from the first quarter of year 2 until the second quarter of year 1 and the final quarter of year 2, which have the smallest impact. This hierarchy, which takes the shape of a pyramid, is mathematically demonstrated in the next section.
Relationship between quarterly growth and annual average growth: the math
The annual growth rate of year 2 is calculated as the ratio between the sum of the four most recent quarterly levels and the sum of the previous four quarterly levels. The four quarterly levels of year 1 are Q1, Q2, Q3, and Q4; the four quarterly levels of year 2 are Q5, Q6, Q7, and Q8. The annual average growth rate calculated with levels can be expressed as:
The level in the first quarter of year 1 (Q1) can be calculated by multiplying its growth rate (g1) by the quarterly level that preceded it, referred to as Q0. The level Q2 can be calculated by multiplying its growth rate (g2) and the growth rate in the first quarter of year 1 (g1) by the base level (Q0). Each quarterly level can therefore be expressed in terms of quarterly growth rates multiplied by the level in the base quarter (Q0). The quarterly growth rates of year 1 are referred to as g1, g2, g3, and g4, while the four quarters of year 2 are labeled g5, g6, g7, and g8. The level in the first quarter of year 2, Q5, for example, can therefore be replaced by Q0 x g1 x g2 x g3 x g4 x g5, which describes the base level (Q0) multiplied by the growth rates of the preceding four quarters along with its own growth rate. The quarterly levels Q1 thru Q8can be expressed as:
- Q1 = Q0 x g1
- Q2 = Q0 xg1xg2
- Q3 = Q0xg1xg2xg3
- Q4 = Q0xg1xg2xg3xg4
- Q5= Q0xg1xg2xg3xg4xg5
- Q6 = Q0xg1xg2xg3xg4xg5x g6
- Q7= Q0xg1xg2xg3 xg4xg5xg6xg7
- Q8= Q0xg1xg2xg3xg4xg5x g6xg7xg8
This results in the new equation:
After factoring out and cancelling the term Q0g1 (as it appears in each quarterly expression), the final equation shows the make-up of the four quarterly levels of year 2 in the numerator and the three relevant quarterly levels of year 1 in the denominator expressed as growth rates. 7 Therefore, the algebraic equation of the relationship between quarterly growth rates and annual average growth rates that expresses the annual average growth rate as a function of the quarterly growth rates in year 1 and 2 is 8 :
The hierarchy in which quarterly growth rates contribute to annual average growth is apparent in this equation. In particular, the growth rate of the first quarter of the first year (g1) has no effect on the annual average growth rate in year 2, as shown by its disappearance from the equation. The recurrence of the first quarter of year 2 (g5) four times in the numerator reflects its primary importance in determining the annual average growth rate, as higher (or lower) growth in this quarter compounds throughout year 2.
The impact on annual average growth diminishes according to the distance a quarter is from the first quarter of year 2 (g5); this impact is reflected in either the quarters' increased appearance in the denominator (as occurs for g2, g3, and g4) or their decreased recurrence in the numerator (g6, g7, and g8). The quarterly growth rates on either side of the first quarter of year 2, namely the fourth quarter of year 1 (g4) and the second quarter of year 2 (g6), have the next-largest impact after g5. Growth in the fourth quarter of year 1, g4, compounds throughout year 2; however, the presence of g4 in the denominator means that its growth also affects year 1 and reduces the impact of the quarter on growth in year 2. For the second quarter of year 2, g6, the compounding is not as prevalent as for g5 as a result of its later placement in the year; it repeats only three times in the equation. The impact continues to decline for the third quarter of year 1, g3, and for the third quarter in year 2, g7, as a result of the repetition of g3 in the denominator and g7 compounding only for the last two quarters of year 2. The second quarter of year 1 (g2) appears only one more time in the numerator than the denominator, as its growth affects year 1 nearly as much as year 2, while the fourth quarter of year 2 (g8) appears only once in the numerator; therefore, these two quarters have the least impact in determining the annual growth rate in year 2.
The algebraic equation highlights that there is a hierarchy to the impact of the quarterly growth rate on annual average growth, but it does not show the specific impact that each quarter has on the annual average growth rate. However, the impact can be calculated by inputting into the equation a 1% quarterly growth rate sequentially into all 7 quarters into the equation and setting growth at zero in all other quarters. The resulting change to annual average growth in year 2 is shown in Table 3.1. 9
In the hypothetical scenarios set out in Table 3.1, a 1% increase in the first quarter of year 1 results in annual average growth in year 2 remaining at zero; there is no impact on the annual growth rate in year 2. If the 1% increase occurs in the second quarter of year 1, the annual growth rate in year 2 is 0.25%, indicating that one-quarter of the 1% gain was passed on to the annual growth rate. 10 This continues to increase each quarter by increments of 25% until the maximum pass-through of 100% is attained in the first quarter of year 2, g5. The pass-through then falls by increments of 25% until the fourth quarter of year 2. Figure 3.4 shows the pyramid-shaped hierarchy of the impact of quarterly growth on the annual growth rate and highlights the rate at which growth is passed through from the individual quarters to the annual growth rate, which determines the impact. 11
If the 1% growth occurred in every one of these quarters, as shown in Table 3.2, the result would be an annual average growth rate of 4.1%. By observing the change in the annual growth rate after the addition of just one more quarterly growth rate into the equation, the share of the annual growth rate accounted for by that quarter can be calculated. The first quarter of year 2 accounts for 25% of the annual average growth rate, the largest weight of any quarter. The share falls steadily by about 6 percentage points a quarter as the quarters move away from the first quarter of year 2. At the end of the second quarter of year 2, the cumulative share shows that 81% of the annual growth rate has been determined, even though the year is only half over. 12 Once the third quarter of year 2 is known, 94% of the annual growth rate has been determined, as shown in Figure 3.5. 13
Relationship between monthly growth rates and quarterly growth rates
A similar fixed statistical relationship exists between monthly growth rates and quarterly growth rates. Quarterly growth rates reflect the pattern of monthly growth in both the quarter being measured (quarter 2) and the previous quarter (quarter 1) to which it is being compared. There is a hierarchy for the impact of the individual monthly growth rates on the quarterly growth rate, with the first month of quarter 2 having the largest impact on the growth in quarter 2. The months on either side have the next-largest impact, and the months next to those have the least impact. Growth in the first month of quarter 1 has no impact on growth in quarter 2.
With g2 representing the second month in quarter 1's growth rate, g3the final month in quarter 1's growth rate, g4 the first month of quarter 2's growth rate, g5 the second month of quarter 2's growth rate, and g6 the final month of quarter 2's growth rate, the equation for quarterly growth using monthly growth rates is:
By isolating a 1% increase in each month, the specific impact of the individual months on quarterly growth can be divided into thirds: 100% of the growth rate of the first month of quarter 2 passes through to the quarterly growth rate in quarter 2; 66% of the growth rate of the third month of quarter 1 and the second month of quarter 2 passes through to the quarterly growth rate in quarter 2; and 33% of the growth rate in the second month of quarter 1 and the third month of quarter 2 is passed on to the quarterly growth rate in quarter 2. The pyramid-shaped hierarchy of impact of monthly growth on quarterly growth (measured by the rate at which growth is passed through from the monthly to the quarterly growth rate) is shown in Figure 3.6. The share of the quarterly growth rate accounted for by the first month of quarter 2 is 33%; this figure falls by 11 percentage point intervals equally to right and left as the months move away from this pivotal month. As shown in Figure 3.7, the result is that, after growth in the first month of quarter 2 is published, two-thirds of the quarterly growth rate has been determined: after the second month of the quarter 2 growth rate is known, 89% of the quarterly growth rate of quarter 2 has been determined. Only a large change in growth in the final month of the second quarter will significantly alter quarterly growth (although it helps set the table for growth in the next quarter).
In order to illustrate the difference that can be made by the timing of growth in the first month of quarter 2 relative to that of other months, Figure 3.8 and Figure 3.9 show quarterly sales in a hypothetical industry under two scenarios. In scenario 1, there is 1% growth in every month, with the exception of a 10% increase in June, the final month of quarter 2, when an incentive to purchase was offered to customers. Sales during quarter 1 averaged $101 billion (at annual rates), while sales during quarter 2 averaged $107.2 billion, leaving quarterly growth up 6.1%. In scenario 2, the incentive is offered in April, the first month of quarter 2; there is 1% growth in every other month but April, in which the 10% increase occurs. While sales during quarter 1 were $101 billion (at annual rates) and reached $114.5 billion in the final month of quarter 2 in both scenarios, total sales for quarter 2 were $113.3 billion when the incentive boosted sales in April, and quarterly growth was 12.2%, twice the quarterly growth when the incentive boosted sales in June.
Growth rate relationships: Summary
The same basic principles that have applied to monthly and quarterly, and quarterly and annual average growth rates, apply to a variety of other frequencies. For example, the same dynamic exists between monthly growth rates and annual average growth rates. In the two years being compared, there are 24 monthly growth rates. The growth rate for the first month of year 1 has no impact on the annual growth rate of year 2. Consequently, 23 monthly growth rates play a role in the annual growth rate. The growth rate for the first month of year 2 has the largest impact on annual growth, more than any other individual month. The month's impact on annual growth increases incrementally from the second month in year 1 to the first month of year 2 and then declines each month until the end of year 2.
The relationship between annual average growth rates and the growth between two adjacent decades provides another example. Of the 20 years involved in the calculation, the first year of decade 1 has no impact. The second year of decade 1 has the least impact; the impact then increases incrementally until it reaches its maximum, in the first year of decade 2. The impact declines incrementally until the final year of decade 2. The 1960s and 1970s provide an example. The 1970s were the last decade when average real GDP growth approached the 5.6% rate posted in the 1960s. However, this is explained by strong gains early in the decade: real GDP growth averaged 4.9% from 1970 to 1973 but then slowed to 3.7% over the remainder of the decade. The early years of the 1970s therefore played a large role in determining the decade's growth rate of 4.2%.
In summary, the main principles of growth rates can be applied to any combination of frequencies for which average levels are being compared.
These principles are the following:
- A period (such as a year) is made up of sub-periods (quarters or months). Period 2 is the more recent period, and it is the growth in period 2 that is being calculated. Period 1 is the period that precedes period 2.
- The pattern of growth in both period 1 and period 2 affects the growth rate of period 2.
- There is a hierarchy for which sub-period growth rates have the most impact: growth rates at the turn of the period have the largest impact, while those at the edges have the smallest impact. The first growth rate of period 1 has no impact.
- The sub-period's impact is measured by the percentage of the sub-period's growth rate that is passed through to the period 2 average growth rate. The timing (or placement) of a sub-period determines the size of the impact on the period 2 growth rate, as this shapes the extent to which compounding can occur throughout period 2.
- The specific impact of a sub-period can be calculated by putting its growth rate into the equation and leaving other periods at zero growth. More specifically, it can be calculated by adding in the growth rates one at a time into the equation and then observing the resulting change in the average growth rate for the period (the impact pyramid of series in which large percent changes occur may differ considerably from the 1% quarterly growth rate used in our example).
- This paper has focused on economic indicators, but the dynamic of growth rates can be extrapolated to other types of data.
- Date modified: