4.5 Mesures de la dispersion
4.5.2 Visualiser la boîte à moustaches
Début du texte
La boîte à moustaches, parfois appelée diagramme en boîte ou diagramme de quartiles, est un type de diagramme qui permet de visualiser le résumé en cinq nombres. Elle ne montre pas la distribution avec autant de détails que l’histogramme, mais elle est particulièrement utile pour indiquer si une distribution est asymétrique et s’il y a des valeurs potentiellement extrêmes dans l’ensemble de données. La boîte à moustaches est également idéale pour comparer des distributions, car elle fait apparaître immédiatement le centre, la dispersion et l’étendue.
La figure 4.5.2.1 montre comment on construit la boîte à moustaches à partir du résumé en cinq nombres.
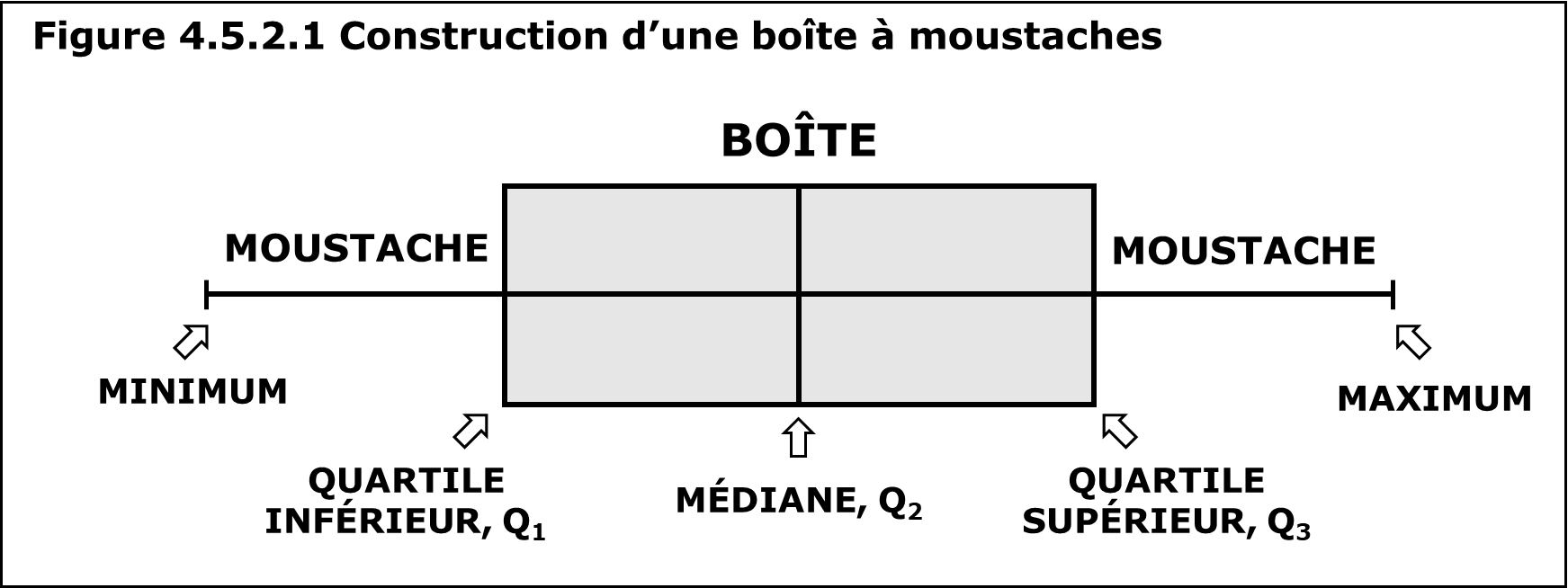
Description de la figure 4.5.2.1
La figure montre la forme d’une boîte à moustaches et la position du minimum, du quartile inférieur, de la médiane, du quartile supérieure et du maximum.
Dans une boîte à moustaches :
- Les côtés gauche et droit de la boîte sont les quartiles inférieur et supérieur. La boîte couvre donc l’intervalle interquartile, là où se situent 50 % des données.
- La ligne verticale qui sépare la boîte en deux représente la médiane. Parfois, la moyenne est également indiquée par un point ou une croix sur la boîte à moustaches.
- Les moustaches sont les deux lignes horizontales à l’extérieur de la boîte qui s’étendent du minimum jusqu’au quartile inférieur (le début de la boîte) et du quartile supérieur (la fin de la boîte) jusqu’au maximum.
- Le diagramme est habituellement accompagné d’un axe qui indique les valeurs (non montré à la figure 4.5.2.1).
- La boîte à moustache peut être présentée horizontalement, comme à la figure 4.5.2.1, ou verticalement.
Une variante de la boîte à moustaches restreint la longueur des moustaches à un maximum d’une fois et demi la valeur de l’écart interquartile. C’est-à-dire que la moustache s’étire jusqu’à la valeur qui est la plus éloignée du centre, mais qui respecte une distance maximale de 1,5 fois l’écart interquartile en partant du quartile inférieur ou du quartile supérieur. Les données qui dépassent cette limite sont indiquées par des points et considérées comme potentiellement extrêmes.
Exemple 1 – Comparaison de trois distributions représentées par des boîtes à moustaches
Les trois boîtes à moustaches du graphique 4.5.2.1 ci-dessous ont été créées à l’aide du logiciel R. Que peut-on affirmer à propos de ces distributions?
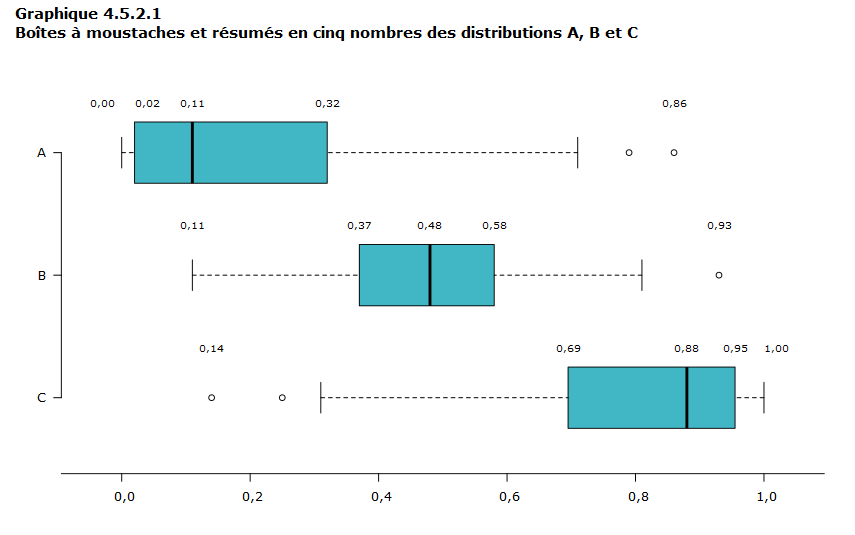
Tableau de données du graphique 4.5.2.1
| Mesure | Distribution A | Distribution B | Distribution C |
|---|---|---|---|
| Minimum | 0,00 | 0,11 | 0,14 |
| Quartile inférieur (Q1) | 0,02 | 0,37 | 0,69 |
| Médiane (Q2) | 0,11 | 0,48 | 0,88 |
| Quartile supérieur (Q3) | 0,32 | 0,58 | 0,95 |
| Maximum | 0,86 | 0,93 | 1,00 |
- Le centre de la distribution A est le plus bas des trois distributions (médiane à 0,11). La distribution est positivement asymétrique, car la portion droite de la boîte et la moustache droite sont plus longues qu’à gauche de la médiane.
- La distribution B est approximativement symétrique, car les deux moitiés de la boîte sont de longueurs sensiblement égales (0,11 du côté gauche et 0,10 du côté droit). C’est la distribution la plus concentrée, car l’écart interquartile est de 0,21, comparativement à 0,30 pour la distribution A et 0,26 pour la distribution C.
- Le centre de la distribution C est le plus élevé des trois distributions (médiane à 0,88). La distribution C est négativement asymétrique, car la portion gauche de la boîte et la moustache gauche sont plus longues que du côté droit.
Les trois distributions incluent des valeurs potentiellement extrêmes. Prenons par exemple la distribution A. L’écart interquartile est de Q3 - Q1 = 0,32 – 0,02 = 0,30. Selon la définition utilisée par la fonction du logiciel R, toute valeur qui dépasse Q3 + 1,5 x (Q3 - Q1) = 0,32 + 1,5 x 0,30 = 0,77 se trouve à l’extérieur de la moustache et est indiquée par un cercle. Il y a deux valeurs potentiellement extrêmes dans la distribution A.
- Date de modification :