4.4 Mesures de la tendance centrale
4.4.2 Calcul de la médiane
Début du texte
La médiane est le point milieu d’un jeu de données, de sorte que 50 % des unités ont une valeur inférieure ou égale à la médiane et 50 % des unités ont une valeur supérieure ou égale. Dans un jeu de données de petite taille, il suffit de compter le nombre de valeurs (n) et de les ordonner en ordre croissant. Si le nombre de valeurs est un nombre impair, il faut lui additionner 1, puis le diviser par 2 pour obtenir le rang qui correspondra à la médiane. Le rang est la position d’une valeur une fois l’ensemble ordonné : la plus petite valeur correspond au rang 1, la seconde plus petite valeur au rang 2, etc.
Exemple 1 – Temps médian au 200 mètres d’un champion de course
Supposons qu’un champion de course effectue une course d’entraînement typique de 200 mètres dans les temps suivants : 26,1 secondes, 25,6 secondes, 25,7 secondes, 25,2 secondes, 25,0 secondes, 27,8 secondes et 24,1 secondes. Comment calcule-t-on le temps médian?
Commençons par classer les valeurs en ordre croissant.
| Rang | Temps (en secondes) |
|---|---|
| 1 | 24,1 |
| 2 | 25,0 |
| 3 | 25,2 |
| 4 | 25,6 |
| 5 | 25,7 |
| 6 | 26,1 |
| 7 | 27,8 |
Il y a n = 7 valeurs, un nombre impair. La médiane correspondra donc à la valeur de rang
(n+1) ÷ 2 = (7 +1) ÷ 2 = 4
Le temps médian est de 25,6 secondes.
Si le nombre de valeurs est un nombre pair, la médiane correspondra à la moyenne des valeurs de rang n ÷ 2 et (n ÷ 2) +1.
Exemple 2 – Temps médian au 200 mètres d’un champion de course (Partie 2)
Maintenant, supposons que le coureur effectue sa huitième course de 200 mètres en 24,7 secondes. Dans ce cas, quelle est la valeur médiane?
| Rang | Temps (en secondes) |
|---|---|
| 1 | 24,1 |
| 2 | 24,7 |
| 3 | 25,0 |
| 4 | 25,2 |
| 5 | 25,6 |
| 6 | 25,7 |
| 7 | 26,1 |
| 8 | 27,8 |
Il y a maintenant n = 8 valeurs, un nombre pair. La médiane correspondra à la moyenne entre la valeur de rang
n ÷ 2 = 8 ÷ 2 = 4
et la valeur de rang
(n ÷ 2) + 1 = (8 ÷ 2) +1 = 5
Le temps médian est donc de (25,2 +25,6) ÷ 2 = 25,4 secondes.
Pour les ensembles de données plus grands, il est possible d’utiliser la distribution de fréquence relative cumulée pour aider à identifier la médiane. La médiane sera la plus petite valeur pour laquelle la fréquence relative cumulée atteint au moins 50 %. Il est toutefois mieux d’utiliser une fonction statistique de base disponible dans un tableur ou un logiciel statistique, car le résultat sera plus fiable. Voyons un exemple.
Exemple 3 – Taille médiane du ménage des élèves de la classe
Supposons que vous demandez aux 30 élèves de votre classe combien de personnes vivent dans leur ménage. Vous résumez les données recueillies dans un tableau de fréquences, dans lequel vous incluez la fréquence relative et la fréquence relative cumulée.
| Taille du ménage | Fréquence (nombre d’élèves) | Fréquence relative (%) | Fréquence cumulée (nombre d’élèves) | Fréquence relative cumulée (%) |
|---|---|---|---|---|
| 2 | 3 | 10,0 | 3 | 10,0 |
| 3 | 4 | 13,3 | 7 | 23,3 |
| 4 | 10 | 33,3 | 17 | 56,7 |
| 5 | 4 | 13,3 | 21 | 70,0 |
| 6 | 2 | 6,7 | 23 | 76,7 |
| 7 | 3 | 10,0 | 26 | 86,7 |
| 8 | 1 | 3,3 | 27 | 90,0 |
| 9 | 2 | 6,7 | 29 | 96,7 |
| 10 | 1 | 3,3 | 30 | 100,0 |
Vous pouvez voir que 10,0 % des élèves (3 élèves) vivent dans un ménage de taille 2, 23,3 % des élèves (7 élèves) vivent dans un ménage de taille 3 ou moins et 56,7 % des élèves (17 élèves) vivent dans un ménage de taille 4 ou moins. La médiane sera égale à 4, car c’est la plus petite valeur pour laquelle la fréquence cumulée dépasse 50 %. Ceci est encore plus évident si on visualise la fréquence relative cumulée grâce à un graphique à barres comme le graphique 4.4.2.1 ci-dessous. La ligne pointillée y indique la fréquence relative cumulée de 50 %.
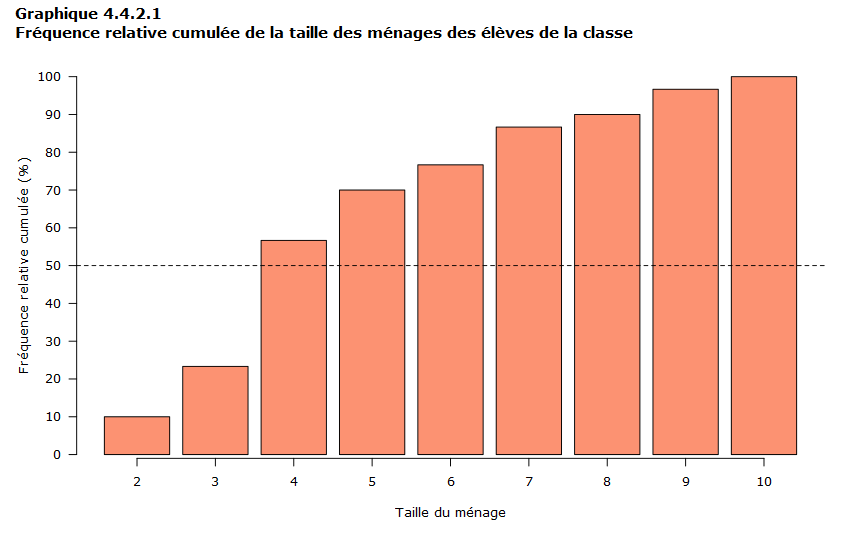
Tableau de données du graphique 4.4.2.1
| Taille du ménage | Fréquence relative cumulée (%) |
|---|---|
| 2 | 10,0 |
| 3 | 23,3 |
| 4 | 56,7 |
| 5 | 70,0 |
| 6 | 76,7 |
| 7 | 86,7 |
| 8 | 90,0 |
| 9 | 96,7 |
| 10 | 100,0 |
La moyenne, quant à elle, est obtenue en divisant le nombre total de personne dans les ménages des élèves de la classe :
2 × 3 + 3 × 4 + 4 × 10 + 5 × 4 + 6 × 2 + 7 × 3 + 8 × 1 + 9 × 2 + 10 × 1 = 147
par le nombre d’élèves (30). Elle est donc de 147 ÷ 30 = 4,9 personnes par ménage.
Dans cet exemple, la médiane (4) est un peu plus petite que la moyenne (4,9).
L’avantage d’utiliser la médiane plutôt que la moyenne est qu’elle est plus robuste aux valeurs extrêmes qui pourraient surgir à l’une des extrémités de la distribution. Il est donc important de vérifier si les données comptent des valeurs extrêmes avant de choisir quelle mesure de tendance centrale doit être utilisée. Ceci sera illustré par l’exemple ci-dessous.
Exemple 4 – Taille médiane du ménage des élèves de la classe (Partie 2)
Un nouvel élève est récemment inscrit dans votre classe. Vous décidez de vous renseigner auprès de lui sur la taille de son ménage afin de mettre vos résultats à jour. Il vous répond qu’il habite dans une très grande maison multigénérationnelle, qui compte 18 résidents !
La valeur de la moyenne après la mise à jour sera de (147 + 18) ÷ 31 = 5,3 personnes par ménage. Cet élève à lui seul a fait augmenter la moyenne de 0,4 personnes par ménage (5,3 - 4,9 = 0,4). Quant à la médiane, elle est restée inchangée. En effet, la fréquence relative cumulée pour la valeur 3 est de 7 ÷ 31 = 22,6 % et celle pour la valeur 4 de 17 ÷ 31 = 54,8 %. La valeur 4 est encore la plus petite valeur à atteindre une fréquence relative cumulée d’au moins 50 %.
- Date de modification :